Электрическое сопротивление — физическая величина, которая указывает, какое препятствие создается току при его прохождении по проводнику. Единицами измерения служат Омы, в честь Георга Ома. В собственном законе он вывел формулу для нахождения сопротивления, которая приведена ниже.
Разглядим сопротивление проводников на примере металлов. Металлы имеют внутреннее строение в виде кристаллической решетки. Эта решетка имеет строгую упорядоченность, а её узлами являются положительно заряженные ионы. Носителями заряда в металле выступают “свободные” электроны, которые не принадлежат определенному атому, а беспорядочно передвигаются между узлами решетки. Из квантовой физики понятно, что движение электронов в металле это распространение электромагнитной волны в жестком теле. Другими словами электрон в проводнике движется со скоростью света (фактически), и подтверждено, что он проявляет характеристики не только лишь как частичка, но к тому же как волна. А сопротивление металла появляется в итоге рассеяния электромагнитных волн (другими словами электронов) на термических колебаниях решетки и её недостатках. При столкновении электронов с узлами кристаллической решетки часть энергии передается узлам, вследствие чего выделяется энергия. Эту энергию можно вычислить при неизменном токе, благодаря закону Джоуля-Ленца – Q=I 2 Rt. Видите ли чем больше сопротивление, тем больше энергии выделяется.
Удельное сопротивление
Существует такое принципиальное понятие как удельное сопротивление, это тоже самое сопротивление, исключительно в единице длины. У каждого металла оно свое, к примеру у меди оно равно 0,0175 Ом*мм2/м, у алюминия 0,0271 Ом*мм2/м . Это означает, брусок из меди длиной 1 м и площадью поперечного сечения 1 мм2 будет иметь сопротивление 0,0175 Ом, а таковой же брусок, но из алюминия будет иметь сопротивление 0,0271 Ом. Выходит что электропроводность меди выше чем у алюминия. У каждого металла удельное сопротивление свое, а высчитать сопротивление всего проводника можно по формуле
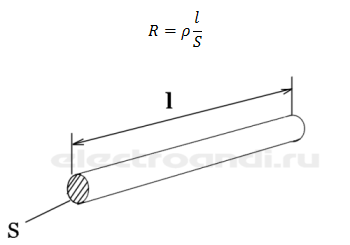
где p – удельное сопротивление металла, l – длина проводника, s – площадь поперечного сечения.
Значения удельных сопротивлений приведены в таблице удельных сопротивлений металлов (20°C)
Не считая удельного сопротивления в таблице есть значения ТКС, об этом коэффициенте чуток позднее.
Зависимость удельного сопротивления от деформаций
При холодной обработке металлов давлением, металл испытывает пластическую деформацию. При пластической деформации кристаллическая решетка искажается, количество изъянов становится больше. С повышением изъянов кристаллической решетки, сопротивление течению электронов по проводнику вырастает, поэтому, удельное сопротивление металла возрастает. Например, проволоку изготавливают способом протяжки, это означает, что металл испытывает пластическую деформацию, в итоге чего, удельное сопротивление вырастает. На практике для уменьшения сопротивления используют рекристаллизационный отжиг, это непростой технологический процесс, после которого кристаллическая решетка вроде бы, “расправляется” и количество изъянов миниатюризируется, поэтому, и сопротивление металла тоже.
При растяжении либо сжатии, металл испытывает упругую деформацию. При упругой деформации вызванной растяжением, амплитуды термических колебаний узлов кристаллической решетки растут, поэтому, электроны испытывают огромные затруднения, и в связи с этим, возрастает удельное сопротивление. При упругой деформации вызванной сжатием, амплитуды термических колебаний узлов уменьшаются, поэтому, электронам проще двигаться, и удельное сопротивление миниатюризируется.
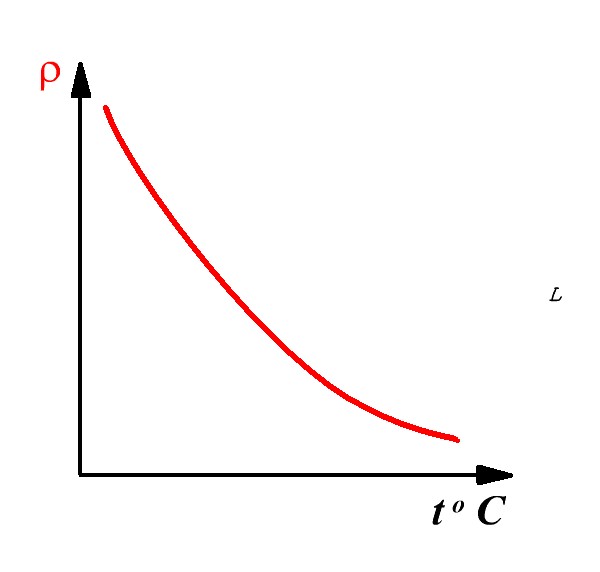
Воздействие температуры на удельное сопротивление
Как мы уже узнали выше, предпосылкой сопротивления в металле являются узлы кристаллической решетки и их колебания. Итак вот, при увеличении температуры, термические колебания узлов растут, а означает, удельное сопротивление также возрастает. Существует такая величина как температурный коэффициент сопротивления (ТКС), который указывает как возрастает, либо миниатюризируется удельное сопротивление металла при нагреве либо охлаждении. К примеру, температурный коэффициент меди при 20 градусах по цельсию равен 4.1 · 10 − 3 1/градус. Это значит что при нагреве, например, медной проволоки на 1 градус цельсия, её удельное сопротивление возрастет на 4.1 · 10 − 3 Ом. Удельное сопротивление при изменении температуры можно вычислить по формуле
где r это удельное сопротивление после нагрева, r0 – удельное сопротивление до нагрева, a – температурный коэффициент сопротивления, t2 – температура до нагрева, t1 — температура после нагрева.
Подставив наши значения, мы получим: r=0,0175*(1+0.0041*(154-20))=0,0271 Ом*мм 2 /м. Видите ли наш брусок из меди длиной 1 м и площадью поперечного сечения 1 мм 2 , после нагрева до 154 градусов, имел бы сопротивление, как у того же бруска, только из алюминия и при температуре равной 20 градусов цельсия.
Свойство конфигурации сопротивления при изменении температуры, применяется в указателях температуры сопротивления. Эти приборы могут определять температуру основываясь на показаниях сопротивления. У термометров сопротивления высочайшая точность измерений, но малые спектры температур.
На практике, характеристики проводников препятствовать прохождению тока применяются очень обширно. Примером может служить лампа накаливания, где нить из вольфрама, греется за счет высокого сопротивления металла, большой длины и узенького сечения. Либо хоть какой нагревательный устройство, где спираль разогревается благодаря высочайшему сопротивлению. В электротехнике, элемент основным свойством которого является сопротивление, именуется – резистор. Резистор применяется фактически в хоть какой электрической схеме.
Удельное сопротивление
Вещества и материалы, способные проводить электрический ток, именуют проводниками. Другие относят к диэлектрикам. Но незапятнанных диэлектриков не бывает, они все тоже проводят ток, но его величина очень мала.
Но и проводники по-разному проводят ток. Согласно формуле Георга Ома, ток, протекающий через проводник, линейно пропорционален величине приложенного к нему напряжения, и назад пропорционален величине, именуемой сопротивлением.
Единицу измерения сопротивления окрестили Омом в честь ученого, открывшего эту зависимость. Но выяснилось, что проводники, сделанные из различных материалов и имеющие однообразные геометрические размеры, владеют различным электрическим сопротивлением. Дабы найти сопротивление проводника известного длины и сечения, ввели понятие удельного сопротивления — коэффициента, зависящего от материала.
В конечном итоге сопротивление проводника известной длины и сечения будет равно
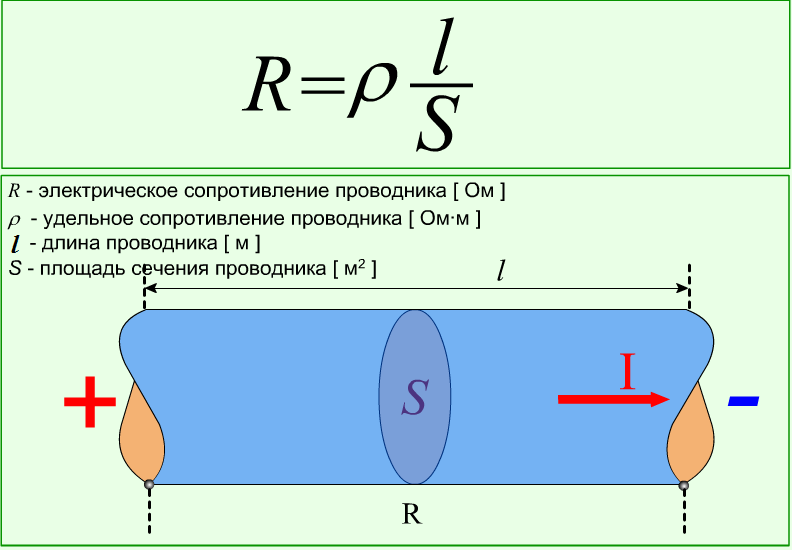
Определение сопротивления проводника при помощи его удельного сопротивления
Удельное сопротивление применимо не только лишь к жестким материалам, но и к жидкостям. Но его величина зависит к тому же от примесей либо других компонент в начальном материале. Незапятнанная вода не проводит электрический ток, являясь диэлектриком. Но в природе дистиллированной воды не бывает, в ней всегда встречаются соли, бактерии и другие примеси. Этот коктейль – проводник электрического тока, владеющий удельным сопротивлением.
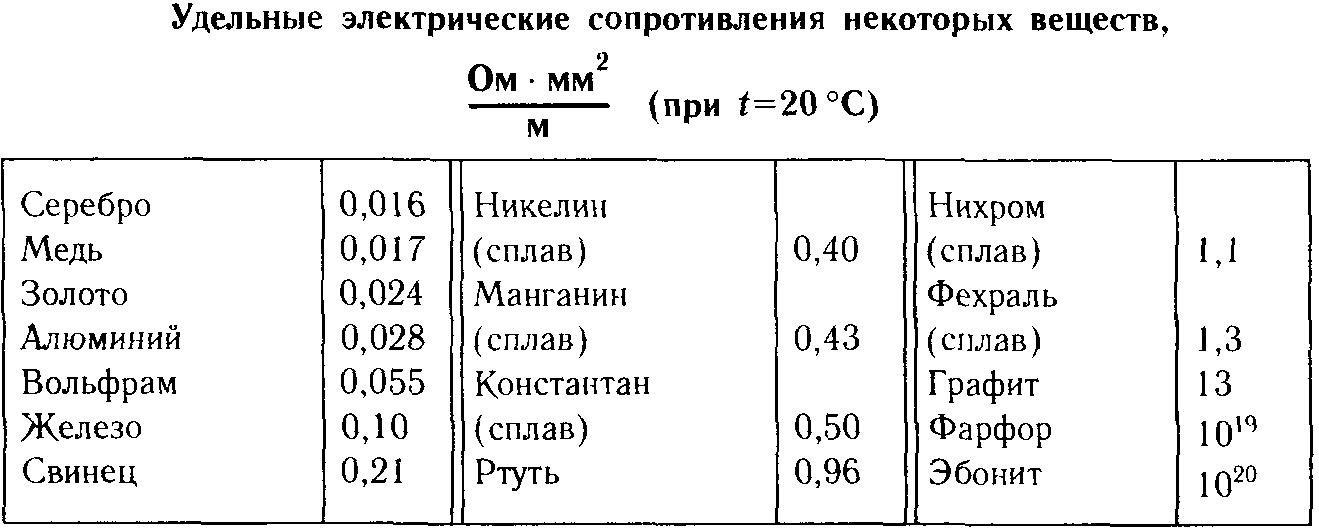
Удельные сопротивления некоторых материалов
Внедряя в металлы разные добавки, получают новые материалы – сплавы, удельное сопротивление которых отличается от того, что было у начального материала, даже если добавка в него в процентном соотношении малозначительна.
Зависимость удельного сопротивления от температуры
Удельные сопротивления материалов приводятся в справочниках для температуры, близкой к комнатной (20 °С). При увеличении температуры возрастает сопротивление материала. Почему так происходит?
Электрического тока снутри материала проводят свободные электроны. Они под действием электрического поля отрываются от собственных атомов и передвигаются между ними в направлении, данным этим полем. Атомы вещества образуют кристаллическую решетку, между узлами которой и движется поток электронов, именуемый еще «электронным газом». Под действием температуры узлы решетки (атомы) колеблются. Сами электроны тоже движутся не по прямой, а по запутанной линии движения. При всем этом они нередко сталкиваются с атомами, меняя траекторию перемещения. В некоторые моменты времени электроны могут двигаться в сторону, оборотную направлению электрического тока.
С повышением температуры амплитуда колебаний атомов возрастает. Соударение электронов с ними происходит почаще, движение потока электронов замедляется. На физическом уровне это выражается в увеличении удельного сопротивления.
Примером применения зависимости удельного сопротивления от температуры служит работа лампы накаливания. Вольфрамовая спираль, из которой изготовлена нить накала, в момент включения имеет маленькое удельное сопротивление. Бросок тока в момент включения стремительно ее разогревает, удельное сопротивление возрастает, а ток – миниатюризируется, становясь номинальным.
Тот же процесс происходит и с нагревательными элементами из нихрома. Потому и высчитать их рабочий режим, определив длину нихромовой проволоки известного сечения для сотворения требуемого сопротивления, не выходит. Для расчетов необходимо удельное сопротивление нагретой проволоки, а в справочниках приведены значения для комнатной температуры. Потому итоговую длину спирали из нихрома подгоняют экспериментально. Расчетами же определяют примерную длину, а при подгонке понемногу укорачивают нить участок за участком.
Температурный коэффициент сопротивления
Но не во всех устройствах наличие зависимости удельного сопротивления проводников от температуры приносит пользу. В измерительной технике изменение сопротивления частей схемы приводит к возникновению погрешности.
Для количественного определения зависимости сопротивления материала от температуры введено понятие температурного коэффициента сопротивления (ТКС). Он указывает, как меняется сопротивление материала при изменении температуры на 1°С.
Для производства электронных компонент – резисторов, применяемых в схемах измерительной аппаратуры, используются материалы с низким ТКС. Они стоят дороже, но зато характеристики устройства не меняются в широком спектре температур окружающей среды.
Но характеристики материалов с высочайшим ТКС тоже применяются. Работа некоторых датчиков температуры базирована на изменении сопротивления материала, из которого сделан измерительный элемент. Для этого необходимо поддерживать размеренное напряжение питания и определять ток, проходящий через элемент. Откалибровав шкалу устройства, измеряющего ток, по примерному указателю температуры, получают электронный измеритель температуры. Этот принцип применяется не только лишь для измерений, но и для датчиков перегрева. Отключающих устройство при появлении ненормальных режимов работы, приводящих к перегреву обмоток трансформаторов либо силовых полупроводниковых частей.
Применяются в электротехнике и элементы, изменяющие свое сопротивление не от температуры окружающей среды, а от тока через них – терморезисторы. Пример их применения – системы размагничивания электронно-лучевых трубок телевизоров и мониторов. При подаче напряжения сопротивление резистора мало, ток через него проходит в катушку размагничивания. Но тот же ток нагревает материал терморезистора. Его сопротивление возрастает, понижая ток и напряжение на катушке. И так – до полного его исчезновения. В конечном итоге на катушку подается синусоидальное напряжение с плавненько уменьшающейся амплитудой, создающее в ее пространстве такое же магнитное поле. Итог – к моменту разогрева нити накала трубки она уже размагничена. А схема управления остается в запертом состоянии, пока аппарат не выключат. Тогда терморезисторы остынут и будут готовы к работе опять.
Явление сверхпроводимости
А что будет, если температуру материала уменьшать? Удельное сопротивление будет уменьшаться. Есть предел, до которого миниатюризируется температура, именуемый абсолютным нулем. Это —273°С. Ниже этого предела температур не бывает. При всем этом значении удельное сопротивление любого проводника равно нулю.
При абсолютном нуле атомы кристаллической решетки перестают колебаться. В конечном итоге электронное скопление движется между узлами решетки, не соударяясь с ними. Сопротивление материала становится равным нулю, что открывает способности для получения нескончаемо огромных токов в проводниках маленьких сечений.
Явление сверхпроводимости открывает новые горизонты для развития электротехники. Но еще пока есть трудности, связанные с получением в бытовых критериях сверхнизких температур, нужных для сотворения этого эффекта. Когда задачи будут решены, электротехника перейдет на новый уровень развития.
Примеры применения значений удельного сопротивления при расчетах
Мы уже познакомились с принципами расчета длины нихромовой проволоки для производства нагревательного элемента. Но есть и другие ситуации, когда нужны познания удельных сопротивлений материалов.
Для расчета контуров заземляющих устройств применяются коэффициенты, надлежащие типовым грунтам. Если же тип грунта в месте устройства контура заземления неизвестен, то для правильных расчетов за ранее определяют его удельное сопротивление. Так результаты расчетов оказываются поточнее, что исключает подгонку характеристик контура при изготовлении: добавление числа электродов, приводящее к повышению геометрических размеров заземляющего устройства.
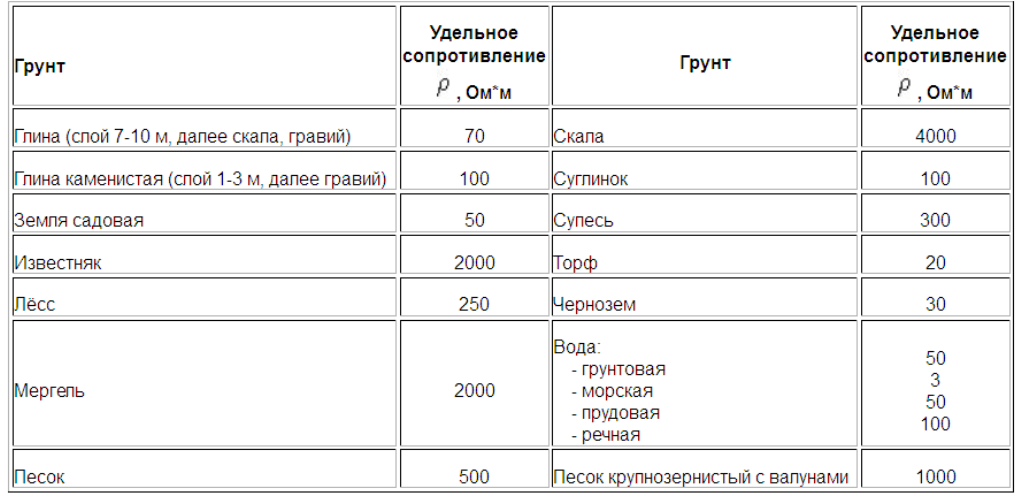
Удельные сопротивления грунтов
Удельное сопротивление материалов, из которых сделаны кабельные полосы и шинопроводы, применяется для расчетов их активного сопротивления. В предстоящем при номинальном токе нагрузки с его помощью рассчитывается величина напряжения в конце полосы. Если его величина окажется недостаточной, то заранее наращивают сечения токопроводов.