Зависимость сопротивления проводника от температуры

Удельное сопротивление, а поэтому, и сопротивление металлов, находится в зависимости от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника разъясняется тем, что

1. увеличивается интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры;
2. меняется их концентрация при нагревании проводника.

Опыт указывает, что при не очень больших и не очень низких температурах зависимости удельного сопротивления и сопротивления проводника от температуры выражаются формулами:

\(~\rho_t = \rho_0 (1 + \alpha t) ,\) \(~R_t = R_0 (1 + \alpha t) ,\)

где ρ0, ρt — удельные сопротивления вещества проводника соответственно при 0 °С и t °C; R0, Rt — сопротивления проводника при 0 °С и t °С, α — температурный коэффициент сопротивления: измеряемый в СИ в Кельвинах в минус первой степени (К -1 ). Для железных проводников эти формулы применимы начиная с температуры 140 К и выше.

Температурный коэффициент сопротивления вещества охарактеризовывает зависимость конфигурации сопротивления при нагревании от рода вещества. Он численно равен относительному изменению сопротивления (удельного сопротивления) проводника при нагревании на 1 К.

где \(~\mathcal h \alpha \mathcal i\) — среднее значение температурного коэффициента сопротивления в интервале ΔΤ.

Для всех железных проводников α > 0 и слабо меняется с конфигурацией температуры. У незапятнанных металлов α = 1/273 К -1 . У металлов концентрация свободных носителей зарядов (электронов) n = const и повышение ρ получается благодаря росту интенсивности рассеивания свободных электронов на ионах кристаллической решетки.

Для смесей электролитов α < 0, к примеру, для 10%-ного раствора поваренной соли α = -0,02 К -1 . Сопротивление электролитов с ростом температуры миниатюризируется, так как повышение числа свободных ионов из-за диссоциации молекул превосходит рост рассеивания ионов при столкновениях с молекулами растворителя.

Формулы зависимости ρ и R от температуры для электролитов подобны приведенным выше формулам для железных проводников. Стоит отметить, что эта линейная зависимость сохраняется только в маленьком спектре конфигурации температур, в каком α = const. При огромных же интервалах конфигурации температур зависимость сопротивления электролитов от температуры становится нелинейной.

Графически зависимости сопротивления железных проводников и электролитов от температуры изображены на рисунках 1, а, б.

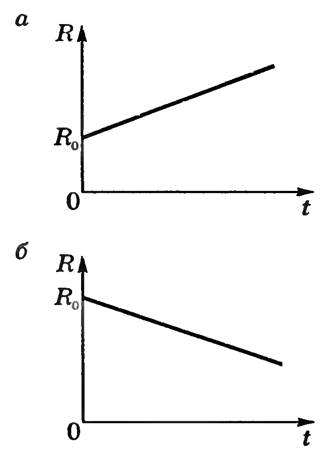
При очень низких температурах, близких к абсолютному нулю (-273 °С), сопротивление многих металлов скачком падает до нуля. Это явление получило название сверхпроводимости. Металл перебегает в сверхпроводящее состояние.

Зависимость сопротивления металлов от температуры применяют в указателях температуры сопротивления. Обычно в качестве термометрического тела такового указателя температуры берут платиновую проволоку, зависимость сопротивления которой от температуры довольно исследована.

Об конфигурациях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие указатели температуры позволяют определять очень низкие и очень высочайшие температуры, когда обыденные жидкостные указатели температуры неприменимы.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Испытания: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 256-257.

Зависимость сопротивления проводника от температуры

Говоря о законе Ома (§ 1.7), мы подчеркивали требование неизменности таких физических критерий, как температура и давление. Дело в том, что обычно сопротивление проводников находится в зависимости от температуры:

сопротивление железных проводов возрастает с нагреванием.

Для медных проводов повышение температуры на каждые 2,5 °С вызывает повышение сопротивления примерно на 1 % (на одну сотую их начального сопротивления), либо сопротивление возрастает на 0,4 % при увеличении температуры на 1 °С. Те значения удельных сопротивлений, которые были приведены выше, соответствуют темйературе 20 °С.

Пример 1. Покажем, как можно подсчитать удельное сопротивление при изменении температуры.

Пусть, к примеру, нужна найти удельное сопротивление меди при температуре 45 °.

Мы знаем, что при 20 °С оно было равно 0,0178 Ом на 1м длины при сечении 1 мм2. Мы знаем, что каждые 2,5 ° оно растет на 1 %, т. е. на

Новенькая температура превосходит 20° С на 25° С.

Означает, разыскиваемое удельное сопротивление на 10 % больше, чем 0,0178: удельное сопротивление при 45° равно Ом на 1 м при сечении 1 мм2.

Зависимостью сопротивления от температуры нередко пользуются для определения температуры медных проводов в электрических машинах.

Этой же зависимостью сопротивления от температуры пользуются для устройства электрических термометров, основанных на измерении сопротивления кусочка проволоки (нередко намотанного в форме спирали), размещенного в том помещении, температуру которого желают найти.

При таком измерении температуры просто сосредоточить в одном месте наблюдение за температурой различных частей помещения (к примеру, в холодильниках) либо различных частей промышленных установок.

При всем этом можно воспользоваться единственным стрелочным измерительным устройством, переводя переключатель в различные положения: при каждом новеньком положении для измерения врубаются проволочные спирали, находящиеся, к примеру, на различных этажах холодильника.

Пример 2. Сопротивление обмотки электрической машины при 20 ° С было равно 60 Ом. После часовой работы машины сопротивление обмотки возросло до 69,6 Ом. Найти, как нагрелась обмотка, если при повышении температуры на каждые 10 ° С сопротивление возрастает на 4 %. ,

Сначала ищем, на сколько процентов возросло сопротивление:

Сейчас просто находим, что температура возросла на 40° С, т. е. стала равной 20+40 = 60° С.

Естественно сейчас должен появиться вопрос: не изменяется ли сопротивление электрических ламп, когда в них накаляется нить? Ответ: да, естественно, сопротивление нити холодной лампы меньше, чем сопротивление в рабочем состоянии. К этому и относилось наше примечание, изготовленное в § 1.7.

Заметим только-только очень нередко нелинейность свойства разъясняется чисто электрическими явлениями. Так обстоит дело в случае варистора, черта которого приведена на рис. 1.14.

В ряде измерительных устройств и в специальной аппаратуре нередко нужна, дабы их сопротивление не изменялось с температурой. Для таких изделий разработаны сплавы, сопротивление которых фактически не находится в зависимости от температуры.

Из таких сплавов в большинстве случаев применяются манганин и константан.

Многие проводники приметно изменяют свое сопротивление при их растяжении либо сжатии. Это свойство проводников тоже отыскало принципиальное техническое использование: в текущее время нередко по изменению электрического сопротивления специально сделанных частей судят о давлениях и малых перемещениях, возникающих, к примеру, при нагрузках балок, рельсов, частей машины и т. п.

Зависимость сопротивления проводника от температуры.

Если пропустить ток от аккума через железную спираль, то амперметр покажет уменьшение силы тока. Это значит, что с сопротивлением температуры сопротивление проводника изменяется.

Если при температуре, равной 0С, сопротивление проводника равно R0, а при температуре t оно равно R, то относительное изменение сопротивления, как указывает опыт, прямо пропорционально изменению температуры t:

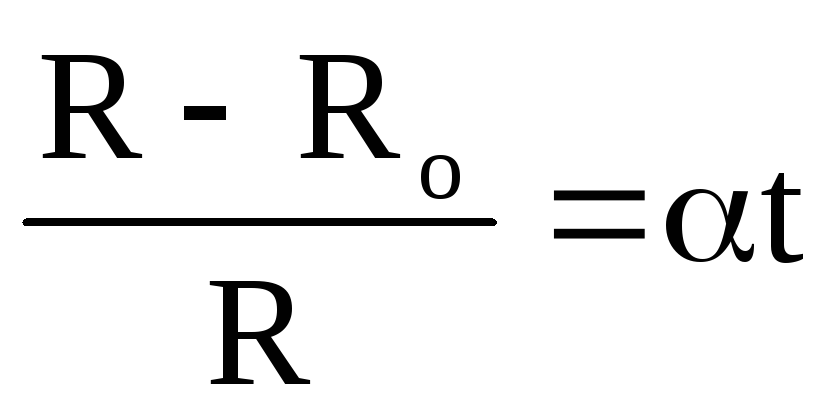
(1)

Коэффициент именуетсятемпературным коэффициентом сопротивления. Он охарактеризовывает зависимость сопротивления вещества от температуры.

Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при повышении температура на 1 К.

Для всех металлов >0 и некординально изменяется с конфигурацией температуры. У смесей электролитов сопротивление с ростом температуры не миниатюризируется, а возрастает. Для них<0.

При нагревании проводника его геометрические размеры изменяются некординально. Сопротивление проводника изменяется в главном за счет конфигурации его удельного сопротивления. Можно отыскать зависимость этого удельного сопротивления от температуры, если в формулу (1) подставить значения

и :

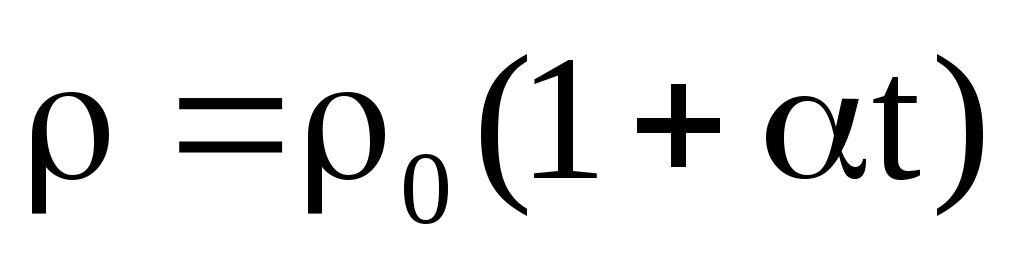
Так как не много изменяется при изменении температуры, то можно считать, что удельное сопротивление проводника линейно находится в зависимости от температуры.

С приближением температуры к абсолютному нулю удельное сопротивление монокристаллов становится очень малым. Данный факт свидетельствует о том, что в безупречной кристаллической решетке металла электроны передвигаются под действием электрического поля, не взаимодействуя с ионами решетки. Электроны ведут взаимодействие только с ионами, не находящимися в узлах кристаллической решетки.

При повышении температуры растет число изъянов кристаллической решетки из-за термических колебаний ионов, – и это приводит к возрастанию удельного сопротивления кристалла.

Сверхпроводимость

В 1911 г. нидерландский ученый Камерлинг-Оннес нашел, что при снижении температуры ртути до 4,1 К ее удельное сопротивление скачком миниатюризируется до нуля. Явление уменьшения удельного сопротивления до нуля при температуре, хорошей от абсолютного нуля, именуется сверхпроводимостью. Материалы, обнаруживающие способность перебегать при некоторых температурах, хороших от абсолютного нуля, в сверхпроводящее состояние, именуются сверхпроводниками.

Прохождение тока в сверхпроводнике происходит без утрат энергии, потому в один прекрасный момент возбужденный в сверхпроводящем кольце электрический ток может существовать неограниченно длительно без конфигурации.

Сверхпроводящие вещества уже применяются в электромагнитах. Но получить сколь угодно сильное магнитное поле при помощи сверхпроводящего магнита нельзя, т. к. очень сильное магнитное поле разрушает сверхпроводящее состояние. Потому для каждого проводника в сверхпроводящем состоянии существует критичное значение силы тока, затмить которое, не нарушая сверхпроводящего состояния, нельзя.

Разъяснение сверхпроводимости может быть лишь на базе квантовой теории. Оно было входные данные только в 1957 г.

В 1986 г. была открыта высокотемпературная сверхпроводимость керамик – соединений лантана, бария, меди и кислорода. Сверхпроводимость таких керамик сохраняется до температур около 100 К.