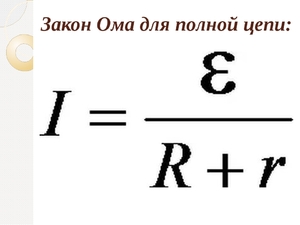Привет, Хабр! С недавнешнего времени я стал думать об актуальности статей и увидел, что на Хабре нет ни одной обзорной статьи про магнитные цепи. Как так!? Ведь это. а что же все-таки это такое?
Вправду, наверное даже самые отстраненные от инженерного дела люди имеют представление о том, что такое электрические цепи, но может быть, что про магнитные цепи не слышали совсем. Каждый школьник когда-то в учебнике физики следил различные схемы и формулы, описывающие законы Ома. Но магнитные цепи в рамки школьного курса не входят.
Я решил написать данную статью, дабы показать, как изумителен мир физики и заинтриговать школьников в её исследовании. В данной статье, совершенно точно, для полноты вещей будут и выводы формул и внедрение некоторых математических операций, которые могут быть известны не многим, но такие моменты я постараюсь сгладить. Приступим!
Что необходимо вспомнить?
Для более ясного понятия сей статьи, хорошо бы вспомнить главные свойства самого магнитного поля: вектор магнитной индукции, вектор напряженности, поток вектора магнитной индукции — также необходимо вспомнить малость про магнитные вещества, а конкретно про ферромагнетики.
Полагается, что для вас известен обобщенный закон Ома и помнится, что такое ток, напряжение и сопротивление. Если нет, то очень советую обратиться к посторонним ресурсам, дабы иметь хотя бы общее представление о том, что последует дальше. Очень советую учебник И.Е. Иродова «Электромагнетизм» .
Использование магнитных цепей
Магнитные цепи находят очень огромное поле использования, а конкретно, они применяются для надежного пропускания магнитного потока по специальному проводнику с наименьшими либо, в некоторых случаях, определенными потерями. В электротехнической индустрии обширно применяется обоюдная зависимость магнитной и электрической энергий, переход из 1-го состояния в другое. На схожем принципе работают, к примеру, трансформаторы, различные электродвигатели, генераторы и другие устройства.
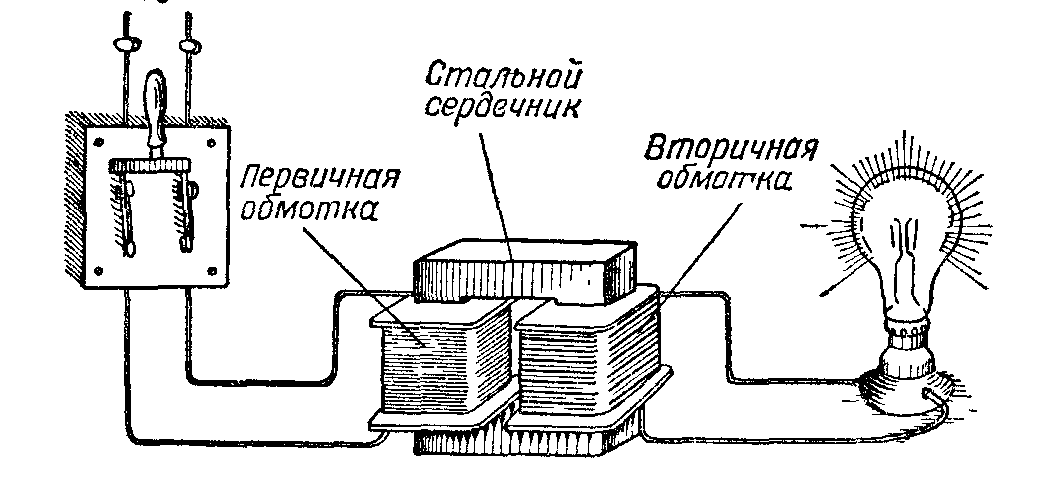
Естественно, можно длительное время гласить об устройствах, различных типах магнитопроводов (про которые пойдет речь дальше), но наша первичная цель — разглядеть выводы главных черт магнитных цепей. Продолжаем!
Как устроены магнитные цепи?
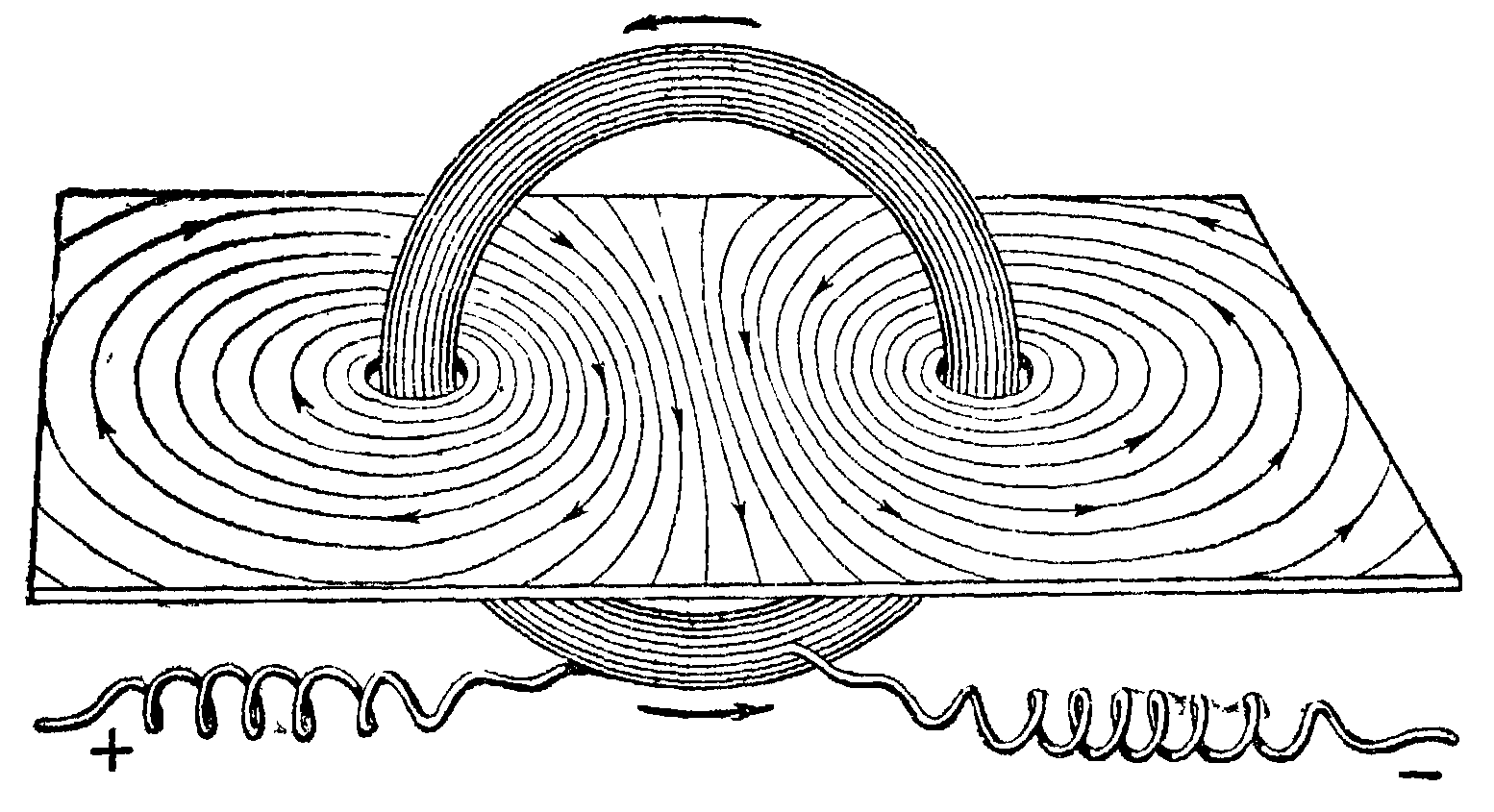
Магнитную цепь, по сути, не так трудно представить, как может показаться человеку, который о них в первый раз слышит. Обычно магнитные цепи представляют из себя некоторые фигуры из ферромагнитного сердечника с источником либо несколькими источниками ПОтока. Пожалуй, один из самых обычных примеров с одним источником, который можно взять на вооружение, проиллюстрирован ниже:
Перед продолжением обусловимся, что посреди электротехников сердечник именуют магнитопроводом. Часть магнитопровода, на которой отсутствуют обмотки и которая служит для замыкания магнитной цепи, именуется «ярмо».
Начнем с тороидального сердечника. Таковой тороидальный сердечник может служить формой для катушки, как бы удивительно это не звучало. Но что за катушка? Ну, 1-ое что идёт в голову — провод, образующий витки. Отлично, но какого его назначение? Вернемся к электрическим цепям и вспомним, что есть источники тока / напряжения, так именуемые активные элементы. Итак вот, в магнитных цепях роль источника делают катушки с током, навороченные на основной элемент магнитной цепи — ферромагнитный магнитопровод.
Вспомним сейчас про ферромагнитные материалы. Почему конкретно они? Дело в том, что благодаря высочайшему значению магнитной проницаемости, что говорит о неплохой намагниченности ферромагнетика, силовые полосы магнитного поля фактически не выходят за границы сердечника, или не выходят совсем. Но это будет справедливо только тогда, когда наш сердечник замкнутый, или имеет маленькие зазоры. Другими словами, ферромагнетики владеют сильно выраженными магнитными качествами, когда как у парамагнетиков и диамагнетиков они существенно слабее, что можно следить на следующем графике зависимости намагниченности от напряженности магнитного поля:
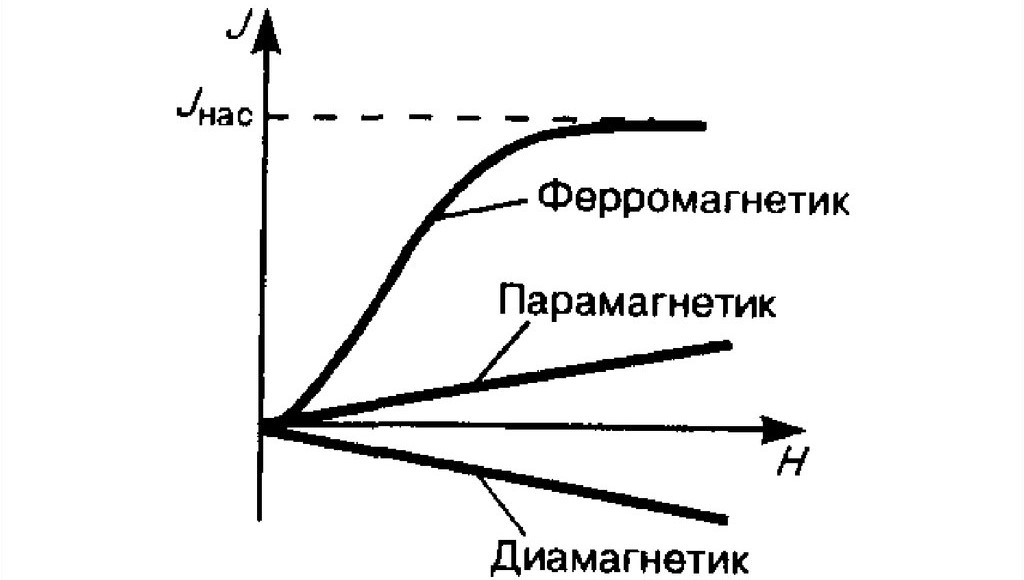
Вещества, которые входят в конструкцию магнитопровода, могут владеть не только лишь сильномагнитными качествами, но также и слабомагнитными. Но мы рассматриваем сердечник из ферромагнитного материала.
Ещё из школьного курса мы представляем для себя картину с линиями магнитной индукции соленоида, мы можем зрительно представить его поле и осознаем, что концентрация силовых линий, их насыщенность, большая в центре рассматриваемого соленоида. Здесь очень принципиально вспомнить правило буравчика, дабы верно указать направление силовых линий.
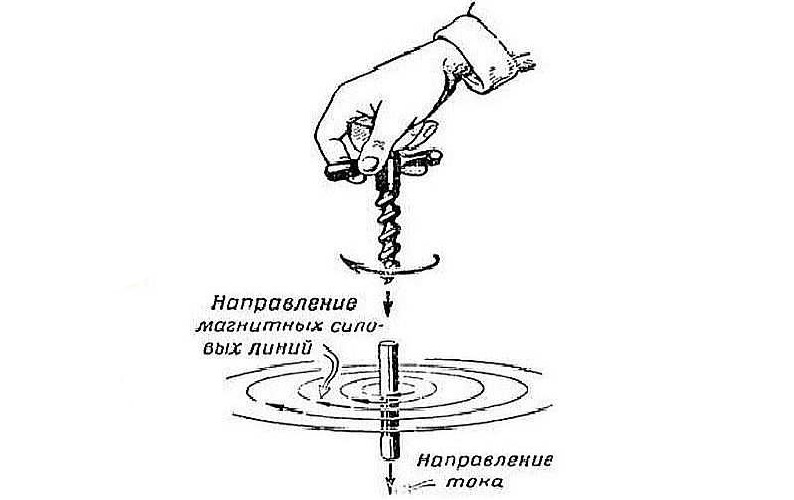
Отсюда становится понятно, что катушки-источники порождают магнитное поле, а поэтому и поток линий магнитной индукции. Такие полосы будут циркулировать по нашему сердечнику, как будто повторяя его форму. Вот поэтому нам принципиально условие замкнутости сердечника и материал, из которого он изготовлен. Положим, что наш воображаемый сердечник замкнут. Из этого следует, что и силовые полосы замкнуты, а поэтому осуществляется аксиома Гаусса для магнитного поля, которая говорит: поток линий магнитной индукции через замкнутую поверхность равен нулю. Стоит учитывать, что поток приспосабливается под площадь сечения.*
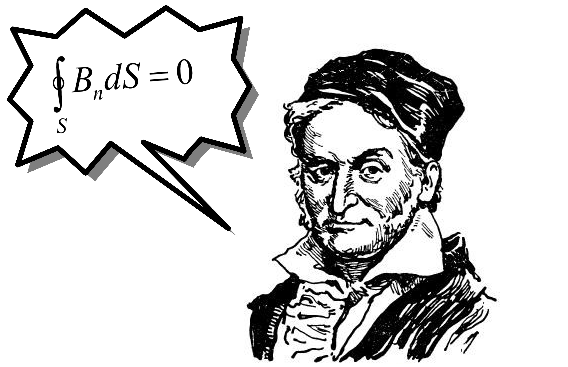
Ну и в конечном счете ферромагнитный сердечник поток куда-то передает! Аналогичным образом замкнутый проводник позволяет передать электрический ток.
Отлично! Мы разобрались с тем, что такое магнитные цепи и даже вспомнили про аксиому Гаусса и ферромагнетики. Сейчас побеседуем о том, какие следствия вытекают из аксиомы Гаусса и способности пренебрежения полем вне сердечника и в зазорах.
1] Магнитные потоки Ф1 и Ф2 через произвольные сечения будут равны между собой.
2] В узле (разветвлении) сердечника алгебраическая сумма потоков (с учетом их направлений) будет равна нулю. Мне одному это что-то припоминает?
Другими словами мы совсем определили, что замкнутая (либо практически замкнутая) система из ферромагнитных сердечников может рассматриваться как проводящая цепь. В нашем случае — магнитная.
Расчет магнитных цепей
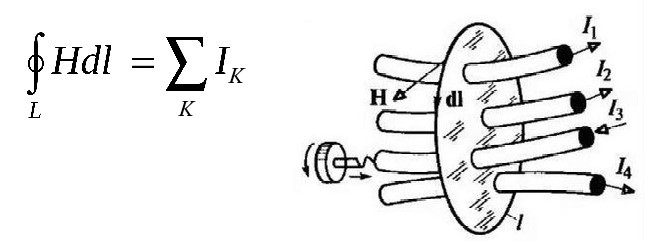
Сейчас внимание. Мы можем провести прямую аналогию и рассматривать магнитный поток в цепи, как характеристику электрической цепи — силу тока. Рассмотренное 2-ое следствие значит, что для магнитной цепи, также как и для электрической, справедливо 1-ое правило Кирхгофа. Отсюда можно лаконически перейти к закону полного тока, который в пределах традиционного магнетизма будет смотреться следующим образом (приготовьтесь, мало арифметики):
Криволинейный интеграл по замкнутому контуру от напряженности магнитного поля будет равен алгебраической сумме токов, сцепленных (окруженных) данным контуром.
Также мы помним, что напряженность магнитного поля связана с магнитным потоком следующим образом:
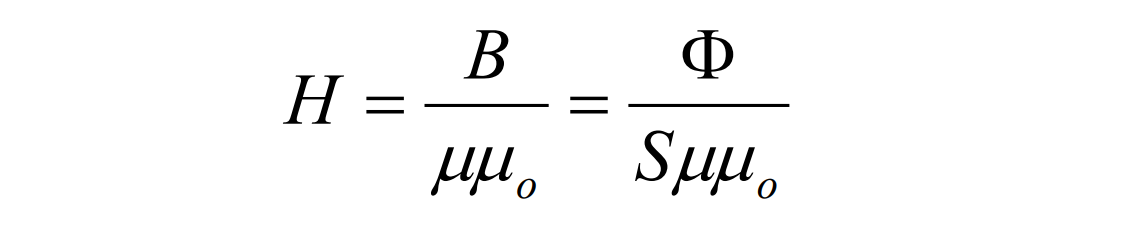
Руководствуясь приведенным законом полного тока и определением напряженности через магнитный поток, мы можем переписать закон полного тока относительно магнитного потока.
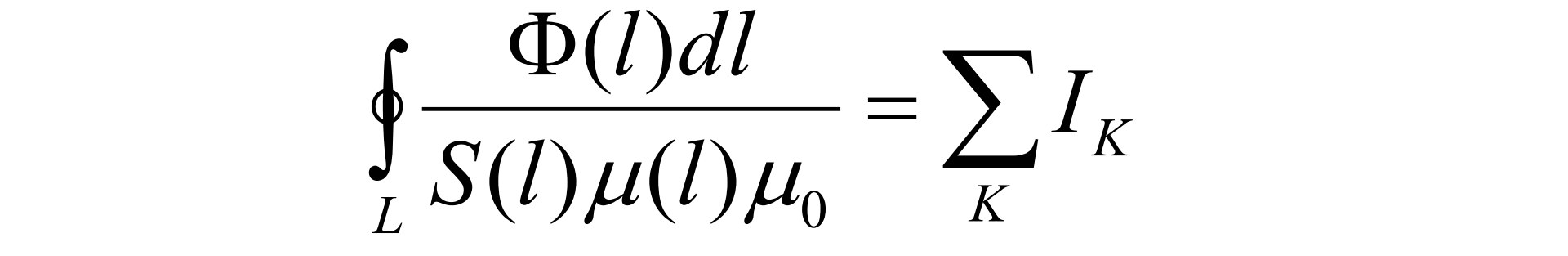
Откуда в уравнении появился и что символизирует аргумент l? Все очень просто. Так как мы рассматриваем контур L, то разумно представить, что на различных его участках наши характеристики могут принимать различные значения: площадь сечения может изменяться, как и магнитная проницаемость либо магнитный поток.
Приобретенное уравнение можно рассматривать как 2-ой закон Кирхгофа, который, напомню, звучит следующим образом:
В хоть какой момент времени алгебраическая сумма напряжений на ветвях контура равна нулю.
Для полной ясности, проведем аналогию между электрическими и магнитными цепями, также их величинами.

Конкретно проведя аналогичное представление для электрической цепи, мы можем рассчитывать магнитные цепи. Для того, дабы это выполнить, следует:
На уровне мыслей разбить сердечник на отдельные однородные участки (непрерывные, с неизменным сечением) без разветвлений и найти их магнитные сопротивления;
Выстроить эквивалентную электрическую цепь, последовательно заменяя участки магнитной цепи участками электрической с электрическими сопротивлениями, также заменяя индуктивности (катушки) на источники ЭДС;
После обозначения данных сопротивлений и ЭДС, можем вычислить в общем токи в элементах электрической цепи;
Произвести подмену приобретенных величин согласно таблице (токи в потоки, ЭДС в МДС [Магнитодвижущую силу / Ампер-витки], а электрическое сопротивление в магнитное сопротивление).
Конкретно таким макаром, мы можем высчитать свойства магнитной цепи. Приобретенные результаты позволяют, к примеру, вычислить индуктивности.
А примеры расчетов будут?
Тут — нет. А по ссылке — да! В данном документе Самарского муниципального технического института рассмотрены базисные примеры, которые позволят лучше разобраться в теме, если она вас заинтриговала. Кроме всего остального, там же приведены теоретические справки. Советую прочесть в надежде, что вы можете себе что-то новое подчерпнуть.
Заключение
Во-1-х, спасибо, что прочитали статью! Один из методов поддержать меня как создателя — подписаться на мой паблик Вконтакте, где время от времени выходят «локальные статьи».
Во-2-х, вернемся к началу статьи. Там я задался целью показать, почему физика изумительна. Не желаю быть многоречивым, потому просто попрошу вспомнить все то, что было описано выше. Мы оперировали моделями, которые относятся к разделу физики электричества и перенесли их на физику магнетизма. Наверное, вы замечали, как нередко встречаются элементы механики в других разделах. Это по настоящему умопомрачительно! Но главное не поработиться иллюзией, что в мире все законы нам максимально известны.
КС. Неизменный ток для полной цепи
где ℰ – ЭДС источника тока (В); Аст – работа посторониих сил по перемещению заряда (Дж); q – величина перемещаемого заряда (Кл).
где I – сила тока в цепи (А); ℰ – ЭДС источника тока (В); R – наружное сопротивление цепи (Ом); r – сопротивление источника (Ом).
При маленьком замыкании сопротивление наружной части цепи стремится к нулю, т.е. R ≈ 0, тогда
где Iкз – ток недлинного замыкания (А); ℰ – ЭДС источника тока (В); r – сопротивление источника (Ом).
Аккумулятор может работать в 2-ух режимах: зарядки и разрядки. В режиме зарядки (другим источником) аккумулятор врубается так, как показано на рис. 1. Ток идет в направлении, обратном направлению тока аккума, потому ЭДС ℰ < 0.
В режиме разрядки аккумулятор врубается так, как показано на рис. 2, потому ЭДС ℰ > 0.
Закон Ома для неоднородного участка цепи
Участок цепи, на котором действуют посторонние силы, именуют неоднородным (рис. 3).
На неоднородном участке цепи сила тока определяется по формуле
где ℰ – ЭДС источника тока (В); φ1 – φ2 – разность потенциалов на участке цепи 1-2 (В); R1/2 = R + r – сопротивление участка 1-2 (Ом).
Символ ЭДС определяем по мнемоническому правилу: при переходе вдоль тока через источник ЭДС берется с последним знаком. К примеру, на рис. 3 а – ЭДС берем со знаком «+»; на рис. 3 б – со знаком «–».
Работа и мощность тока для полной цепи
Для замкнутой цепи, мощность, выделяемая на наружном участке цепи, именуется полезной мощностью. Она равна
С учетом закона Ома для участка цепи \(~I = \dfrac\) полезную мощность можно отыскать, если известны любые две величины из 3-х: I, U, R.
\(~P_p = U \cdot I\) , \(~P_p = I^2 \cdot R\) , \(~P_p = \dfrac\) .
Для замкнутой цепи, мощность, выделяемая на внутреннем сопротивлении источника, именуется теряемой мощностью. Она равна
Полная мощность источника тока равна
\(~P = P_p + P_t\) либо Р = I·ℰ ,
где Р – полная мощность источника тока (Вт); Рp – нужная мощность (Вт); Рt – теряемая мощность (Вт); I – сила тока в цепи (А); R – наружное сопротивление (Ом); r – сопротивление источника (Ом); U – напряжение на участке (В); ℰ – ЭДС источника тока (В).
где η – КПД источника тока; Р – полная мощность источника тока (Вт); Рp – нужная мощность (Вт).
Соединения источников тока
При соединении N источников тока с ℰ1, ℰ2, …, ℰN и сопротивлениями r1, r2, …, rN: последовательно
параллельно одноименными полюсами, если ℰ1 = ℰ2 = … = ℰN , то
Символ ЭДС определяем по мнемоническому правилу: при переходе вдоль тока через источник ЭДС берется с последним знаком.
Правила Кирхгофа
Для упрощения расчета разветвленных цепей, содержащих неоднородные участки, были сделаны особые правила – правила Кирхгофа:
- Алгебраическая сумма сил токов для каждого узла равна нулю: \(~\pm I_1 \pm I_2 \pm \ldots \pm I_N = 0\) . Правило символов для токов в узлах:
- если ток втекает в узел, то силу тока берем со знаком «+»,
- если ток вытекает из узла, то со знаком «–».
К примеру, на рисунке 4 со знаком «+» берем I1 и I4, со знаком «–» – I2, I3 и I5. Тогда для узла А можно записать, что I1 — I2 — I3 + I4 — I5 = 0.
- если направление тока совпадает с направлением обхода контура, то силу тока берем со знаком «+»,
- если направление тока не совпадает с направлением обхода контура, то силу тока берем со знаком «–».
- если направление тока источника совпадает с направлением обхода контура, то ЭДС источника берем со знаком «+»,
- если направление тока источника не совпадает с направлением обхода контура, то ЭДС источника берем со знаком «–».
- символ ЭДС соответствует знаку последней клеммы источника при переходе через источник по обходу контура.
Цепи с конденсаторами
Для расчета цепей с конденсаторами применяются следующие правила.
- Если несколько конденсаторов соединены параллельно, то C = C1 + C2 + C3 + … + CN , q = q1 + q2 + q3 + … + qN .
- Если несколько конденсаторов соединены последовательно, то \(~\frac= \frac+ \frac+ \frac+ \ldots + \frac\) , q = q1 = q2 = q3 = … = qN .
- Если пластинки нескольких конденсаторов соединены в один узел, не связанный конкретно с источником тока, то алгебраическая сумма зарядов на этих пластинках равна нулю (закон сохранения заряда): q1 + q2 + q3 + … + qN = 0 . К примеру, для цепи на рис. 6. 0 = —q1 + q2 + q3 .
Закон тока для полной цепи
14. Работа и мощность в цепи неизменного тока. Электродвижущая сила. Закон Ома для полной цепи
Из формулы определения напряжения () просто получить выражение для расчета работы по переносу электрического заряда ; так как сила тока связана с зарядом соотношением , то работа тока: , либо .
Мощность по определению , поэтому, .
Российский ученый X. Ленц и британский учены Д. Джоуль опытным методом посреди XIX в. установили независимо друг от друга закон, который именуется законом Джоуля—Ленца и читается так: при прохождении тока по проводнику количество теплоты, выделившееся в проводнике, прямо пропорцинально квадрату силы тока, сопротивлению проводника и времени прохождения тока:
Полная замкнутая цепь представляет собой электрическую цепь, в состав которой входят наружные сопротивления и источник тока (рис. 17). Как один из участков цепи, источник тока обладает сопротивлением, которое именуют внутренним, .
Для того дабы ток проходил по замкнутой цепи, нужно, дабы в источнике тока зарядам сообщались дополнительная энергия, она возникает за счет работы по перемещению зарядов, которую создают силы неэлектрического происхождения (посторонние силы) против сил электрического поля. Источник тока характеризуется энергетической чертой, которая именуется ЭДС — электродвижущая сила источника. ЭДС измеряется отношением работы посторониих сил по перемещению вдоль замкнутой цепи положительного заряда к величине этого заряда .
Пусть за время через поперечное сечение проводника пройдет электрический заряд . Тогда работу посторониих сил при перемещении заряда можно записать так: . Согласно определению силы тока, , потому . При совершении этой работы на внутреннем и наружном участках цепи, сопротивления которых и , выделяется некоторое количество теплоты. По закону Джоуля—Ленца оно равно: . Согласно закону сохранения энергии, . Поэтому, . Произведение силы тока на сопротивление участка цепи нередко именуют падением напряжения на этом участке. Таким макаром, ЭДС равна сумме падений напряжений на внутреннем и наружном участках замкнутой цепи. Как правило это выражение записывают так: . Эту зависимость опытным методом получил Георг Ом, именуется она законом Ома для полной цепи и читается так: сила тока в полной цепи прямо пропорциональна ЭДС источника тока и назад пропорциональна полному сопротивлению цепи. При разомкнутой цепи ЭДС равна напряжению на зажимах источника и, поэтому, может быть измерена вольтметром.
1. Согласно закону Ома для участка цепи, сила тока прямо пропорционально напряжению и назад пропорционально сопротивлению проводника. Выразив отсюда сопротивление , некоторые абитуриенты делают неверный вывод, что сопротивление проводника находится в зависимости от напряжения и силы тока. Эта ошибка свидетельсвует о формальном усвоении закона Ома и недопонимании его физической сути.
Напрядение и сила тока не определеют сопротивление. Формула закона Ома отражает тот факт, что для данного проводника () сила тока тем больше, чем больше напряжение. График зависимости представляет собой прямую линию и именуется вольт-амперной чертой проводника.
[правил ]