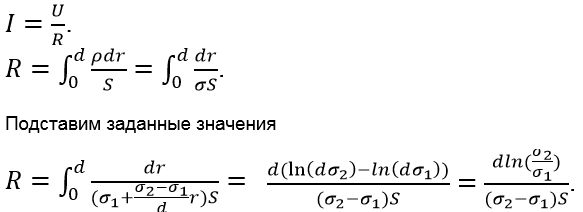Закон ома в интегральной форме

Закон Ома в интегральной форме предполагает, что рассматривается полный ток, протекающий в цепи и величина тока с течением времени не изменяется.

Тогда закон Ома для участка цепи, содержащей э.д.с., будет иметь вид:

3) Если замкнутый участок цепи, содержит э.д.с., тогда φ1 = φ2, и получаем:

— закон Ома для замкнутого участка цепи, содержащего э.д.с.

В целом участок цепи, содержащей огромное количество э.д.с. и различных деталей представлен законом Ома в виде:

Из закона Ома следует:

2.3.1 Закон Ома в дифференциальной форме

Сечение проводника либо частей цепи, обычно, неоднородно, и сопротивляемость в различных участках цепи протеканию тока также разная. Тогда разбивают участки цепи на элементы (дифференцируют) и определяют закон Ома в каждом отдельно взятом участке.

— закон Ома, тогда для каждого участка цепи сечением ∆S и длиной ∆l можно записать закон Ома как: .

Беря во внимание, что для участка цепи

Это закон Ома в дифференциальной форме. Зная, что удельная электропроводность σ и удельное сопротивление ρ связаны, как:

, где σ — удельная электропроводность, ρ — удельная сопротивление,

— закон Ома в дифференциальной форме.

17.Работа неизменного тока в проводнике. Мощность. КПД источника тока в электрической цепи. Закон Джоуля-Ленца в дифференциальной и интегральной формах.

Работа тока — работа электрического поля по переносу электрических зарядов вдоль проводника;

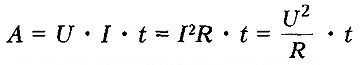
ЗАКОН ДЖОУЛЯ -ЛЕНЦА

При прохождениии тока по проводнику проводник греется, и происходит термообмен с окружающей средой, т.е. проводник дает теплоту окружающим его телам.

Количество теплоты, выделяемое проводником с током в окружающую среду, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.

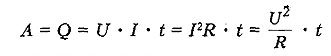
Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: большая плотность термический мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля

МОЩНОСТЬ Неизменного ТОКА- отношение работы тока за время t к этому интервалу времени.

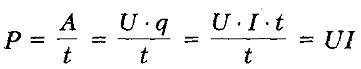
18. Традиционная электронная теория электропроводности. Вывод закона Ома.

По теории Друде — Лоренца, электроны владеют таковой же энергией термического движения, как и мо­лекулы одноатомного газа. Потому, при­меняя выводы молекулярно-кинетической теории (см. (44.3)), можно отыскать среднюю скорость термического движения электронов

которая для T=300 К равна 1,1•10 5 м/с. Термическое движение электронов, являясь хаотическим, не может привести к возник­новению тока.

Друде считал, что сходу после еще одного соударения электрона с ионом кристаллической решетки скорость упорядоченного движения электрона равна нулю. Представим, что напряженность поля не меняется. Тогда под действием поля электрон получит неизменное ускорение равное

и к концу пробега скорость упорядоченного движения достигнет значения

где t — среднее время между 2-мя последовательными соударениями электрона с ионами решетки. Друде не учитывал рассредотачивание электронов по скоростям и приписывал всем электронам однообразное значение средней скорости . В этом приближении , где — среднее значение длины свободного пробега, — скорость термического движения электронов. Подставим это значение t в формулу (18.2)

Скорость меняется за время пробега линейно. Потому ее среднее (за пробег) значение равно половине наибольшего

Подставив это выражение в

Плотность тока оказалась пропорциональной напряженности поля. Поэтому, мы получили закон Ома. Согласно коэффициент пропорциональности между j и Е представляет собой проводимость

Электрический ток. Сила и плотность тока. Главные законы неизменного тока. Законы Ома и Джоуля-Ленца в интегральной и дифференциальной формах. Плотность тока и скорость носителей тока.

I. Хоть какое упорядоченное (направленное) движение электрических зарядов именуется ЭЛЕКТРИЧЕСКИМ ТОКОМ. При приложении наружного электрического поля Е в проводнике начинается движение зарядов, т.е. появляется электрический ток. При всем этом положительные заряды движутся по полю, а отрицательные — против поля. За направление тока принимают направление движения положительных зарядов. Для появления и существования электрического тока нужно выполнение 2-ух критерий :

1. наличие свободных носителей зарядов (т.е. вещество должно быть проводником либо полупроводником при больших температурах),

2.Наличие наружного электрического поля.

Для количественного описания электрического тока вводится — СИЛА ТОКА – скалярная физическая велична, равная количеству электрического заряда, переносимосму за единицу времени через поперечное сечение проводника S.

— для неизменного тока, и

— для переменного тока.

Ток, сила и направление которого не меняются с течением времени, именуетсянеизменным.

ПЛОТНОСТЬ ТОКА — векторная физическая величина, численно равная силе тока, проходящего через единицу площади, перпендикулярной к току:

1. Закон Ома для однородного участка цепи.

Однороднымименуется участок не содержащий ЭДС.

Сила тока на однородном участке цепи прямо пропорциональна напряжению и назад пропорциональна сопротивлению цепи

1 Ом – сопротивление такового проводника, в каком при напряжении 1 В течёт ток 1 А.

G — электрическая проводимость. (Сименс).

Сопротивление R проводника находится в зависимости от его размеров и формы, также от материала проводника.

,

где ρ — удельное сопротивление проводника — сопротивление единицы длины проводника.

ℓ — длина проводника; S — площадь поперечного сечения проводника.

2.Закон Ома для неоднородного участка цепи

НЕОДНОРОДНЫМименуется участок цепи, содержащий ЭДС.

— Закон Ома для неоднородного участка цепи в интегральной форме.

3. Закон Ома для замкнутой цепи (для полной цепи).

где где R — сопротивление наружной цепи,

г — сопротивление источника ЭДС, тогда

— Закон Ома для полной цепи

4. Закон Ома в дифференциальной форме.

σ — удельная электропроводность;

— Закон Ома в дифференциальной форме.

Плотность тока прямо пропорциональна напряженности электрического поля Е, Коэффициент пропорциональности σ — удельная электропроводность.

Если в проводнике течет неизменный ток и проводник остается недвижным, то работа посторониих сил расходуется на его нагревание. Опыт указывает, что в любом проводнике происходит выделение теплоты, равное работе, совершаемой электрическими силами по переносу заряда вдоль проводника. Если на концах участка проводника имеется разность потенциалов , тогда работу по переносу заряда q на этом участке равна

По определению I= q/t. откуда q= I t. Поэтому

Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил

Соотношение (17.13) выражает закон Джоуля-Ленца в интегральной форме. Введем плотность термический мощности , равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника

где S — поперечное сечение проводника, — его длина. Используя (1.13) и соотношение , получим . Но — плотность тока, а , тогда с учетом закона Ома в дифференциальной форме , совсем получаем

Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: большая плотность термический мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.

Подвижность (скорость) носителей тока в твёрдом теле, отношение скорости направленного движения электронов проводимости и дырок (дрейфовой скорости υдр), вызванного электрическим полем, к напряжённости Е этого поля:

У различных типов носителей в одном и том же веществе μ различны, а в анизотропных кристаллахразличны μ каждого типа носителей для различных направлений поля Е. Величина μ определяется процессамирассеяния электронов в кристалле. Рассеяние происходит на заряженных и нейтральных примесныхчастицах и недостатках кристаллической решётки, также на термических колебаниях кристаллической решётки (фононах). Испуская либо поглощая фонон, носитель изменяетсвой Квазиимпульс и, поэтому, скорость. Потому μ сильно меняется при изменении температуры.При T ≥ 300 К преобладает рассеяние на фононах, с снижением температуры возможность этого процессападает и доминирующим становится рассеяние на заряженных примесях либо недостатках, вероятностькоторого вырастает с уменьшением энергии носителей.

Законы Кирхгофа.

1-ый закон Кирхгофа.

1) 1-ый закон (правило) Кирхгофа — алгебраическая сумма токов сходящихся в узле равна нулю.

Ветки — это проводящие участки цепи между узлами.

Узел — это область соединения 2-ух (либо трёх) и поболее веток.

Алгебраическая сумма — это означает в неё входят слагаемые со знаком плюс и со знаком минус.

На рисунке ниже показан узел в каком соединяются четыре ветки с токами: I1, I2, I3, I4.

Набросок 1 — Узел с ветвями
Направления токов показаны стрелочками. От узла ориентированы токи I1 и I2, к узлу ориентированы токи I3 и I4. Примем направления к узлу — положительными, а от узла — отрицательными. Запишем, с учётом избранных положительных и отрицательных направлений токов, уравнение по первому закону Кирхгофа для узла на рисунке 1:

Ток I1 вошел в уравнение (1) со знаком минус так как этот ток ориентирован от узла (см. набросок 1).

Ток I2 заходит в уравнение (1) со знаком минус по той же причине. Токи I3 и I4 входят в уравнение (1) со знаком плюс так как они ориентированы к узлу (см. набросок 1). Вся эта алгебраическая сумма равна нулю.

Токи I1 и I2 можно перенести в правую часть уравнения с обратным знаком:

Также можно поступить и с хоть каким уравнением записанным по первому закону Кирхгофа.

Беря во внимание это можно дать другое определение первого закона (правила) Кирхгофа:

2) сумма токов входящих в узел равна сумме токов выходящих из него.

Уравнение (2) можно привести к виду:

перенеся в правую часть уравнения токи I3 и I4 с обратным знаком.
Уравнение (3) можно привести к виду:

Тоже самое можно сделать с хоть каким уравнением записанным по первому закону Кирхгофа. Это означает что не имеет значения то какое направление (от узла либо к узлу) принято за положительное а какое за отрицательное, главное дабы все однообразные направления имели один символ а все обратные другой.

Время от времени случается так что один узел принимается за два и поболее при невнимательном осмотре схемы что приводит к ошибкам в расчётах. Разглядим схему на рисунке 2:

Набросок 2 — Схема с одним узлом

В этой схеме один узел, для этого узла можно составить уравнение по первому закону Кирхгофа:

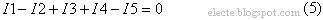
Токи в узлах не протекают т.к. узел имеет один потенциал на всем его протяжении и на всей его площади.