Электрический ток — это направленное движение заряженных частиц, при котором происходит перенос заряда из одних областей места в другие.
Сила тока — количественная черта электрического тока. В случае неизменного тока абсолютная величина силы тока есть отношение абсолютной величины заряда \(q\) , прошедшего через поперечное сечение проводника за время \(t\) , к этому времени. \[I=\dfrac\]
Единицы измерения: \(\displaystyle [\text]\) (Ампер).
Электродвижущая сила (ЭДС)
Посторонняя сила \(\vec_\text\) не имеет дела к стационарному электрическому полю.
Эта величина именуется электродвижущей силой (ЭДС) источника тока.
Единицы измерения: \(\displaystyle [\text]\) (Вольт).
Электрическое напряжение между точками A и B электрической цепи либо электрического поля — физическая величина, значение которой равно работе действенного электрического поля, совершаемой при переносе единичного пробного заряда из точки A в точку B.
Единицы измерения: \(\displaystyle [\text]\) (Вольт).
Закон Ома для участка цепи
Омическое сопротивление \(R\) — сопротивление цепи неизменному току, вызывающее невозвратные энергопотери неизменного тока.
Единицы измерения: \(\displaystyle [\text]\) (Ом).
Сопротивление проводника прямо пропорционально его длине \(l\) и назад пропорционально площади поперечного сечения \(S\) :
Коэффициент пропорциональности \(\rho\) — удельное сопротивление данного вещества.
Единицы измерения: \(\displaystyle [\text\cdot\text]\) (Ом на метр).
Зависимость удельного сопротивления от температуры
Множитель \(\alpha\) именуется температурным коэффициентом сопротивления. Его значения для разных металлов и сплавов можно отыскать в таблицах.
\(\rho_0\) — удельное сопротивление проводника при \(0^oC\) .
Последовательное и параллельное соединение проводников
Последовательное соединение проводников
Параллельное соединение проводников
Закон Ома для полной цепи
Сила тока в полной цепи прямо пропорциональна ЭДС и назад пропорциональна полному сопротивлению цепи, где под полным сопротивлением понимается сумма наружных и внутренних сопротивлений.
Единицы измерения: \(\displaystyle [\text]\) (Джоуль).
Мощность тока — отношение работы тока ко времени, за которое эта работа совершена.
Единицы измерения: \(\displaystyle [\text]\) (Ватт).
Пусть на рассматриваемом участке цепи не совершается механическая работа и не протекают хим реакции. Работа поля \(A\) полностью преобразуется в тепло \(Q=A\) .
1-ое правило Кирхгофа
Алгебраическая сумма токов веток, сходящихся в каждом узле хоть какой цепи, равна нулю.
Также можно просто уяснить 1-ый закон Кирхгофа следующим образом: сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.
Тут ток \(I_1\) — ток, втекающий в узел, а токи \(I_2\) и \(I_3\) — токи, вытекающие из узла. Тогда можно записать:
\(I_1 = I_2 + I_3,\ (1)\)
Перенесем токи \(I_2\) и \(I_3\) в левую часть выражения (1), тем получим:
\(I_1 — I_2 — I_3 = 0,\ (2)\)
Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.
Знаки для втекающих и вытекающих токов можно брать произвольно, но в главном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «—».
2-ое правило Кирхгофа
Алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур.
Термин «алгебраическая сумма» значит, что как величина ЭДС, так и величина падения напряжения на элементах может быть как со знаком «+», так и со знаком «—». При всем этом найти символ можно по следующему методу:
1. Избираем направление обхода контура (два варианта: или по часовой стрелке, или против).
2. Произвольно избираем направление токов через элементы цепи.
3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:
— ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура, записываются со знаком «+», в неприятном случае ЭДС записываются со знаком «—».
— напряжения, падающие на элементах цепи, записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в неприятном случае напряжения записываются со знаком «—».
К примеру, разглядим цепь на рисунке и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке и выбрав направление токов через резисторы, как показано на рисунке.
Закон Ома для цепей переменного и неизменного тока
Закон Ома является одним из главных законов электротехники. Он достаточно прост и используется при расчете фактически всех электрических цепей. Но данный закон имеет некоторые особенности работы в цепях переменного и неизменного тока при наличии в цепи реактивных частей. Эти особенности необходимо держать в голове всегда.
Закон Ома для цепи неизменного тока
Традиционная схема закона Ома смотрится так:
А звучит и того проще – ток, протекающей на участке цепи, будет равен отношению напряжения цепи к ее сопротивлению, что выражается формулой:
Но ведь мы знаем, что кроме активного сопротивления R, существует и реактивные сопротивления индуктивности ХL и емкости XC. А ведь согласитесь, что электрические схемы с чисто активным сопротивлением встречаются очень изредка. Давайте разглядим схему, в какой последовательно включена катушка индуктивности L, конденсатор С и резистор R:
Кроме чисто активного сопротивления R, индуктивность L и емкость С имеют и реактивные сопротивления ХL и XC, которые выражены формулами:
Где ω это повторяющаяся частота сети, равная ω = 2πf. f – частота сети в Гц.
Для неизменного тока частота равна нулю (f = 0), соответственно реактивное сопротивление индуктивности станет равным нулю (формула (1)), а емкости – бесконечности (2), что приведет к разрыву электрической цепи. Отсюда можно прийти к выводу, что реактивное сопротивление частей в цепях неизменного напряжения отсутствует.
Закон Ома для цепи переменного тока
Если рассматривать традиционную электрическую цепь и на переменном токе, то она фактически ничем не будет отличаться от неизменного тока, только источником напряжения (заместо неизменного — переменное):
Соответственно и формула для такового контура остается прежней:
Но если мы усложним схему и добавим к ней реактивных частей:
Ситуация поменяется кардинально. Сейчас f у нас не равна нулю, что говорит о том, что кроме активного, в цепь вводится и реактивное сопротивление, которое также может оказывать влияние на величину тока, протекаемого в контуре и приводить к резонансу. Сейчас полное сопротивление контура (обозначается как Z) и оно не равно активному Z ≠ R. Формула воспримет следующий вид:
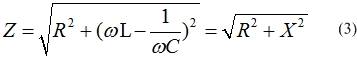
Соответственно малость поменяется и формула для закона Ома:
Почему это принципиально?
Познание этих аспектов дозволит избежать суровых заморочек, которые могут появиться при неверном подходе к решению некоторых электротехнических задач. К примеру, в контур переменного напряжения подключена катушка индуктивности со следующими параметрами: fном = 50 Гц, Uном = 220 В, R = 0,01 Ома, L = 0,03 Гн. Ток, протекающий через данную катушку будет равен:
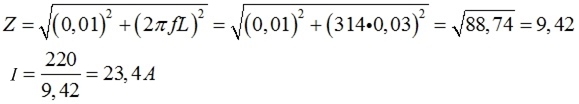
В случае, если подать на эту же катушку неизменное напряжение с таким же значением, получим:
Мы лицезреем, что ток катушки увеличивается в разы, что приводит к выходу из строя частей контура.






