1 Отыскать плотность тока, если за время t=10 с через поперечное сечение проводника протекает заряд q=100 Кл. Площадь поперечного сечения проводника S=5 мм2.
Ток в проводнике I=q/t. Плотность тока j=I/S; отсюда j=q/tS=2 кА/м2.
2 Вольтметр рассчитан на измерение напряжений до наибольшего значения V=3 В. Сопротивление устройства R = 300 Ом. Число делений шкалы устройства N=100. Какова будет стоимость деления шкалы устройства, если применять его в качестве миллиамперметра?
Стоимость деления шкалы устройства как миллиамперметра i = I/N=V/RN=0,1 мА/дел.
3 Каким сопротивлением должен владеть устройство, дабы его можно было применять или в качестве вольтметра с пределом измерения напряжений до значений V=15 B, или в качестве миллиамперметра с пределом измерения токов до значений I=7,5 мА?
Сопротивление устройства R=V/I=2кОм.
4 Отклонение стрелки вольтметра до конца шкалы соответствует напряжению V0 = 15 В. При всем этом через вольтметр течет ток I0 = 1,5 мА. Отыскать сопротивление вольтметра и ток, текущий через вольтметр, когда он указывает напряжение V= 5 В.
Сопротивление вольтметра найдем из условия, что при отклонении стрелки на всю шкалу напряжение на зажимах устройства равно V0, а ток, текущий через устройство, равен I0: R= V0/I0 — 2 кОм. Когда же вольтметр указывает напряжение V, то через него течет ток I=V/R = I0V/V0 = 2,5 мА.
5 Отыскать ток в цепи источника тока, замкнутого на проводник с сопротивлением R=1000 Ом, если при последовательном включении в эту цепь миллиамперметра с сопротивлением R0 = 100bОм он показал ток I0 = 25 мА.
6 Отыскать напряжение на проводнике с сопротивлением R=10Ом, если за время t=5 мин протекает заряд q= 120 Кл.
Закон Ома для участка цепи. Сопротивление проводников
7 В электрическую сеть последовательно включены плитка, реостат и амперметр, имеющие сопротивления R1 = 50Ом, R2 = 30 Ом и R3 = 0,1 Ом. Отыскать напряжения на плитке, реостате и амперметре, если в цепи протекает ток I = 4 А.
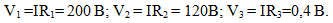
8 Сопротивление единицы длины медной проволоки Rl = R/l=2,23 Ом/м. Отыскать удельное сопротивление r меди. Поперечник проволоки D = 0,1 мм.
9 Отыскать сопротивление R медной проволоки, масса которой m = 1 кг, а площадь поперечного сечения S=0,1 мм2. Плотность меди , ее удельное сопротивление r = 0,017 мкОм м.
10 Удельное сопротивление графитового стержня от карандаша r = 400 мкОм м. Какой ток I пройдет по стержню, если на него подать напряжение V=6 В? Длина стержня l=20 см, его поперечник D = 2 мм.
11 При включении в электрическую цепь проводника, имеющего поперечник D = 0,5 мм и длину l=47 мм, напряжение на нем V=1,2В при токе в цепи I=1 А. Отыскать удельное сопротивление r материала проводника.
12 Электрическая цепь состоит из 3-х последовательно соединенных кусков провода одинаковой длины, изготовленных из 1-го материала, но имеющих различные сечения: S1 = 1 мм2, S2 = 2мм2, S3 = 3 мм2. Напряжение на концах цепи V= 11 В. Отыскать напряжение на каждом проводнике.
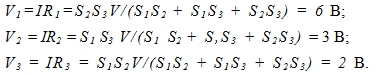
13 Для измерения температуры применили металлическую проволочку, имеющую при температуре t1 = 10°С сопротивление R1 = 15 Ом. При некоторой температуре t2 она имела сопротивление R2 = 18,25 Ом. Отыскать эту температуру. Температурный коэффициент сопротивления железа
При температурах t1 и t2 сопротивления проволочки
где R0-ее сопротивление при to = 0°C. Разыскиваемая температура
14 Отыскать температуру t2 вольфрамовой нити лампочки, если при включении в сеть с напряжением V=220 В по нити идет ток I=0,68 А. При температуре t1 = 20° С сопротивление нити R = 36 Ом. Температурный коэффициент сопротивления вольфрама
Главные законы цепей неизменного тока
Расчет и анализ электрических цепей делается с внедрением закона Ома, первого и второго законов Кирхгофа. На базе этих законов устанавливается связь между значениями токов, напряжений, ЭДС всей электрической цепи и отдельных ее участков и параметрами частей, входящих в состав этой цепи.
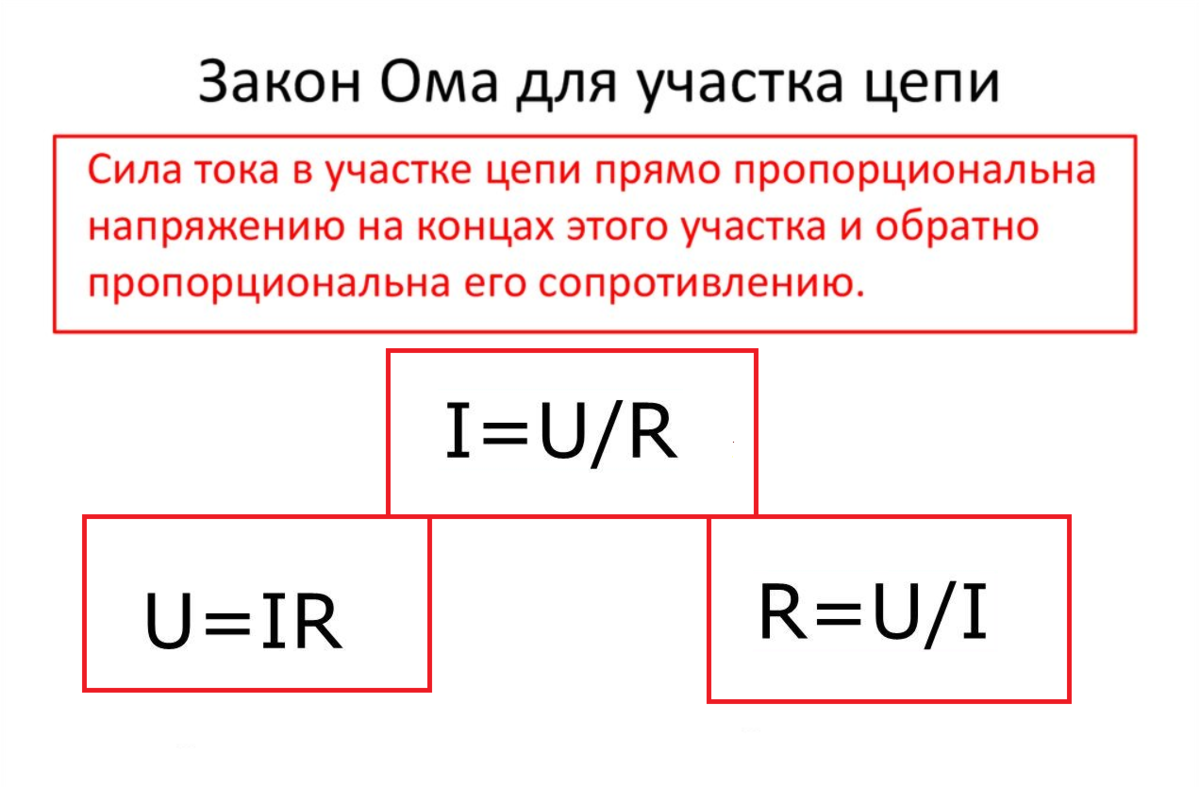
Закон Ома для участка цепи
Соотношение между током I, напряжением UR и сопротивлением R участка аb электрической цепи (рис. 1.3) выражается законом Ома
В данном случае UR = RI – именуют напряжением
либо падением напряжения на резисторе R, а – током в резисторе R.
При расчете электрических цепей время от времени удобнее воспользоваться не сопротивлением R, а величиной оборотной сопротивлению, т.е. электрической проводимостью:
.
В данном случае закон Ома для участка цепи запишется в виде:
Закон Ома для всей цепи
Этот закон определяет зависимость между ЭДС Е источника питания с внутренним сопротивлением r0 (рис.1), током I электрической цепи и общим эквивалентным сопротивлением RЭ = r0 + R всей цепи:
.
Непростая электрическая цепь содержит, обычно, несколько веток, в которые могут быть включены свои источники питания и режим ее работы не может быть описан только законом Ома. Но это можно выполнить на основании первого и второго законов Кирхгофа, являющихся следствием закона сохранения энергии.
1-ый закон Кирхгофа
В любом узле электрической цепи алгебраическая сумма токов равна нулю
,
где m – число веток присоединенных к узлу.
При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус». К примеру, для узла а (см. рис. 1) I — I1 — I2 = 0.
2-ой закон Кирхгофа
В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках
,
где n – число источников ЭДС в контуре; m – число частей с сопротивлением Rк в контуре; Uк = RкIк – напряжение либо падение напряжения на к-м элементе контура.
Для схемы (рис. 1) запишем уравнение по второму закону Кирхгофа:
Если в электрической цепи включены источники напряжений, то 2-ой закон Кирхгофа формулируется в следующем виде: алгебраическая сумма напряжений на всех элементах контура, включая источники ЭДС равна нулю
.
При записи уравнений по второму закону Кирхгофа нужно:
1) задать условные положительные направления ЭДС, токов и напряжений;
2) избрать направление обхода контура, для которого записывается уравнение;
3) записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, при этом слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они обратны.
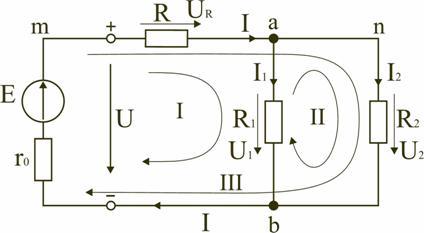
Рис.2
Запишем уравнения по II закону Кирхгофа для контуров электрической схемы (рис. 2):
В действующей цепи электрическая энергия источника питания преобразуется в другие виды энергии. На участке цепи с сопротивлением R в течение времени t при токе I расходуется электрическая энергия
Скорость преобразования электроэнергии в другие виды представляет электрическую мощность
.
Из закона сохранения энергии следует, что мощность источников питания в хоть какой момент времени равна сумме мощностей, используемой на всех участках цепи.
.
Это соотношение (1.8) именуют уравнением баланса мощностей. При составлении уравнения баланса мощностей следует учитывать, что если действительные направления ЭДС и тока источника совпадают, то источник ЭДС работает в режиме источника питания, и произведение E I подставляют в (1.8) со знаком плюс. Если не совпадают, то источник ЭДС работает в режиме потребителя электроэнергии, и произведение E I подставляют в (1.8) со знаком минус. Для цепи, показанной на рис. 1.2 уравнение баланса мощностей запишется в виде:
Схемы соединения приёмников электрической цепи.
Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы на рис. 1.3, где R=Rэкв, а расчет токов и напряжений делается при помощи законов Ома и Кирхгофа.
Категория: Закон Ома
Расчет падений напряжений между разными точками, определение токов и напряжений в цепи в том числе с внедрением законов Кирхгофа – вот что нас ожидает в этой статье. Задачка 1. В батарее, изображенной на рисунке, В, Ом, В‚ Ом‚ В, Ом; Ом‚ Ом. Отыскать ЭДС и внутреннее сопротивление этой батареи. Внутренние сопротивления просто сложим (соединены последовательно):….
2017-09-25 | Создатель: Анна
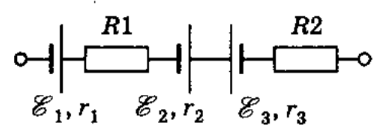
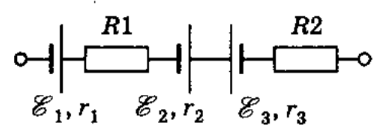
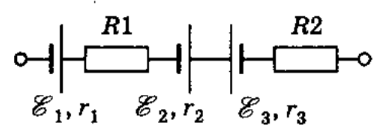
Неизменный ток: КПД источника
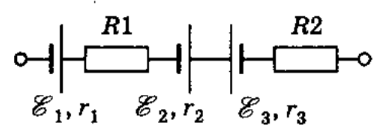
Опять нас ожидает определение внутреннего сопротивления источника, но задачи поинтереснее. Тут непременно будем использовать или выделившуюся в виде тепла энергию, или мощность. Также определим КПД источника тока. Задачка 1. Аккумулятор с ЭДС В и внутренним сопротивлением Ом замкнут медной проволокой, масса которой г. Сопротивление проволоки подобрано так, что во наружной цепи выделяется большая мощность. На….
2017-09-23 | Создатель: Анна


Неизменный ток: источники тока

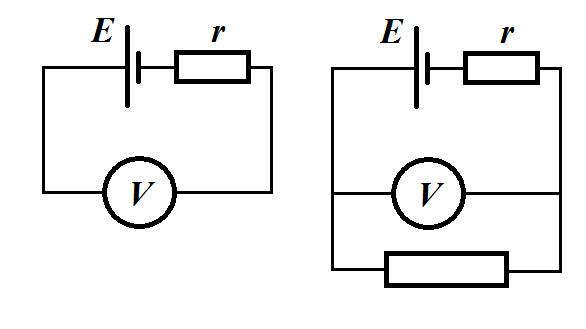
Задачи будут связаны с наличием у источника внутреннего сопротивления, и неминуемым падением на нем напряжения. Потому напряжение на зажимах всегда меньше ЭДС источника. Задачка 1. Вольтметр, присоединенный к зажимам источника тока, показал напряжение В. Когда к этим же зажимам подключили к тому же резистор, вольтметр стал демонстрировать напряжение В. Что покажет вольтметр, если заместо 1-го подключить два….
2017-09-21 | Создатель: Анна
Внутреннее сопротивление источника-2
Эта статья поможет разобраться с источниками: что такое куцее замыкание, напряжение на зажимах, как отыскать внутреннее сопротивление источника. Задачка 1. При подключении лампочки к источнику тока с В напряжение на лампочке В, а ток в ней А. Каково внутреннее сопротивление источника? Падение напряжения на лампочке равно 4 В, поэтому, В падает на внутреннем сопротивлении источника…..
2017-08-20 | Создатель: Анна
Внутреннее сопротивление источника
На внутреннем сопротивлении источника, как и на наружном, происходит падение напряжения. Потому напряжение на зажимах источника меньше ЭДС как раз на данную величину. Задачка 1. Гальванический элемент с ЭДС В и внутренним сопротивлением Ом замкнут накоротко. Найти силу тока недлинного замыкания. При маленьком замыкании сопротивляться току будет только внутреннее сопротивление источника: Ответ: 3….
2017-08-18 | Создатель: Анна
Неизменный ток: мощность тока
Рассчитаем мощность тока в нескольких задачках. Задачи различные: будем и лампочки соединять, и сопротивления рассчитывать, и определять КПД подъемного крана. Задачка 1. В сеть напряжением В параллельно включены две лампы: Л1 мощностью Вт, рассчитанная на напряжение 120 В, и Л2 -12-вольтная лампа, включенная последовательно с проводником . Лампа Л2 работает в номинальном режиме. Найти показания….
2017-07-08 | Создатель: Анна
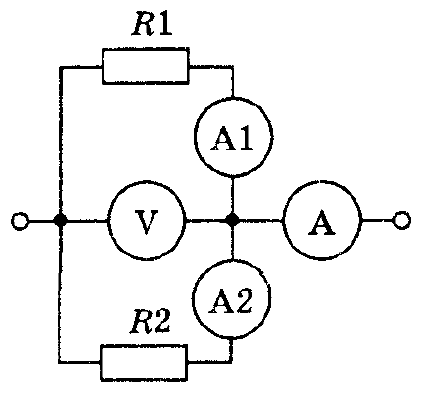


Неизменный ток: сопротивления, закон Ома-2

Разберем в этой статье более сложные задачи. Они все связаны с применением закона Ома, также применением формул пересчета последовательно и параллельно соединенных сопротивлений. Задачка 1. Амперметр А указывает силу тока А при напряжении В. Сопротивление Ом. Найти сопротивление и показания амперметров и . Амперметр указывает ток в неразветвленной части цепи: суммарный ток обеих веток…..
2017-07-02 | Создатель: Анна
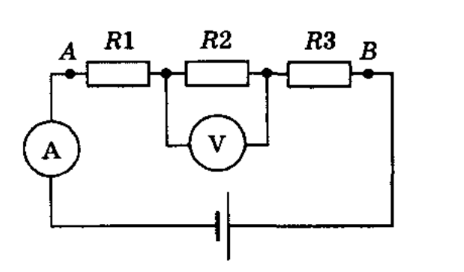


Неизменный ток: измерительные приборы
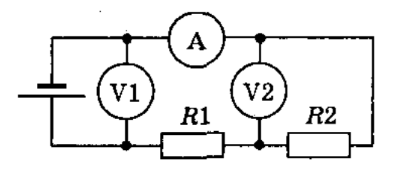
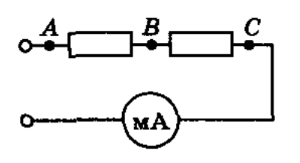
В этой статье мы продолжаем знакомство с темой “неизменный ток”. Задачи тут собраны довольно обыкновенные, статья нацелена на готовящихся к ОГЭ ребят. Задачка 1. В цепь включены последовательно три проводника сопротивлением Ом, Ом, Ом . Какую силу тока указывает амперметр и каково напряжение между точками А и В, если показание вольтметра В? Если на резисторе сопротивлением….
2017-06-30 | Создатель: Анна


Неизменный ток: сопротивления и закон Ома

Разглядим сейчас самые обыкновенные задачи на тему “неизменный ток”. Нам пригодится формула сопротивления зависимо от материала, длины и сечения и закон Ома. Удельные сопротивления материалов можно поглядеть в таблице. Задачка 1. Участок цепи состоит из металлической проволоки длиной м с площадью поперечного сечения мм, соединенной последовательно с никелиновой проволокой длиной м и площадью поперечного сечения мм…..