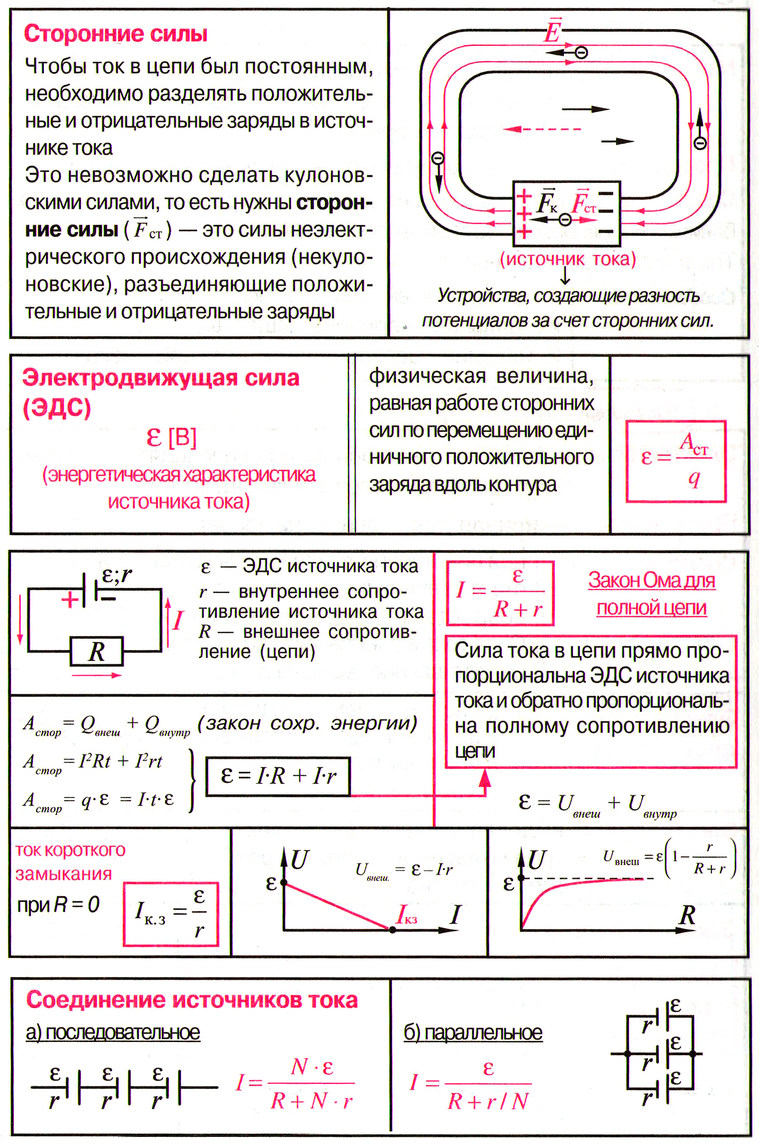
Силы, вызывающие перемещение электрических зарядов снутри источника неизменного тока против направления деяния сил электростатического поля, именуются посторонними силами. Отношение работы посторониих сил Aст по перемещению заряда Q вдоль цепи, к значению этого заряда именуется электродвижущей силой источника (ЭДС)
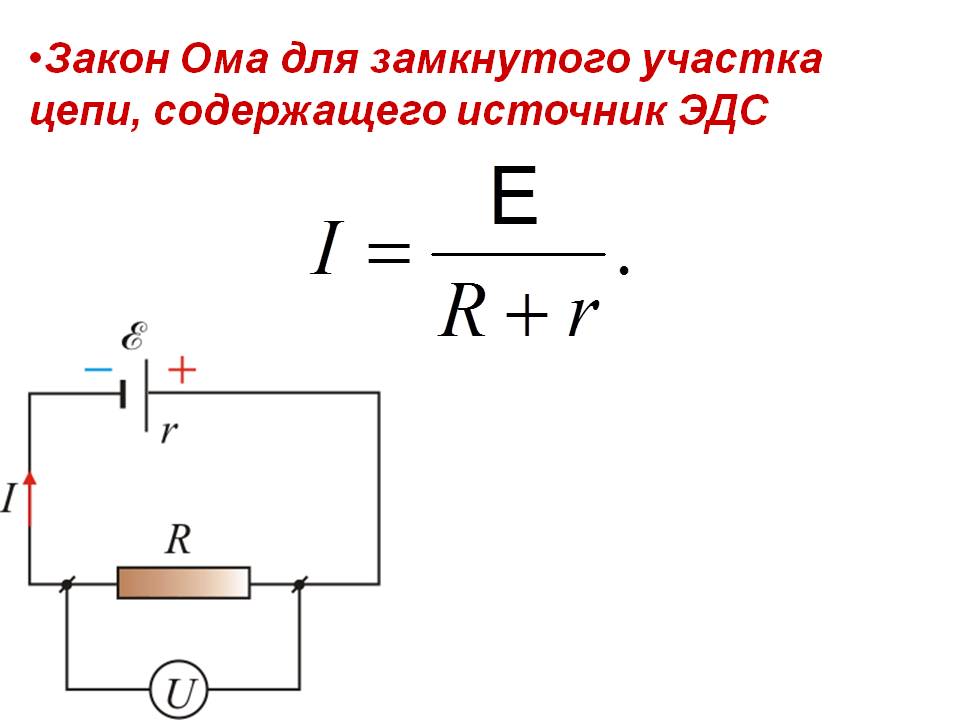
Закон Ома для полной цепи: сила тока I в электрической цепи прямо пропорциональна электродвижущей силе E источника тока и назад пропорциональна сумме электрических сопротивлений наружного R и внутреннего r участка цепи:
В случае, когда сопротивление наружного источника равно нулю (источник тока замкнут накоротко) сила тока максимальна и именуется током недлинного замыкания
Для участка цепи содержащей источник ЭДС закон Ома имеет вид
символ «+» ставится, если ЭДС содействует повышению тока, «-» если уменьшению.
Закон Джоуля-Ленца. Работа и мощность электрического тока.
Закон Джоуля-Ленца: количество тепла Q выделяемое на участке проводника при прохождении тока пропорционально времени прохождения тока, сопротивлению проводника и квадрату силы тока
Работа сил электрического поля, создающего электрический ток,
именуется работой тока:
Мощность электрического тока равна отношению работы тока A ко времени Dt, за которое эта работа совершена:
Нужная мощность – мощность, выделяющаяся на наружном сопротивлении
Полная мощность развиваемая источников равна мощности, которая выделяется во всей цепи
Коэффициент полезного деяния (КПД) источника тока равен отношению полезной мощности, выделяемой в цепи, к отношению полной мощности:
Разветвленные цепи. Правила Кирхгофа.
Узлами цепи будем именовать точки, в каких сходится более 3-х проводников цепи (рис.4).
1-ое правило Кирхгофа: алгебраическая сумма токов сходящихся в узле равна нулю:
При всем этом следует соблюдать следующее правило символов: токи приходящие к узлу считать положительными, уходящие — отрицательными.
2-ое правило Кирхгофа: алгебраическая сумма произведений токов на сопротивления в ветвях замкнутого контура равна алгебраической сумме ЭДС, встречающихся в этом контуре:
При всем этом следует придерживаться правила символов: токи, идущие вдоль избранного нами направления обхода (к примеру по часовой стрелке), числятся положительными, а идущие против направления обхода — отрицательными. Соответственно этому ЭДС которые действуют по избранному направлению обхода в контуре числятся положительными.
ЭЛЕКТРОМАГНЕТИЗМ
Магнитное поле.
Магнитное поле порождается перемещающимися зарядами. Магнитное поле характеризуется при помощи вектора магнитной индукции . Полосы касательные к которым в каждой точке совпадают с направлением вектора магнитной индукции в этой точке именуются полосы магнитной индукции. Магнитная индукция измеряется в теслах: [B] = 1 тл. Направление линий магнитной индукции определяется правилом буравчика.
Правило буравчика: если поступательное движение буравчика совпадает с направлением тока, то направление вращения его рукояти даст направление магнитных линий напряженности (рис.5).
О величине вектора магнитной индукции судят по величине вращающего момента, испытываемого пробной рамкой при ее повороте в магнитном поле (рис.6) :
a — угол между векторами и ; — магнитный момент контура с током
— единичный вектор нормали к рамке, направление которого определяется по правилу буравчика (рис.7).
Величина магнитной находится в зависимости от параметров среды. Черта независимая от параметров среды именуется вектором напряженностью магнитного поля . Напряженность магнитного поля измеряется в амперах деленных на метр [H] = 1 а/м.
m0 = 4 p 10 -7 Гн/м — магнитная неизменная; m — магнитная проницаемость среды, для вакуума m = 1.
Дабы отыскать суммарную индуктивность либо напряженность создаваемую несколькими магнитными полями применяют принцип суперпозиции магнитных полей: магнитное поле, создаваемое несколькими источниками, равно векторной сумме напряженностей магнитных полей от каждого источника
Закон Био-Савара-Лапласа.
Магнитная индукция , создаваемое элементом тока на расстоянии от него, назад пропорционально квадрату расстояния и прямо пропорционально величине элемента тока и синусу угла a между векторами и (рис.8)
Дабы получить результирующий вектор для денного определенного варианта делается интегрирование. Ниже при
1.Магнитная индукция проводника с током (рис.9)
2.Магнитная индукция нескончаемо длинноватого проводника с током
3.Магнитная индукция в центре прямоугольного контура с током
a и b — длины сторон контура.
4.Магнитная индукция радиального контура с током на оси контура (рис.10)
— магнитный момент радиального витка стоком; S — площадь рамки стоком, R — радиус контура, h — расстояние от центра витка до рассматриваемой точки.
5.Магнитная индукция радиального контура с током на оси контура
6.Магнитная индукция соленоида. Соленоидом именуется цилиндрическая катушка стоком состоящая из огромного числа витков проволоки, которые образуют винтообразную линию.
n – число витков соленоида на единицу длины.
7.Магнитная индукция нескончаемо длинноватого соленоида.
Силы Лоренца и Ампера
На частичку с электрическим зарядом Q, перемещающуюся в магнитном поле со скоростью v, действует сила Лоренца.
Направление силы Лоренца действующей на положительно заряженную частичку определяется по правилу левой руки: если расположить ладонь левой руки так, дабы полосы магнитной индукции входили в ладонь, а четыре вытянутых пальца совпадали с направлением движения частички , то отставленный большой палец укажет направление силы Лоренца, действующей на заряженную частичку в магнитном поле (рис.12,рис.13). Если частичка заряжена негативно, то сила Лоренца равна по модулю, но обратна по направлению силе действующей на положительную частичку (рис.13).
Если на заряженную частичку действует не только лишь магнитное поле с индукцией , но и электрическое поле с напряженностью , то результирующая сила равна
Силу именуют обобщенной силой Лоренца.
На проводник с электрическим током, находящийся в магнитном поле, действует сила Ампера. На элемент длины dl проводника с током силой I, находящегося в магнитном поле с индукцией B действует сила ампера dFА
На проводник длины l действует сила Ампера FА
a — угол между направлением тока в проводнике и вектором (рис.14).
Направление силы FA можно отыскать по правилу левой руки: если расположить ладонь левой руки так, дабы полосы магнитной индукции входили в ладонь, а четыре вытянутых пальца совпадали с направлением электрического тока в проводнике, то отставленный большой палец укажет направление силы Ампера, действующей на проводник в магнитном поле (рис.15).
Если в магнитное поле поместить рамку с током, то под действием пары сил рамка будет стремится оборотиться так, дабы ее нормаль , а поэтому и магнитный момент совпадали по направлению с вектором индукции поля (рис.16).
Два проводника с током делают собственные магнитные поля, при всем этом если токи текут в обратных направлениях, то проводники отталкиваются, если в одинаковом, то притягиваюбтся.
Проводник с током, помещенный в магнитное поле, испытывает пондемоторную силу, обусловленную силами Ампера. При перемещении проводника поле с током поле совершает работу. Разглядим линейный проводник длиной l с током I, перемещающийся в однородном магнитном поле (рис.17)
— площадь очерчиваемая проводником при его перемещении в магнитном поле, — магнитный поток пронизывающий эту площадь.
Если в переменном в пространстве (магнитная индукция поля изменяется от точки к точке) магнитном поле перемещается замкнутый контур с током, т.е. его площадь при перемещении не меняется, то при перемещении будет изменяться магнитный поток через контур. Такая ситуация вероятна, к примеру, при удалении либо приближении контура к неизменному магниту либо при вращении контура в неизменном магнитном поле. При всем этом силами Ампера также будет совершаться работа, определяемая по той же формуле
В этом случае
Если в магнитном поле перемещается замкнутый контур, имеющий N витков, а магнитный поток через любой из витков равен DΦ, тогда работа сил Ампера равна
Y — полный магнитный поток, сцепленный со всеми N витками, именуемый потокосцеплением; I – ток индукции, L – коэффициент самоиндукции (индуктивность).
Закон ома для цепи содержащей эдс
Формулы, применяемые на уроках физики в 10-11 классах «Закон Ома для всей цепи. Расчет электрических цепей» для подготовки к ЕГЭ по физике.
Смотрите также другие конспекты по решению задач:
Закон Ома для всей цепи.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задачка № 1. Вольтметр, присоединенный к лампочке, указывает U = 4 В, а амперметр — I = 2 А (рис. 6-10). Чему равно внутреннее сопротивление r источника тока, к которому эта лампочка присоединена, если ЭДС источника ε = 5 В?
Примечание: если в условии задачи ничего не сказано о сопротивлении амперметра, то этим сопротивлением можно пренебречь, а если ничего не сказано о сопротивлении вольтметра, то его следует считать нескончаемо огромным, а силу тока, текущего через вольтметр, равной нулю.
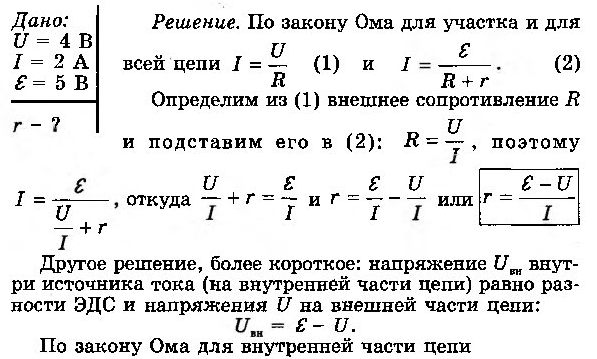
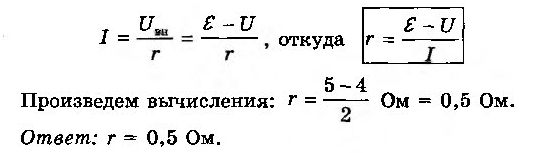
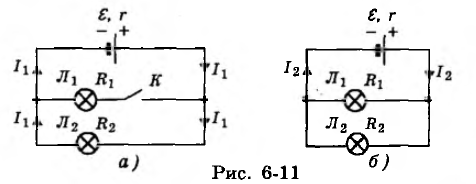
Задачка № 2. Дана схема (рис. 6-11, а). Во сколько раз поменяется сила тока, текущего в неразветвленной части цепи, и напряжение на полюсах источника тока, если ключ К замкнуть? Сопротивление лампы Л2 в два раза больше сопротивления лампы Л1, а внутреннее сопротивление источника тока в 10 раз меньше сопротивления лампы Л1.
Глядеть решение и ответ



Задачка № 3. В резисторе сопротивлением R = 5 Ом сила тока I = 0,2 А. Резистор присоединен к источнику тока с ЭДС ε = 2 В. Отыскать силу тока недлинного замыкания Iк.з.
Глядеть решение и ответ

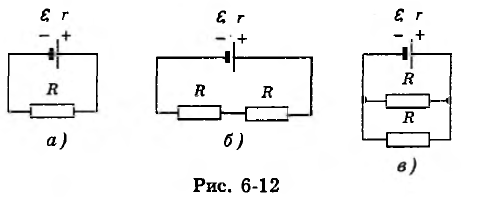
Задачка № 4. Вольтметр, присоединенный к полюсам источника тока при разомкнутой наружной цепи, показал U1 = 8 В. Когда же цепь замкнули на некоторый резистор (рис. 6-12, а), вольтметр показал U2 = 5 В. Что покажет этот вольтметр, если последовательно к этому резистору подключить очередной таковой же (рис. 6-12, б) ? Что покажет этот вольтметр, если 2-ой резистор присоединить к первому параллельно (рис. 6-12, в)?
Глядеть решение и ответ


Задачка № 5. Цепь питается от источника тока с ЭДС ε = 4 В и внутреннем сопротивлением г = 0,2 Ом. Выстроить график зависимости силы тока I в цепи и напряжения U на полюсах источника тока от наружного сопротивления R.
Глядеть решение и ответ


Задачка № 6. Амперметр, будучи накоротко присоединен к гальваническому элементу с ЭДС ε = 2 В и внутренним сопротивлением r = 0,2 Ом, показал ток силой I1 = 3 А . Какую силу тока I2 покажет этот амперметр, если его зашунтировать сопротивлением Rш = 0,1 Ом?
Глядеть решение и ответ


Задачка № 7. Дана схема (рис. 6-16). Емкости конденсаторов С1, С2 и ЭДС источника тока ε известны. Понятно также, что ток недлинного замыкания Iк.з. этого источника втрое превосходит ток I, текущий в этой цепи. Отыскать напряженности Е1 и Е2 полей в конденсаторах, если расстояния между их обкладками равны d.
Глядеть решение и ответ


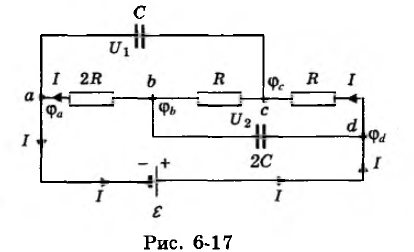
Задачка № 8. Дана схема (рис. 6-17). Известны емкости С и 2С конденсаторов, сопротивления R и 2R проводников и ЭДС источника тока ε. Внутренним сопротивлением источника тока можно пренебречь (г = 0). Найти напряжения U1 и U2 на конденсаторах и заряды q1 и q2 этих конденсаторов.
Глядеть решение и ответ

Задачка № 9. Имеется N одинаковых источников тока, которые соединяют поначалу последовательно, потом параллельно, подключая всякий раз к одному и тому же наружному сопротивлению R. Внутреннее сопротивление каждого источника r. Во сколько раз при всем этом меняется напряжение на наружной части цепи?
Глядеть решение и ответ

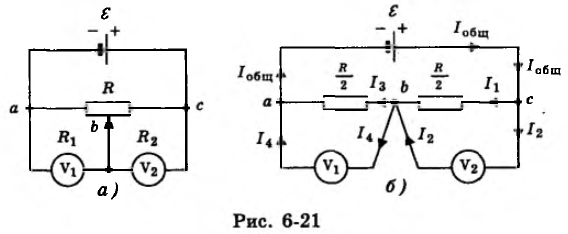
Задачка № 10. Электрическая цепь состоит из источника тока с ЭДС ε = 180 В и потенциометра сопротивлением R = 5 кОм. Ползунок потенциометра стоит в центре устройства (рис. 6-21, а). Отыскать показания вольтметров U1 и U2, присоединенных к потенциометру, если их сопротивления R1 = 6 кОм и R2 = 4 кОм. Внутренним сопротивлением r источника тока пренебречь.
Глядеть решение и ответ


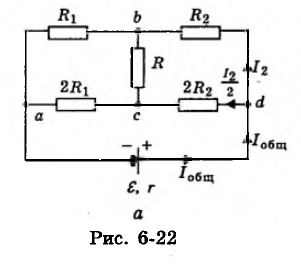
Задачка № 11. Дана схема, изображенная на рис. 6-22, а. Сопротивления R1, R2 и R известны. Известны также ЭДС источника тока ε и его внутреннее сопротивление r. Отыскать силу тока I2 в сопротивлении R2.
Глядеть решение и ответ


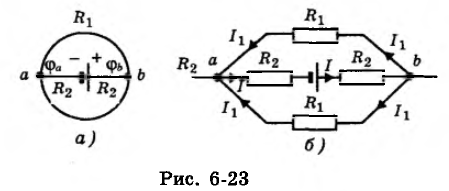
Задачка № 12. Проволока из нихрома образует кольцо поперечником D = 2 м (рис. 6-23, а). В центре кольца помещен источник тока с ε = 2В и внутренним сопротивлением r = 1,5 Ом, соединенный в точках а и b с кольцом таковой же проволокой. Отыскать разность потенциалов φb – φа между точками b и а. Удельное сопротивление нихрома р = 1,1 мкОм•м, площадь поперечного сечения проволоки S = 1 мм 2 .
Глядеть решение и ответ


Это конспект по теме «Закон Ома для всей цепи. ЗАДАЧИ на ЕГЭ». Изберите последующие деяния: