В § 2.3 были выведены соотношения, связывающие амплитуды переменных токов и напряжений на резисторе, конденсаторе и катушке индуктивности: R I R = U R ; 1 ω C I C = U C ; ω L I L = U L .
Эти соотношения во виду напоминают закон Ома для участка цепи неизменного тока, но только сейчас в них входят не значения неизменных токов и напряжений на участке цепи, а амплитудные значения переменных токов и напряжений.
Соотношения (*) выражают закон Ома для участка цепи переменного тока, содержащего один из частей R, L и C. Физические величины R, 1 ω C и ωL именуются активным сопротивлением резистора, емкостным сопротивлением конденсатора и индуктивным сопротивлением катушки.
При протекании переменного тока по участку цепи электромагнитное поле совершает работу, и в цепи выделяется джоулево тепло. Моментальная мощность в цепи переменного тока равна произведению моментальных значений тока и напряжения: p = J ċ u. Практический энтузиазм представляет среднее за период переменного тока значение мощности P = P ср = I 0 U 0 cos ω t cos ( ω t + φ ) ¯ .
Тут I0 и U0 – амплитудные значения тока и напряжения на данном участке цепи, φ – фазовый сдвиг между током и напряжением. Черта значит символ усреднения. Если участок цепи содержит только резистор с сопротивлением R, то фазовый сдвиг φ = 0: P R = I R U R cos 2 ω t ¯ = I R U R 2 = I R 2 R 2 .
Для того, дабы это выражение по виду совпадало с формулой для мощности неизменного тока, вводятся понятия действующих либо действенных значений силы тока и напряжения: I д = I 0 2 ; U д = U 0 2 .
Средняя мощность переменного тока на участке цепи, содержащем резистор, равна P R = I д U д .
Если участок цепи содержит только конденсатор емкости C, то фазовый сдвиг между током и напряжением φ = π 2 . Потому P C = I C U C cos ω t cos ( ω t + π 2 ) ¯ = I C U C cos ω t ( — sin ω t ) ¯ = 0.
Аналогично можно показать, что PL = 0.
Таким макаром, мощность в цепи переменного тока выделяется лишь на активном сопротивлении. Средняя мощность переменного тока на конденсаторе и катушке индуктивности равна нулю.
Разглядим сейчас электрическую цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки. Цепь подключена к источнику переменного тока частоты ω. На всех последовательно соединенных участках цепи протекает один и тот же ток. Между напряжением наружного источника e (t) и током J (t) появляется фазовый сдвиг на некоторый угол φ. Потому можно записать J (t) = I0 cos ωt; e (t) = ℰ0 cos (ωt + φ).
Такая запись моментальных значений тока и напряжения соответствует построениям на векторной диаграмме (рис. 2.3.2). Средняя мощность, развиваемая источником переменного тока, равна P = I 0 ℰ 0 cos ω t cos ( ω t + φ ) ¯ = I 0 ℰ 0 2 cos φ = I д ℰ д cos φ .
Как видно из векторной диаграммы, UR = ℰ0 · cos φ, потому P = I 0 U R 2 . Поэтому, вся мощность, развиваемая источником, выделяется в виде джоулева тепла на резисторе, что подтверждает изготовленный ранее вывод.
В § 2.3 было выведено соотношение между амплитудами тока I0 и напряжения ℰ0 для последовательной RLC-цепи: I 0 = ℰ 0 R 2 + ( ω L — 1 ω C ) 2 .
Величину Z = R 2 + ( ω L — 1 ω C ) 2 именуют полным сопротивлением цепи переменного тока. Формулу, выражающую связь между амплитудными значениями тока и напряжения в цепи, можно записать в виде ZI0 = ℰ0.
Это соотношение именуют законом Ома для цепи переменного тока. Формулы (*), приведенные сначала этого параграфа, выражают личные случаи закона Ома (**).
Понятие полного сопротивления играет важную роль при расчетах цепей переменного тока. Для определения полного сопротивления цепи в почти всех случаях комфортно применять приятный способ векторных диаграмм. Разглядим в качестве примера параллельный RLC-контур, присоединенный к наружному источнику переменного тока (рис. 2.4.1).
Параллельный RLC-контур
При построении векторной диаграммы следует учитывать, что при параллельном соединении напряжение на всех элементах R, C и L одно и то же и равно напряжению наружного источника. Токи, текущие в различных ветвях цепи, отличаются не только лишь по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Потому полное сопротивление цепи нельзя вычислить по законам параллельного соединения цепей неизменного тока. Векторная диаграмма для параллельного RLC-контура изображена на рис. 2.4.2.
Векторная диаграмма для параллельного RLC-контура
Из диаграммы следует: I 0 = ℰ 0 ( 1 R ) 2 + ( ω L — 1 ω C ) 2 .
Потому полное сопротивление параллельного RLC-контура выражается соотношением Z = 1 ( 1 R ) 2 + ( ω L — 1 ω C ) 2 .
При параллельном резонансе (ω 2 = 1 / LC) полное сопротивление цепи воспринимает наибольшее значение, равное активному сопротивлению резистора: Z = Zmax = R.
Фазовый сдвиг φ между током и напряжением при параллельном резонансе равен нулю.
Особенности закона Ома для переменного тока
1-ая и, может быть, важнейшая связь между током, напряжением и сопротивлением именуется законом Ома, который был открыт Георгом Саймоном и размещен в статье 1827 года «Математически исследованная гальваническая цепь».
Формулировка закона для последовательной цепи переменного тока
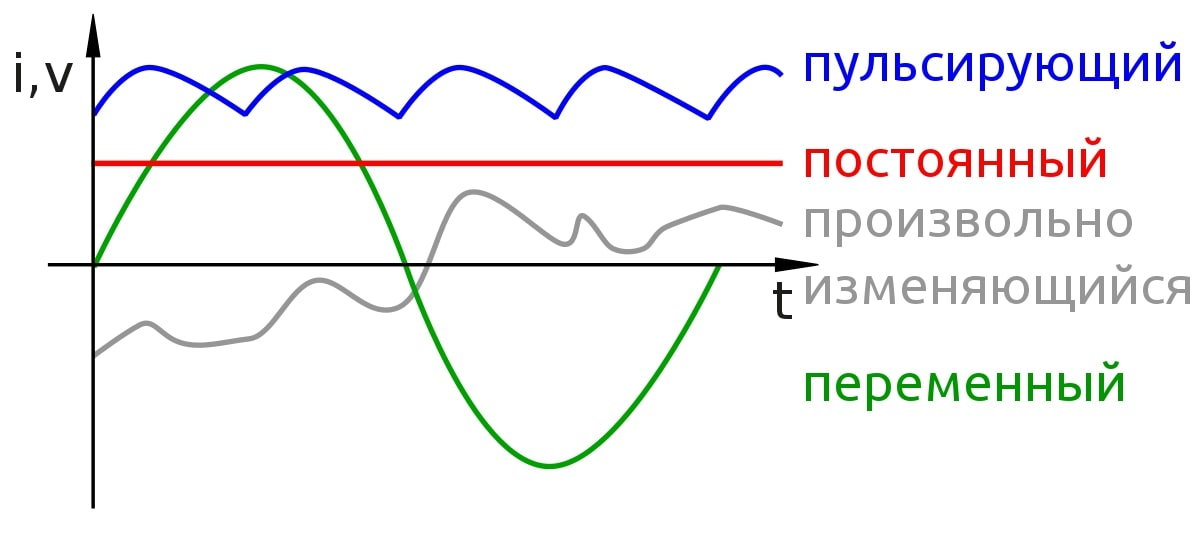
Переменный ток обрисовывает поток заряда, который временами меняет направление. В итоге уровень напряжения также меняется вкупе с током. AC применяется для подачи электроэнергии в дома, офисные строения и т. д.
AC может быть произведен с внедрением устройства — токовый генератор. Это устройство представляет собой особенный тип электрического генератора, созданный для выработки.
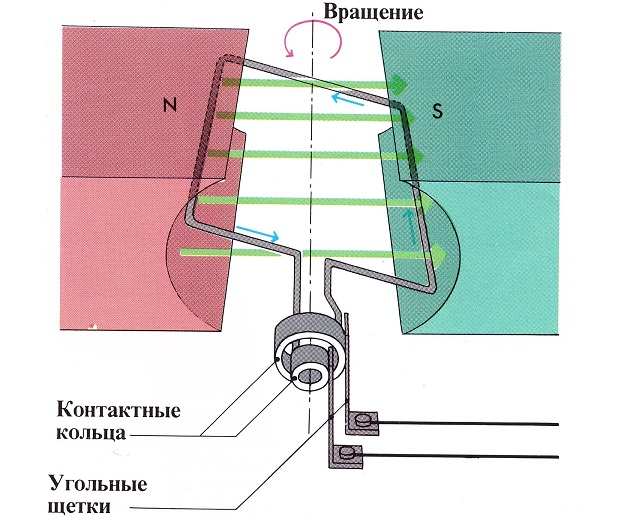
Генерация
Петля провода крутится снутри магнитного поля, которое индуцирует течение вдоль провода. Вращение проволоки может происходить из любого количества средств: ветряная турбина, паровая турбина, проточная вода и т.д. Так как провод крутится и временами заходит в другую магнитную полярность, напряжение и ток на проводе чередуются.
Для генерации переменного потока электронов в наборе водопроводных труб подключается механический кривошип к поршню, который перемещает воду в трубах назад-вперед.
Направьте внимание: зажатый участок трубы как и раньше обеспечивает сопротивление сгустку воды независимо от направления потока.
Если сила и ток чередуются, разряд же может быть различных форм. Если подключить осциллограф к цепи и выстроить график, со временем можно узреть несколько разных форм сигнала.

Волны
Более распространенным типом потока электронов является синусоида. В большинстве домов и кабинетов поток имеет колебательную интенсивность, которая делает синусоидальную волну, как на рисунке выше.
Другие распространенные формы разряда содержат в себе прямоугольную и треугольную волну.
Квадратные волны нередко применяются в цифровой и коммутационной электронике для проверки их работы.
Треугольные волны находятся в синтезе звука и полезны для тестирования линейной электроники, таковой как усилители.
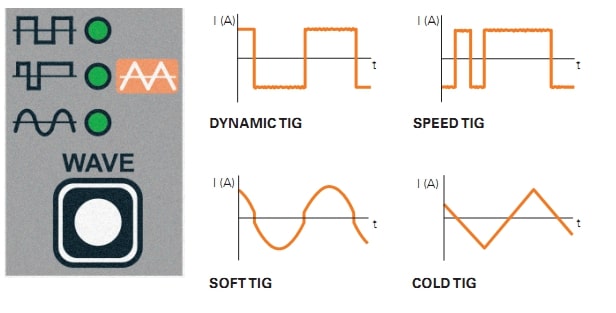
Прямоугольная и треугольная волна
Закон Ома для мощности переменного тока
Узнаваемый треугольник закона Ома, применяемый для цепей неизменного потока электронов, может употребляться только при переменном разряде, если нагрузка является чисто резистивной. Но большая часть систем содержат последовательные либо параллельные композиции сопротивления, емкости и индуктивности. Это приводит к несоответствию напряжения и разряда, и нагрузка становится сложной. В чисто емкостных системах форма волны разряда опережает форму волны напряжения, тогда как в индуктивных цепях интенсивность опережает разряд. В цепях, содержащих как катушки индуктивности, так и конденсаторы, форма сигнала не будет синфазной, не считая как в резонансе. Общим термином для сопротивления является полное сопротивление и обозначается эмблемой Z. Треугольник полного сопротивления показан ниже:
Для вас это будет любопытно Определение тока либо напряжения в розетке
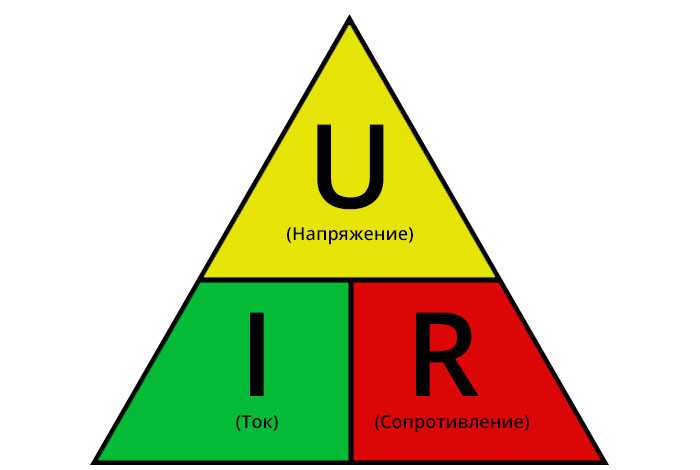
Треугольник
Треугольник применяется точно так же, за некоторым исключением.
Следует отметить: при измерении напряжения либо разряда измеритель будет демонстрировать только правильные значения в ограниченном спектре частот. Как правило это справедливо для неизменного тока до 400 Гц, но это можно выяснить, проверив спецификации устройства.
Для цепей, в каких напряжение и ток находятся исключительно в фазе, может употребляться такая радиальная диаграмма.
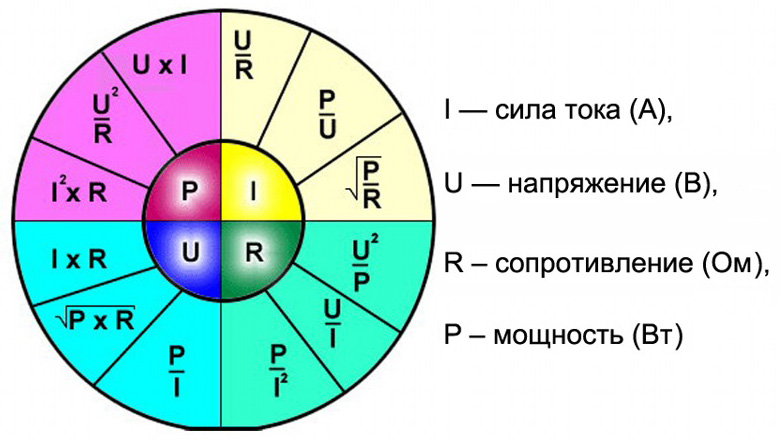
Диаграмма
Закон Ома для участка цепи
Неизменный ток (DC) осознать малость легче. Заместо того, дабы колебаться вспять и вперед, разряд обеспечивает неизменное напряжение.
DC может быть сгенерирован несколькими методами:
- при помощи генератора, который обустроен устройством, именуемым «коммутатор», может создавать поток электронов;
- с внедрением устройства под заглавием «выпрямитель», который конвертирует переменный разряд в неизменный;
- батареи обеспечивают неизменное движение, которое генерируется в итоге хим реакции снутри батареи.
DC определяется как «однонаправленный» поток (течет исключительно в одном направлении). Напряжение и разряд могут изменяться, пока направление потока не поменяется. Для упрощения можно представить, что напряжение является неизменным. К примеру, подразумевается, что батарея АА обеспечивает 1,5 В, что в математических определениях можно обрисовать так: V(t)=1,5V
Если выстроить график со временем, будет видно неизменное напряжение:
График
Что это означает? Это значит, что можно рассчитывать на большая часть источников неизменного разряда для обеспечения напряжения во времени. В реальности батарея будет равномерно терять заряд, а это значит, что при использовании батареи напряжение будет падать. Поэтому, можно представить, что оно повсевременно.
Формула
Закон Ома не может быть использован к цепям переменного потока электронов, так как он не учитывает реактивное сопротивление, которое всегда находится в таких цепях. Но, меняя закон Ома, который учитывает воздействие реактивного сопротивления, выходит общий закон Ома для последовательной цепи переменного тока, применимый к цепям этого движения (закон Ома для неизменного и переменного тока). Так как полное сопротивление Z представляет собой совокупное сопротивление всех реактивных сопротивлений, то общий закон Ома для переменного тока: I=E/Z
Для вас это будет любопытно Подключение к сетям
Эта общая модификация применяется к переменному сгустку электронов, протекающему в хоть какой цепи, и хоть какое из значений может быть найдено из уравнения, если другие известны.
Использование закона
Если технические спецы во время тестирования стандартных характеристик разрядов найдут, что обыденные значения не регистрируются на их цифровых мультиметрах либо измерителях токовых клещей, то они могут применять закон Ома, дабы найти, какая часть цепи дает сбой, и исходя из этого найти, в чем может заключаться неувязка.
Активное, емкостное и индуктивное сопротивление. Закон Ома для цепей переменного тока
ГОСТ
Активное сопротивление
Пусть источник переменного тока включен в цепь, в какой индуктивностью и емкостью можно пренебречь. Переменный ток меняется в согласовании с законом:
Тогда, если применить к участку цепи ($а R в$) (рис.1) закон Ома получим:
где $U$ — напряжение на концах участка. Разность фаз между током и напряжением равна нулю. Амплитудное значение напряжения ($U_m$) равно:
где коэффициент $R$ — именуется активным сопротивлением. Наличие активного сопротивления в цепи всегда приводит к выделению тепла.
Ёмкостное сопротивление
Допустим, что в участок цепи включен конденсатор емкости $С$, а $R=0$ и $L=0$. Будем считать силу тока ($I$) положительной, если она имеет направление, которое обозначено на рис. 2. Пусть заряд на конденсаторе равен $q$.
Мы можем применять следующие соотношения:
Если $I(t)$ определена уравнением (1), то заряд выражен как:
где $q_0$ случайный неизменный заряд конденсатора, который не связан с колебаниями тока, потому можем допустить, что $q_0=0.$ Получим напряжение равно:
Формула (6) указывает, что на конденсаторе колебания напряжения отстают от колебаний силы тока по фазе на $\frac<\pi >.$ Амплитуда напряжения на емкости равна:
Величину $X_C=\frac<\omega C>$ именуют реактивным емкостным сопротивлением (емкостным сопротивлением, кажущимся сопротивлением емкости). Если ток неизменный, то $X_C=\infty $. Это означает, что неизменный ток не течет через конденсатор. Из определения емкостного сопротивления видно, что при огромных частотах колебаний, малые емкости являются маленькими сопротивлениями переменного тока.
Готовые работы на аналогичную тему
Получить выполненную работу либо консультацию спеца по вашему учебному проекту Выяснить цена
Индуктивное сопротивление
Пусть участок цепи имеет только индуктивность (рис.3). Будем считать $I>0$, если ток ориентирован от $а$ к $в$.
Если в катушке течет ток, то в индуктивности возникает ЭДС самоиндукции, поэтому, закон Ома воспримет вид:
По условию $R=0. \mathcal E$ самоиндукции можно выразить как:
Из выражений (8), (9) следует, что:
Амплитуда напряжения в этом случае равна:
где $X_L-\ $индуктивное сопротивление (кажущееся сопротивление индуктивности).
Закон Ома для цепей переменного тока
именуют полным электросопротивлением, либо импедансом, время от времени именуют законом Ома для переменного тока. Но нужно держать в голове, что формула (12) относится к амплитудам тока и напряжения, а не моментальным их значениям.
Задание: Чему равно действующее значение силы тока в цепи. Цепь переменного тока состоит из последовательно соединенных: конденсатора емкостью $C$, катушки индуктивности $L$, активного сопротивления $R$. На зажимы цепи подается напряжение действующее напряжение $U$ частота которого $\nu$.
Решение:
Так как все элементы цепи соединены последовательно, то сила тока во всех элементах одинакова.
Амплитудное значение силы тока выражается «законом Ома для переменного тока»:
оно связано с действующим значением силы тока как:
В критериях задачи мы имеем действующее значение напряжения $U$, нам в формуле (1.1) нужна амплитуда напряжения, используя формулу:
Подставим в формулу (1.2) формулы (1.1) и (1.3), получим:
где $\omega =2\pi \nu .$
Задание: Используя условия задачи в первом примере, найдите действующие значения напряжений на катушке индуктивности ($U_L$), сопротивлении ($U_R$), конденсаторе ($U_C$).
Решение:
Используем итог примера 1. Напряжение на катушке индуктивности выражается формулой:






