В прошлом параграфе было установлено, что упорядоченное движение свободных заряженных частиц в проводнике вызывается электрическим полем.
В случае неизменного тока это поле представляет собой возможное стационарное поле. Разность потенциалов между концами проводника определяет силу тока в нем: I = F(φ1 — φ2). Эта зависимость именуется вольт-амперной чертой проводника. Установление ее играет главную роль при исследовании явлений, связанных с прохождением тока.
Закон Ома
Более обычной вид имеет вольт-амперная черта железных проводников и смесей электролитов.
В первый раз (для металлов) ее установил германский ученый Георг Ом в 1826 г., потому зависимость силы тока от напряжения носит название закона Ома.
Георг Ом начал свои опыты по установлению зависимости между силой тока в проводнике и разностью потенциалов на его концах в 20-х гг. XIX в. Ом экспериментировал с проволоками разной длины, разной толщины (будучи отпрыском слесаря, он знал, как растягивать железную проволоку разной толщины для собственных опытов), сделанными из различных металлов, и даже проводил опыты при различной температуре, варьируя каждый фактор попеременно как все истинные Исследователи. Батареи в те времена были еще очень слабенькие, они делали непостоянный ток. Потому Ом воспользовался в качестве источника тока термопарой*, один из спаев которой был помещен в пламя. Он использовал твердый магнитный амперметр, а разности потенциалов изменял методом конфигурации температуры либо числа термоспаев.
Теоретические выводы и экспериментальные результаты были изложены Омом в размещенной в 1826 г. книжке. Но они не нап1ли осознания. Способ грубого экспериментирования по заблаговременно намеченному плану казался малопривлекательным в эру увлечения философией. Признание пришло только 23 года спустя после выхода книжки. В 1849 г. Ом получил должность доктора Мюнхенского института.
На рисунке 2.12 изображен участок цепи 1, 2. Условимся считать положительным на правление слева вправо. Тогда напряжение (разность потенциалов) на рассматриваемом участке равно U = φ1 — φ2, где φ1 — потенциал в точке 1 (сначала участка), а φ2 — потенциал в точке 2 (в конце участка). Если φ1 > φ2, то U > 0 и ток течет в направлении от точки 1 к точке 2, так как в эту сторону ориентированы полосы напряженности электрического поля снутри проводника. Поэтому, и сила тока I тоже положительна (I > 0).
Ом экспериментально установил прямую пропорциональную зависимость между силой тока и напряжением;
Эта зависимость справедлива как для металлов, так и для смесей (расплавов) электролитов.
Зависимость (2.4.1) можно записать в виде равенства

Это равенство и именуется законом Ома для участка цепи. Тут G — коэффициент пропорциональности, значение которого не находится в зависимости от напряжения на концах проводника и от силы тока в нем. Коэффициент пропорциональности находится в зависимости от самого проводника и потому является его чертой. Этот коэффициент именуют проводимостью проводника.
Таким макаром, закон Ома для участка цепи содержит испытанное на опыте утверждение о том, что сила тока прямо пропорциональна разности потенциалов; сразу он содержит определение проводимости проводника. Закон Ома можно сконструировать так: сила тока в проводнике прямопропорциональна проводимости проводника и напряжению (разности потенциалов) на его концах.
Величину, оборотную проводимости проводника
именуют электрическим сопротивлением либо просто сопротивлением. Поэтому, сопротивление тоже является чертой проводника. Исторически сложилось, что конкретно сопротивление считается основной электрической чертой проводника.
Если проводимость G выразить через сопротивление , то формула (2.4.2) воспримет вид:
Выражение (2.4.3) представляет собой другую формулировку закона Ома для участка цепи: сила тока в цепи прямо пропорциональна напряжению на ее участке и назад пропорциональна сопротивлению этого участка.
Следует подразумевать, что закон Ома в форме (2.4.3) либо (2.4.2) справедлив только для участка цепи, в каком нет источника тока**.
Закон Ома имеет очень ординарную форму, но обосновать экспериментально его справедливость достаточно тяжело. Дело в том, что разность потенциалов на участке железного проводника даже при большой силе тока мала, так как не много сопротивление проводника. Электрометр, о котором шла речь в § 1,21, непригоден для измерения настолько малых напряжений: его чувствительность очень мала. Нужен несоизмеримо более чувствительный устройство, к примеру электростатический вольтметр. Использование же обыденных устройств для измерения напряжения — вольтметров — основано на использовании закона Ома. Принцип деяния вольтметра таковой же, как и амперметра: угол поворота стрелки устройства пропорционален силе тока. Сила тока, проходящ,его по вольтметру, согласно закону Ома, определяется напряжением между точками цепи, к которым он подключен. Потому, зная сопротивление вольтметра, можно по силе тока найти напряжение. На практике устройство сходу градуируют в единицах напряжения.
Закон Ома является эмпирическим, а не базовым законом природы. Но он осуществляется очень точно в широких границах для металлов. В данном случае закон Ома фактически справедлив для всех неизменных напряжений, при применении которых проводник не плавится.
Наименее широки рамки использования закона Ома для смесей (и расплавов) электролитов и сильно ионизованных газов — плазмы. При огромных напряжениях он перестает производиться.
Сопротивление
Закон Ома определяет новейшую электрическую характеристику проводника — сопротивление. От этой величины зависит сила тока в проводнике при данном напряжении. Сопротивление проводника представляет собой вроде бы меру противодействия проводника установлению в нем электрического тока. Сопротивление проводника можно найти при помощи закона Ома (2.4.3):
Сопротивление равно отношению разности потенциалов на концах проводника к силе тока в нем.
Единицы сопротивления
В абсолютной системе единиц за единицу сопротивления принимают сопротивление проводника, в каком при напряжении на его концах в одну электростатическую единицу напряжения сила тока равна одной электростатической единице силы тока:
Единицей сопротивления в СИ является Ом. 1 Ом — сопротивление проводника, в каком при напряжении на его концах в 1 В сила тока в нем равна 1 А.
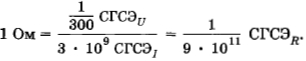
Заметим, что термин «сопротивление» употребляют в 2-ух смыслах:
во-1-х, электрическое сопротивление — это величина, определяющая силу тока при данном напряжении. В этом смысле, к примеру, молвят: лампа накаливания обладает сопротивлением 400 Ом либо провод имеет сопротивление 0,5 Ом;
во-2-х, резистором (либо сопротивлением) именуют устройство, созданное для включения в электрическую цепь с целью регулирования, уменьшения либо ограничения тока цепи. Таким устройством может служить, к примеру, реостат для регулирования силы тока в цепи методом конфигурации сопротивления. Резисторы обширно используются в радиоприемниках, телеках и других устройствах. Условное обозначение резистора показано на рисунке 2.12.
Удельное сопротивление
Сопротивление находится в зависимости от материала проводника и его геометрических размеров. Опыт указывает, что при постоянной температуре сопротивление однородного проводника неизменного оечения прямо пропорционально его длине l и назад пропорционально площади S поперечного сечения проводника:
Введем коэффициент пропорциональности и запишем последнюю зависимость в виде равенства

Коэффициент пропорциональности ρ численно равен сопротивлению проводника единичной длины и единичного поперечного сечения и именуется удельным сопротивлением проводника. Удельное сопротивление находится в зависимости от рода вещества и его состояния (прежде всего, от температуры).
Из формулы (2.4.6) находим:
Отсюда видно, что единицей удельного сопротивления в СИ является
Ом-метр равен удельному сопротивлению проводника площадью поперечного сечения 1 м 2 и длиной 1 м, имеющего сопротивление 1 Ом.
Удельное сопротивление металлов не много. К примеру, удельное сопротивление обыкновенной технической меди при 20 °С равно 1,72 • 10 -8 Ом • м. Механическая и термообработка приметно оказывает влияние на электрическое сопротивление металлов. Так, после холодной протяжки удельное сопротивление медной проволоки растет до 1,77 • 10 -8 Ом • м.
Еще поразительнее зависимость сопротивления от наличия жалких примесей. Кропотливая чистка уменьшает удельное сопротивление меди при температуре 20 °С до 1,69 • 10 -8 Ом • м. Но довольно добавить к меди 1% марганца, дабы удельное сопротивление ее возросло до 4,8 • 10 -8 Ом • м, т. е. практически в 3 раза! Приблизительно так же оказывают влияние на удельное сопротивление добавки железа, кобальта, иридия и др.
У сплавов, содержащих примеси в значимом количестве, сопротивление очень велико. Удельное сопротивление этих сплавов в пару раз больше, чем у каждой из составных частей. Так, константан, состоящий из 60% меди и 40% никеля, имеет удельное сопротивление 4,4 • 10 -7 Ом • м, в то время как у незапятанной меди оно равно 1,7 • 10 -8 Ом • м, а у никеля — 7,2 • 10 -8 Ом • м***.
«Королем» схожих сплавов можно именовать нихром, удельное сопротивление которого около 10 -6 Ом • м. Недаром он отыскал такое обширное использование в нагревательных устройствах.
Диэлектрики владеют очень огромным, но конечным удельным сопротивлением. Так, удельное сопротивление фарфора 10 13 Ом • м.
В таблице 3 приведены примеры значений удельного сопротивления некоторых веществ.
17.3. Закон Ома для участка цепи. Сопротивление проводников
Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному железному проводнику, пропорциональна падению напряжения U на проводнике:
Однородным именуется участок цепи, в каком не действуют посторонние силы.
Величина R именуется электрическим сопротивлением проводника. Единицей сопротивления служит Ом, равный сопротивлению такового проводника, в каком при напряжении 1В течет ток в 1 А.
Величина сопротивления находится в зависимости от формы и размеров проводника, также от параметров материала, из которого он изготовлен. Для однородного цилиндрического проводника .
где — длина проводника, S — площадь поперечного сечения, — зависящий от параметров материала коэффициент, именуемый удельным электрическим сопротивлением вещества.
Величина оборотная сопротивлению именуется проводимостью
Для большинства металлов удельное сопротивление вырастает с температурой примерно по линейному закону.
где — удельное сопротивление при 0°С, t — температура в градусах Цельсия, — неизменный коэффициент, численно равный приблизительно 1/273.Закон Ома можно записать в дифференциальной форме. Выделим в проводнике простый цилиндрический объем dV с образующими, dlпараллельными вектору плотности тока в данной точке (рис. 17.2). Через поперечное сечение dS цилиндра течет ток силой . Напряжение, приложенное к цилиндру, равно , где Е — напряженность поля в данном месте. Сопротивление цилиндра . Подставив эти значения в уравнение (17.5), получим
Носители заряда в каждой точке движутся в направлении вектора . Потому направления векторов и совпадают. Таким макаром, можно написать
17.4. Закон Ома в интегральной форме
Для хоть какой точки снутри проводника напряженность результирующего поля равна сумме напряженности поля кулоновских сил и поля посторониих сил . Подставляя в (17.6), получим
Умножим скалярно обе части на вектор , численно равный элементу длины проводника и направленный по касательной к проводнику в ту же сторону, что и вектор плотности тока
Так как скалярное произведение совпадающих по направлению векторов и , равно произведению их модулей, то это равенство можно переписать в виде
С учетом
Интегрируя по длине проводника от сечения 1 до некоторого сечения 2 и беря во внимание, что сила тока во всех сечениях проводника одинакова, получаем
Интеграл численно равен работе, совершаемой кулоновскими силами при перенесении единичного положительного заряда с точки 1 в точку 2. В электростатике было показано, что
Таким макаром, где и — значение потенциала в т.1 и т.2.
Интеграл, содержащий вектор напряженности поля, посторониих сил, представляет собой эдс , действующей на участке 1-2
равен сопротивлению участка цепи 1-2.
Подставляя (17.10), (17.9) и (17.8) в (17.7), совсем получим
Последнее уравнение выражает собой закон Ома в интегральной форме для участка цепи, содержащего эдс и формулируется следующим образом: падение напряжения на участке цепи равно сумме падений электрического потенциала на этом участке и эдс всех источников электроэнергии, включённых на участке.
При замкнутой наружной цепи сумма падений электрических потенциалов и эдс источника равна сумме падений напряжения на внутреннем сопротивлении источника и во всей наружной цепи где либо Отсюда