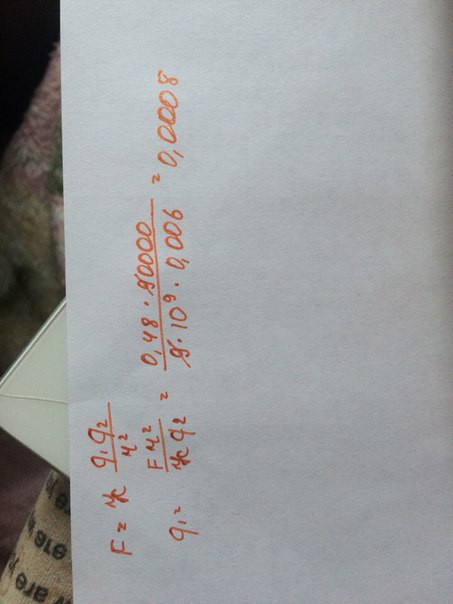Точечные заряды. Начало количественного исследования электромагнитных взаимодействий относится к концу XVIII в. В 1785 г. французский физик Шарль Кулон (1736—1806) экспериментально установил основной закон электростатики — закон взаимодействия 2-ух точечных недвижных заряженных тел либо частиц.
Точечные заряды — заряженные тела, размеры которых существенно меньше расстояния между ними.
Только для точечных зарядов понятие расстояния между зарядами имеет определённый смысл. Принципиально осознавать, что точечных зарядов в природе нет, это — физическая модель. Но если расстояние между телами во много раз больше их размеров, то ни форма, ни размеры заряженных тел не оказывают влияние на взаимодействие между ними. Силы взаимодействия заряженных тел зависят от параметров среды, в какой они находятся. При рассмотрении опытов Кулона мы будем считать, что электростатическое взаимодействие происходит или в вакууме, или в воздухе, воздействием которого на силы электростатического взаимодействия можно пренебречь.
Закон взаимодействия точечных недвижных зарядов — базовый физический закон, который мог быть установлен только опытным путём. Силы 1 взаимодействия оказались довольно значительны, и потому Кулону не пришлось использовать особо чувствительную аппаратуру.
1 Тут и в предстоящем ради сокращенности мы будем нередко заместо термина «модуль силы» применять термин «сила».
Опыты Кулона.
C помощью крутильных весов удалось установить, как ведут взаимодействие вместе мелкие заряженные шарики. Крутильные весы Кулона состоят из стеклянной палочки, подвешенной на узкой упругой проволочке 1 (рис. 9.8).
На одном конце палочки (коромысло весов) закреплён бузиновый золотой шарик 2, а на другом конце — противовес 3. Ещё один шарик 4 бездвижно закреплён на крышке весов. Вращением стержня 5 со стрелкой 7, на котором закреплена проволочка 1 с коромыслом, приводят шарики 2 и 4 в соприкосновение. Потом шарик 4 вынимают, заряжают его и опять опускают до соприкосновения с шариком 2. При всем этом часть заряда перебегает с шарика 4 на шарик 2, и они отталкиваются. Проволочка 1 закручивается на некоторый угол φ1 (рис. 9.9), который отсчитывается по нижней шкале 6 (см. рис. 9.8).
В итоге тестов Кулон нашел, что при уменьшении расстояния между шариками в 2 раза угол закручивания проволочки увеличивался в 4 раза. Во столько же раз увеличивался момент силы, так как при деформации кручения момент силы прямо пропорционален углу закручивания, а означает, и сила (плечо силы оставалось постоянным).
Отсюда следует принципиальный вывод: сила взаимодействия 2-ух заряженных шариков назад пропорциональна квадрату расстояния между ними:
Для определения зависимости силы электростатического взаимодействия от заряда шариков Кулон выдумал обычный и смышленый метод конфигурации заряда 1-го из шариков 2 . Для этого он соединял заряженный шарик с таким же, но незаряженным шариком.
2 В то время было нереально измерить заряд и не были установлены единицы заряда.
Согласно закону сохранения электрического заряда, полный заряд электрически изолированной системы шариков должен оставаться постоянным. Вот поэтому заряд в опытах Кулона распределялся поровну между шариками, что и уменьшало исследуемый заряд в 2, 4 и т. д. раз. Это позволило Кулону изучить электростатическое взаимодействие шариков с различными зарядами.
В итоге тестов было выяснено, что сила электростатического взаимодействия 2-ух точечных заряженных тел прямо пропорциональна произведению модулей зарядов шариков:
Закон Кулона. Кулоновские силы.
Опыты Кулона привели к установлению закона, напоминающего по форме закон глобального тяготения. Используя соотношения (1) и (2), сформулируем закон Кулона.
Сила взаимодействия 2-ух точечных недвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и назад пропорциональна квадрату расстояния между ними.
Эта сила ориентирована вдоль полосы, соединяющей эти заряды. Силы электростатического взаимодействия точечных недвижных зарядов нередко именуют кулоновскими. Если обозначить модули зарядов через ∣q1∣ и ∣q2∣, то закон Кулона можно записать в следующей форме:
Если все физические величины, входящие в формулу (3), выразить в единицах СИ, то наименование коэффициента пропорциональности k можно записать в следующем виде: H • м 2 ∕Kл 2 . Числовое значение коэффициента k находится опытным путём. Для вакуума с высочайшей степенью точности можно считать, что k = 9 ∙ 10 9 H • м 2 ∕Kл 2 .
Этот коэффициент связан с так именуемой электрической неизменной ε0:
Кулоновские силы приложены к заряженным телам и ориентированы вдоль прямой, соединяющей эти тела, т. е. эти силы являются центральными. Если точечные заряды являются одноимёнными (рис. 9.10, а), то силы 12 и 21 ориентированы в обратные стороны.
Если знаки зарядов различны, то действующие на эти заряды силы ориентированы навстречу друг дружке (рис. 9.10, б). По третьему закону Ньютона сила 12, действующая на заряд g1 со стороны заряда g2, равна по модулю и обратна по направлению силе 21, действующей на заряд g2 со стороны заряда g1.
Взаимодействие недвижных зарядов снутри диэлектрика.
Диэлектрики состоят из нейтральных в целом атомов либо молекул 3 . Электрически заряженные частички в нейтральном атоме связаны вместе и не могут, подобно свободным электронам, передвигаться по всему объёму тела. Пусть заряженные шарики помещены в однородный диэлектрик. Лучше применять водянистый диэлектрик (керосин, масло и т. д.), так как измерить силу взаимодействия заряженных тел снутри твёрдого диэлектрика тяжело из-за возникающих в нём упругих напряжений.
3 Тела, сделанные из диэлектриков, именуют изоляторами. Есть вещества, которые занимают среднее положение между проводниками и диэлектриками. Их именуют полупроводниками. О свойствах полупроводников будет поведано в курсе физики 11 класса.
Сила взаимодействия между зарядами в однородном диэлектрике, как указывает опыт, всегда меньше, чем в вакууме. Причём отношение модуля силы F0 взаимодействия зарядов в вакууме к модулю силы взаимодействия F этих же зарядов на том же расстоянии в среде не зависит ни от самих зарядов, ни от расстояния между ними. Оно определяется только качествами самой среды. Если обозначить это отношение через ε, то
Величину ε именуют диэлектрической проницаемостью среды.
Диэлектрическая проницаемость среды — это физическая величина, характеризующая электрические характеристики вещества и показывающая, во сколько раз сила взаимодействия зарядов в данной среде меньше силы их взаимодействия в вакууме.
Отметим, что ε — безразмерная величина, она всегда больше 1.
Закон Кулона для взаимодействия зарядов в среде может быть записан в виде:
Вопросы:
1. Что именуют точечным зарядом?
2. Опишите установку Кулона (см. рис. 9.8), при помощи которой был экспериментально открыт основной закон электростатики.
3. Сформулируйте закон Кулона и запишите его формулу.
4. Какие силы именуют кулоновскими? Как они ориентированы:
а) для разноимённо;
б) одноимённо заряженных тел?
5. Что указывает диэлектрическая проницаемость среды?
Вопросы для обсуждения:
1. Почему в опыте Кулона взаимодействующие заряды можно считать точечными?
2. Маятник изготовлен из эбонитового шарика, подвешенного на узкой нерастяжимой шёлковой нити. Шарик заряжен негативно. Как поменяется период колебаний маятника, если 2-ой, положительно заряженный шарик:
а) поднести снизу;
б) поместить в точке подвеса?
Пример решения задачи
Два одинаковых заряженных шарика, подвешенных на непроводящих нитях одинаковой длины, опускают в керосин. Какой должна быть плотность материала шариков, дабы угол расхождения нитей в воздухе и в керосине был один и тот же? Ответ приведите в г/см 3 .
Ответ: ρ = 1,6 г/см 3 .
Упражнения:
1. Во сколько раз нужно поменять расстояние между точечными недвижными зарядами при увеличении 1-го из них в 4 раза, дабы сила их электростатического взаимодействия осталась прежней?
2. Два одинаковых железных шарика имеют заряды q и -5q?. Шарики привели в соприкосновение и раздвинули на прежнее расстояние. Во сколько раз поменяется модуль силы электростатического взаимодействия между шариками?
3. Два шарика малых размеров с одинаковыми отрицательными зарядами размещены в вакууме на расстоянии r = 3 см друг от друга и отталкиваются с силой, модуль которой равен F = 2 • 10 -5 Н. Найдите число лишних электронов N на каждом шарике.
4. C какой по модулю кулоновской силой ведут взаимодействие заряды 4 нКл и 90 нКл на расстоянии 6 см:
5. C какой по модулю силой вели взаимодействие бы две капли воды на расстоянии 10 км, если б удалось передать одной из капель 2% всех электронов, содержащихся в другой капле массой 5 ∙ 10 -5 кг?
Закон Кулона и его полевая трактовка
ГОСТ
Историческая справка
Закон Кулона заходит в число главных экспериментальных фактов, находящихся в основании теории б электричестве. Этот закон для определения силы взаимодействия точечных зарядов $q_1\ $ и $q_2$, которые находятся на расстоянии $r$, имеет вид:
Этот закон установлен Ш. Кулоном в 1785 г. экспериментально. Кулон определял силы взаимодействия заряженных тел. Точность опытов была нехороший, только аналогии с силами тяготения отдала уверенность в том, что закон в виде (1) справедлив. С плодами опыта, обычно ассоциируют следствия из закона Кулона, и на этой базе делается вывод о точности и границах использования данного закона. 1-ая проверка закона была проведена Кавендишем за 13 лет до Кулона. Кавендиш работ не публиковал, но нужно отметить, что его способ был более четким, чем опыты Кулона. Позже опыты по проверке закона Кулона проводил Максвелл. Эти опыты подтвердили справедливость закона Кулона с большой точностью. В согласовании с современными представлениями электромагнитные взаимодействия осуществляются средством фотонов. Вследствие чего вопрос о справедливости закона Кулона сводится к вопросу о равенстве массы фотона нулю. Все частички владеют корпускулярными и волновыми качествами. Энергия фотона ($_=h\nu $) и $_=m_c^2$, где $m_$ — масса фотона, $h$ — неизменная Планка. Масса $m_$ больше массы покоя, если у фотона масса отлична от нуля. Поэтому, если отыскать верхний предел для $m_$, получим ограничение для массы покоя фотона. Если существование электромагнитных волн с большой длиной волны (а лучше нескончаемой) обосновать, то можно утверждать, что $m_$ сильно мало. Более длинноватые электромагнитные волны, которые удалось следить на нынешний момент, образуются в виде стоячих волн в пространстве между поверхностью Земли и ионосферой. Они носят имя Шумана, а поточнее именуются резонансами Шумана. Малый резонанс Шумана соответствует частоте $\nu $=8Гц. С учетом расстояния от поверхности Земли было получено, что $m_
Для малых расстояний закон Кулона проверяется в опытах, связанных с простыми частичками. Уже опыты Резерфорда обосновали, что закон Кулона справедлив с большой точностью на расстоянии $^м$.
До работ Фарадея закон Кулона трактовался с позиций дальнодействия, другими словами числилось, что одно тело действует на другое без посредников (действие на расстоянии). В первой половине 18 века сложился другой взор на механизм взаимодействия, в согласовании с которым существует посредник, осуществляющий непрерывную передачу сил.(теория близкодействия). Сначала таким посредником назначили, так именуемый Мировой эфир. Состояние которого охарактеризовывали некоторыми механическими качествами. Попытка математического описания механической картины передачи электрических взаимодействий была изготовлена Максвеллом. Он пробовал представить электромагнитные силы в виде механических сил, которые вызываются натяжением и давлением в эфире. Позднее Максвелл перебежал к феноменологической формулировке взаимодействия и охарактеризовал состояние среды при помощи векторов: напряженности электростатического поля ($\overrightarrow$), электрического смещения ($\overrightarrow$), напряженности магнитного поля ($\overrightarrow$), магнитной индукции ($\overrightarrow$), которым не отдал никакой механической интерпретации. В 1864 г. Максвелл определил уравнения электромагнитного поля ( уравнения Максвелла). Надежда на механическое истолкование электромагнитных взаимодействий погибла. Поле стало основной сутью, средством которого осуществляется электромагнитное взаимодействие. Оно характеризуется величинами, которые не могут интерпретироваться в пределах механики. После того как Герц записал уравнения Максвелла в современном виде стало разумеется, что поле существует в пространстве и времени вместе с материей.
Готовые работы на аналогичную тему
Получить выполненную работу либо консультацию спеца по вашему учебному проекту Выяснить цена
Полевая трактовка закона Кулона
Пусть мы имеем два точечных заряда $q_1\ (точка\ 1)\ $ и $q_2$(точка 2).Тогда $<\overrightarrow>_$- сила, с которой заряд $q_1$ действует на заряд $q_2$. $<\overrightarrow>_$- сила, с которой заряд $q_2$ действует на заряд $q_1$. $<\overrightarrow>_$- вектор из точки (1) в точку (2), $<\overrightarrow>_$ — вектор из точки (2) в точку (1). Исходя из принятых нами обозначений, запишем закон Кулона:
По собственному физическому содержанию формулы (2) и (3) различны. Они определяют силы, которые действуют на 2-ой (2) и 1-ый (3) заряды, другими словами обрисовывают силы в различных точках места. Механизм же появления этих сил одинаков. Заряды вокруг себя делают электрическое поле. Это поле принято охарактеризовывать напряженностью ($\overrightarrow$). Напряженностью электрического поля является физическая величина, которая равна отношению силы, с которой действует поле на положительный заряд, помещенный в данную точку поля к заряду. Соответственно, с учетом (2,3), запишем:
Формула (4) обрисовывает напряженность электрического поля, которое появляется зарядом $q_1.$ Формула (5) охарактеризовывает силу, с которой поле с напряженностью $<\overrightarrow>_2$ действует на заряд, который находится в точке поля. Действие 1-го заряда на другой делится на:
- Точечный заряд делает вокруг себя электрическое поле, напряженность которого равна: \[\overrightarrow=\frac<4\pi <\varepsilon >_0>\frac\frac<\overrightarrow>\ \left(8\right),\]
где $\overrightarrow$- радиус — вектор, проведенный из точки нахождения заряда до точки, в какой определяется напряженность.
Эти два утверждения дают полевую трактовку Закона Кулона.
Если есть некоторое количество источников поля (количество зарядов $N$), то результирующую силу, действующую на пробный заряд $q$ можно отыскать как:
где $\overrightarrow>$ — сила, с которой N зарядов действуют на заряд $q$.
Закон Кулона в формуле (1) записан для вакуума, если мы имеем дело с некий средой, ее диэлектрические характеристики охарактеризовывает диэлектрическая проницаемость среды ($\varepsilon $), тогда уравнение (1) воспримет вид:
Задание: Три одинаковых точечных заряда величиной $q$ расположили в верхушках равностороннего треугольника. Найдите величину точечного заряда $Q$, который нужно поместить в центр тяжести треугольника, дабы система находилась в состоянии равновесия.
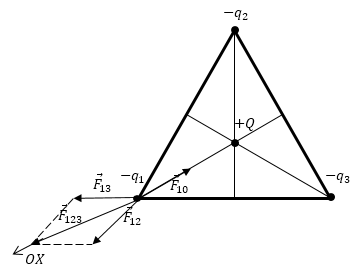
Для определенности допустим, что заряды в верхушках треугольника отрицательные, тогда на скрещении медиан (в центре тяжести) положительный.
Разглядим силы, которые действуют на заряд $_1$. Это будут три силы Кулона, две — отталкивания, со стороны зарядов в верхушках и одна — притяжения со стороны «центрального». Тогда условие равновесия сил запишем в виде:
Выберем ось OX, как обозначено на рис.1, найдем проекцию уравнения (1) на эту ось:
где $\alpha $- угол треугольника (так как треугольник равносторонний, поэтому, $\alpha =60<>^\circ $).
Так как по условию задачи треугольник равносторонний, заряды в верхушках однообразные и равны q, то $F_=F_$, а по закону Кулона:
где a — сторона треугольника. Для силы $F_$ по закону Кулона получим:
В таком случае выражение (1.2) запишем в виде:
где точка скрещения медиан разделяет их в соотношении 2:1, если считать от верхушки, поэтому:
Подставляем (1.6) в (1.5) выражаем $Q$, получаем:
Задание: Положительный точечный заряд 1 Кл находится на плоскости XOY в точке, которая определена радиус — вектором$\overrightarrow_1>=4\overrightarrow+6\overrightarrow$,(м) где $i$ и $j$ — орты осей. Найдите модуль напряженности электрического поля E в точке с радиус-вектором $\overrightarrow_2>=16\overrightarrow-\overrightarrow\ (м)$.
Найдем разность векторов $\overrightarrow_2>$-$\overrightarrow_1>$, получим:
\[\overrightarrow_2>-\overrightarrow_1>=12\overrightarrow-\overrightarrow\ \left(2.1\right).\]
Из закона Кулона выражение для напряженности электростатического поля может быть записано как:
Найдем $r$, получим:
\[r=\left|\overrightarrow_2>-\overrightarrow_1>\right|=\sqrt^2+7^2>\approx 13,89\ (м)\]