Также под законом Кулона понимается формула для вычисления электрического поля точечного заряда, вкупе с её обобщением на случайное рассредотачивание зарядов в пространстве:
Закон Кулона в традиционной электродинамике
Установление и формулировки закона
Закон открыт Шарлем Кулоном в 1785 году. Проведя огромное количество опытов с металлическими шариками, Кулон отдал такую формулировку закона:
Модуль силы взаимодействия 2-ух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и назад пропорционален квадрату расстояния между ними.
Сила взаимодействия 2-ух точечных зарядов в вакууме ориентирована вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и назад пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов различные, и силой отталкивания, если эти знаки одинаковы.
В векторном виде в формулировке Ш. Кулона закон записывается как
Условия применимости
Для того, дабы закон был верен, нужны:
- точечность зарядов, другими словами расстояние между заряженными телами должно быть много больше их размеров. Тут две обмолвки: а) существует обобщение закона Кулона на случай тел конечных размеров; б) можно обосновать, что сила взаимодействия 2-ух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными рассредотачиваниями равна силе взаимодействия 2-ух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии;
- их неподвижность. По другому вступают в силу дополнительные эффекты: магнитное поле перемещающегося заряда и соответственная ему дополнительная сила Лоренца, действующая на другой перемещающийся заряд;
- размещение зарядов в вакууме.
В отдельных ситуациях, с корректировками, закон может быть использован также для взаимодействий зарядов в среде и для перемещающихся зарядов [2] . Но в общем случае при наличии неоднородных диэлектриков он неприменим, так как кроме заряда q 1 > на зарад q 2 > действуют связанные заряды, возникшие при поляризации.
Выражения в различных системах единиц
В СГСЭ единица измерения заряда выбрана таким макаром, что коэффициент k равен единице.
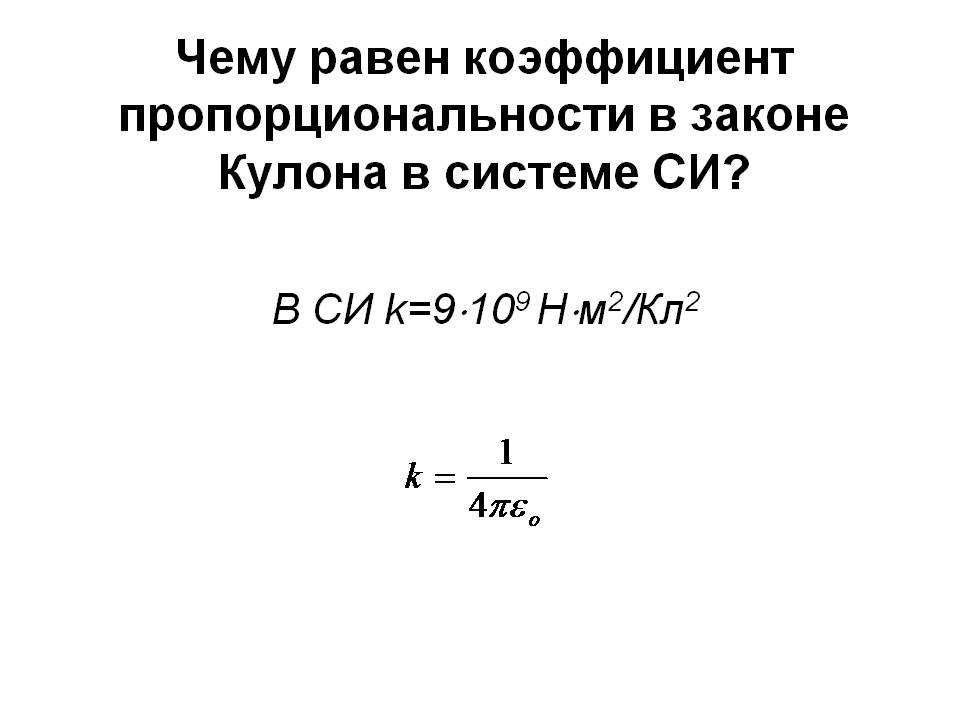
В Интернациональной системе единиц (СИ) одной из главных единиц является единица силы электрического тока — ампер, а единица заряда — кулон — производная от него. Величина ампера определена таким макаром, что k = c 2 ·10 −7 Гн/м = 8,9875517873681764⋅10 9 Н·м 2 /Кл 2 (либо Ф −1 ·м). В СИ коэффициент k записывается в виде:
В случае среды, заполненной нескончаемым однородным изотропным диэлектрическим веществом, в знаменатель формулы закона Кулона добавляется диэлектрическая проницаемость среды ε . Тогда
Закон Кулона и уравнения Максвелла
Закон Кулона и принцип суперпозиции для электрических полей в вакууме стопроцентно равносильны уравнениям Максвелла для электростатики d i v D → = ρ >=\rho > ( ρ — плотность заряда, D → <\displaystyle >> — вектор электрического смещения) и r o t E → = 0 >=0> ( E → <\displaystyle >> — напряжённость электрического поля). Другими словами закон Кулона и принцип суперпозиции для электрических полей производятся и тогда только тогда, когда производятся уравнения Максвелла для электростатики, и напротив, уравнения Максвелла для электростатики производятся, тогда когда производятся закон Кулона и принцип суперпозиции для электрических полей [3] .
Исторически закон Кулона был одним из эмпирических законов, служивших предпосылками для формулирования уравнения Максвелла. Но при современном изложении учения об электромагнетизме этот закон (равно как и, скажем, закон Ампера) часто позиционируется как следствие уравнений Максвелла, которым придаётся статус базовых аксиом.
Обобщение на случай рассредотачивания заряда
Закон Кулона и расчёт электрического поля
Взаимодействие 2-ух зарядов может быть истрактовано как взаимодействие 1-го из зарядов с электрическим полем, воздаваемым другим зарядом. Это становится виднее, если подходящим образом перегруппировать сомножители в выражении для силы:
Тем закон Кулона практически становится основой для вычисления поля. Так же, как и при рассмотрении силы, может быть обобщение последнего равенства на случай рассредотачивания зарядов.
Аналогии в других областях традиционной физики
Закон Кулона совсем аналогичен по форме закону глобального тяготения. При всем этом функцию гравитационных масс делают электрические заряды [4] различных символов.
Магнитостатическими аналогами закона Кулона являются закон Ампера (в части нахождения сил взаимодействия) и закон Био — Савара — Лапласа (в части расчёта по́ля).
Об открытии и исторической значимости закона
В первый раз изучить экспериментально закон взаимодействия электрически заряженных тел предложил [5] Г. В. Рихман в 1752—1753 гг. Он намеревался применять для этого сконструированный им электрометр-«указатель». Осуществлению этого плана помешала его трагическая смерть.
В 1759 г. доктор физики Санкт-Петербургской академии Ф. Эпинус, занявший кафедру Рихмана после его смерти, в первый раз представил [6] , что заряды должны вести взаимодействие назад пропорционально квадрату расстояния. В 1760 г. появилось короткое сообщение [7] о том, что Д. Бернулли в Базеле установил квадратичный закон при помощи сконструированного им электрометра. В 1767 г. Пристли в собственной «Истории электричества» [8] отметил, что опыт Франклина, обнаружившего отсутствие электрического поля снутри заряженного железного шара, может означать, что «сила электрического притяжения подчиняется этим же законам, что и сила тяжести, а поэтому, находится в зависимости от квадрата расстояния между зарядами» [9] . Шотландский физик Джон Робисон утверждал (1822), что в 1769 г. нашел, что шары с одинаковым электрическим зарядом отталкиваются с силой, назад пропорциональной квадрату расстояния между ними, и таким макаром предвосхитил открытие закона Кулона (1785) [10] .
Приблизительно за 11 лет до Кулона, в 1771 г., закон взаимодействия зарядов был экспериментально открыт Г. Кавендишем, но итог не был размещен и длительное время (выше 100 лет) оставался неведомым. Рукописи Кавендиша были вручены Дж. Максвеллу только в 1874 г одним из потомков Кавендиша на праздничном открытии Кавендишской лаборатории и размещены в 1879 г. [11] .
Сам Кулон занимался исследованием кручения нитей и изобрел крутильные весы. Он открыл свой закон, измеряя при помощи них силы взаимодействия заряженных шариков.
Закон Кулона является первым открытым количественным и сформулированным на математическом языке базовым законом для электромагнитных явлений. С открытия закона Кулона началась современная наука об электромагнетизме [12] .
Закон Кулона в квантовой механике
В квантовой механике закон Кулона формулируется не с помощью понятия силы, как в традиционной механике, а с помощью понятия возможной энергии кулоновского взаимодействия. В случае, когда рассматриваемая в квантовой механике система содержит электрически заряженные частички, к оператору Гамильтона системы добавляются слагаемые, выражающие потенциальную энергию кулоновского взаимодействия, так, как она рассчитывается в традиционной механике [13] . Это утверждение не следует из других аксиом квантовой механики, а получено путём обобщения опытнейших данных.
Так, оператор Гамильтона атома с зарядом ядра Z имеет вид:
Закон Кулона исходя из убеждений квантовой электродинамики
Согласно квантовой электродинамике, электромагнитное взаимодействие заряженных частиц осуществляется путём обмена виртуальными фотонами между частичками. Принцип неопределённости для времени и энергии допускает существование виртуальных фотонов на время между моментами их испускания и поглощения. Чем меньше расстояние между заряженными частичками, тем наименьшее время необходимо виртуальным фотонам для преодоления этого расстояния и поэтому, тем большая энергия виртуальных фотонов допускается принципом неопределенности. При малых расстояниях между зарядами принцип неопределённости допускает обмен как длинноволновыми, так и коротковолновыми фотонами, а при огромных расстояниях в обмене участвуют только длинноволновые фотоны. Таким макаром, при помощи квантовой электродинамики можно вывести закон Кулона [15] [16] .
Степень точности закона Кулона
Закон Кулона — экспериментально установленный факт. Его справедливость не один раз подтверждалась всё более точными тестами. Одним из направлений таких тестов является проверка того, отличается ли показатель степени r в законе от 2. Для поиска этого отличия применяется тот факт, что если степень точно равна двум, то поле снутри полости в проводнике отсутствует, какова бы ни была форма полости либо проводника [17] .
Такие опыты в первый раз провел Кавендиш и повторил Максвелл в улучшенном виде, получив для наибольшего отличия показателя в степени от 2-ух величину 1 21600 >> [18] .
Опыты, проведённые в 1971 г. в США Э. Р. Уильямсом, Д. Е. Фоллером и Г. А. Хиллом, проявили, что показатель степени в законе Кулона равен 2 с точностью до ( 3 , 1 ± 2 , 7 ) × 10 − 16 > [19] .
Для проверки точности закона Кулона на внутриатомных расстояниях У. Ю. Лэмбом и Р. Резерфордом в 1947 г. были применены измерения относительного расположения уровней энергии водорода. Было установлено, что и на расстояниях порядка атомных 10 −8 см, показатель степени в законе Кулона отличается от 2 менее чем на 10 −9 [20] [21] .
Поправки к закону в квантовой электродинамике
где m e > — масса электрона, ℏ — неизменная Планка, c — скорость света) становятся существенными нелинейные эффекты квантовой электродинамики: на обмен виртуальными фотонами накладывается генерация виртуальных электрон-позитронных (также мюон-антимюонных и таон-антитаонных) пар, также миниатюризируется воздействие экранирования (см. перенормировка). Оба эффекта ведут к возникновению экспоненциально убывающих членов порядка e − 2 r / λ e >> в выражении для возможной энергии взаимодействия зарядов и, как итог, к повышению силы взаимодействия по сопоставлению с вычисляемой по закону Кулона.
К примеру, выражение для потенциала точечного заряда Q в системе СГС, с учётом радиационных поправок первого порядка, воспринимает вид [23] :
В сильных наружных электромагнитных полях, составляющих приметную долю от поля пробоя вакуума (порядка m e c 2 e λ e ∼ c^>>>\sim > 10 18 В/м либо m e c e λ e ∼ c>>>\sim > 10 9 Тл, такие поля наблюдаются, к примеру, поблизости некоторых типов нейтронных звёзд, а конкретно магнитаров) закон Кулона также нарушается в силу дельбрюковского рассеяния обменных фотонов на фотонах наружного поля и других, более сложных нелинейных эффектов. Это явление уменьшает кулоновскую силу не только лишь в микро-, но и в макромасштабах, а именно, в сильном магнитном поле кулоновский потенциал падает не назад пропорционально расстоянию, а экспоненциально [24] .
Закон Кулона и поляризация вакуума
Эффект Юлинга
Явление отличия электростатического потенциала точечных зарядов в вакууме от значения закона Кулона понятно как эффект Юлинга, который в первый раз вычислил отличия от закона Кулона для атома водорода. Эффект Юлинга даёт поправку к лэмбовскому сдвигу 27 МГц [28] [29] .
Закон Кулона
Также под законом Кулона понимается формула для вычисления электрического поля точечного заряда, вкупе с её обобщением на случайное рассредотачивание зарядов в пространстве:
Содержание
Закон Кулона в традиционной электродинамике
Установление и формулировки закона
Закон открыт Шарлем Кулоном в 1785 году. Проведя огромное количество опытов с металлическими шариками, Кулон отдал такую формулировку закона:
Модуль силы взаимодействия 2-ух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и назад пропорционален квадрату расстояния между ними.
Сила взаимодействия 2-ух точечных зарядов в вакууме ориентирована вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и назад пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов различные, и силой отталкивания, если эти знаки одинаковы.
В векторном виде в формулировке Ш. Кулона закон записывается как
Условия применимости
Для того, дабы закон был верен, нужны:
- точечность зарядов, другими словами расстояние между заряженными телами должно быть много больше их размеров. Тут две обмолвки: а) существует обобщение закона Кулона на случай тел конечных размеров; б) можно обосновать, что сила взаимодействия 2-ух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными рассредотачиваниями равна силе взаимодействия 2-ух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии;
- их неподвижность. По другому вступают в силу дополнительные эффекты: магнитное поле перемещающегося заряда и соответственная ему дополнительная сила Лоренца, действующая на другой перемещающийся заряд;
- размещение зарядов в вакууме.
В отдельных ситуациях, с корректировками, закон может быть использован также для взаимодействий зарядов в среде и для перемещающихся зарядов [2] . Но в общем случае при наличии неоднородных диэлектриков он неприменим, так как кроме заряда q 1 > на зарад q 2 > действуют связанные заряды, возникшие при поляризации.
Выражения в различных системах единиц
В СГСЭ единица измерения заряда выбрана таким макаром, что коэффициент k равен единице.
Закон Кулона и уравнения Максвелла
Закон Кулона и принцип суперпозиции для электрических полей в вакууме стопроцентно равносильны уравнениям Максвелла для электростатики d i v D → = ρ >=\rho > ( ρ — плотность заряда, D → <\displaystyle >> — вектор электрического смещения) и r o t E → = 0 >=0> ( E → <\displaystyle >> — напряжённость электрического поля). Другими словами закон Кулона и принцип суперпозиции для электрических полей производятся и тогда только тогда, когда производятся уравнения Максвелла для электростатики, и напротив, уравнения Максвелла для электростатики производятся, тогда когда производятся закон Кулона и принцип суперпозиции для электрических полей [3] .
Исторически закон Кулона был одним из эмпирических законов, служивших предпосылками для формулирования уравнения Максвелла. Но при современном изложении учения об электромагнетизме этот закон (равно как и, скажем, закон Ампера) часто позиционируется как следствие уравнений Максвелла, которым придаётся статус базовых аксиом.
Обобщение на случай рассредотачивания заряда
Закон Кулона и расчёт электрического поля
Взаимодействие 2-ух зарядов может быть истрактовано как взаимодействие 1-го из зарядов с электрическим полем, воздаваемым другим зарядом. Это становится виднее, если подходящим образом перегруппировать сомножители в выражении для силы:
Тем закон Кулона практически становится основой для вычисления поля. Так же, как и при рассмотрении силы, может быть обобщение последнего равенства на случай рассредотачивания зарядов.
Аналогии в других областях традиционной физики
Закон Кулона совсем аналогичен по форме закону глобального тяготения. При всем этом функцию гравитационных масс делают электрические заряды [4] различных символов.
Магнитостатическими аналогами закона Кулона являются закон Ампера (в части нахождения сил взаимодействия) и закон Био — Савара — Лапласа (в части расчёта по́ля).
Об открытии и исторической значимости закона
В первый раз изучить экспериментально закон взаимодействия электрически заряженных тел предложил [5] Г. В. Рихман в 1752—1753 гг. Он намеревался применять для этого сконструированный им электрометр-«указатель». Осуществлению этого плана помешала его трагическая смерть.
В 1759 г. доктор физики Санкт-Петербургской академии Ф. Эпинус, занявший кафедру Рихмана после его смерти, в первый раз представил [6] , что заряды должны вести взаимодействие назад пропорционально квадрату расстояния. В 1760 г. появилось короткое сообщение [7] о том, что Д. Бернулли в Базеле установил квадратичный закон при помощи сконструированного им электрометра. В 1767 г. Пристли в собственной «Истории электричества» [8] отметил, что опыт Франклина, обнаружившего отсутствие электрического поля снутри заряженного железного шара, может означать, что «сила электрического притяжения подчиняется этим же законам, что и сила тяжести, а поэтому, находится в зависимости от квадрата расстояния между зарядами» [9] . Шотландский физик Джон Робисон утверждал (1822), что в 1769 г. нашел, что шары с одинаковым электрическим зарядом отталкиваются с силой, назад пропорциональной квадрату расстояния между ними, и таким макаром предвосхитил открытие закона Кулона (1785) [10] .
Приблизительно за 11 лет до Кулона, в 1771 г., закон взаимодействия зарядов был экспериментально открыт Г. Кавендишем, но итог не был размещен и длительное время (выше 100 лет) оставался неведомым. Рукописи Кавендиша были вручены Дж. Максвеллу только в 1874 г одним из потомков Кавендиша на праздничном открытии Кавендишской лаборатории и размещены в 1879 г. [11] .
Сам Кулон занимался исследованием кручения нитей и изобрел крутильные весы. Он открыл свой закон, измеряя при помощи них силы взаимодействия заряженных шариков.
Закон Кулона является первым открытым количественным и сформулированным на математическом языке базовым законом для электромагнитных явлений. С открытия закона Кулона началась современная наука об электромагнетизме [12] .
Закон Кулона в квантовой механике
В квантовой механике закон Кулона формулируется не с помощью понятия силы, как в традиционной механике, а с помощью понятия возможной энергии кулоновского взаимодействия. В случае, когда рассматриваемая в квантовой механике система содержит электрически заряженные частички, к оператору Гамильтона системы добавляются слагаемые, выражающие потенциальную энергию кулоновского взаимодействия, так, как она рассчитывается в традиционной механике [13] . Это утверждение не следует из других аксиом квантовой механики, а получено путём обобщения опытнейших данных.
Закон Кулона исходя из убеждений квантовой электродинамики
Согласно квантовой электродинамике, электромагнитное взаимодействие заряженных частиц осуществляется путём обмена виртуальными фотонами между частичками. Принцип неопределённости для времени и энергии допускает существование виртуальных фотонов на время между моментами их испускания и поглощения. Чем меньше расстояние между заряженными частичками, тем наименьшее время необходимо виртуальным фотонам для преодоления этого расстояния и поэтому, тем большая энергия виртуальных фотонов допускается принципом неопределенности. При малых расстояниях между зарядами принцип неопределённости допускает обмен как длинноволновыми, так и коротковолновыми фотонами, а при огромных расстояниях в обмене участвуют только длинноволновые фотоны. Таким макаром, при помощи квантовой электродинамики можно вывести закон Кулона [15] [16] .
Степень точности закона Кулона
Такие опыты в первый раз провел Кавендиш и повторил Максвелл в улучшенном виде, получив для наибольшего отличия показателя в степени от 2-ух величину 1 21600 >> [18] .
Опыты, проведённые в 1971 г. в США Э. Р. Уильямсом, Д. Е. Фоллером и Г. А. Хиллом, проявили, что показатель степени в законе Кулона равен 2 с точностью до ( 3 , 1 ± 2 , 7 ) × 10 − 16 > [19] .
Для проверки точности закона Кулона на внутриатомных расстояниях У. Ю. Лэмбом и Р. Резерфордом в 1947 г. были применены измерения относительного расположения уровней энергии водорода. Было установлено, что и на расстояниях порядка атомных 10 −8 см, показатель степени в законе Кулона отличается от 2 менее чем на 10 −9 [20] [21] .
Поправки к закону в квантовой электродинамике
где m e >  — масса электрона, ℏ  — неизменная Планка, c  — скорость света) становятся существенными нелинейные эффекты квантовой электродинамики: на обмен виртуальными фотонами накладывается генерация виртуальных электрон-позитронных (также мюон-антимюонных и таон-антитаонных) пар, также миниатюризируется воздействие экранирования (см. перенормировка). Оба эффекта ведут к возникновению экспоненциально убывающих членов порядка e − 2 r / λ e >> в выражении для возможной энергии взаимодействия зарядов и, как итог, к повышению силы взаимодействия по сопоставлению с вычисляемой по закону Кулона.
К примеру, выражение для потенциала точечного заряда Q в системе СГС, с учётом радиационных поправок первого порядка, воспринимает вид [23] :
В сильных наружных электромагнитных полях, составляющих приметную долю от поля пробоя вакуума (порядка m e c 2 e λ e ∼ c^>>>\sim > 10 18 В/м либо m e c e λ e ∼ c>>>\sim > 10 9 Тл, такие поля наблюдаются, к примеру, поблизости некоторых типов нейтронных звёзд, а конкретно магнитаров) закон Кулона также нарушается в силу дельбрюковского рассеяния обменных фотонов на фотонах наружного поля и других, более сложных нелинейных эффектов. Это явление уменьшает кулоновскую силу не только лишь в микро-, но и в макромасштабах, а именно, в сильном магнитном поле кулоновский потенциал падает не назад пропорционально расстоянию, а экспоненциально [24] .
Закон Кулона и поляризация вакуума
Эффект Юлинга
Явление отличия электростатического потенциала точечных зарядов в вакууме от значения закона Кулона понятно как эффект Юлинга, который в первый раз вычислил отличия от закона Кулона для атома водорода. Эффект Юлинга даёт поправку к лэмбовскому сдвигу 27 МГц [28] [29] .