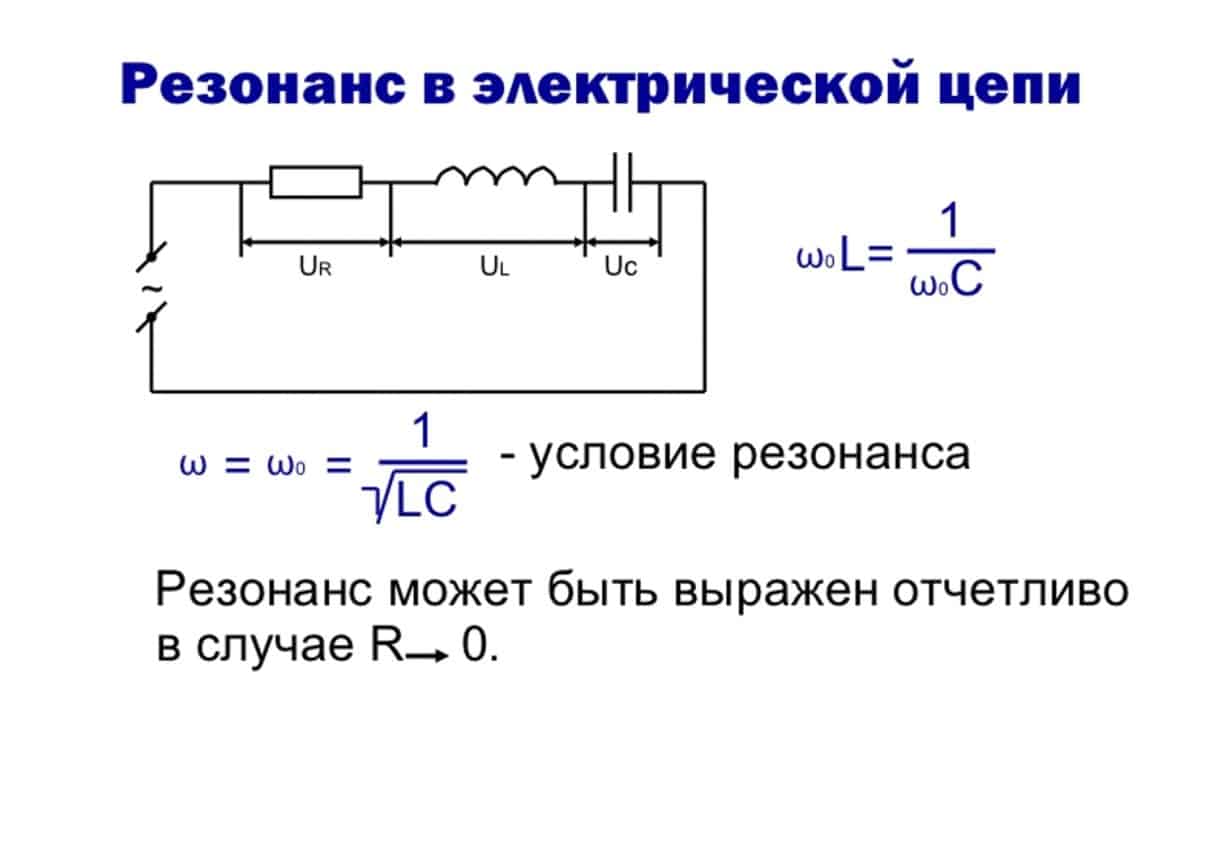
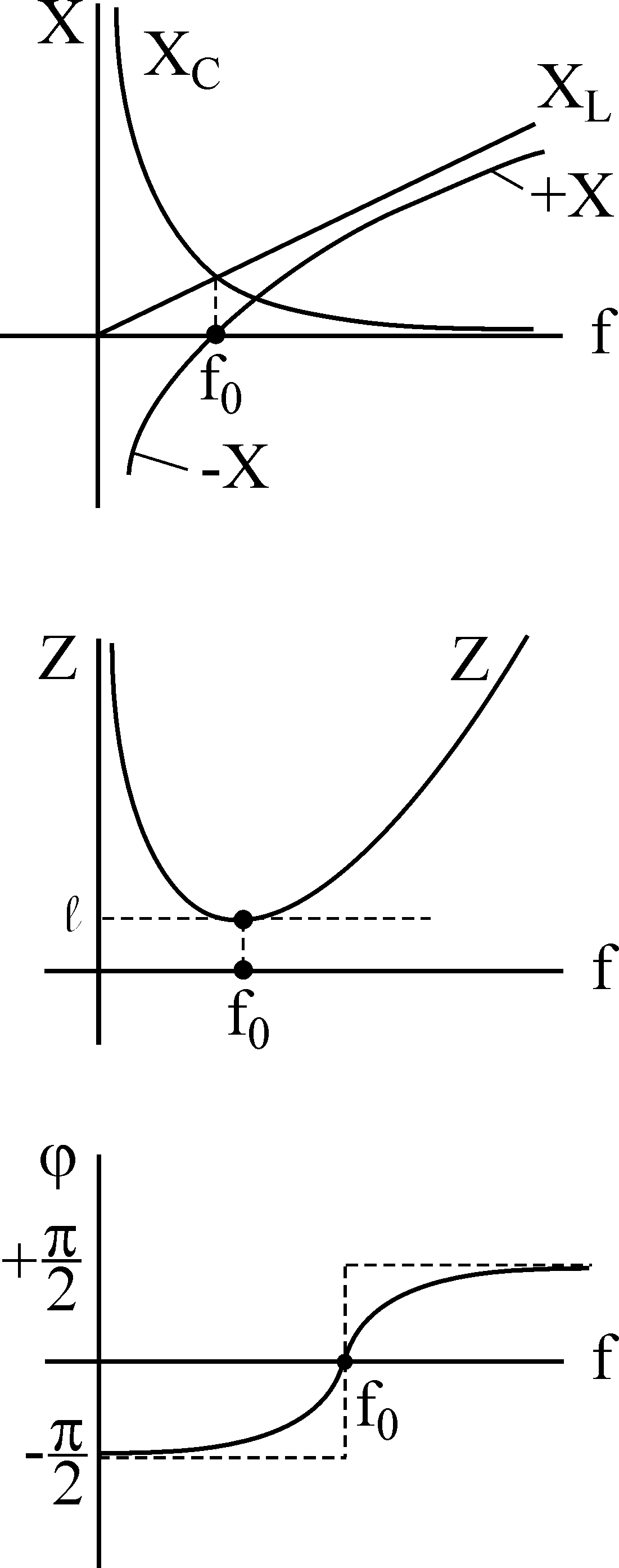Под резонансом в электрической цепи понимают такое ее состояние, когда ток и напряжение совпадают по фазе и вся цепь ведет себя как чисто активная (рис. 1.18).
Рис. 1.18. Резонансная цепь (а) и векторная диаграмма при резонансе (б)
(из определения резонанса);
(условие резонанса напряжений);
Если то , т.е. напряжение на реактивных элементах цепи может быть больше напряжения, подводимого ко всей цепи.
,
,
т.е. цепь из сети реактивную мощность не потребляет и в сеть её не дает;
;
В момент резонанса происходит обмен энергии между L и C. Из сети реактивная мощность не потребляется и в сеть не отдается, поэтому, цепь ведет себя как чисто активная.
35. Резонанс токов появляется в цепях переменного тока состоящих из источника колебаний и параллельного колебательного контура. Резонанс тока это повышение тока проходящего через элементы контура при всем этом повышение потребление тока от источника не происходит.
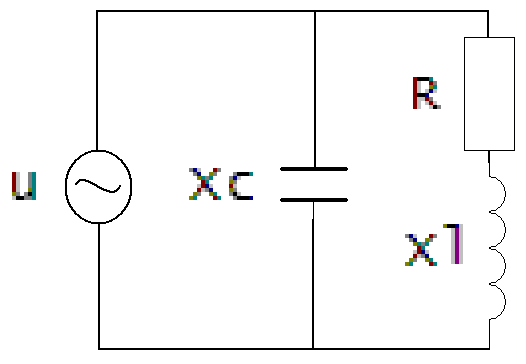
Набросок 1 — параллельный колебательный контур
Для появления резонанса токов нужно дабы реактивные сопротивления емкости и индуктивности контура были равны. Также частота собственных колебаний контура была равна частоте колебаний источника тока.
Во время пришествия резонанса токов либо так именуемого параллельного резонанса напряжение на элементах контура остается постоянным и равным напряжению, которое делает источник. Так как он подключен параллельно контуру. Потребление тока от источника будет мало, так как сопротивление контура при пришествии резонанса резко возрастет.
Набросок 2 — зависимость полного сопротивления контура и тока от частоты
Сопротивление колебательного контура относительно источника колебаний будет иметь чисто активный нрав. Другими словами не будет, провялятся ни емкостная, ни индуктивная составляющая. И сдвиг фаз между током и напряжением будет отсутствовать.
В тоже время ток через индуктивность будет отставать от напряжения на 90 градусов. А ток в емкости буде опережать напряжение на те же 90 градусов. Таким макаром, токи в реактивных элементах контура будут смещены по фазе на 180 градусов друг относительно друга.
В конечном итоге выходит, что в параллельном колебательном контуре протекают реактивные токи довольно большой величины, но при всем этом он от источника напряжения потребляет малый ток нужный только для компенсации утрат в контуре. Эти утраты обоснованы наличием активного сопротивления сосредоточенного по большей части в индуктивности.
Источник затрачивает энергию при включении, заряжая емкость. Дальше энергия, скопленная в электрическом поле конденсатора, перебегает в энергию магнитного поля индуктивности. Индуктивность возвращает энергию емкости, и процесс повторяется опять. Источник напряжения только должен восполнить энергопотери в активном сопротивлении контура.
1. Способ контурных токов применяется обыденным методом, но, к напряжениям самоиндукции на катушках добавляем напряжения обоюдной индукции (типа ). Контурные токи лучше выбирать так, дабы на каждую катушку приходился свой контурный ток.
Примечание: Перед М берем "-", так как имеем встречное включение
| б. Пример |
Примечание: Перед М берем "+", так как имеем согласное включение
2. Развязка индуктивных связей применяется для замены индуктивно связанных катушек с одним общим зажимом на три обыденных индуктивности.
Примечание: При другом расположении одноименных зажимов следует поменять везде символ перед М.
3. Внедрение заместо реальных трансформаторов эквивалентных схем с безупречными трансформаторами нередко упрощает расчет.
28 В электротехнике и электронике обширно применяются устройства, которые содержат индуктивные катушки, связанные общими магнитными потоками. Примером такового устройства является трансформатор, который служит для преобразования уровней переменных напряжений и токов и для согласования сопротивлений отдельных участков цепи.
Физическая картина заключалась в следующем: переменный ток , протекая по виткам катушки (рис. 8.1, а) делает переменный магнитный поток , который сцепляясь с витками катушки, обуславливает возникновение ЭДС самоиндукции eL, противодействующей по закону Ленца изменению потокосцепления , другими словами
где — индуктивность, численно равная отношению потокосцепления самоиндукции к току, его обуславливающему.
Сейчас разглядим явление взаимоиндукции, другими словами явление наведения ЭДС в одной электрической цепи при изменении в ней потокосцепления, вызванного конфигурацией тока в другой электрической цепи. Для этого проанализируем картину магнитного поля индуктивно-связанных катушек (рис. 8.1,б).
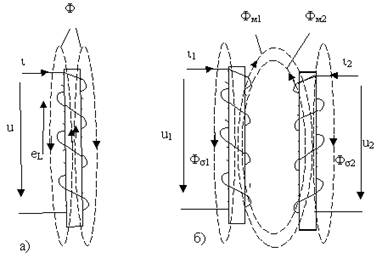
Рис.8.1 — К определению индуктивно связанных цепей
Связь магнитных потоков катушек обусловливает их индуктивную связь. Взаимно индуктивная связь проявляется в наведении ЭДС (именуемой ЭДС взаимоиндукции) в одной катушке при изменении тока в другой близко расположенной катушке.
Цепи, в каких наводятся ЭДС взаимоиндукции, именуют индуктивно связанными цепями.
Разглядим цепь, состоящую из 2-ух индуктивных катушек, намотан-ных на общий сердечник (набросок 8.2). На схеме обозначено: L1, R1 и L2, R2 – индуктивности и активные сопротивления первой и 2-ой катушек; М – обоюдная индуктивность.
Набросок 8.2 ‑ Схема замещения 2-ух, индуктивно связанных,
Обоюдная индуктивность M находится в зависимости от индуктивностей обоих контуров и их обоюдного расположения, потому при некоторой ориентации даже близко расположенных контуров обоюдная индуктивность может быть равной нулю. Единица измерения обоюдной индуктивности и индуктивности одинакова − генри.
Любая из катушек пронизывается 2-мя магнитными потоками: потоком самоиндукции, вызванным своим током, и потоком взаимоиндукции, вызванным током другой катушки.
В согласовании с принципом наложения потокосцепление первой катушки
Потокосцепление 2-ой катушки
Значения обоюдной индуктивности М в выражениях (8.1) и (8.2) одинаковы и не могут превосходить среднего геометрического из значений и :L1 и L2:
где k – коэффициент связи, характеризующий магнитную связь между катушками. Его величина равна отношению обоюдной индуктивности и среднего геометрического значения индуктивностей обеих катушек:
где XL1 и XL2 – индуктивные сопротивления катушек.
В пределе, когда магнитный поток одной катушки на сто процентов пронизывает витки другой, k=1. При отсутствии магнитной связи k=0.
Знаки слагаемых в (8.1) и (8.2) зависят от обоюдного направления магнитных потоков катушек. В свою очередь, направления магнитных потоков зависят как от направления токов в катушках, так и от их обоюдного расположения.
Если катушки включены таким макаром, что потоки складываются, то такое включение именуют согласным. Если магнитные потоки ориентированы навстречу друг дружке, то катушки включены встречно.
При согласном направлении токов в 2-ух индуктивно связанных ка-тушках зажимы этих катушек, относительно которых токи ориентированы идиентично, именуютодноименными. Одноименные зажимы принято обозначать точками либо звездочками.
На физическом уровне направления магнитных потоков в катушках определяется правилом правоходового винта. К примеру, потоки Фм1 и Фм2 на рис. 8.3,а ориентированы обратно при данных направлениях токов i 1 и i 2 , т.е. катушки включены встречно. Но, если б эти токи были нацелены идиентично относительно зажимов соответственно 1 и 4, то потоки могли быть ориентированы идиентично. Поэтому, эти зажимы можно считать одноименными.
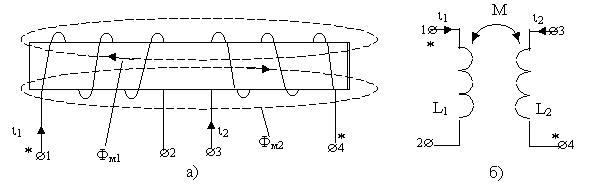
Набросок 8.3 — Встречное включение катушек
На рис. 8.3,б изображена эл. схема, соответственная рисунку 8.3,а, где
наличие индуктивной связи между катушками показано дугой с стрелками, над которой стоит знак "М", а одноименные зажимы помечены знаками (*).
Определим напряжения на зажимах индуктивно связанных катушек на базе второго закона Кирхгофа:
Основной формой расчета цепей синусоидального тока является способ всеохватывающих амплитуд. Разглядим использование этого способа для расчета индуктивно связанных цепей. Пусть цепь на рисунке 8.1 находится в режиме гармонических колебаний. Запишем уравнения (8.3), (8.4) в всеохватывающей форме:
где — комплекс сопротивления взаимоиндукции; символ плюс (+М) ставят при согласном включении катушек; символ минус (-М) — при их встречном включении.
20. (. )Резонанс напряжений. Условия резонанса. Добротность контура. Главные частотные свойства.
Резонанс напряжений – явление, при котором цепь содержащая активные и реактивные сопротивления, будет только активное сопротивление (XL — XC = 0). При всем этом ток в цепи совпадает по фазе с напряжением. Условие появление резонанса напряжений – равенство нулю реактивного сопротивления.
Обычно наблюдается в цепях, содержащих катушку и конденсатор, включенные последовательно.
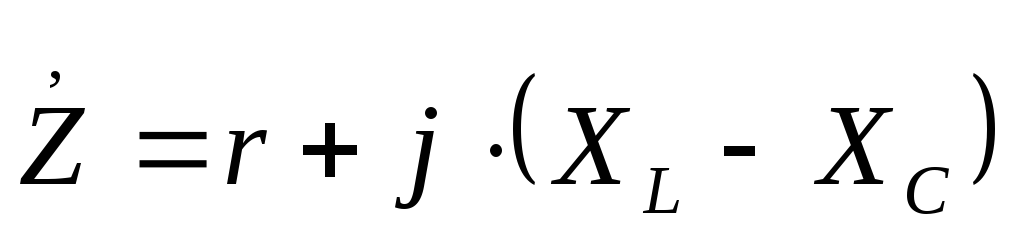
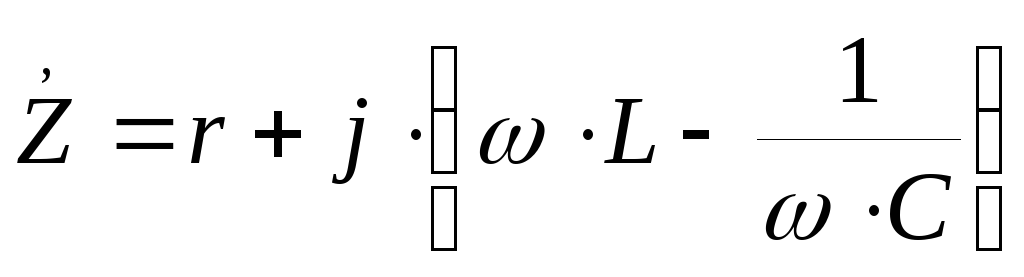
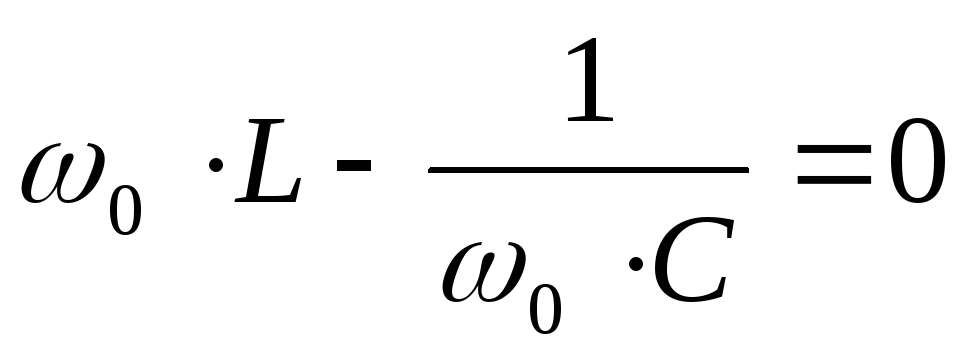
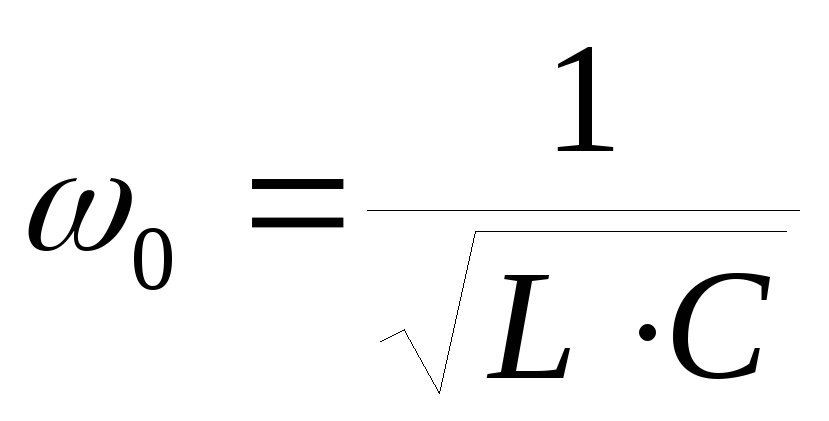
–резонансная частота
При резонансе напряжений ток максимален, так как сопротивление мало, а
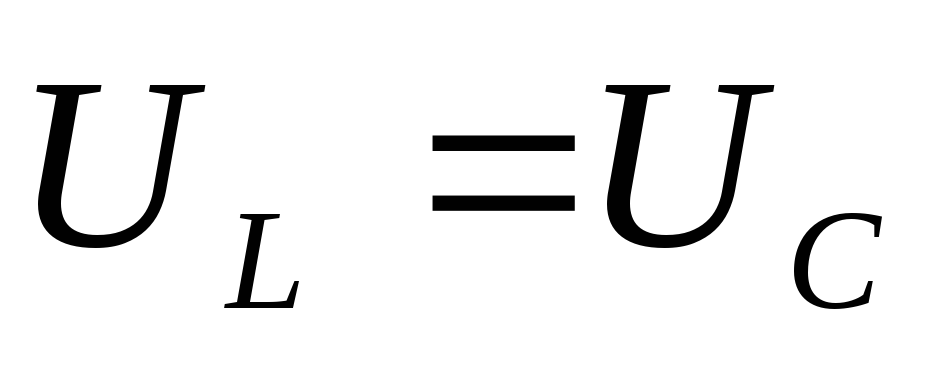
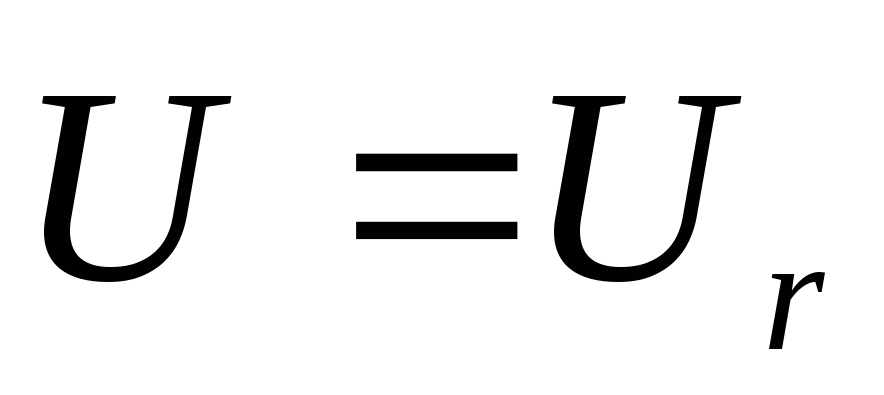
и таким макаром
Нередко для оценки цепи в режиме резонанса используют такие свойства как характеристическое сопротивление и добротность контура.
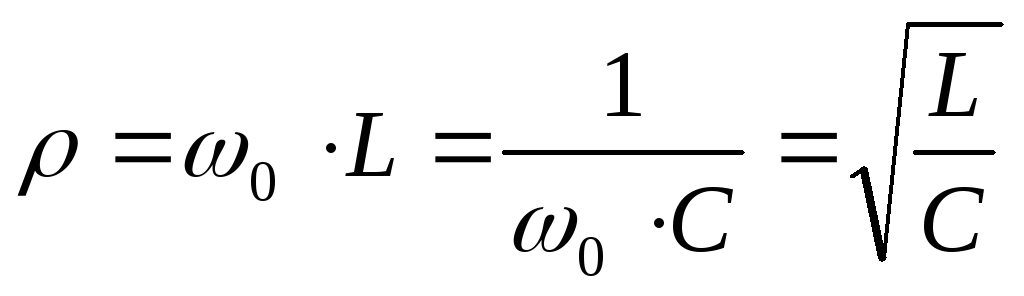
— характеристическое сопротивление контура. В простом случае это сопротивление на одном из реактивных частей.
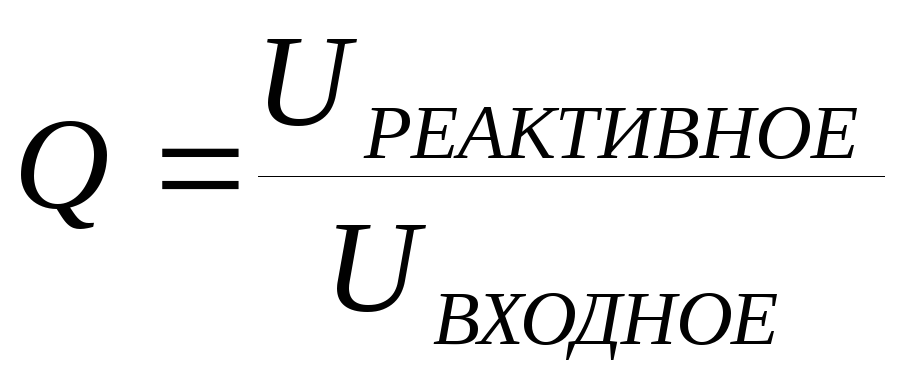
Добротностью контура именуется отношение модуля реактивной составляющей напряжения в цепи к модулю входного напряжения в момент резонанса.
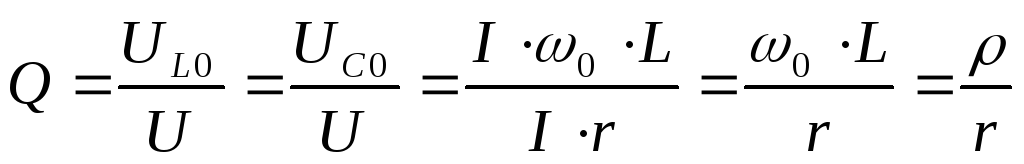
Зависимость от частоты характеристик цепи именуют частотными чертами
21. Резонанс напряжений. Главные частотные свойства. Векторные диаграммы.
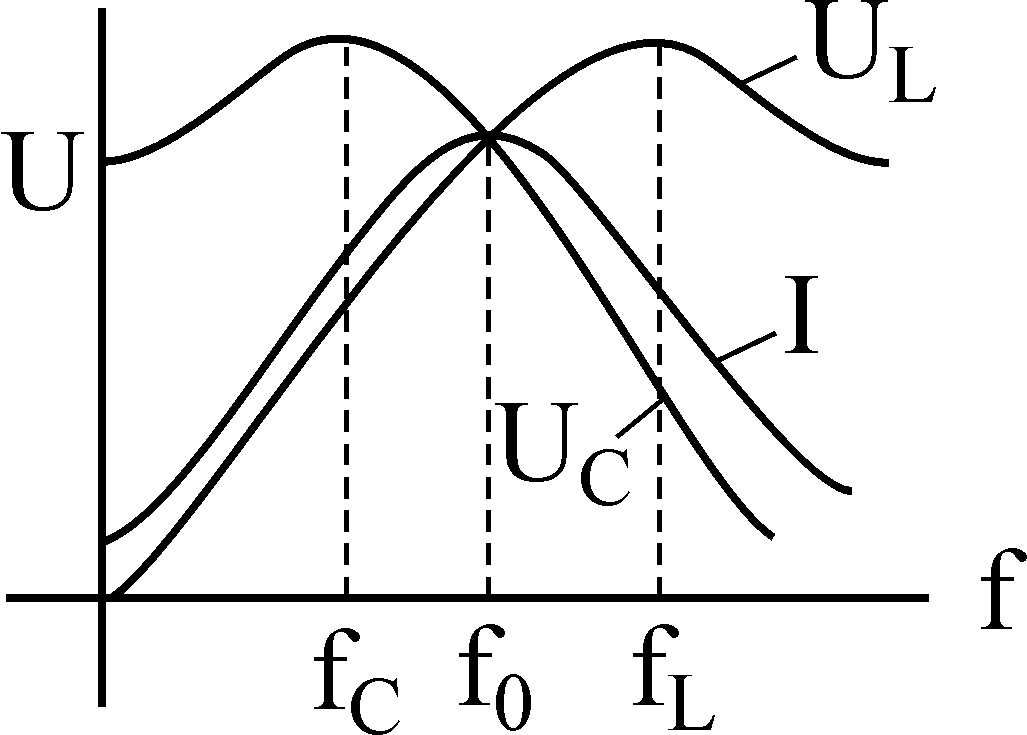
Частотными чертами именуются зависимости от частоты характеристик, характеризующих характеристики цепи. Зависимости тока и напряжения в цепи от частоты принято именовать резонансными кривыми.
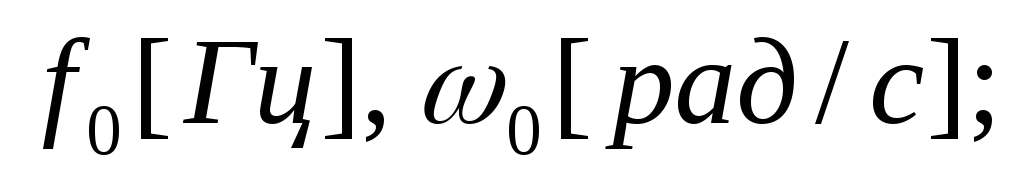
резонансная частота —
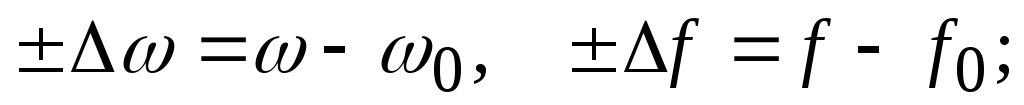
абсолютная настройка по частоте —
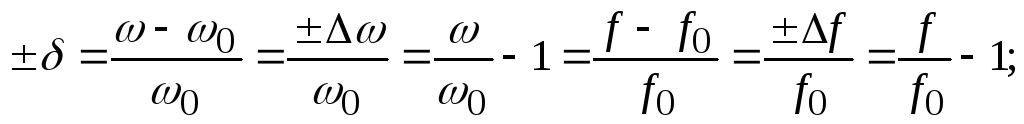
относительная настройка —
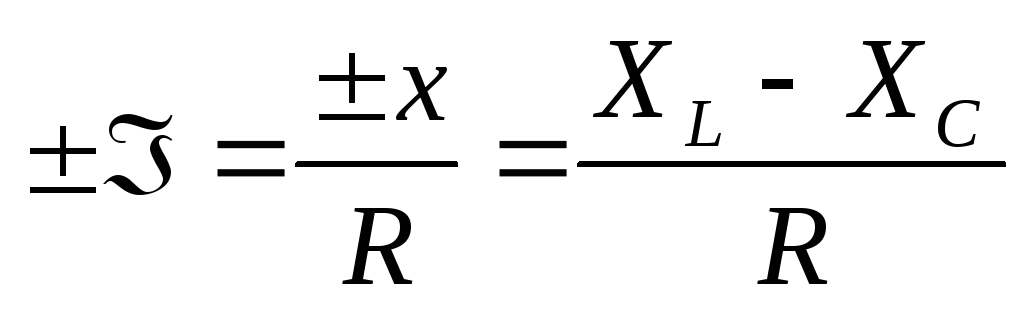
обобщенная настройка (кси) –
(при всем этом все опции положительны, при ff0, отрицательны при f f0, при очень малых настройках (),).
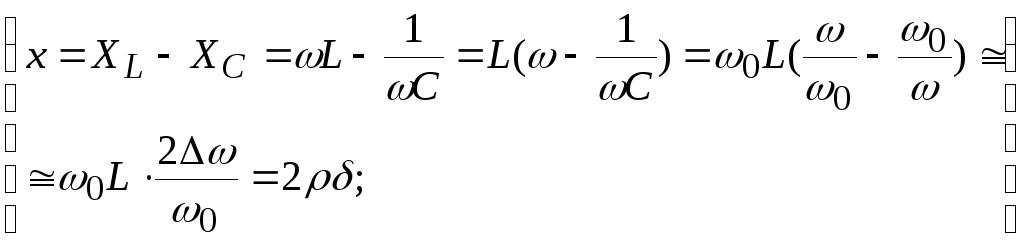
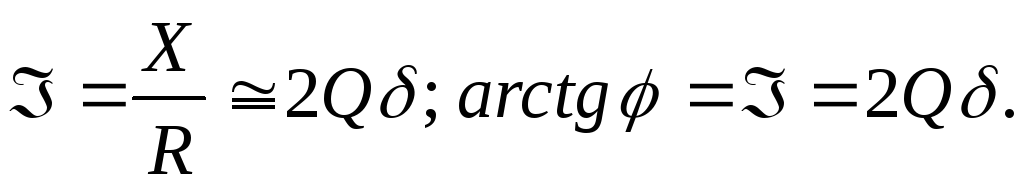
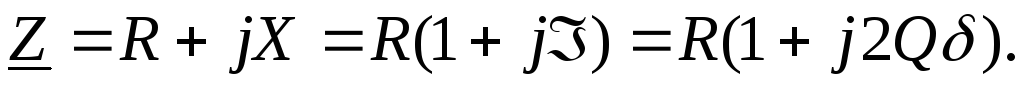
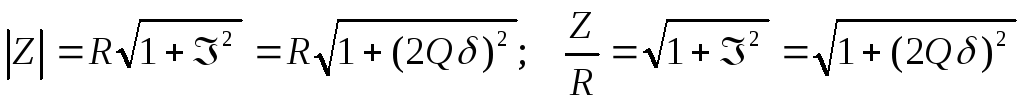
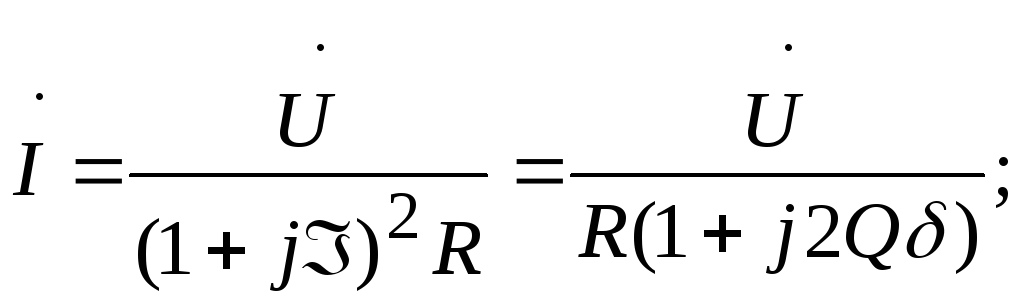
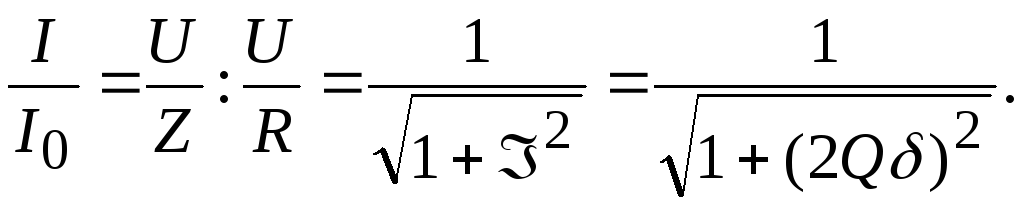
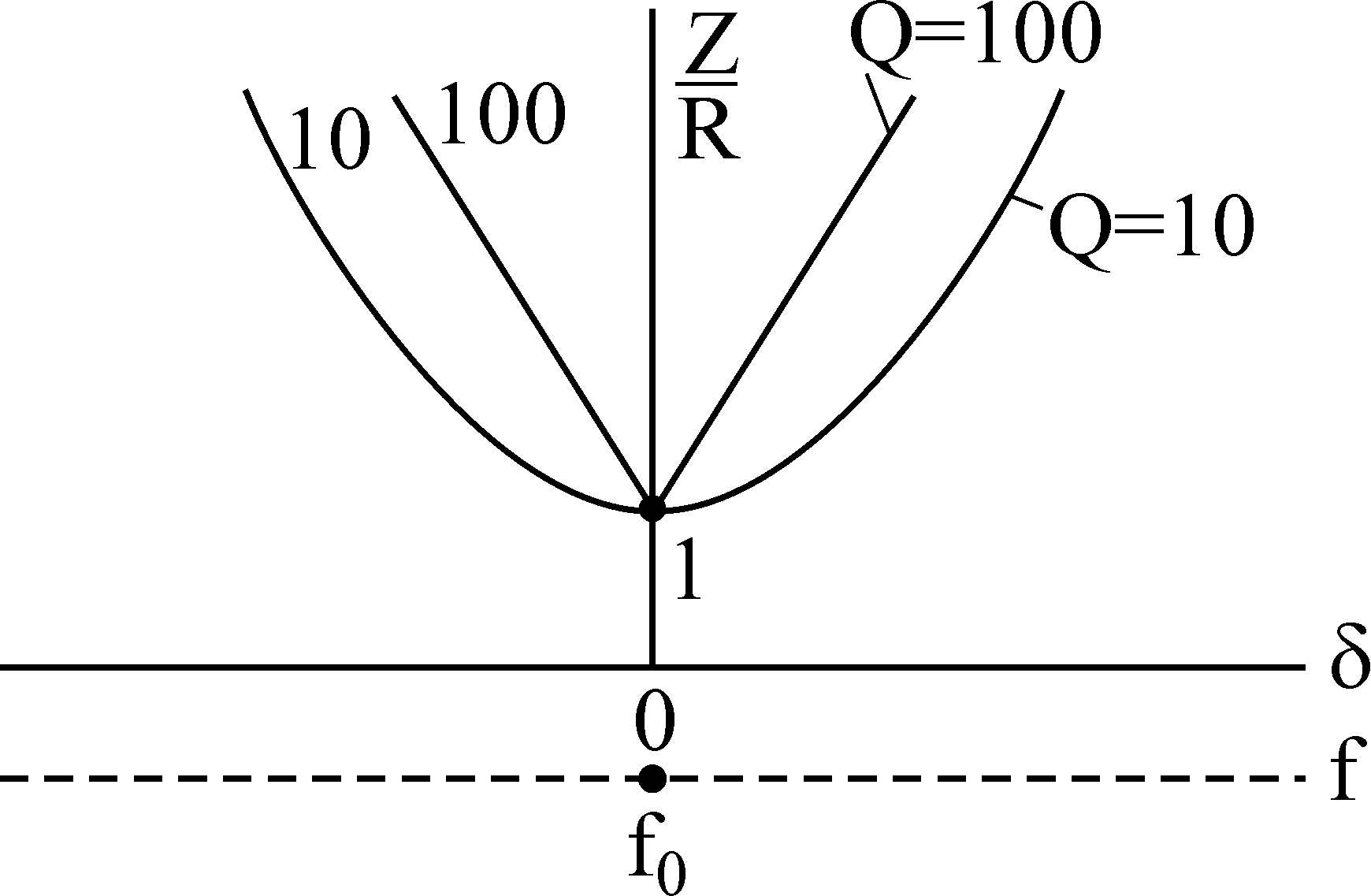
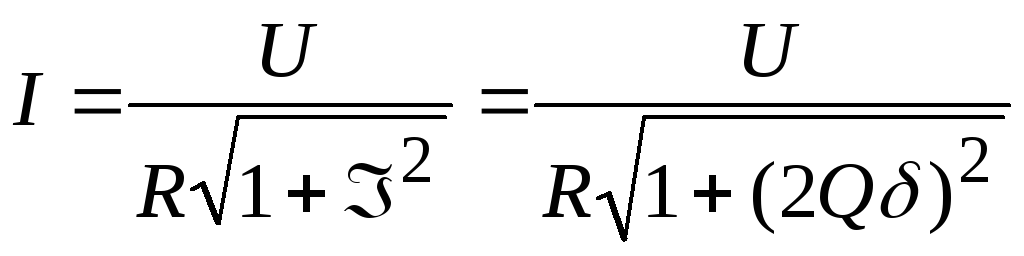
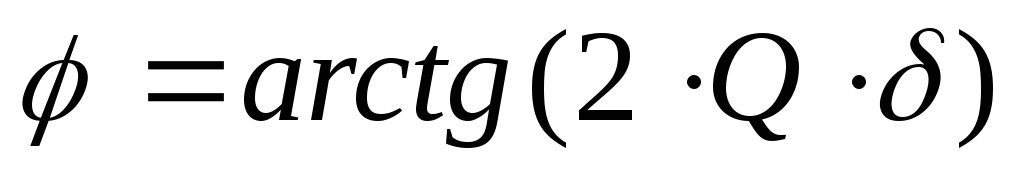
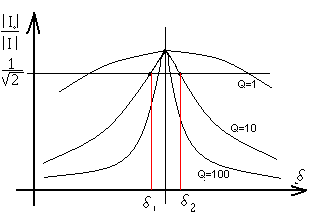
Сейчас можно выстроить свойства I, Z, зависимо от .

При всем этом можно созидать, что зависимости от относительной опции различаются по величине добротности
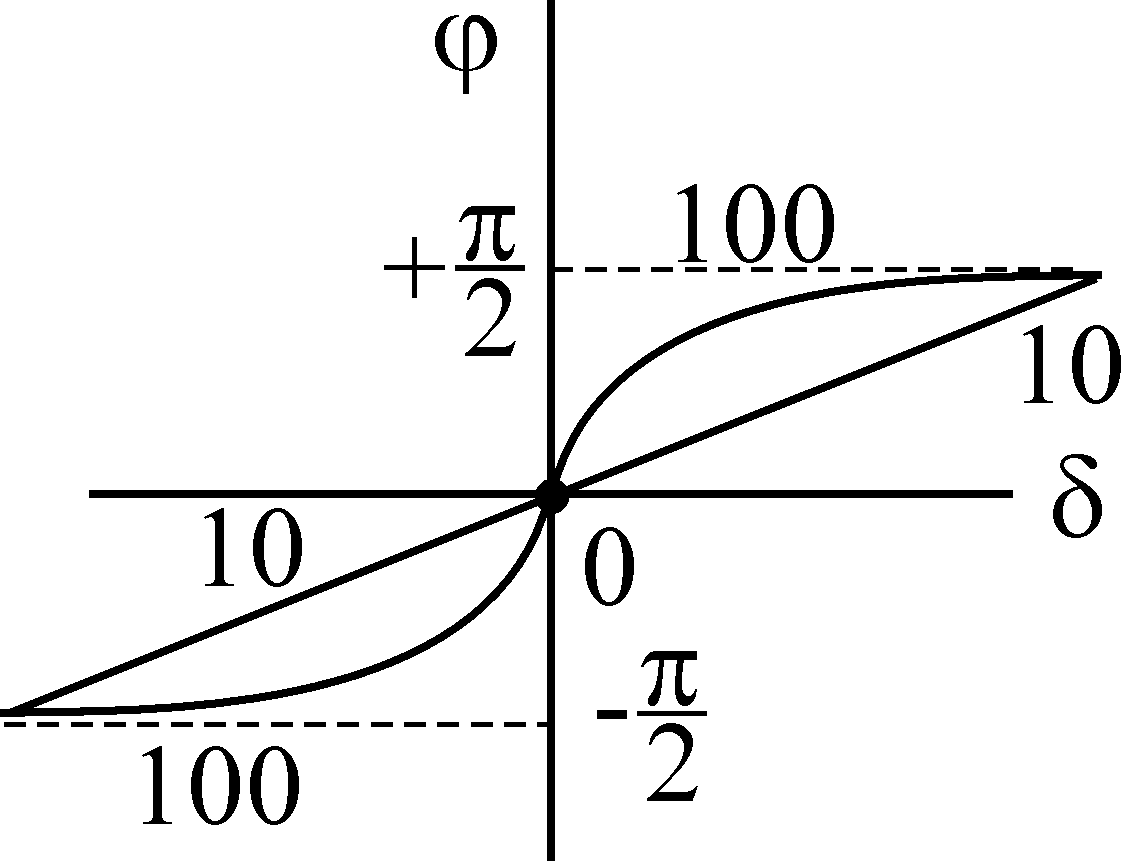
Q, а зависимости от обобщенной опции одинаковы для всех контуров.
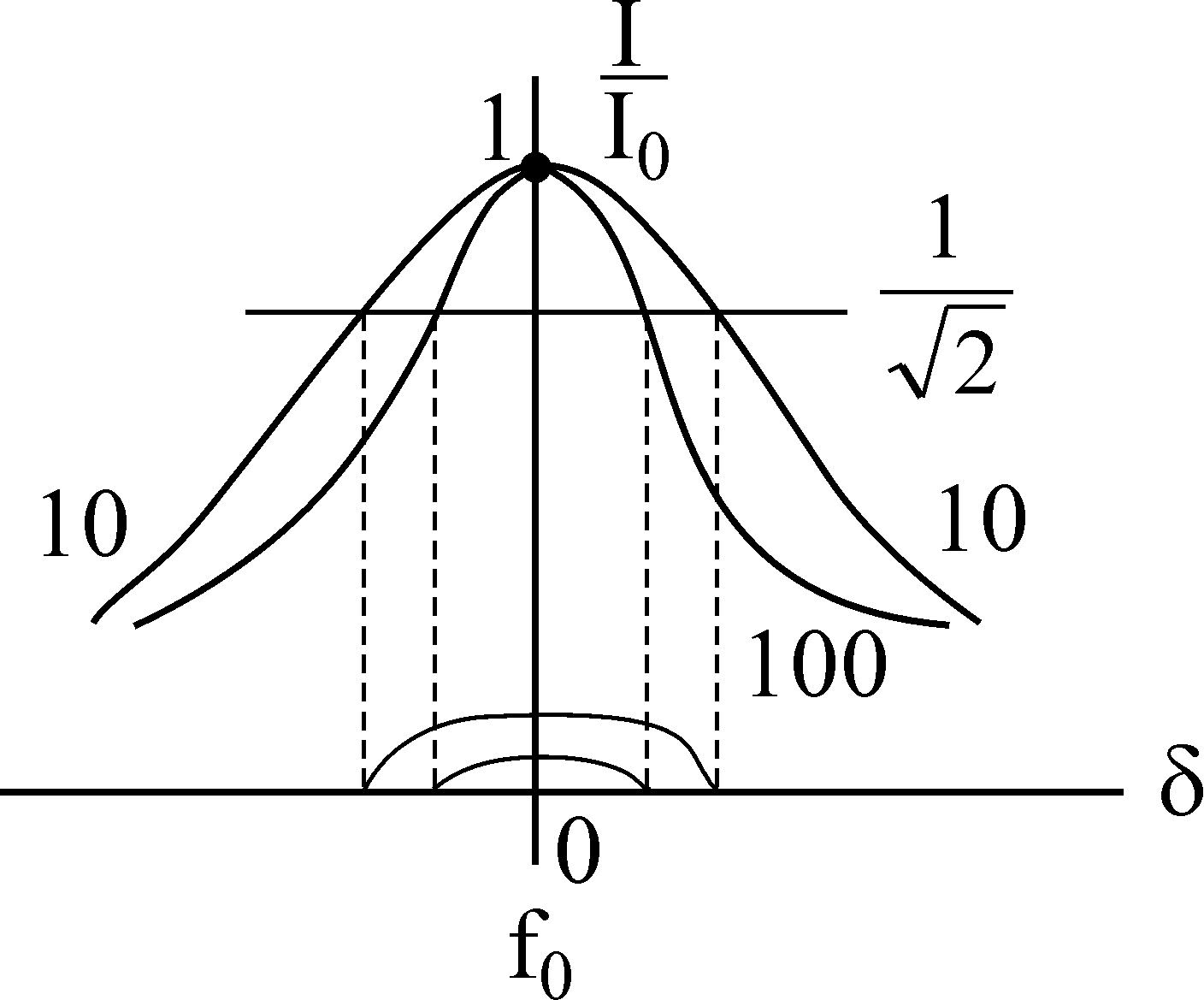
Полосу частот поблизости резонанса, на границах которой ток понижается до величины отпринято именоватьполосой пропускания резонансного тока.
Чем больше добротность, тем острее кривая и уже полоса пропускания
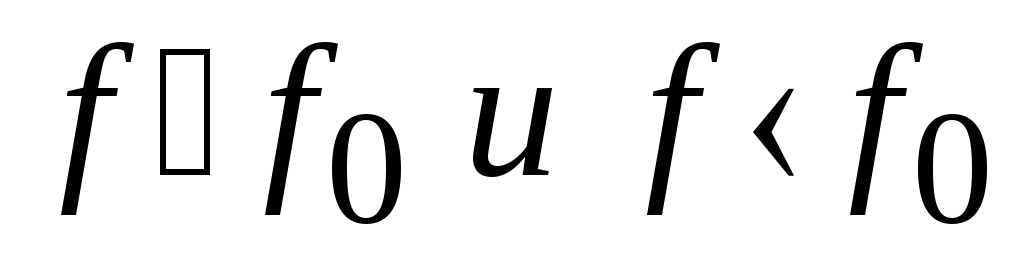
Векторные диаграммы при
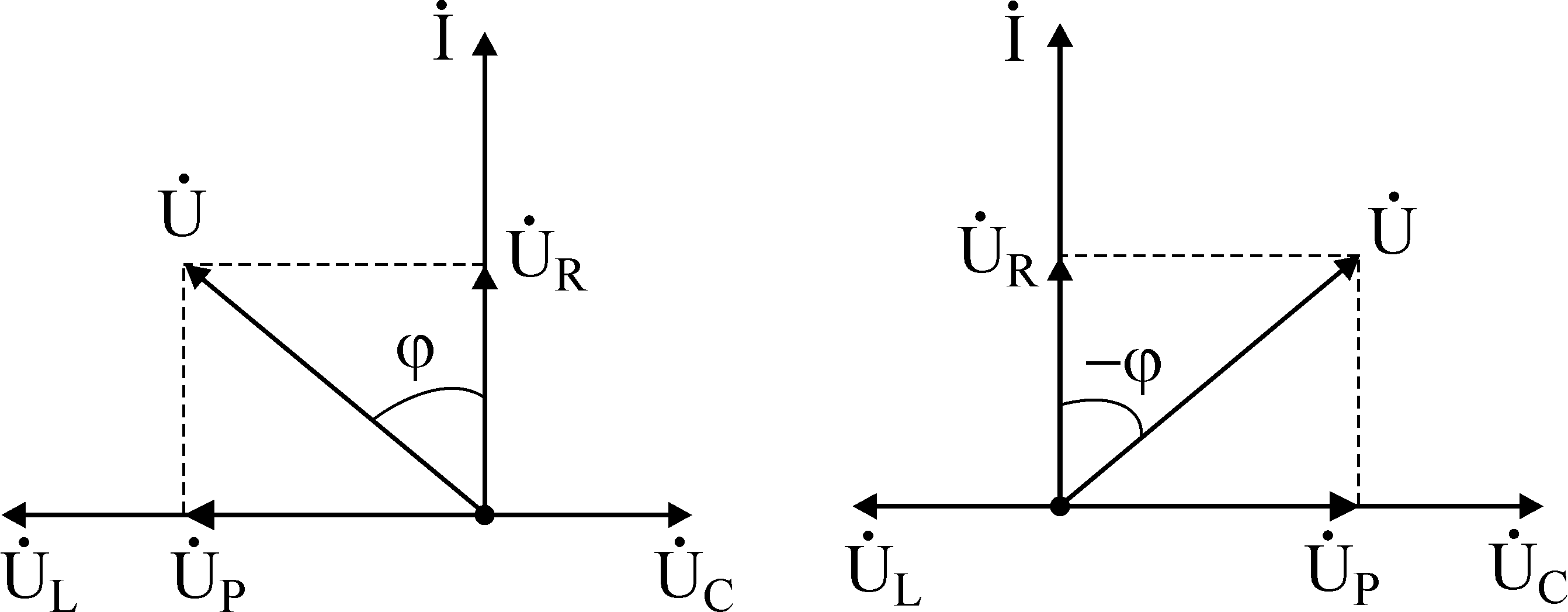
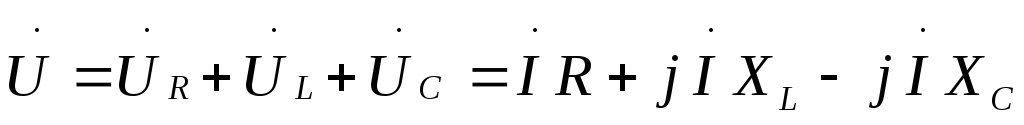
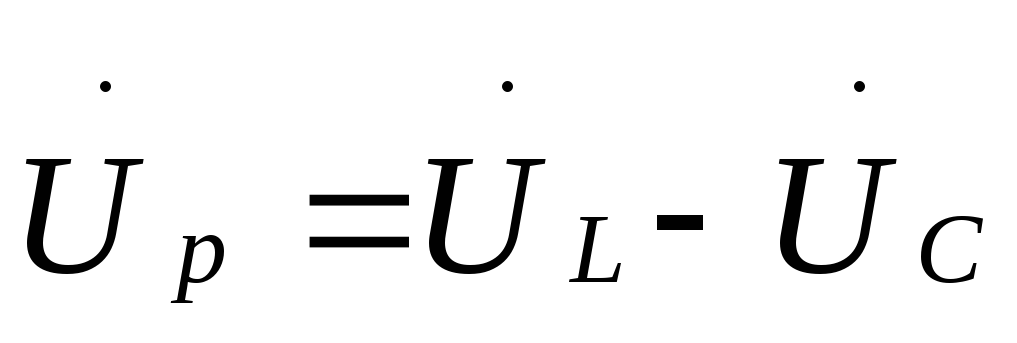
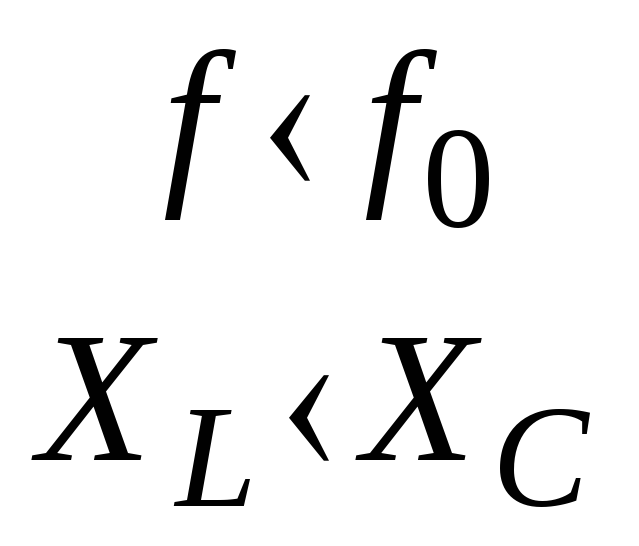
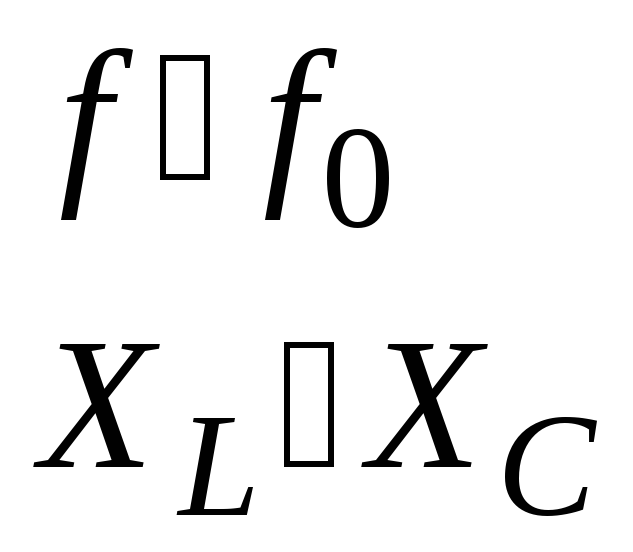
Если источник не безупречен и имеет своё внутреннее сопротивление, то это сопротивление практически добавляется к активному сопротивлению цепи и оказывает влияние на добротность и полосу пропускания контура. Чем больше внутреннее сопротивление источника, тем меньше добротность и обширнее полоса пропускания. Потому, исходя из убеждений сокращения полосы пропускания контура, выгоден источник с малым внутренним сопротивлением.
Если колебательный контур безупречен и в нём нет активного сопротивления, то общее сопротивление контура равняется к 0, а ток в цепи и добротность растут до бесконечности. Но в реальной цепи такового быть не может.
22.Условие резонанса токов
Резонанс токов наблюдается в цепях с параллельным включением L и C. Условием резонанса токов является равенство 0 реактивной проводимости цепи.
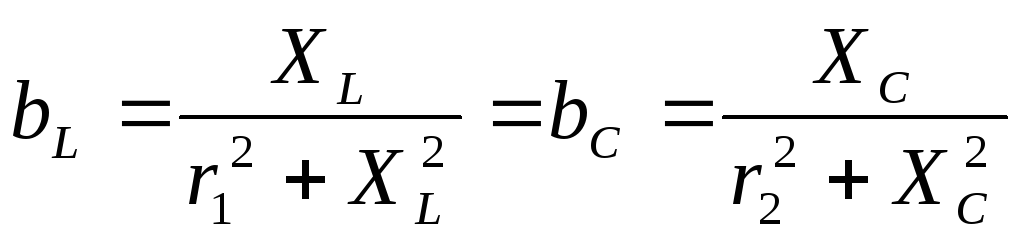
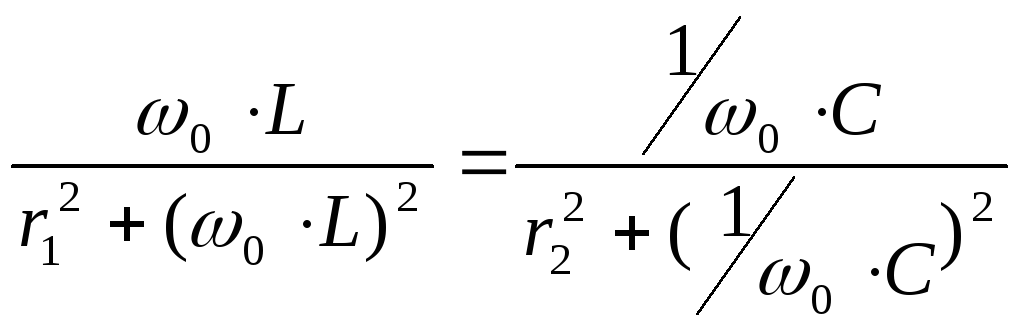
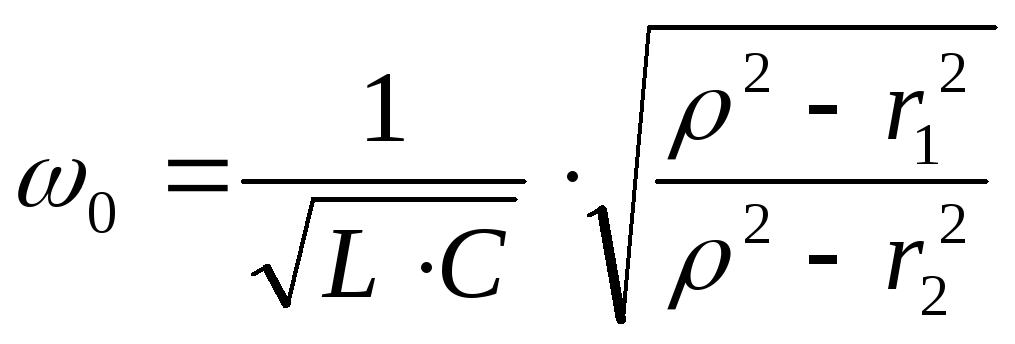
Это уравнения для более общего варианта. Резонанс в таком контуре не всегда вероятен. В идеализированном случае, когда активными качествами катушки и конденсатора третируют. Резонансная частота контура определяется формулой:
, ,.
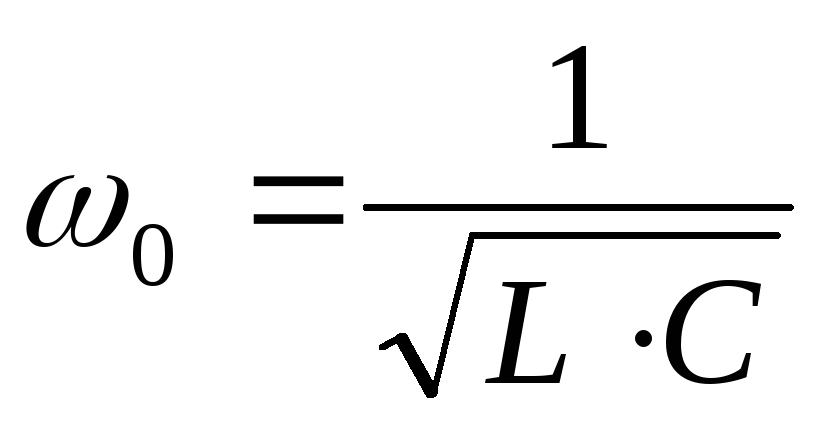
В момент резонанса ток добивается собственного малого значения и совпадает по фазе с напряжением.
Добротность – отношение модуля тока в реактивном элементе к модулю тока в неразветвлённой части схемы.
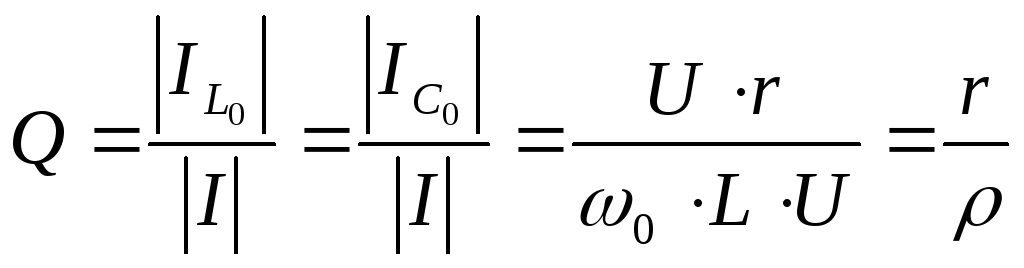
,
,
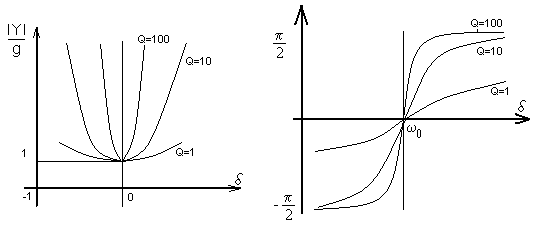
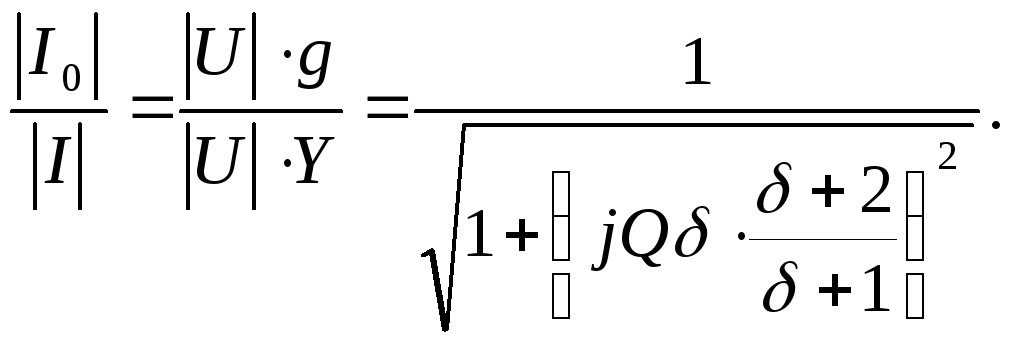
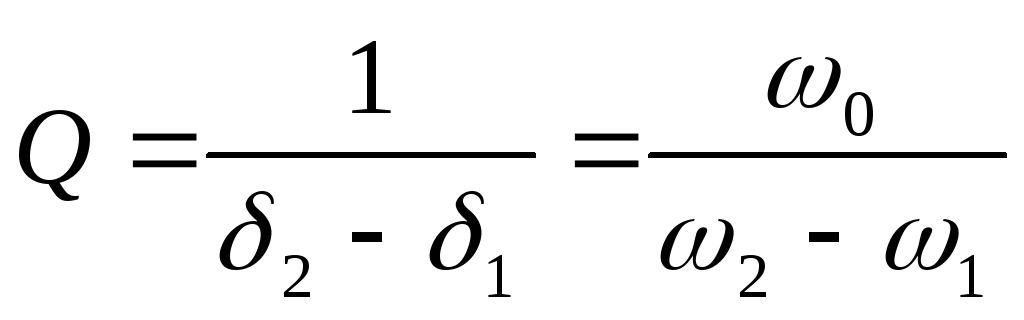
В отличие от последовательного колебательного контура исходя из убеждений сокращения полосы пропускания и колебательного контура выгоден источник тока с огромным Ri.(внутренним сопротивлением источника), так как чем меньше Ri , присоединяемое к параллельному контуру, тем ниже добротность и обширнее полоса пропускания.
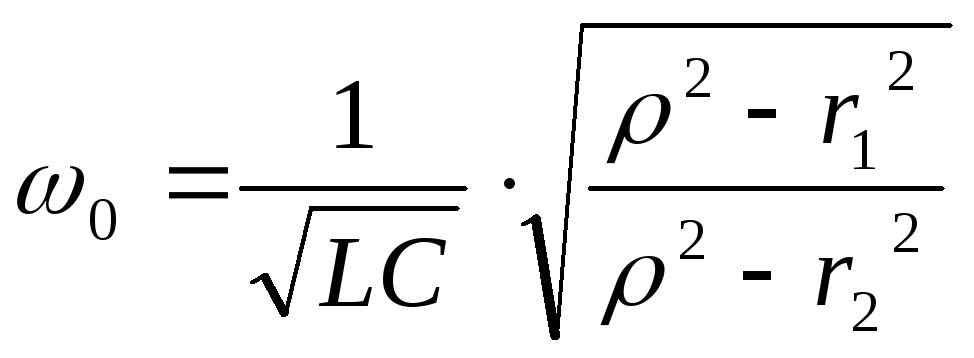
Анализируя полученную нами формулу для резонансной частоты резонанса тока, можно выделить 3 главных варианта:
Есть резонанс если иодного знака
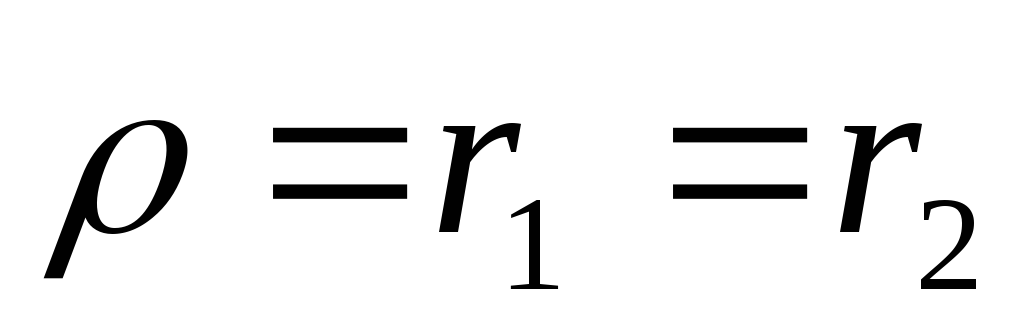
Безразличный резонанс
Резонанс в электрической цепи
ГОСТ
Начнём с главных определений.
Резонанс — это явление, при котором частота колебаний какой-нибудь системы возрастает колебаниями наружной силы.
Обязанные колебания, источником которых является наружняя сила, наращивают даже те колебания, амплитуда которых имеет достаточно маленькие значения. Наибольший резонанс с большей амплитудой вероятен конкретно при совпадении частот наружного воздействия и рассматриваемой системы.
Примером резонанса является раскачивание моста ротой боец. Частота шага боец, являющаяся по отношению к мосту примером принужденных колебаний, при всем этом синхронизирована и может совпасть с своей частотой колебаний моста. В итоге мост может разрушиться.
Электрический резонанс в физике считается одним из распространенных в мире физических явлений, без которого было бы неосуществимым, к примеру, телевидение и диагностика при помощи мед аппаратов.
Одними из более нужных видов резонанса в электрической цепи являются:
- резонанс токов;
- резонанс напряжений.
Появление резонанса в электрической цепи
Появлению резонанса в электрической цепи содействует резкое повышение амплитуды стационарных собственных колебаний системы при условии совпадения частоты наружной стороны воздействия и соответственной колебательной резонансной частоты системы.
Схема $RLC$ представляет электрическую цепь с соединенными последовательным либо параллельным образом элементами (резистора, индуктора, конденсатора). Название $RLC$ состоит из обычных знаков электрических частей: сопротивления, емкости, индуктивности.
Векторная диаграмма последовательной $RLC$-цепи представлена в одной из 3-х вариантов:
Готовые работы на аналогичную тему
Получить выполненную работу либо консультацию спеца по вашему учебному проекту Выяснить цена
- емкостной;
- активной;
- индуктивной.
В последней варианты резонанс напряжений появляется при условии нулевого сдвига фаз, и совпадении значений индуктивного и емкостного сопротивлений.
Резонанс напряжений
При последовательном соединении активного элемента $r$, емкостного $С$ и индуктивного $L$ в цепях переменного тока может появляться такое физическое явление, как резонанс напряжений. Колебания источника напряжения в данном случае будут равны по частоте колебаниям контура. При всем этом известна как полезность (к примеру, в радиотехнике) этого явления, так и нехорошие последствия (для электрических установок большой мощности), к примеру, при резком скачке напряжения в системах может быть появление неисправности либо даже пожара.
Резонанс напряжений обычно достигается 3-мя методами:
- подбором индуктивности катушки;
- подбором емкости конденсатора;
- подбором угловой частоты $w_0$.
При всем этом все значения емкости, частоты и индуктивности определяются с внедрением формул:
Частота $w_0$ считается резонансной. При условии неизменности в цепи и напряжения, и активного сопротивления $r$, сила тока при резонансе напряжения в ней окажется наибольшей и равной:
Это подразумевает полную независимость силы тока от реактивного сопротивления цепи. В ситуации, когда реактивные сопротивления $XC = XL$ по собственному значению будут превосходить активное сопротивление $r$, на зажимах катушки и конденсатора появится напряжение, значительно превосходящее напряжение на зажимах цепи.
Кратность превышения на зажимах емкостного и индуктивного элемента напряжения по отношению к сети определяется выражением:
Величина $Q$ охарактеризовывает резонансные характеристики контура, называясь при всем этом добротностью контура. Также резонансные характеристики характеризуются величиной $\frac$, другими словами — затуханием контура.
Резонанс токов через реактивные элементы
Резонанс токов возникает в электроцепях цепях переменного тока при условии параллельного соединения веток с разнохарактерными реактивными сопротивлениями. В резонансном режиме токов реактивная индуктивная проводимость цепи будет равнозначной ее своей реактивной емкостной проводимости, т.е. $BL = BC$.
Колебания контура, частота которых имеет определённое значение, в этом случае совпадают по частоте с источником напряжения.
Простейшей электроцепью, в какой мы смотрим резонанс токов, считается цепь с параллельным соединением конденсатора с катушкой индуктивности.
Так как сопротивления реактивности равнозначны по модулю, амплитуды токов $I_c$ и $I_u$ будут одинаковыми и сумеют достигать наибольшей амплитуды. На основании первого закона Кирхгофа $IR$ равен току источника. Ток источника, другими словами, протекает только через резистор. При рассмотрении отдельного параллельного контура $LC$, на резонансной частоте его сопротивление оказывается нескончаемо огромным: $ZL = ZC$. При установлении гармонического режима с резонансной частотой, в контуре наблюдается обеспечение источником установившейся определенной амплитуды колебаний, а мощность источника тока при всем этом расходуется только на пополнение утрат в активном сопротивлении.
Таким макаром, у последовательной $RLC$ цепи импеданс оказывается наименьшим на резонансной частоте и равным активному сопротивлению контура. В то же время, у параллельной $RLC$ цепи импеданс наибольший на резонансной частоте и считается равным сопротивлению утечки, практически также активному сопротивлению контура. С целью обеспечения критерий для резонанса силы тока либо напряжения, нужна проверка электрической цепи для предопределения ее всеохватывающего сопротивления либо проводимости. Кроме этого, её надуманная часть должна равняться к нулю.
Использование явления резонанса
Неплохой пример применения резонансного явления представляет электрический резонансный трансформатор, разработанный Николой Тесла ещё в 1891 году. Ученый проводил опыты на различных конфигурациях, состоящих в сочетании из 2-ух, а часто и 3-х резонансных электроцепей.
Термин «катушки Теслы» используют к высоковольтным резонансным трансформаторам. Устройства применяют при получении высокого напряжения, частоты переменного тока. Обыденный трансформатор нужен для действенной передачи энергии с первичной на вторичную обмотку, резонансный применяется для временного хранения электроэнергии.
Устройство отвечает за управление воздушным сердечником настроенного резонансно трансформатора с целью получения больших напряжений при малых значениях силы токов. Любая обмотка обладает емкостью и работает в качестве резонансного контура. Для произведения большего выходного напряжения первичный и вторичный контуры настраивают в резонанс вместе.