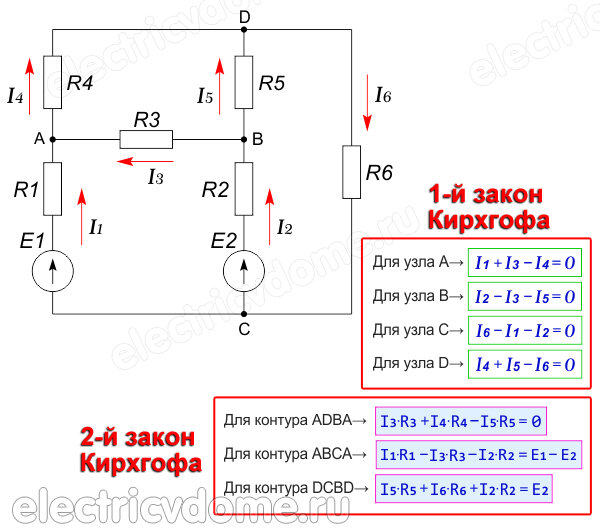
1-ый закон Кирхгофа для моментальных значений: алгебраическая сумма моментальных значений токов в узле равна нулю.
где k – число веток, соединенных в узле.
2-ой закон Кирхгофа для моментальных значений: алгебраическая сумма напряжений на элементах контура в данный момент времени равна алгебраической сумме ЭДС в том же контуре в тот же момент времени:
где k – порядковый номер напряжения;
p – порядковый номер ЭДС;
n – суммарное число частей в контуре;
m – число ЭДС в контуре.
1.11 Законы Кирхгофав всеохватывающей форме
Как показано в п. 1.3, синусоидальные функции времени можно представить в всеохватывающей форме. Осуществив схожий переход, можно записать законы Кирхгофа для цепи синусоидального тока в всеохватывающей форме.
1-ый закон Кирхгофа в всеохватывающей форме: алгебраическая сумма комплексов токов в узле электрической цепи равна нулю.
где k – число веток, соединенных в узле.
К примеру, для цепи, изображенной на рис.1.9, уравнение, составленное по первому закону Кирхгофа в всеохватывающей форме, имеет вид:
2-ой закон Кирхгофа в всеохватывающей форме: алгебраическая сумма комплексов напряжений в контуре равна алгебраической сумме комплексов ЭДС в этом же контуре.
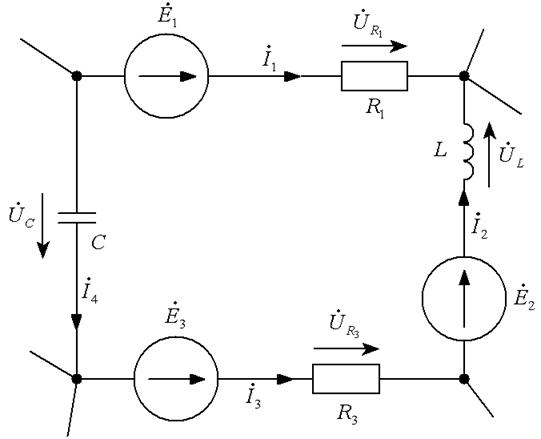
Для контура, изображенного на рис.1.10, уравнение, составленное по второму закону Кирхгофа в всеохватывающей форме, можно записать следующим образом:
где — комплекс падения напряжения на резисторе R1;
— комплекс падения напряжения на катушке индуктивности L;
— комплекс падения напряжения на резисторе R3;
— комплекс падения напряжения на конденсаторе С;
Пример 7
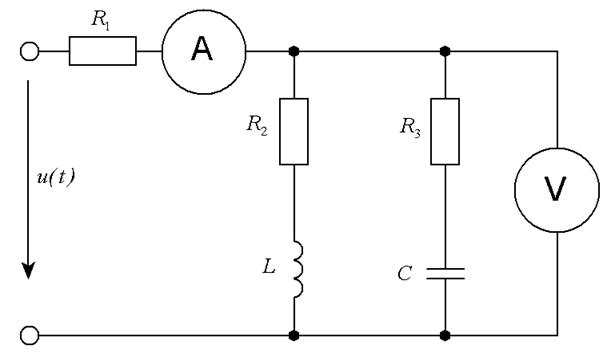
Найти комплексы токов в ветвях, показания устройств сложной цепи рис.1.11, выстроить векторную диаграмму токов и напряжений и осциллограмму напряжения на резисторе R1.
Решение
Угловая частота колебаний в цепи:
Определим всеохватывающие сопротивления всех частей цепи, при всем этом будем считать, что измерительные приборы безупречные, т.е. сопротивление амперметра равно нулю, а сопротивление вольтметра – бесконечности.
Всеохватывающее сопротивление резистора R1:
Всеохватывающее сопротивление резистора R2:
Всеохватывающее сопротивление катушки индуктивности L:
Всеохватывающее сопротивление резистора R3:
Всеохватывающее сопротивление конденсатора С:
Комплекс действующего значения напряжения :
Изобразим схему замещения цепи, на которой все элементы цепи и напряжение изменены их изображениями в всеохватывающей форме (рис.1.12).
Всеохватывающие сопротивления и соединены последовательно, означает их эквивалентное всеохватывающее сопротивление:
Всеохватывающие сопротивления и также соединены последовательно, означает их эквивалентное всеохватывающее сопротивление:
Цепь приобретет вид, показанный на рис.1.13.
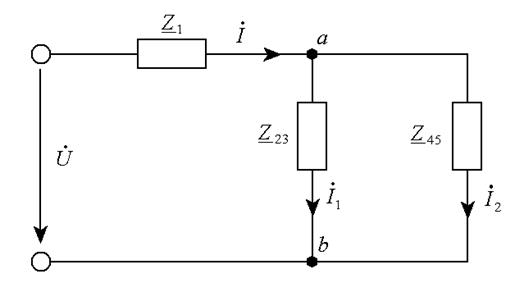
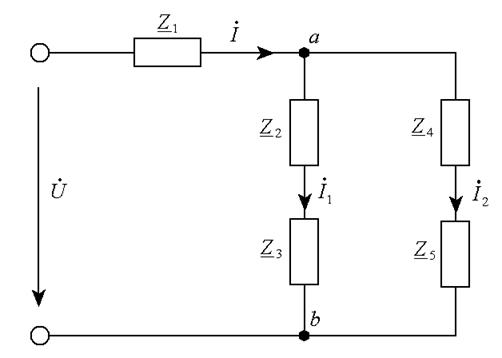
Ветки цепи, содержащие всеохватывающие сопротивления и соединены параллельно, поэтому, эквивалентное всеохватывающее сопротивление участка цепи между узлами a и b:
После преобразований цепь приобретет вид, показанный на рис.1.14.
Полное эквивалентное всеохватывающее сопротивление цепи рассчитывается как сумма всеохватывающих сопротивлений и :
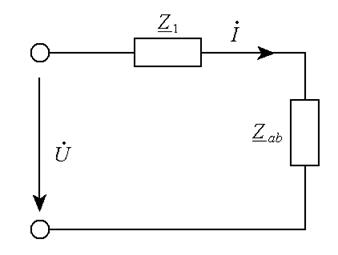
Определим комплекс действующего значения тока в неразветвленной части цепи:
Для того, дабы найти токи в ветвях, содержащих всеохватывающие сопротивления , и , , определим комплекс напряжения между узлами a и b.
Определим комплексы токов в ветвях:
Ток можно было получить, используя 1-ый закон Кирхгофа:
Определим показания устройств. Показания устройств представляют собой действующие значения измеряемых величин.
Амперметр указывает действующее значение тока, комплекс которого: . Действующее значение – это модуль комплекса тока, т.е. 11.74 (А).
Вольтметр указывает действующее значение напряжения между узлами a и b, комплекс которого: . Действующее значение – это модуль комплекса напряжения, т.е. 41.52 (В).
Векторная диаграмма токов представлена на рис.1.15.
Для построения векторной диаграммы напряжений определим комплексы напряжений на всех элементах цепи.
Комплекс напряжения на резисторе :
Комплекс напряжения на резисторе :
Комплекс напряжения на катушке индуктивности :
Комплекс напряжения на резисторе :
Комплекс напряжения на конденсаторе :
Векторная диаграмма напряжений представлена на рис.1.16.
Для построения осциллограммы напряжения на резисторе R1 нужно от отысканного нами ранее изображения этого напряжения в всеохватывающей форме перейти к ее аналитической форме записи.
Найдем амплитуду этого напряжения:
Аналитическая зависимость напряжения на резисторе R1 от времени будет иметь вид (с учетом того, что сек -1 ):
Согласно этой формуле осциллограмма будет иметь вид, представленный на рис.1.17.
Этапы развития населения земли: В последние годы определенную известность заполучили пробы.
Пример дизайна методической разработки: Методическая разработка — разновидность учебно-методического издания в помощь.