Нажмите либо коснитесь приведенных ниже примеров схем, дабы вызвать TINACloud, и изберите интерактивный режим DC, дабы проанализировать их в Вебе.
Получите дешевый доступ к TINACloud для редактирования примеров либо сотворения собственных схем
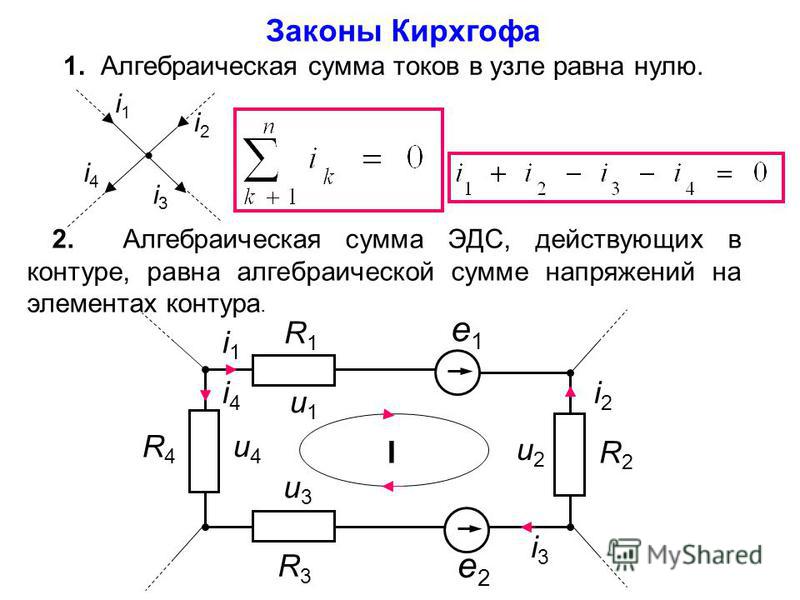
Многие схемы очень сложны, дабы их можно было решить, используя правила для последовательных либо параллельных схем либо способы преобразования в более обыкновенные схемы, описанные в прошлых главах. Для этих схем нам необходимы более общие способы решения. Более общий способ дается законами Кирхгофа, которые позволяют вычислять все напряжения и токи цепей по решению системы линейных уравнений.
Есть два Законы Кирхгофа, закон напряжения И текущий закон. Эти два закона могут быть применены для определения всех напряжений и токов в цепях.
Закон напряжения Кирхгофа (KVL) говорит, что алгебраическая сумма повышений напряжения и падений напряжения вокруг контура должна быть равна нулю.
Цикл в вышеприведенном определении значит замкнутый путь в цепи; другими словами путь, который покидает узел в одном направлении и ворачивается к тому же узлу из другого направления.
В наших примерах мы будем применять направление по часовой стрелке для циклов; но те же результаты будут получены при использовании направления против часовой стрелки.
Для использования KVL без ошибок, мы должны найти так называемое опорное направление. Опорное направление неведомого напряжения от точки к + — символ предполагаемых напряжений. Представьте для себя внедрение вольтметра. Вы положили бы положительный пробник вольтметра (обычно красный) на клемму + опоры компонента. Если реальное напряжение положительное, оно в том же направлении, что и мы, и наше решение, и вольтметр покажут положительное значение.
При выводе алгебраической суммы напряжений, мы должны присвоить символ плюс к тем напряжениям, где опорное направление совпадает с направлением петли, и отрицательными знаками в обратном случае.
Другой метод сконструировать закон напряжения Кирхгофа заключается в том, что приложенное напряжение последовательной цепи равно сумме падений напряжения на последовательных элементах.
Следующий маленький пример указывает внедрение закона напряжения Кирхгофа.
Отыскать напряжение на резисторе R2, беря во внимание, что напряжение источника, ВS = 100 В и это напряжение на резисторе R1 это V1 = 40 V.
Набросок ниже может быть сотворен при помощи TINA Pro версии 6 и выше, в какой инструменты рисования доступны в редакторе схем.
Решение с внедрением закона напряжения Кирхгофа: -VS + V1 + V2 = 0 либо VS V =1 + V2
Направьте внимание, что обычно мы не знаем напряжения резисторов (если мы не измеряем их), и нам необходимо применять оба закона Кирхгофа для решения.
Текущий закон Кирхгофа (KCL) говорит, что алгебраическая сумма всех токов, входящих и выходящих из любого узла в цепи, равна нулю.
Дальше мы даем символ + токам, выходящим из узла, и символ — токам, входящим в узел.
Вот основной пример, демонстрирующий действующий закон Кирхгофа.
Отыскать тока я2 если источник тока IS = 12 A, и я1 = 8 A.
Используя текущий закон Кирхгофа в обведенном узле: -IS + Я1 + Я2 = 0, поэтому: I2= ЯS — Я1 = 12 — 8 = 4 A, как вы сможете проверить при помощи TINA (следующий набросок).
В следующем примере мы будем применять как законы Кирхгофа, так и закон Ома, дабы высчитать ток и напряжение на резисторах.
На рисунке ниже вы заметите Напряжение Стрелка выше резисторы. Это новый компонент, доступный в Версия 6 TINA и работает как вольтметр. Если подключить его через компонент, стрелка определяет опорное направление (сопоставить с вольтметром, представьте размещения красного щупа в хвосте стрелки, а черный зонд на конце). При запуске анализа неизменного тока фактическое напряжение на компоненте будет отображаться на стрелке.
Дабы начать применять текущий закон Кирхгофа, мы лицезреем, что токи через все составляющие одинаковы, потому давайте обозначим этот ток через I.
Сейчас используя закон Ома: VS= I * R1+ I * R2+ I * R3
И отсюда ток цепи:
В конце концов напряжения на резисторах:
V1= I * R1 = 2 * 10 = 20 V; V2 = I * R2 = 2 * 20 = 40 V; V3 = I * R3 = 2 * 30 = 60 V
Те же результаты можно узреть на стрелках напряжения, просто запустив интерактивный анализ неизменного тока TINA.
В этой следующей, более сложной схеме мы также используем как законы Кирхгофа, так и закон Ома, но мы обнаруживаем, что мы более решаем линейную систему уравнений.
Полное количество независящих применений законов Кирхгофа в цепи — это число веток цепи, а полное количество неведомых (ток и напряжение каждой ветки) в два раза больше. Все же, также используя закон Ома на каждом резисторе и Из обычных уравнений, определяющих приложенные напряжения и токи, мы получаем систему уравнений, где число неведомых совпадает с числом уравнений.
Отыскать токи ветвления I1, I2, I3 в схеме ниже.
Система уравнений смотрится следующим образом:
Узловое уравнение для обведенного узла:
либо умножение на -1
Уравнения цикла (с внедрением направления по часовой стрелке) для цикла L1, содержащего V1, R1 и R3
и для цикла L2, содержащего V2, R2 и R3
Подставляя значения компонент:
Экспресс я1 используя узловое уравнение: I1 = -Я2 — Я3
потом подставьте его во 2-ое уравнение:
Экспресс я2 и подставим его в третье уравнение, из которого вы уже сможете высчитать I3:
Потому I3 = — 0.25 А; I2 = — (8-0.25 * 80) / 40 = 0.3 A и I1 = — (0.3-0.25) = — 0.05 А
Сейчас давайте решим те же уравнения с интерпретатором TINA:
| Sys I1, I2, I3 I1 + I2 + I3 = 0 -V1+I1*R1-I3*R3=0 I3*R3-I2*R2+V2=0 конец; I1 = [- 50m] I2 = [300m] I3 = [- 250m] |
В конце концов, давайте проверим Результаты с внедрением TINA:
Дальше, давайте проанализируем следующую, еще больше сложную схему и определим ее ответвления токами и напряжениями.
Нажмите / коснитесь схемы выше для анализа в режиме онлайн либо нажмите эту ссылку, дабы Сохранить в Windows
Обозначим неведомые напряжения и токи, добавив стрелки напряжения и тока к компонентам, также покажем петли (L1, L2, L3) и узлы (N1, N2), где мы будем применять уравнения Кирхгофа.
| Нажмите / коснитесь схемы выше для анализа в режиме онлайн либо нажмите эту ссылку, дабы Сохранить в Windows |
Вот набор Уравнения Кирхгофа для петель (с внедрением направления по часовой стрелке) и узлов.
Применяя закон Ома:
Это 9 неведомых и 9 уравнений. Самый обычной метод решить эту делему — применять TINA.
переводчик. Но, если мы обязаны применять ручные вычисления, отметим, что этот набор уравнений может быть просто сведен к системе из 5 неведомых методом подстановки последних 4 уравнений в уравнения цикла L1, L2, L3. Не считая того, добавив уравнения (L1) и (L2), мы можем убрать VIs , сводя задачку к системе уравнений 4 для неведомых 4 (IL, IR1 IR2, Is3). Когда мы отыскали эти токи, мы можем просто найти VL, VR1, VR2, и VR3 используя последние четыре уравнения (закон Ома).
Добавляя (L1) и (L2) мы получаем
После подстановки значений компонент решение этих уравнений идёт просто.
от L3 IR2 = 210 / 40 = 5.25 A (I)
Помножьте (IV) на –30 и добавьте к (III) 140 IL = -210 поэтому IL = — 1.5 А
Поменять яL в (IV) IR1 = 2 + (-1.5) = 0.5 A
Sys IL,IR1,IR2,Is3,VIs,VL,VR1,VR3,VR2
-IL-Is + IR1 = 0
-IR1 + IR2 + Is3 = 0
-Vs1 + VR3 + Вис-VL = 0
-Vis + VR1 + VR2 + Vs2 = 0
-Vs3 + VR2 + Vs2 = 0
VR1 = IR1 * R1
VR2 = IR2 * R2
VR3 = -IL * R3
VL = IL * RL
конец;
IL = [- 1.5]
IR1 = [500m]
IR2 = [5.25]
Is3 = [- 4.75]
= ВП [285]
VL = [- 30]
VR1 = [15]
VR2 = [210]
VR3 = [135]
Решение приведенной системы уравнений с внедрением интерпретатора:
| Sys Il, Ir1, Ir2, Is3 -Il + Ir1-2 = 0 -Ir1 + Ir2 + Is3 = 0 -120+110*Il+60+40*Ir2+30*Ir1=0 -40 * Ir2 + 210 = 0 конец; Ил = [- 1.5] Ir1 = [500m] Ir2 = [5.25] Is3 = [- 4.75] |
Мы также можем ввести выражения для напряжений и вынудить интерпретатора TINA высчитать их:
1-ый закон Кирхгофа
Создатель: Евгений Живоглядов.
Дата публикации: 14 августа 2013 .
Категория: Статьи.
Отдельные проводники электрической цепи могут быть соединены между собой последовательно, параллельно и смешанно. При всем этом последовательное и параллельное соединение проводников являются основными видами соединений, а смешанное соединение это их совокупа.
Последовательное соединение проводников
Последовательным соединением проводников именуется такое соединение, когда конец первого проводника соединен с началом второго, конец второго проводника соединен с началом третьего и т.д. (набросок 1).
Набросок 1. Схема последовательного соединения проводников
Общее сопротивление цепи, состоящее из нескольких последовательно соединенных проводников, равно сумме сопротивлений отдельных проводников:
Ток на отдельных участках последовательной цепи всюду одинаков:
Видео 1. Последовательное соединение проводников
Пример 1. На рисунке 2 представлена электрическая цепь, состоящая из 3-х последовательно включенных сопротивлений r1 = 2 Ом, r2 = 3 Ом, r3 = 5 Ом. Нужна найти показания вольтметров V1, V2, V3 и V4, если ток в цепи равен 4 А.
Сопротивление всей цепи
По закону Ома напряжение на зажимах цепи равно току цепи, умноженному на ее сопротивление:
Поэтому, вольтметр V, присоединенный к зажимам источника напряжения, покажет напряжение 40 В.
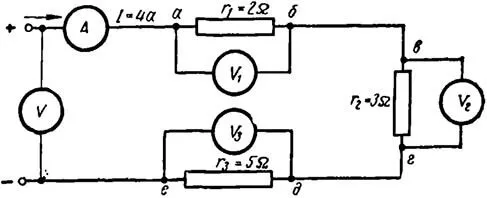
Набросок 2. Схема измерения напряжений на отдельных участках электрической цепи
В сопротивлении r1 при протекании тока будет падение напряжения:
Вольтметр V1, включенный между точками а и б, покажет 8 В.
В сопротивлении r2 также происходит падение напряжения:
Вольтметр V2, включенный между точками в и г, покажет 12 В.
Падение напряжения в сопротивлении r3:
Вольтметр V3, включенный между точками д и е, покажет 20 В.
Если вольтметр присоединить одним концом к точке а, другим концом к точке г, то он покажет разность потенциалов между этими точками, равную сумме падений напряжения в сопротивлениях r1 и r2 (8 + 12 = 20 В).
Таким макаром, вольтметр V, измеряющий напряжение на зажимах цепи и включенный между точками а и е, покажет разность потенциалов между этими точками либо сумму падений напряжения в сопротивлениях r1, r2 и r3.
Отсюда видно, что сумма падений напряжения на отдельных участках электрической цепи равна напряжению на зажимах цепи.
Так как при последовательном соединении ток цепи на всех участках одинаков, то падение напряжения пропорционально сопротивлению данного участка.
Пример 2. Три сопротивления 10, 15 и 20 Ом соединены последовательно, как показано на рисунке 3. Ток в цепи 5 А. Найти падение напряжения на каждом сопротивлении.
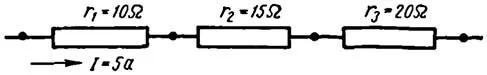
Набросок 3. Например 2
Общее напряжение цепи равно сумме падений напряжений на отдельных участках цепи:
Параллельное соединение проводников
Параллельным соединением проводников именуется такое соединение, когда начала всех проводников соединены в одну точку, а концы проводников – в другую точку (набросок 4). Начало цепи присоединяется к одному полюсу источника напряжения, а конец цепи – к другому полюсу.
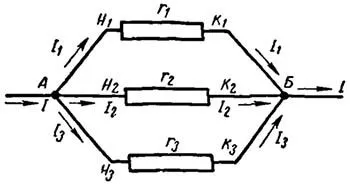 |
| Набросок 4. Схема параллельного соединения проводников |
Из рисунка видно, что при параллельном соединении проводников для прохождения тока есть некоторое количество путей. Ток, протекая к точке разветвления А, разливается дальше по трем сопротивлениям и равен сумме токов, уходящих от этой точки:
Если токи, приходящие к точке разветвления, считать положительными, а уходящие – отрицательными, то для точки разветвления можно написать:
другими словами алгебраическая сумма токов для хоть какой узловой точки цепи всегда равна нулю. Это соотношение, связывающее токи в хоть какой точке разветвления цепи, именуется первым законом Кирхгофа. Определение первого закона Кирхгофа может звучать и в другой формулировке, а конкретно: сумма токов втекающих в узел электрической цепи равна сумме токов вытекающих из этого узла.
Видео 2. 1-ый закон Кирхгофа
Обычно при расчете электрических цепей направление токов в ветвях, присоединенных к какой или точке разветвления, неопознаны. Потому для способности самой записи уравнения первого закона Кирхгофа необходимо до расчета цепи произвольно избрать так именуемые положительные направления токов во всех ее ветвях и обозначить их стрелками на схеме.
Пользуясь законом Ома, можно вывести формулу для подсчета общего сопротивления при параллельном соединении потребителей.
Общий ток, приходящий к точке А, равен:
Токи в каждой из веток имеют значения:
По формуле первого закона Кирхгофа
Таким макаром, при параллельном соединении возрастает не сопротивление, а проводимость.
Пример 3. Найти общее сопротивление 3-х параллельно включенных сопротивлений, если r1 = 2 Ом, r2 = 3 Ом, r3 = 4 Ом.
Найдем общее сопротивление цепи:
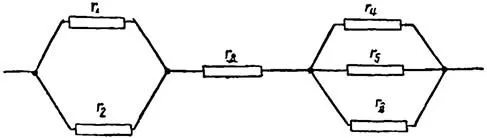
Набросок 6. Схема смешанного соединения проводников
Видео 3. Смешанное соединение проводников
Пример 7. Найти общее сопротивление смешанного соединения, представленного на рисунке 6, если