Электричеством пользуются всюду, и оно «было всегда» для подавляющего большинства людей. Но навряд ли многие думали о природе этого явления. Посреди главных электрических определений более сложными для осознания, невзирая на кажущуюся их простоту, являются «разность потенциалов» и «напряжение в цепи».
Понятие потенциала
Для того дабы электроны прошли по цепи, нужна энергия, способная привести их в движение по электрическому контуру. К примеру, в случае со статическим напряжением — это сила, производимая дисбалансом электрического заряда в предметах.
Школьный опыт с натиранием эбонитовой палочки об шерсть иллюстрирует создание излишка электронов в эбоните (отрицательный заряд) и недостаток электронов в шерсти (положительный заряд) при издержек механической энергии на натирание.
Между изолированными электродами этот дисбаланс проявляется только в притяжении наэлектризованных предметов друг к другу. Если же их соединить проводником, то электроны пойдут через него от эбонита к шерсти, компенсируя недостаток.
Это и есть электрический ток в цепи, а степень электризации тел есть величина, именуемая потенциалом. Упрощённо для осознания того, что именуется напряжением, можно рассматривать данную величину как разницу потенциалов между предметами.
Гидравлическая модель

Процесс получения зарядов в натираемых друг об друга материалах аналогичен заполнению бака воды на высоте из свободного резервуара. В сопоставлении с зеркалом открытого бассейна ёмкость с водой, расположенную выше, можно рассматривать как аккумулятор энергии. Гравитационные силы наделяют воду на возвышении возможной способностью опустошить бак при разгерметизации. Если соединить трубой описываемые ёмкости, вода под действием тяжести создаст поток в ней, освобождая энергию, скопленную от подготовительной закачки, ввысь.
Подобно недвижной воды в высочайшем резервуаре, энергия, скопленная в натёртых предметах, именуется возможной — она имеет возможность (потенциал) быть реализованной движением электронов по проводнику.
В случае со статическим напряжением то, что именуется напряжением, можно выразить так: это единица работы, нужная для перемещения единицы заряда из 1-го места в другое с преодолением силы, которая пробует сохранить потенциалы уравновешенными.
Мера возможной энергии (нужной работы) на единицу заряда для перемещения его по проводнику — так будет смотреться описание того, что такое напряжение как определение, применимое к электрическим цепям.
Список физических величин, которыми обрисовывают явление напряжения:
- разность потенциалов — измеряется в вольтах (В);
- электрический заряд — Кулон (Кл);
- работа по перемещению заряда — Джоуль (Дж).
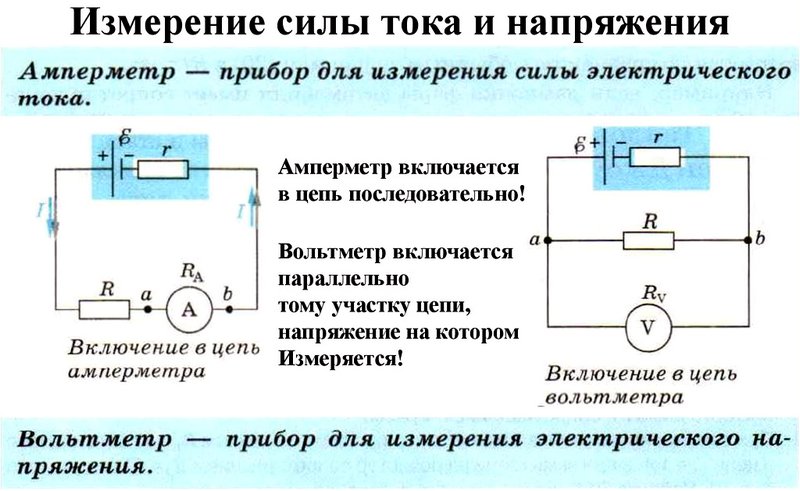
Для электрических цепей с гальваническими источниками питания, сетей переменного напряжения либо электростатических явлений нет различия, в чём измеряется электрическое напряжение. Во всех случаях показатель рассматривается как разность потенциалов и определяется в вольтах. Единицу измерения можно представить так: 1В=1Дж/1Кл. Устройство для измерения напряжения именуют вольтметром.
Измерения в цепи
Питание во наружном контуре создаётся источником, выполняющим функцию насоса (в аналогии с водяными резервуарами). Оно принудительно обеспечивается работой электрического поля во внутренней цепи в итоге преобразования хим реакций в гальванических элементах либо механической энергии в генераторах.
Во наружных электрических цепях движение заряда происходит естественным образом между потенциалами и сопровождается энергопотерями на обеспечение этого движения.
В этой связи источник неизменного питания должен безпрерывно поставлять нужную энергию на поддержание разности потенциалов на 2-ух концах наружной цепи, создавая высочайшее электрическое давление (по аналогии с гидравлическим примером).
Когда заряд перемещается через наружный контур, он сталкивается с разными элементами схемы, любой из которых является устройством по преобразованию энергии. Это могут быть лампочки, движки, нагревательные элементы. К примеру, в лампе накаливания энергия электрического потенциала преобразуется в световое и термическое излучение. Таким макаром, происходит утрата потенциала, другими словами он будет различен до нагрузки (лампа) и после неё. Утраты электрического потенциала при прохождении через элементы контура именуют падением напряжения. Это один из важных характеристик для контроля работы устройств в цепи.
Список главных законов и формул электрического напряжения, описывающих явление в цепях, смотрится так:
- Формула расчёта напряжения: U=A/q, где q — заряд (Кл), A — работа по перенесению заряда (Дж).
- Закон Ома: U=IR, где I — сила тока в цепи, R — сопротивление проводника, на концах которого замеряется напряжение.
- Разность потенциалов на последовательных элементах цепи: U=U1+U2+U3+…+Un.
Принципиально осознавать, что напряжение ни при каких обстоятельствах не может быть мерой тока. Разность потенциалов и электрический ток — два слабо связанных явления. На теоретическом уровне, может быть сделать ток без напряжения путём недлинного замыкания в вакууме, а оборотным примером может служить обыденный заряженный конденсатор. Предположение о том, что ток имеет напряжение, — распространённое заблуждение. Это стоит держать в голове для осознания физики описываемых явлений.
Базы электроники. Урок №2: Ток и напряжение в электрической цепи
На прошлом уроке мы научились определять мультиметром напряжение, ток и сопротивление, также собрали первую схему на макетной плате. Сейчас мы расширим схему, добавив еще несколько резисторов. Как это воздействует на ток и напряжение в схеме? Давайте проверим!
Мы начнем с сотворения макета в согласовании со следующей схемой:
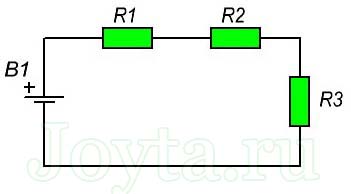
B1 – это как и раньше наша кассета из 4 пальчиковых батареек типа АА, любая номиналом 1,5 вольт (дальше для простоты будем гласить как об одной батареи)
- R1 – резистор 22кОм (полосы — красный/красный/оранжевый/золотой)
- R2 – резистор 10кОм (полосы — карий/черный/оранжевый/золотистый)
- R3 – резистор 2,2кОм (полосы — красный/красный/красный/золотой)
Найти сопротивления резисторов по цветным полоскам можно тут.
Силиконовый коврик для пайки
Размер 55 х 38 см, вес 800 гр.
Направьте внимание, что каждый резистор обозначается одним и этим же эмблемой (R), меняется только стоящая за ним цифра. Как обозначались бы резисторы на схеме, если все 3 имели однообразное сопротивление? Так же, как и на схеме выше – каждый элемент будет иметь свой свой номер!
Правило чтения электронных схем – каждый элемент 1-го и такого же типа имеет один и тот же буквенный знак, отличающийся только порядковым номером.
Давайте вернемся к нашей схеме. Если вы уже подобрали резисторы, то давайте построим макет на макетной плате. Наш макет смотрится так:

Давайте, для начала, выясним, какое напряжение для нашей схемы обеспечивает батарея. Возьмите мультиметр, приготовленный для измерения напряжения, с регулятором, установленным на 20В (почему таковой спектр, как приготовить мультиметр и как им воспользоваться описано в уроке №1). Приложим оба щупа мультиметра к выводам нашей батареи B1:
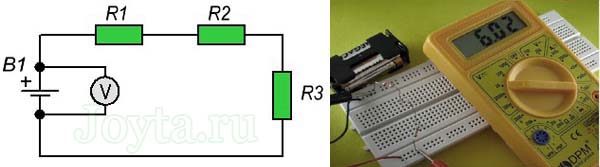
Наша батарея выдает напряжение 6,02В. Сейчас измерим фактическое сопротивление всех 3-х резисторов (R1, R2, R3). Мы получили следующие результаты: 21,9кОм, 10кОм и 2,23кОм соответственно.
Какова будет сила тока в цепи? Для начала, попробуем посчитать:
Знак U значит напряжение, которое обеспечивает наша батарея, а R — это сумма сопротивлений всех электронных компонент, другими словами резисторов, и потому:
I = U / (R1 + R2 + R3)
I = 6,02В / (21,9кОм + 10кОм + 2,23кОм)
I = 6,02В / 34,13кОм
I = 6,02В / 34130 Ом
I = 0,000176А = 176мкA
Сейчас измерим мультиметром фактический ток:

Мы сделали измерение, приложив красный щуп мультиметра к красному проводу батареи, а черный щуп к выводу первого резистора.
Как видно на рисунке, фактический ток цепи равен току, который мы высчитали ранее: 176мкA.
Можно испытать измерить ток, подключив мультиметр в другое место схемы, к примеру, между резисторами либо между резистором R3 и черным проводом батареи – уверяем, что вы получите один и тот же итог. Сила тока в нашей схеме будет одинакова.
Вы помните наше предшествующее сопоставление электрического тока с потоком воды? Наш „поток воды” никуда не девается, вытекает из 1-го вывода батареи, последовательно проходит через все резисторы и добивается второго вывода батареи. Потому сила тока (поток воды) в схеме одинакова.
Давайте проследим, что все-таки происходит с напряжением в нашей схеме. Мы знаем, что батарея выдает нам напряжение 6,02В, а сила тока всей цепи составляет 176мкA. Можно ли вычислить какое падение напряжения происходит на каждом из резисторов? Естественно! Поможет нам в этом закон Ома для участка цепи:
- падение напряжения на резисторе R1(22кОм) равно:
U = I x R
U = 176мкA x 21,9кОм
U = 0,000176А x 21900 Ом
U = 3,85В
- падение напряжения на резисторе R2 (10кОм) равно:
U = I x R
U = 176мкА x 10кОм
U = 0,000176А x 10000 Ом
U = 1,76В
- падение напряжения на резисторе R2 (2,2кОм) равно:
U = I x R
U = 176мкA x 2,23кОм
U = 0,000176А x 2230 Ом
U = 0,39В
Из приведенных расчетов можно увидеть, что чем больше сопротивление резистора, тем выше на нем падение напряжения.
Сейчас поглядим, какое напряжение мы получим, прикладывая щуп мультиметра к каждому из резисторов:
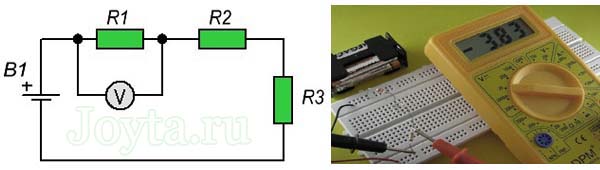
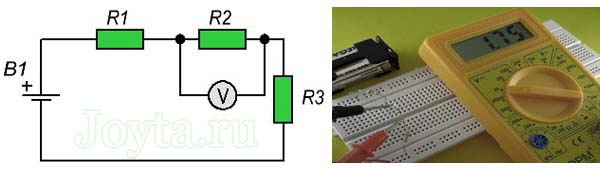
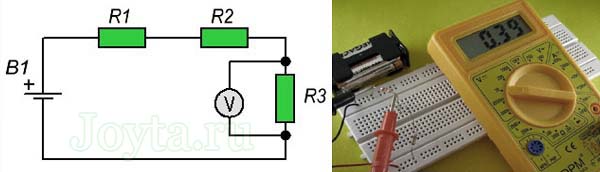
На каждом резисторе падение напряжения составило:
Сумма падений напряжений на отдельных резисторах практически равна напряжению батареи. На теоретическом уровне напряжение UB1 и UR1 + UR2+ UR3 должны быть равны, но на практике, это не всегда случается так. Почему? В этом случае разница появляется, возможно, из-за некорректности измерения мультиметра.
Помните также, что не только лишь сами резисторы оказывают сопротивление току. Сопротивление (хотя и маленькое) также есть и у проводов, через которые протекает ток.
Так либо по другому, мы экспериментально пришли ко второму правилу Кирхгофа, в каком говорится о том, что сумма падения напряжения на всех участках цепи равна источнику питания этой цепи.
Элементы цепей переменного напряжения
Всем хорошего времени суток! В прошлой статье я сказал о переменном напряжении и его параметрах. Данная статья, на самом деле, является продолжение предшествующей и затронет вопросы цепей переменного напряжения и тока, также их воздействие на сопротивление, ёмкость и индуктивность в разных сочетаниях. Начнём с простых цепей с синусоидальным переменным напряжением
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Сопротивление в цепи при переменном напряжении
Цепи переменного напряжения с сопротивлением является самыми ординарными и более нередко встречающимися, потому начнём с них.
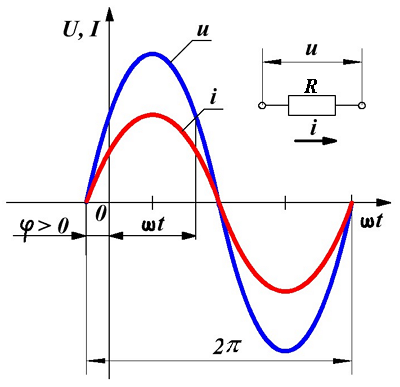
Переменное синусоидальное напряжение и ток в сопротивлении.
Допустим, что на сопротивление R подали переменное напряжение u, тогда, согласно с законом Ома, через данное сопротивление потечёт электрический ток i
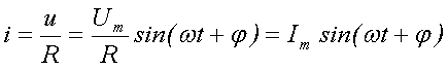
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
ω – угловая частота,
φ – исходная фаза
Таким макаром, действующее I и среднее значение Icp переменного тока будут определяться следующими выражениями
Так как, напряжение и ток, в цепи с сопротивлением имеют одинаковую исходную фазу, другими словами, происходит совпадение фаз и достижение амплитудных значений напряжения Um и тока Im происходит сразу.
Выражение «совпадение фаз» связанно с понятием фазового сдвига ψ, которое определяет разность исходных фаз 2-ух синусоид одинаковой частоты. Поэтому, фазовый сдвиг между напряжением и током при активном сопротивлении будет равен нулю
где φu – исходная фаза напряжения,
φi – исходная фаза тока.
Для оценки энергетических черт ввели понятие мощности, в цепях переменного напряжения существует несколько мощностных черт. Какой-то из них является моментальная мощность Рm, определяемая, как произведение моментальных значений напряжения и тока
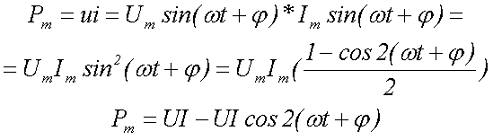
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
U – действующее значение переменного напряжения,
I – действующее значение переменного тока.
Таким макаром, моментальная мощность Рm меняется с двойной частотой по сопоставлению с частотой напряжения и тока и колеблется в границах от 0 до 2UI.
Очередной энергетической чертой является среднее значение мощности за период Р либо активная мощность, которая определяется следующим выражением
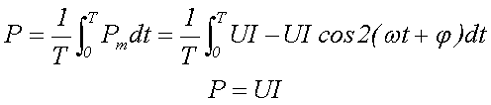
где Рm – моментальная мощность,
U – действующее значение переменного напряжения,
I – действующее значение переменного тока.
Индуктивность в цепи при переменном напряжении
Следующий элемент, который я рассмотрю, будет индуктивный элемент, характеризующийся тем, что в нём появляется ЭДС самоиндукции.
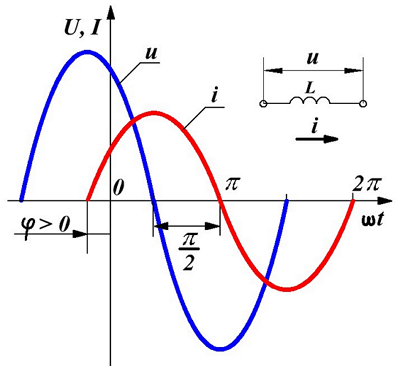
Переменное синусоидальное напряжение и ток в индуктивности.
При подаче переменного напряжения u на индуктивность L, в ней возникнет ЭДС самоиндукции
Тогда при условии, что сопротивление отсутствует R = 0, а разность потенциалов будет равна моментальному значению напряжения u, получим
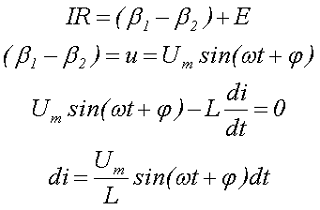
где (β1 – β2) – разность потенциалов,
Е – ЭДС самоиндукции,
Um – амплитудное значение переменного напряжения,
L – величина индуктивности,
ω – угловая частота,
φ – исходная фаза
Тогда проинтегрировав получившееся выражение, получим значение моментального тока
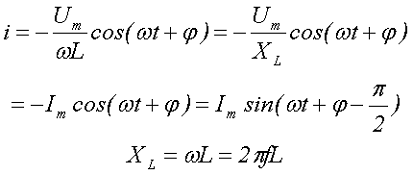
где Im – амплитудное значение переменного тока,
ω – угловая частота,
L – величина индуктивности,
f – частота переменного напряжения (тока),
XL – индуктивное сопротивление либо реактивное сопротивление индуктивности.
Как видно из получившегося выражения ток i в индуктивности опаздывает от напряжения на угол π/2 либо 90°. Другими словами фазовый сдвиг составит
Оценим секундную мощность Pm в индуктивности при переменном напряжении
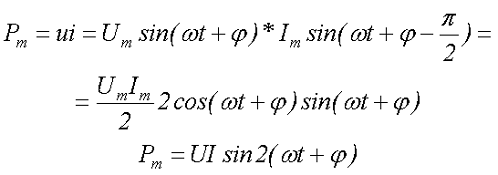
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
U – действующее значение переменного напряжения,
I – действующее значение переменного тока.
Таким макаром, моментальная мощность колеблется с двойной частотой по сопоставлению с частотой напряжения (тока) и амплитудой UI.
Рассчитаем активную (среднее значение) мощность Р за период. Для этого нужно проинтегрировать значение моментальной мощности за весь период, а потом поделить на продолжительность периода
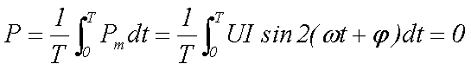
Как видно активная мощность на индуктивности не выделяется, другими словами она затрачивается, но за счёт ЭДС самоиндукции происходит её компенсация.
Значимым параметром индуктивности при прохождении через неё переменного тока является энергия магнитного поля индуктивности WL, которая рассчитывается по формуле
где Im – амплитудное значение переменного тока,
I – действующее значение переменного тока,
Как видно из получившегося выражения, повторяющиеся конфигурации энергия магнитного поля происходят с двойной частотой по сопоставлению с частотой напряжения (тока) через катушку и значением от 0 до LI 2 .
Ёмкость в цепи при переменном напряжении
Третьим элементом, который я рассмотрю, будет емкость, которая характеризуется тем, что в ней происходит скопление электроэнергии.
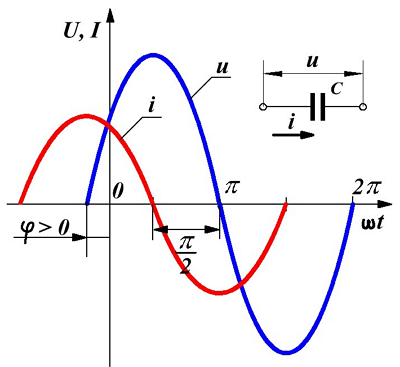
Переменное синусоидальное напряжение и ток в ёмкости.
Как понятно напряжение на конденсаторе определяется по формуле
где q – величина заряда,
С – ёмкость конденсатора.
С учётом того что, вся ЭДС переменного напряжения Е = u приложена к конденсатору и сопротивление равно нулю R = 0, согласно закона Ома для полной цепи получим
Другими словами величина заряда q будет изменяться пропорционально изменению напряжения u, а поэтому будет протекать электрический ток i.
Секундное значение электрического тока i при переменном напряжении на конденсаторе находится в зависимости от конфигурации электрического заряда dq за каждый период времени dt, тогда
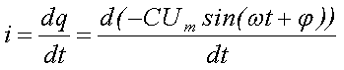
Проинтегрировав данное выражение получим
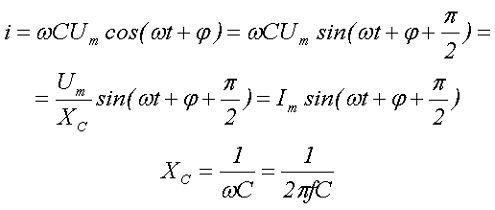
где Im – амплитудное значение переменного тока,
ω – угловая частота,
С – величина ёмкости,
f – частота переменного напряжения (тока),
XС – ёмкостное сопротивление либо реактивное сопротивление ёмкости..
Фазовый сдвиг между напряжением и электрическим током в ёмкости при переменном напряжении составит
Другими словами напряжение в этом случае отстаёт от тока на 90°.
Определим энерго свойства в ёмкости. Секундное значение мощности Pm в ёмкости при переменном напряжении
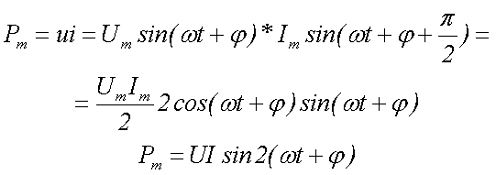
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
U – действующее значение переменного напряжения,
I – действующее значение переменного тока.
Таким макаром, значение моментальной мощности в ёмкости аналогично значению моментальной мощности в индуктивности, другими словами колебания происходят с двойной частотой по сопоставлению с частотой напряжения (тока) и амплитудой UI.
В отличии от индуктивности, в ёмкости энергия запасённая в конденсаторе определяется напряжением
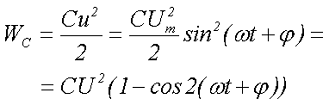
где Um – амплитудное значение переменного напряжения,
U – действующее значение переменного напряжения,
Таким макаром, энергия электрического поля в конденсаторе меняется с двойной частотой по сопоставлению с частотой напряжения (тока) и может принимать значение от 0 до CU 2 .
На сей день всё. В следующей статье я расскажу о параметрах разных соединений сопротивления, индуктивности и ёмкости при переменном напряжении и токе.
Теория это отлично, но нужно отрабатывать это всё фактически ПОПРОБЫВАТЬ МОЖНО Тут