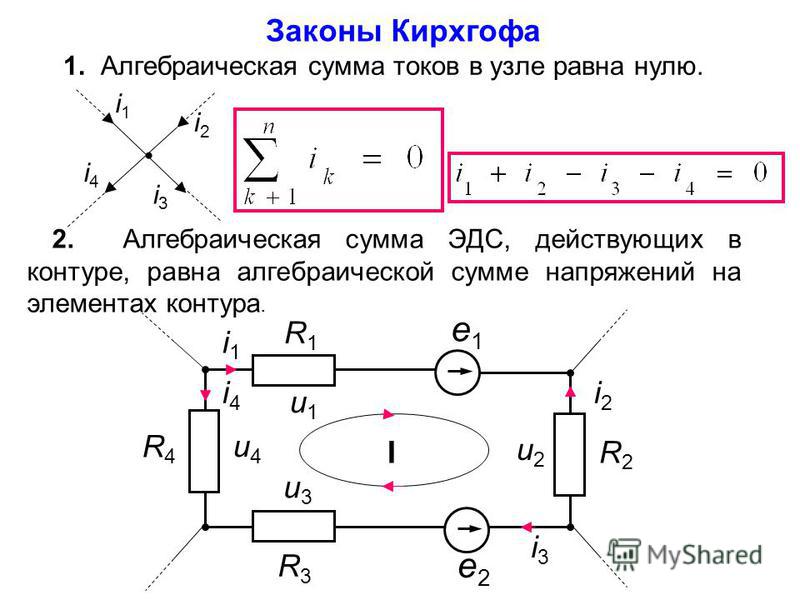
се электрические цепи подчиняются первому и второму законам (правилам) Кирхгофа.
1-ый закон Кирхгофа можно сконструировать двойственно:
1) алгебраическая сумма токов, подтекающих к хоть какому узлу схемы, равна нулю;
2) сумма подтекающих к хоть какому узлу токов равна сумме утекающих от узла токов.
Применительно к рис. 2.8, если подтекающие к узлу токи считать положительными, а утекающие — отрицательными, то согласно первой формулировке
На физическом уровне 1-ый закон Кирхгофа значит, что движение зарядов в цепи происходит так, что ни в каком из узлов они не накапливаются.
Если на уровне мыслей рассечь всякую схему случайной плоскостью и все находящиеся по одну сторону от нее рассматривать как некоторый большой «узел», то алгебраическая сумма токов, входящих в этот «узел», будет равна нулю.
2-ой закон Кирхгофа также можно сконструировать двойственно:
1) алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль такого же контура:
(в каждую из сумм надлежащие слагаемые входят со знаком плюс, если они совпадают с направлением обхода контура, и со знаком минус, если они не совпадают с ним);
2) алгебраическая сумма напряжений (не падений напряжения!) вдоль любого замкнутого контура равна нулю:
Для периферийного контура схемы рис. 2.9
Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом нраве конфигурации во времени токов и напряжений.
Создадим два замечания: 1) запись уравнения по второму закону Кирхгофа в форме (2.4) может быть получена, если обойти какой-нибудь контур некоторой схемы и записать выражение для потенциала случайной точки этого контура через потенциал этой же точки (взяв ее за начальную при обходе) и падения напряжения и ЭДС; 2) при записи уравнений по второму закону Кирхгофа в форме (2.4а) напряжения Uklучастков цепи содержат в себе и падения напряжения участков, и имеющиеся на этих участках ЭДС.
1-ое правило
Сколько тока втекает в узел, столько из него и вытекает. i2 + i3 = i1 + i4
1-ое правило Кирхгофа говорит, что алгебраическая сумма токов в каждом узле хоть какой цепи равна нулю. При всем этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:
Другими словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.
2-ое правило
2-ое правило Кирхгофа (правило напряжений Кирхгофа) говорит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих хоть какому замкнутому контуру цепи, равна алгебраической сумме ЭДС веток этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:
для неизменных напряжений
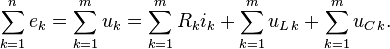
для переменных напряжений
Это правило вытекает из 3-го уравнения Максвелла, в личном случае стационарного магнитного поля.
Другими словами, при полном обходе контура потенциал, изменяясь, ворачивается к начальному значению. Личным случаем второго правила для цепи, состоящей из 1-го контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура необходимо избрать положительное направление обхода контура. При всем этом падение напряжения на ветки считают положительным, если направление обхода данной ветки совпадает с ранее избранным направлением тока ветки, и отрицательным — в неприятном случае (см. дальше).
Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом нраве конфигурации во времени токов и напряжений.
Особенности составления уравнений для расчёта токов и напряжений
Если цепь содержит узлов, то она описывается уравнениями токов. Это правило может применяться и для других физических явлений (например, система трубопроводов воды либо газа с насосами), где осуществляется закон сохранения частиц среды и потока этих частиц.
Если цепь содержит веток, из которых содержат источники тока ветки в количестве , то она описывается уравнениями напряжений.
Правила Кирхгофа, записанные для узлов либо контуров цепи, дают полную систему линейных уравнений, которая позволяет отыскать все токи и все напряжения.
Перед тем, как составить уравнения, необходимо произвольно избрать:
положительные направления токов в ветвях и обозначить их на схеме, при всем этом не непременно смотреть, дабы в узле направления токов были и втекающими, и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в неприятном случае — отрицательным.
При записи линейно независящих уравнений по второму правилу Кирхгофа стремятся, дабы в каждый новый контур, для которого составляют уравнение, заходила хотя бы одна новенькая ветвь, не вошедшая в прошлые контуры, для которых уже записаны уравнения по второму закону (достаточное, но не нужное условие).
В сложных непланарных графах электрических цепей человеку тяжело узреть независящие контуры и узлы, каждый независящий контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение в определяющей задачку системе линейных уравнений. Подсчёт количества независящих контуров и их очевидное указание в определенном графе развит в теории графов.
На этом рисунке для каждой ветки обозначен протекающий по ней ток (буковкой «I») и напряжение между соединяемыми ею узлами (буковкой «U»)
Количество узлов: 3. Количество веток (в замкнутых контурах): 4. Количество веток, содержащих источник тока: 0. Количество контуров: 2. Для приведённой на рисунке цепи, в согласовании с первым правилом, производятся следующие соотношения:
Направьте внимание, что для каждого узла должно быть выбрано положительное направление, к примеру, тут токи, втекающие в узел, числятся положительными, а вытекающие — отрицательными.
Решение приобретенной линейной системы алгебраических уравнений позволяет найти все токи узлов и веток, таковой подход к анализу цепи принято именовать способом контурных токов.
В согласовании со вторым правилом, справедливы соотношения:
Приобретенные системы уравнений вполне обрисовывают анализируемую цепь, и их решения определяют все токи и все напряжения веток, таковой подход к анализу цепи принято именовать способом узловых потенциалов.
Законы кирхгофа
1-ый закон Кирхгофа — это закон баланса токов в разветвленной цепи, формулируется для узлов электрической цепи.
Он говорит: алгебраическая сумма токов в любом узле электрической цепи в хоть какой момент времени равна нулю, т.е.
где т — число веток, сходящихся в узле.
Знаки токов берутся с учетом заблаговременно избранных условных положительных направлений токов: все токи, направленные к узлу, берутся с одним знаком, а направленные от узла, — с обратным знаком.
Так для узла 1 схемы, изображенной на рис. 2.4, имеем:
I1 — I2 — I3 +J = 0.
1-ый закон Кирхгофа отражает базовый принцип электротехники — принцип непрерывности полного тока, учитывающий тот факт, что в узле не может быть скопления электрического заряда и не может быть его расхода; сумма зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла в один и тот же промежуток времени.
Число независящих уравнений, записанных по первому закону Кирхгофа равно числу независящих узлов и на одно уравнение меньше числа всех узлов, т.e.
N1 = q-1, (2.9)
где q — число всех узлов.
2-ой закон Кирхгофа — это закон баланса напряжений на замкнутых участках цепи, формулируется для контуров электрической цепи.
Он говорит: алгебраическая сумма напряжений в любом замкнутом контуре в хоть какой момент времени равна нулю:
где п — число частей, входящих в контур.
2-ая формулировка второго закона Кирхгофа: алгебраическая сумма ЭДС в любом замкнутом контуре цепи в хоть какой момент времени равна алгебраической сумме падений напряжений на элементах этого контура:
где т — число источников ЭДС, а п — число пассивных частей, включенных в контур.
В уравнениях (2.10) и (2.11) напряжения на элементах контура и ЭДС записывают со знаком плюс, если выбранное направление обхода контура (к примеру, по ходу часовой стрелки, рис. 1.25) совпадает с направлением напряжений (токов) на этих элементах. При всем этом направление обхода и направления токов в ветвях могут быть выбраны произвольно.
Пример1. Составим уравнение по второму закону Кирхгофа для цепи, изображенной на рис. 2.5.

Число независящих уравнений, записанных по второму закону Кирхгофа, равно числу независящих контуров:
N2 = p — (q — 1), (2.12)
где р — число веток с независящими токами (без веток с источниками тока);
q — число всех узлов.
Пример 2. Разглядим цепь, состоящую из последовательного соединенных резистора, конденсатора и катушки (рис. 2.6). На этот двухполюсник повлияет ЭДС e(t).
Так как через все элементы протекает один и тот же ток, то можно записать:
где оператор имеет смысл сопротивления и охарактеризовывает цепь, где действует возмущение e(t), т.е. оператор Z отражает собственные характеристики цепи.
Совокупа топологических и компонентных уравнений, решение которых позволяет найти неведомые токи и напряжения веток электрической цепи, именуется уравнениями электрического равновесия.
Как было показано ранее, уравнения (2.10) и (2.11) являются алгебраическими, а компонентные уравнения идеализированных частей могут быть как алгебраическими (2.1), так и дифференциальными (2.2), (2.3).
Поэтому, уравнения электрического равновесия цепи, составленные хоть каким способом, представляют собой в общем случае систему интегро-дифференциальных уравнений.
Законы Кирхгофа для магнитных цепей
При расчетах магнитных цепей, как и электрических, применяют 1-ый и 2-ой законы (правила) Кирхгофа.
1-ый закон Кирхгофа: алгебраическая сумма магнитных потоков в любом узле магнитной цепи равна нулю:

1-ый закон Кирхгофа для магнитных цепей следует из принципа непрерывности магнитного потока, известного из курса физики (см. также том 2 учебника).
2-ой закон Кирхгофа: алгебраическая сумма падений магнитного напряжения вдоль любого замкнутого контура равна алгебраической сумме МДС вдоль такого же контура:

2-ой закон Кирхгофа для магнитных цепей, на самом деле дела, есть другая форма записи закона полного тока.
Перед тем как записать уравнения по законам Кирхгофа, следует произвольно избрать положительные направления потоков в ветвях и положительные направления обхода контуров.
Если направление магнитного потока на некотором участке совпадает с направлением обхода, то падение магнитного напряжения этого участка заходит в сумму ?[/м со знаком «плюс», если встречно ему, то со знаком «минус».
Аналогично если МДС совпадает с направлением обхода, она заходит в Y, I w со знаком «плюс», в неприятном случае — со знаком «минус».
В качестве примера составим уравнения по законам Кирхгофа для разветвленной магнитной цепи, изображенной на рис. 14.12.
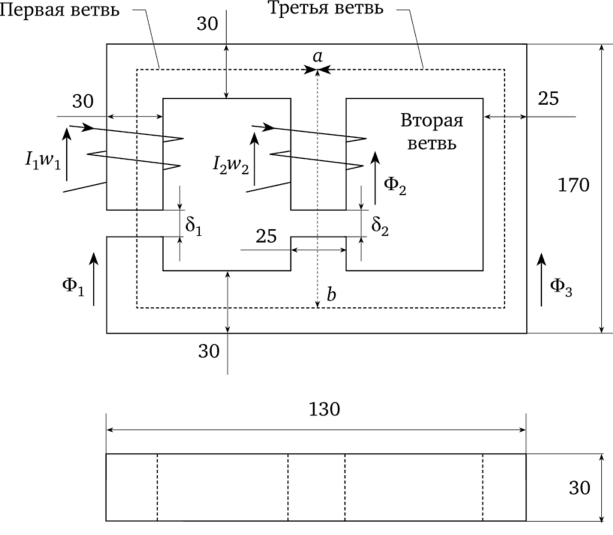
Левую ветвь назовем первой, и все относящиеся к ней величины запишем с индексом 1 (поток Ф1? напряженность поля Нь длина пути в стали 1Ь длина зазора МДС Среднюю ветвь назовем 2-ой, и все относящиеся к ней величины будут соответственно с индексом 2 (поток Ф2, напряженность поля Н2, длина пути в стали 12, длина зазора 82, МДС l2w2).
Все величины, относящиеся к правой ветки, имеют индекс 3 (поток Ф3, длина пути на вертикальном участке 12, суммарная длина пути на 2-ух горизонтальных участках 12).
Произвольно выберем направление потоков в ветвях. Положим, что все потоки (Ф3 Ф2, Ф3) ориентированы ввысь (к узлу а). Число уравнений, которые следует составить по законам Кирхгофа, должно быть равно числу веток цепи (в рассматриваемом случае необходимо составить три уравнения).
По первому закону Кирхгофа нужно составить столько уравнений, сколько в цепи узлов без единицы (см. параграф 2.8).
В цепи (рис. 14.12) два узла; поэтому, по первому закону Кирхгофа составим одно уравнение:

По второму закону Кирхгофа следует составить число уравнений, равное числу веток, за вычетом числа уравнений, составленных по первому закону Кирхгофа. В рассматриваемом примере по второму закону Кирхгофа составим 3-1 = 2 уравнения.
1-ое из этих уравнений составим для контура, образованного первой и 2-ой ветвями, 2-ое — для контура, образованного первой и третьей ветвями (для периферийного контура).
Перед составлением уравнений по второму закону Кирхгофа нужно избрать положительное направление обхода контуров. Будем обходить контуры по часовой стрелке.
Уравнение для контура, образованного первой и 2-ой ветвями, имеет вид
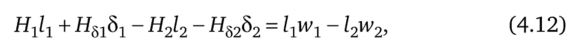
где Я51 и Я52 — напряженности поля соответственно в воздушных зазорах 5: и б2.
В левую часть уравнения вошли слагаемые Нг1> и Яб]81 со знаком «плюс», так как на первом участке поток Фх ориентирован согласно с обходом контура, слагаемые Н212 и Я5282 — со знаком «минус», так как поток Ф2 ориентирован встречно обходу контура.
В правую часть уравнения МДС l1w1 вошла со знаком «плюс», так как она ориентирована согласно с обходом контура, а МДС l2w2 — со знаком «минус», так как она ориентирована встречно обходу контура.
Составим уравнение для периферийного контура, образованного первой и третьей ветвями:
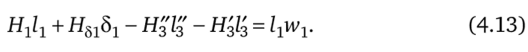
Вместе решать уравнения (4.11)—(4.13) с 3-мя неведомыми (Ф], Ф2, Ф3) не будем, так как в параграфе 14.8 дается решение рассматриваемой задачи более совершенным способом, чем способ на базе законов Кирхгофа, — способом 2-ух узлов.