При свертке параллельных веток эквивалентное сопротивление всегда меньше меньшего из сворачиваемых.
Если параллельно соединены n одинаковых сопротивлений (Рис. 3.3), эквивалентное сопротивление в n раз меньше сопротивления хоть какой из веток.
Если на участке цепи параллельно соединены только два элемента (Рис. 3.4), выражение (3.2) упрощается. В данном случае эквивалентное сопротивление можно найти как отношение произведения 2-ух сопротивлений к их сумме:
4. Главные ЗАКОНЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
К главным законам электрических цепей относятся закон Ома и законы Кирхгофа.
Закон Ома
Если в ветки не содержится ЭДС, к ней применим уже узнаваемый закон Ома для пассивного участка цепи (1.1). Его можно сконструировать и следующим образом. Ток в ветки, не содержащей ЭДС, равен падению напряжения в ветки, деленному на сопротивление ветки (Рис. 4.1):
Закон Ома для ветки, содержащей ЭДС, позволяет отыскать ток этой ветки по известной разности потенциалов на концах ветки. Ток в ветки, содержащей ЭДС, равен дроби, знаменатель которой – это сопротивление ветки. В числителе дроби – напряжение на концах ветки плюс алгебраическая сумма ЭДС, заключенных между концами ветки. С плюсом берутся напряжения и ЭДС, направление которых совпадает с направлением тока, с минусом – обратные.
А именно, ток в ветки, изображенной на Рис. 4.2, равен:
1-ый закон Кирхгофа
В любом узле цепи алгебраическая сумма токов равна нулю. При всем этом, токи, направленные к узлу, принято считать положительными, токи, направленные от узла, принято считать отрицательными (Рис. 4.3).
По первому закону Кирхгофа можно написать столько уравнений, сколько узлов содержит схема. Но не они все будут независящими. Если схема содержит узлов, независящими будут уравнений. Оставшееся уравнение будет являться следствием всех прошлых.
2-ой закон Кирхгофа
В любом замкнутом контуре цепи алгебраическая сумма напряжений равна алгебраической сумме ЭДС, включенных в контур.
При всем этом, положительными числятся те напряжения и ЭДС, которые совпадают с направлением обхода контура, отрицательными числятся напряжения и ЭДС, которые обратны направлению обхода контура. Направление обхода контура можно выбирать произвольно.
Метод составления уравнения по второму закону Кирхгофа для замкнутого контура цепи
Для данного контура (Рис. 4.4 а) уравнение по второму закону Кирхгофа составляется в следующем порядке:
- Задается направление токов в ветвях (Рис. 4.4 б).
- Выбирается направление обхода контура (Рис. 4.4 в).
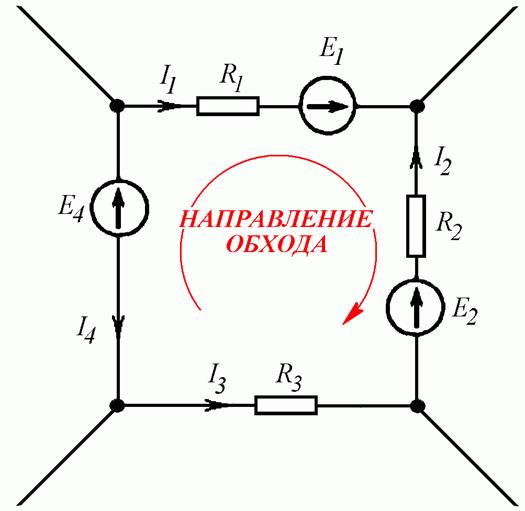
- Записывается уравнение, в левой части которого – сумма падений напряжений на сопротивлениях веток. В правой части – сумма ЭДС контура.
Примечание: Падение напряжения на сопротивлении ветки записывается в согласовании с известным уже законом Ома (1.1):
Использование второго закона Кирхгофа для незамкнутого участка цепи
2-ой закон Кирхгофа справедлив только для замкнутого контура. При всем этом, хоть какой незамкнутый участок цепи можно дополнить до замкнутого контура при помощи напряжения в разрыве незамкнутого участка.
Незамкнутый участок цепи abcd изображен на Рис. 4.5 а.
Дополняем участок до замкнутого контура, добавляя напряжение между незамкнутыми точками c и d (Рис. 4.5 б). Сейчас для контура abcd можно записать 2-ой закон Корхгофа:
Использование законов Кирхгофа при наличии в цепи источника тока
Источник тока имеет нескончаемо огромное сопротивление, потому не образует замкнутого контура и не может заходить в уравнения второго закона Кирхгофа. Но, в уравнениях первого закона Кирхгофа источник тока должен содержаться непременно.
По мере надобности записать уравнение по второму закону Кирхгофа для контура, содержащего источник тока, его подменяют напряжением на выводах источника тока.
Написать уравнение по первому закону Кирхгофа для узла a и уравнение по второму закону Кирхгофа для контура abcd (Рис. 4.6 а).
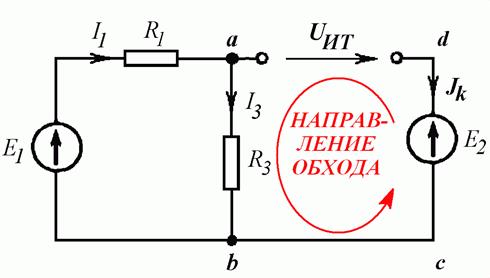
Уравнение по первому закону Кирхгофа для узла a содержит источник тока и имеет вид:
Для того дабы написать уравнение по второму закону Кирхгофа для контура abcd, заменяем источник тока напряжением на его выводах (Рис. 4.6 б), задаем направление обхода контура против часовой стрелки и получаем:
Для упрощения расчетов источник тока с параллельным сопротивлением можно поменять на эквивалентный источник ЭДС (Рис. 4.7). После расчета нужно непременно возвратиться к начальной схеме.
Независящий контур цепи
В принципе, по второму закону Кирхгофа можно составить столько уравнений, сколько контуров содержит цепь. Но не все эти уравнения будут независящими. Для определения независимости уравнений по второму закону Кирхгофа вводится такое понятие как независящий контур цепи.
Независящий контур цепи – это таковой контур, который содержит хотя бы одну новейшую ветвь, не вошедшую в другие контуры цепи.
Независящие контуры в общем случае выбираются произвольно, но проще всего выбирать их так, дабы они совпадали с ячейками цепи (Рис. 4.8 б).
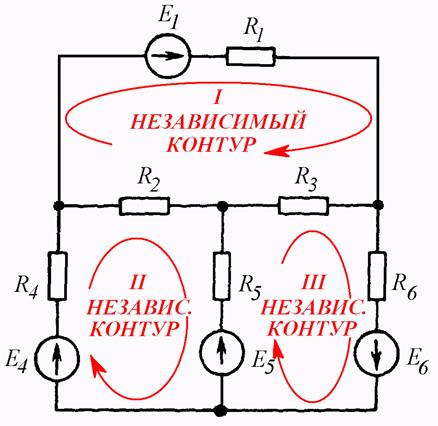
Если схема содержит веток и узлов, число независящих контуров равно
Схема на Рис. 4.8 б содержит три независящих контура.
5. СИСТЕМА УРАВНЕНИЙ ПО ЗАКОНАМ КИРХГОФА ДЛЯ РАСЧЕТА ТОКОВ ЦЕПИ
Законы Кирхгофа можно применять для расчета токов в ветвях цепи. Главное требование при всем этом – получение системы независящих уравнений, в какой число неведомых равно количеству токов, подлежащих определению.
1-ый и 2-ой законы Кирхгофа
Некоторые электрические цепи можно изобразить в виде обычного контура, содержащего источник питания и маленькое количество деталей — резисторов, конденсаторов либо других. Но есть и огромные схемы, включающие в себя несколько замкнутых веток. В этих случаях принципиально точно высчитать электрические характеристики на любом рассматриваемом участке. Законы Кирхгофа позволяют их найти путём составления и решения нескольких обычных уравнений.

1-ый закон Кирхгофа
Закон Ома обрисовывает связь между напряжением, сопротивлением и силой тока в обычных одноконтурных цепях. На практике почаще встречаются сложные разветвленные цепи, состоящие из нескольких контуров и многих узлов, которые нереально обрисовать, применяя стандартные правила для расчета последовательных и параллельных цепей.
Найти напряжение и силу тока в разветвленных цепях позволяют правила Кирхгофа, которые в технической литературе обычно именуют законами Кирхгофа. Хотя более корректным следует считать название «правила», так как они не являются базовыми законами природы. К примеру, 1-ое правило Кирхгофа вытекает из закона сохранения заряда. Оно говорит, что сумма всех токов в каждом узле электроцепи равна нулю.
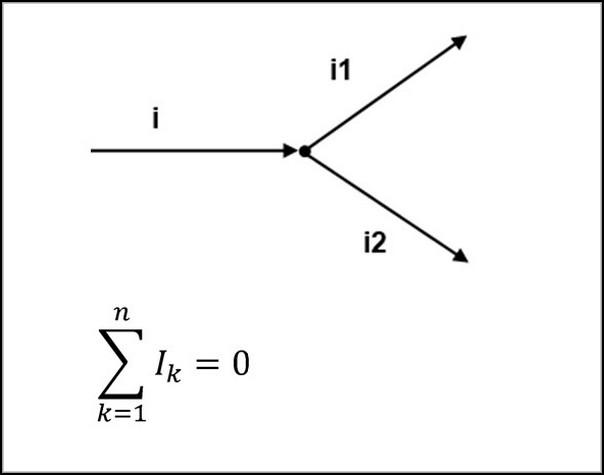
Формулировка закона просит уточнения следующих определений:
- Узел — это определённое место на схеме, в каком сходится 3 либо большее количество проводов. Узлами можно именовать точки, находящиеся в протяжении 1 провода, если в этих местах подсоединены ещё провода.
- Движение тока, направленного к определённому узлу, условно именуют положительным, обратное — отрицательным.
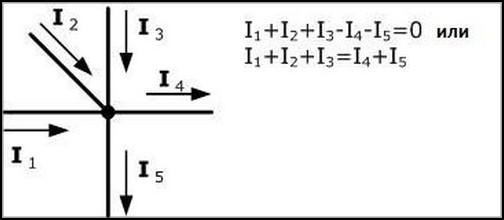
Закон Кирхгофа, если гласить ординарными словами, может быть сформулирован так: сколько токов втекает в узел, столько же и вытекает. Это свидетельствует о непрерывности тока для электрической цепи. Потому существует ещё одна формула, выражающая 1-ое правило Кирхгофа:
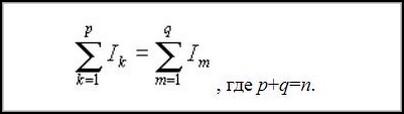
Тут с одной стороны знака равенства рассматриваются токи, входящие в определённый узел, а с другой — выходящие.
При использовании первого закона Кирхгофа для цепи переменного тока используются секундные значения напряжений, которые принято обозначать буковкой İ. Расчеты в данном случае проводятся по уравнению, представленному в всеохватывающей форме.
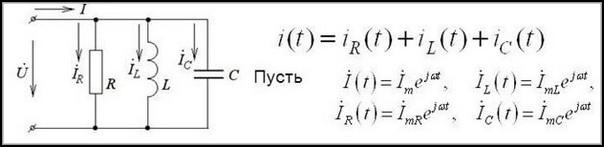
2-ой закон Кирхгофа
Когда рассматривается электрическая цепь, подключённая к источнику тока, в каждой её точке имеется определённый потенциал. Разность между ними создаёт электрическое поле, которое вызывает перемещение зарядов.
Цепь представляет собой замкнутый контур, по которому движутся электроны. Электрическое поле делает определённую работу по их перемещению. Каждый заряд перемещается по цепи, а потом под действием ЭДС источника замыкает круг.
2-ой закон Кирхгофа говорит, что работа по перемещению заряда вдоль любого контура электроцепи с возвратом в исходную точку равна нулю. В этой формулировке предполагается хоть какой замкнутый контур, при этом как тот, который включает источник питания, так и о тот, где его нет.
Работа электрического поля при перемещении заряда в рассматриваемом случае представляет собой сумму падений напряжения для каждого из участков контура. Таким макаром, 2-ое правило либо закон Кирхгофа говорит, что сумма напряжений всех веток в контуре приравнивается нулю. Это можно выразить в виде следующего уравнения:
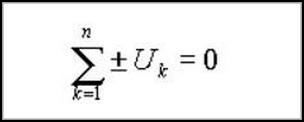
Если напряжение и направление обхода контура совпадают, то U записывают со знаком плюс, в неприятном случае — со знаком минус. Направление обхода избранного контура может быть определено произвольным образом. 2-ое правило Густава Кирхгофа его не регламентирует.
Если в контуре есть один либо несколько источников питания, то формулу можно выразить следующим образом:
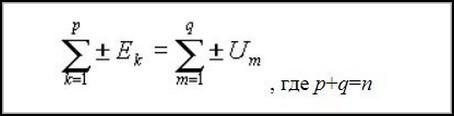
Тут имеется p источников питания, q участков контура. Сумма всех ЭДС имеющихся источников питания равна сумме падений напряжения.
Значение правил Кирхгофа
Законы Кирхгофа выражают фундаментальные принципы физики. Их формулировки кажутся очень ординарными и явными. Но по сути они представляют собой способ, позволяющий высчитать электрические характеристики сетей очень сложной конфигурации.
При помощи законов Кирхгофа можно составить систему независящих уравнений для расчета характеристик электрической цепи. Принципиально, дабы их количество было не меньше, чем число характеристик, которые нужно найти.
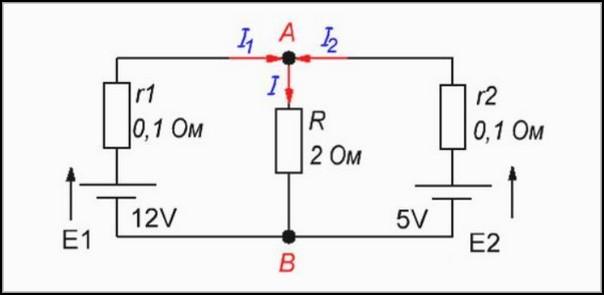
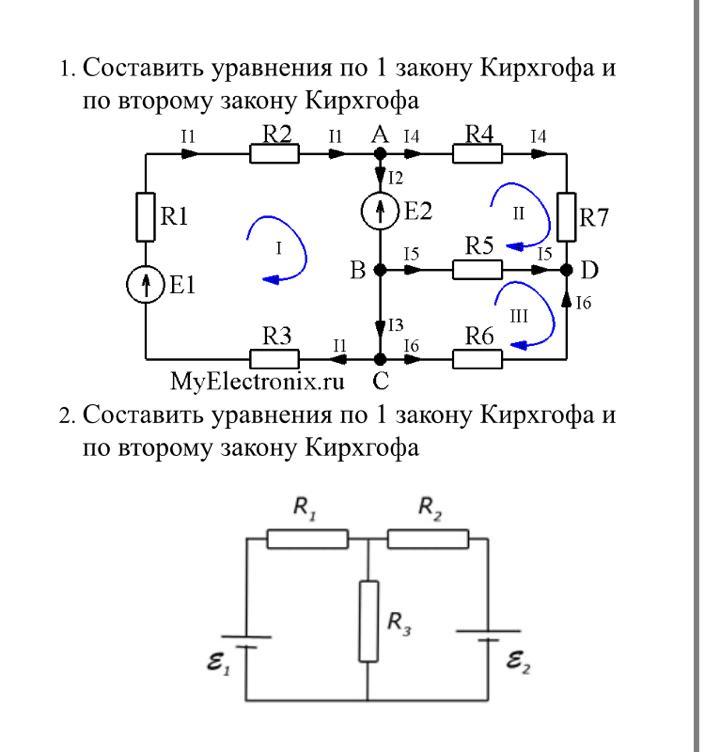
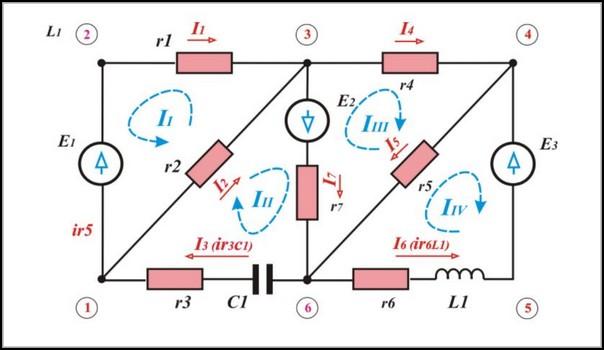
На приведённом рисунке представлена электроцепь, для которой будет проводиться расчёт. Используя 1-ый закон либо правило Кирхгофа, для узла A можно записать:
В этот узел входят два тока, а выходит один. Дальше нужно применить 2-ое правило. Для этого можно избрать наружный контур. Видно, что тут имеется два источника тока и два резистора. Потому будут получены уравнения:

Тут приведены 2 эквивалентные формулы. В левой части равенства учтены электродвижущие силы 2-ух источников тока, в правой — падение напряжения на обоих резисторах с учётом направления токов. Ещё одно уравнение можно получить из 2 закона при обходе по правому внутреннему контуру:

В итоге получена система, включающая в себя три уравнения с 3-мя неведомыми:

Используя определенные данные, можно подставить в систему уравнений численные значения и отыскать, чему равна сила тока для каждой ветки, относящейся к узлу A. При расчётах принципиально осознавать, что при довольно сложной конфигурации электроцепи время от времени бывает тяжело найти направление силы тока для каждой ветки.
1-ый и 2-ой законы Густава Кирхгофа позволяют точно найти не только лишь величину тока, но и его символ. Если в приведённом примере после вычисления разыскиваемых значений при помощи представленной системы уравнений окажется, что ток с индексом 2 воспринимает отрицательное значение, то это значит, что по сути он имеет направление, обратное обозначенному на рисунке.
Законы для магнитного поля
Правила Кирхгофа отыскали свое использование и при расчете магнитных цепей. 1-ый закон Кирхгофа для магнитной цепи смотрится так:
Проще говоря, сумма всех магнитных потоков, проходящих через узел, приравнивается нулю.
2-ой закон в применении к магнитным полям звучит следующим образом: «Сумма магнитодвижущих сил в контуре приравнивается сумме магнитных напряжений». Формула смотрится так:

Кирхгофом выведены правила, имеющие абсолютный прикладной нрав. С помощью их можно решать практические вопросы в электротехнике. Обширное использование этих правил разъясняется простотой формулировки уравнений и возможностью их решения с применением стандартных методов линейной алгебры.
Расчет электрической цепи по закону Кирхгофа

Закон Ома устанавливает зависимость между силой тока, напряжением и сопротивлением для простейшей электрической цепи, представляющей собой один замкнутый контур. В практике встречаются более сложные (разветвленные) электрические цепи, в каких имеются несколько замкнутых контуров и несколько узлов, к которым сходятся токи, проходящие по отдельным веткам. Значения токов и напряжений для таких цепей можно отыскивать с помощью законов Кирхгофа.

Законы Кирхгофа для магнитной цепи
Магнитная цепь (МЦ), как электрическая (ЭЦ), может быть рассчитана по данным правилам. По аналогии цепей можно выделить следующую связь:
- магнитный поток – электрический ток;
- МДС (магнитодвижущая сила) – ЭДС.
Читайте также: Создатель трансформатора переменного тока
1-ое правило для МЦ – магнитные потоки в узлах в алгебраической сумме дают ноль (ΣΦк= 0). Оно основано на физическом принципе непрерывности Φ.
2-ое правило гласит о том, что падения магнитного напряжения (напряжённости) Uм в сомкнутом контуре в алгебраической сумме равны сумме МДС этого контура:
ΣUм = ΣI*ω, где:
- I – ток, проходящий по проводнику;
- ω – количество витков в обмотке.
2-ой закон Кирхгофа – это по-другому записанная форма закона полного тока.
Внимание! Для магнитных цепей метод составления уравнений тот же самый, как и для ЭЦ. Правила символов действуют аналогично.
1-ый закон
1-ый закон Кирхгофа устанавливает зависимость между токами для узлов электрической цепи, к которым подходит несколько веток. Согласно этому закону алгебраическая сумма токов веток, сходящихся в узле электрической цепи, равна нулю:
При всем этом токи, направленные к узлу, берут с одним знаком (к примеру, положительным), а токи, направленные от узла,— с обратным знаком (отрицательным). К примеру, для узла А
I1 + I2 + I3 – I4 – I5 = 0 (17)
Это любопытно! Все о полупроводниковых диодиках.
Преобразуя это уравнение, получим, что сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла:
I1 + I2 + I3 = I4 + I5 (17′)
В этом случае имеет место полная аналогия с рассредотачиванием потоков воды в соединенных вместе трубопроводах.
Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях случайного типа. Законы Кирхгофа имеют особенное значение в электротехнике из-за собственной универсальности, так как применимы для решения всех электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при неизменных и переменных напряжениях и токах.
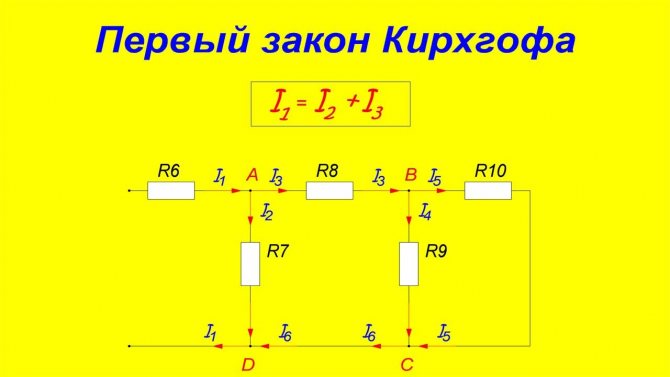
1-ый закон Кирхгофа.
Читайте также: Электромагнитная индукция. Правило Ленца
2-ой закон Кирхгофа устанавливает зависимость между э. д. с. и напряжением в замкнутой электрической цепи. Согласно этому закону во всяком замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжения на сопротивлениях, входящих в этот контур:
При составлении формул, характеризующих 2-ой закон Кирхгофа, значения э. д. с. E и падений напряжений IR считают положительными, если направления э. д. с. и токов на соответственных участках контура совпадают с произвольно избранным направлением обхода контура. Если же направления э. д. с. и токов на соответственных участках контура обратны избранному направлению обхода, то такие э. д. с. и падения напряжения считают отрицательными.
Разглядим в качестве примера электрическую цепь, в какой имеются два источника с электродвижущими силами E1 и E2, внутренними сопротивлениями Ro1, Ro2 и два приемника с сопротивлениями R1 и R2. Применяя 2-ой закон Кирхгофа для «этой цепи и выбирая направление ее обхода по часовой стрелке,
Будет интересно
E1 – E2 = IR01 + IR02 + IR1 + IR.
При всем этом э. д. с. E1 и ток I совпадают с избранным направлением обхода контура и числятся положительными, а э. д. с. Е2, обратная этому направлению, считается отрицательной. Если в электрической цепи э. д. с. источников электроэнергии при обходе соответственного контура ориентированы навстречу друг дружке (см. рис. 24, а), то такое включение именуют встречным. В данном случае на основании второго закона Кирхгофа ток I = (E1-E2)/(R1+R2+R01+R02).
Встречное направление э. д. с. имеет место, к примеру, на э. п. с.при включении электродвигателей неизменного тока (их можно рассматривать как некоторые источники э. д. с.) в две параллельные группы, также при параллельном включении аккумов в батарее.
Если же э. д. с. источников электроэнергии имеют по контуру однообразное направление (рис. 24, б), то такое включение именуют согласным и ток I = (E1-E2)/(R1+R2+R01+R02). В некоторых случаях такое включение неприемлимо, так как ток в цепи резко растет.
Если в электрической цепи имеются ответвления (рис. 24, в), то по отдельным ее участкам проходят разные токи I1 и I2. Согласно второму закону Кирхгофа E1-E2=I1R01+I1R1-I2R2-I2R02-I2R3+I1R4.
При составлении этого уравнения э. д. с. Е1 и ток I1 числятся положительными, так как совпадают с принятым направлением обхода контура, э. д. с. Е2 и ток I2 — отрицательными.
2-ой закон Кирхгофа — практическое использование
На практике 2-ой закон Кирхгофа применяется удачно для расчета электрических цепей. Благодаря его объяснению можно высчитать нужные характеристики в сложных электрических цепях. Когда находится необходимость высчитать значение тока и/либо направление всегда выручит 2-ой закон Кирхгофа. Несмотря на то, что правила Кирхгофа были сформулированы в дальнем 1845 году, они проявили себя как рабочие и не вызывают вопросы ни у кого. Теория электрических цепей была бы неполной без наличия этих законов, которые так отлично подходят для решения разных уравнений в этой области.
Если материал был полезен, вы сможете
выслать донат либо поделиться данным материалом в соц сетях:
2-ой закон
Для расчетов сложных электрических цепей с несколькими источниками энергии применяют 2-ой закон Кирхгофа, который может быть сформулирован так: во всяком замкнутом электрическом контуре алгебраическая сумма всех э. д. с. равна алгебраической сумме падений напряжения в сопротивлениях, включенных последовательно в эту цепь, т. е.
Читайте также: Устройство полупроводникового диодика, p-n переход.
E1 + E2 + E3 + . . . = I1r1 + I2r2 + I3r3 + . . .
Будет интересно
При всем этом положительными следует считать э. д. с. и токи, направление которых совпадает с направлением обхода контура. Если в электрическую цепь включены два источника энергии, э. д. с. которых совпадает по направлению (рис. 20, а), то э. д. с. всей цепи равна сумме э. д. с. этих источников, т. е. E = E1 + E2. Если же в цепи э. д. с. источников имеют обратные направления, то результирующая э. д. с. равна разности э. д. с. этих источников, т. е.
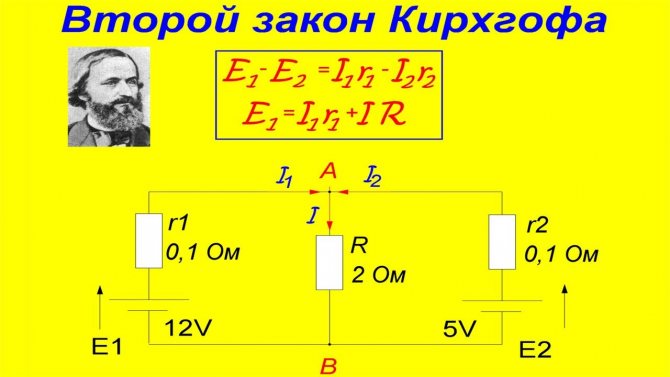
2-ой закон Кирхгофа.
При последовательном включении в электрическую цепь нескольких источников энергии с разным направлением э. д. с. общая э. д. с. равна алгебраической сумме э. д. с. всех источников. При суммировании э. д. с. 1-го направления берут со знаком плюс, а э. д. с. обратного направления — со знаком минус. При составлении уравнений выбирают направление обхода цепи и произвольно задаются направлениями токов.
Замкнутая цепь обозначена знаками а, б, в и г. Ввиду наличия ответвлений в точках а, б, в, г токи I1, I2, I3 и I4, отличаясь по силе, могут иметь разные направления. Для таковой цепи в согласовании со вторым законом Кирхгофа можно написать:
E1 – E2 – E3 = I1(r01 + r1) – I2(r02 + r2) – I3(r03 + r3) + I4r4,
где r01, r02, r03 — внутренние сопротивления источников энергии, r1, r2, r3, r4 — сопротивления приемников энергии. В личном случае при отсутствии ответвлений и последовательном соединении проводников общее сопротивление равно сумме всех сопротивлений. Если наружняя цепь источника энергии с внутренним сопротивлением r состоит, к примеру, из 3-х последовательно соединенных проводников с сопротивлениями, соответственно равными r1, r2, r3, то на основании второго закона Кирхгофа можно написать следующее равенство:
E = I r + I r1 + I r2 + I r3.
При нескольких источниках тока в левой части этого равенства была бы алгебраическая сумма э. д. с. этих источников.
2-ой закон Кирхгофа и его определение
В едином замкнутом контуре алгебраическая сумма ЭДС будет приравниваться на значение, которое суммирует конфигурации напряжения на всеобщее количество резистивных частей данного контура.
2-ое правило Кирхгофа животрепещуще в сетях с неизменным и/либо переменным током. В формулировке закона применяется конкретно понятие алгебраическая сумма, так как она может быть указана со знаком плюс либо минус. Четкое определение может быть в таком случае только средством обычного, но действенного метода. Для начала нужно подобрать какое-то направление для обхода контура, по/против часовой стрелке, на собственное усмотрение. Само направление тока подбирается только через элементы цепи. После следует найти знаки «+» и «-» для напряжениях и ЭДС. Напряжения необходимо записывать с отрицательным знаком, когда ток не соответствует обходу контура в плане направления и с плюсом в случае совпадения. То же самое правило необходимо применять и в этом случае, когда стоит отметить ЭДС.
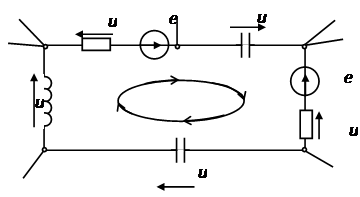
Закон кирхгофа расчет цепи
Способ ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА
Способ эквивалентного генератора правильно использовать в этом случае, когда нужна найти ток (либо отыскать его аналитическое выражение) только в одной ветки цепи, без нахождения токов в других ветвях.
В базе способа лежит замена части цепи, присоединенной к зажимам данной ветки, эквивалентным источником и определение характеристик этого источника. Зависимо от выбора вида эквивалентного источника различают способ эквивалентного генератора напряжения (источник ЭДС) либо эквивалентного генератора тока (источник тока).
Расчёт способом эквивалентного генератора напряжения заключается в определении ЭДС и внутреннего сопротивления эквивалентного источника и состоит в следующем.
Что такое правило напряжений Кирхгофа (2-ой закон Кирхгофа)?
Принцип, узнаваемый обычно напряжений Кирхгофа (открытое в 1847 году германским физиком Густавом Р. Кирхгофом), можно сконструировать следующим образом:
«Алгебраическая сумма всех напряжений в замкнутом контуре равна нулю»
Под алгебраической я подразумеваю, кроме учета величин, учет и символов (полярностей). Под контуром я подразумеваю хоть какой путь, прослеживаемый от одной точки в цепи до других точек в этой цепи, и, в конце концов, назад в начальную точку.
Закон кирхгофа расчет цепи онлайн
Другими словами сколько току вытекло в качестве тока I3 в точке А, столько его и возвратилось к нам в точке B в виде тока I4. Высшая справедливость всё-таки восторжествовала. А посодействовало нам при всем этом здравое рассуждение, о том, что в хоть какой точке цепи, где электрическая сеть разветвляется, полное количество тока, вытекающего из узла, другими словами этой точки, равно количеству тока, втекающего в этот узел. Потому смело рисуем схему, зная, что нам посодействовал уже 1-ый, а не 2-ой закон Кирхгофа:
Почему-либо оказалось, что токи I3 и I4 оказались точно равными -I1, и значит… наши лампочки зажглись полным накалом.
Ох уж эти выдумки инопланетянские! С нашей стороны осталось исключительно в схеме поставить стрелочки токов (и ЭДС у источника ЭДС Eин) в обратное направление.