Закон Кирхгофа (правила Кирхгофа), сформулированные Густавом Кирхгофом в 1845 году, являются следствиями из базовых законов сохранения заряда и безвихревости электростатического поля.
Закон Кирхгофа – это соотношения, выполняемые между токами и напряжениями на участках всех электрических цепей. Они позволяют рассчитывать любые электрические цепи: неизменного, переменного либо квазистационарного тока.
При формулировании правил Кирхгофа применяют такие понятия, как ветвь, контур и узел электрической цепи.
- Ветвь – участок электрической цепи с одни и этим же током.
- Узел – точка соединения 3-х либо более веток.
- Контур – замкнутый путь, проходящий через несколько узлов и веток разветвлённой электрической цепи.
При обходе нужно учитывать, что ветвь и узел могут сразу принадлежать нескольким контурам. Правила Кирхгофа справедливы как для линейных, так и для нелинейных цепей при любом нраве конфигурации во времени токов и напряжений. Правила Кирхгофа обширно используются при решении задач электротехники за счет легкости в расчетах.
1 закон Кирхгофа
В цепях, состоящих из последовательно соединенных источника и приемника энергии, соотношения между током, сопротивлением и ЭДС всей цепи либо на каком-либо участке цепи определяются законом Ома. Но на практике в цепях токи от какой-нибудь точки идут по различным путям (Рис. 1). Потому становиться животрепещущим введение новых правил для проведения расчетов электрических цепей.
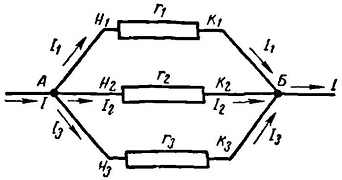
Рис. 1. Схема параллельного соединения проводников.
Так, при параллельном соединении проводников начала всех проводников соединены в одну точку, а концы проводников – в другую точку. Начало цепи присоединяется к одному полюсу источника напряжения, а конец цепи – к другому полюсу.
Из рисунка видно, что при параллельном соединении проводников для прохождения тока есть некоторое количество путей. Ток, протекая к точке разветвления А, разливается дальше по трем сопротивлениям и равен сумме токов, выходящих из этой точки: I = I1 + I2 + I3.
Согласно первому правилу Кирхгофа алгебраическая сумма токов веток, сходящихся в каждом узле хоть какой цепи равна нулю. При всем этом направленный к узлу ток принято считать положительным, а направленный от узла – отрицательным.
Запишем 1-ый закон Кирхгофа в всеохватывающей форме:
1-ый закон Кирхгофа говорит, что алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла. Другими словами, сколько тока втекает в узел, столько же вытекает (как следствие закона сохранения электрического заряда). Алгебраическая сумма — это сумма, в которую входят слагаемые со знаком плюс и со знаком минус.
Рис. 2. i_1+i_4=i_2+i_3.
Разглядим использование 1 закона Кирхгофа на следующем примере:
- I1 – это полный ток, текущий к узлу А, а I2 и I3 — токи, вытекающие из узла А.
- Тогда мы можем записать: I1 = I2 + I3.
- Аналогично для узла B: I3 = I4 + I5.
- Пусть, что I4 = 5 А и I5 = 1 А, получим: I3 = 5 + 1 = 6 (А).
- Пусть I2 = 10 А, получим: I1 = I2 + I3 = 10 + 6 = 16 (А).
- Запишем схожее соотношение для узла C: I6 = I4 + I5 = 5 + 1 = 6 А.
- А для узла D: I1 = I2 + I6 = 10 + 6 = 16 А
- Таким макаром мы наглядно лицезреем справедливость первого закона Кирхгофа.
2 закон Кирхгофа
При расчете электрических цепей почти всегда нам встречаются цепи, образующие замкнутые контуры. В состав таких контуров, не считая сопротивлений, могут заходить ЭДС (источники напряжений). На рисунке 4 представлен участок таковой электрической цепи. Произвольно избираем положительные направления токов. Обходим контур от точки А в случайном направлении (выберем по часовой стрелке). Разглядим участок АБ: происходит падение потенциала (ток идет от точки с высшим потенциалом к точке с низшим потенциалом).
- На участке АБ: φА + E1 – I1r1 = φБ.
- БВ: φБ – E2 – I2r2 = φВ.
- ВГ: φВ – I3r3 + E3 = φГ.
- ГА: φГ – I4r4 = φА.
- Складывая данные уравнения, получим: φА + E1 – I1r1 + φБ – E2 – I2r2 + φВ – I3r3 + E3 + φГ – I4r4 = φБ + φВ + φГ + φА
- либо: E1 – I1r1 – E2 – I2r2 – I3r3 + E3 – I4r4 = 0.
- Откуда имеем следующее: E1 – E2 + E3 = I1r1 + I2 r2 + I3r3 + I4r4.
Таким макаром, получаем формулу второго закона Кирхгофа в всеохватывающей форме:
Уравнение для неизменных напряжений — Уравнение для переменных напряжени —
Сейчас можем сконструировать определение 2 (второго) закона Кирхгофа:
2-ой закон Кирхгофа говорит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура, равна алгебраической сумме ЭДС, входящих в этот контур. В случае отсутствия источников ЭДС, суммарное напряжение равно нулю.
По другому формулируя 2-ое правило Кирхгофа, можно сказать: при полном обходе контура потенциал, изменяясь, ворачивается к исходному значению.
При составлении уравнения напряжений для контура необходимо избрать положительное направление обхода контура, при всем этом падение напряжения на ветки считается положительным, если направление обхода данной ветки совпадает с ранее избранным направлением тока ветки, в неприятном случае – отрицательным.
Найти символ можно по методу:
- 1. избираем направление обхода контура (по либо против часовой стрелки);
- 2. произвольно избираем направления токов через элементы цепи;
- 3. расставляем знаки для напряжений и ЭДС по правилам (ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура со знаком «+», по другому – «-»; напряжения, падающие на элементах цепи, если ток, протекающий через эти элементы совпадает по направлению с обходом контура, со знаком «+», в неприятном случае – «-»).
Закон Ома является личным случаем второго правила для цепи.
Приведем пример использования второго правила Кирхгофа:
По данной электрической цепи (Рис 6) нужно отыскать ее ток. Произвольно берем положительное направление тока. Выберем направление обхода по часовой стрелке, запишем уравнение 2 закона Кирхгофа:
Символ минус значит, что выбранное нами направление тока обратно его реальному направлению.
Решение задач
1. По приведенной схеме записать законы Кирхгофа для цепи.
-
Входные данные:
- R1
- R2
- R3
- E1
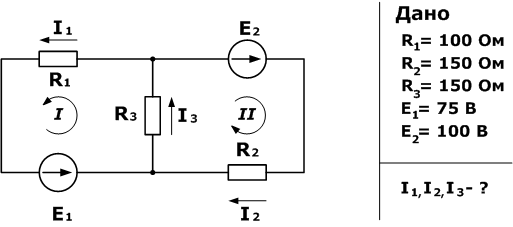
- E2
- I1 – ?
- I2 – ?
- I3 – ?
- Используя 1-ый закон Кирхгофа, запишем уравнение для цепи. Сумма токов сходящихся в узле равна нулю. Примем входящие токи положительными, а выходящие отрицательными. Тогда:
- Используя 2-ой закон Кирхгофа составим уравнения для первого и второго контуров цепи.
- Направления обхода произвольны, при всем этом если направление тока через резистор совпадает с направлением обхода, символ «+», если по другому, то «-». С источниками ЭДС так же.
- Для первого контура токи I1 и I3 совпадают с направлением обхода, ЭДС Е1 также совпадает, другими словами берем их со знаком «+».
- Для первого и второго контуров по второму закону Кирхгофа получаем следующие уравнения:
- Таким макаром, получаем систему из 3-х уравнений, являющуюся решением задачи:
2. На рисунке приведена цепь с 2-мя источниками ЭДС величиной 12 В и 5 В, с внутренним сопротивлением источников 0,1 Ом, работающих на общую нагрузку 2 ома. Как будут распределены токи в этой цепи, какие они имеют значения?.
Составление системы уравнений, нужных для определения токов по первому и второму законам Кирхгофа. Нахождение токов, используя способ контурных токов
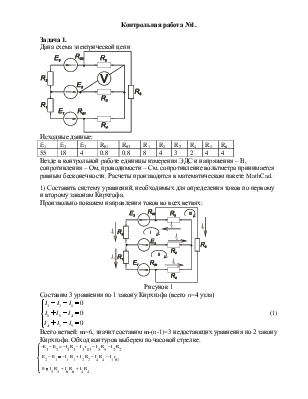
Всюду в контрольной работе единицы измерения ЭДС и напряжения – В, сопротивления – Ом, проводимости – См, сопротивление вольтметра принимается равным бесконечности. Расчеты выполняются в математическом пакете MathCad.
1) Составить систему уравнений, нужных для определения токов по первому и второму законам Кирхгофа.
Произвольно покажем направления токов во всех ветвях:
Составим 3 уравнения по 1 закону Кирхгофа (всего n=4 узла)
Всего веток: m=6, означает составим m-(n-1)=3 недостающих уравнения по 2 закону Кирхгофа. Обход контуров выберем по часовой стрелке.
При помощи (1) и (2) можно отыскать решения для всех токов цепи.
2) Отыскать все токи, пользуясь способом контурных токов.
Направление обхода контурных токов снутри имеющихся ячеек обозначено на рис.1.
Для каждого контура-ячейки составим уравнение по второму закону Кирхгофа
(Iк – контурные токи)
Решая данную систему, находим контурные токи:
Токи во внутренних ветвях схемы определяются как сумма либо разность соответственных контурных токов. Токи во наружных ветвях схемы равны контурным.
По знаку видно, что I6 должен быть ориентирован в другую сторону (в последующих расчетах I6>0)
3) За ранее упростив схему, заменив треугольник сопротивлений R4, R5, R6 эквивалентной схемой, начертить расчетную схему с эквивалентной звездой и показать на ней токи. Проверить корректность решения предшествующего пт, применив способ узлового напряжения.
Приобретенная схема с токами после преобразований показана на рис.2.
Применим способ узлового напряжения между узлами а и b:
где G1, G2, G3 – сопротивления соответственных веток:
Найдем токи в ветвях по закону Ома:
Приобретенные значения токов совпадают с токами, отысканными в п.2.
4) Найти ток в резисторе R6 способом эквивалентного генератора.
Определим напряжение холостого хода Ucd на резисторе R6, для этого воспользуемся формулой узлового напряжения для узлов а и b:
Воспользуемся законом Ома для определения личных напряжений:
Определим эквивалентное сопротивление Rэк cd. Схема в данном случае воспринимает вид, показанный на рис.4а. Для нахождения общего сопротивления, преобразуем треугольники acb в звезду (рис 4б), тогда:
Общее эквивалентное сопротивление цепи:
Ток I6 в резисторе R6 находится по формуле эквивалентного генератора:
Как лицезреем, данное значение тока совпадает со значением, отысканным в п.2, что свидетельствует о корректности решения.
5) Найти показания вольтметра и составить баланс мощностей для данной схемы.
Показания вольтметра можно найти по закону Ома:
Уравнение баланса отражает равенство мощностей, отдаваемой источником (Ри) и используемой приемниками (Рп), т.е.
Ри= Рп, поэтому баланс мощностей соблюдается, задачка решена правильно.
6) Выстроить в масштабе потенциальную диаграмму для наружного контура.
Возможной диаграммой именуется график рассредотачиваний потенциалов вдоль какого-нибудь контура. Потенциальную диаграмму строят как зависимость (потенциалов от сопротивления). Обозначения узлов см. на рис.5. За нулевой потенциал принимаем точку d. Найдем значения потенциалов других узлов (обход наружного контура по часовой стрелке):
Учет знака выбирался из правил: ток течет от большего потенциала к наименьшему, наращивание потенциала за счет ЭДС соответствует знаку источника, присоединенного к измеряемой точке.
Построим потенциальную диаграмму:
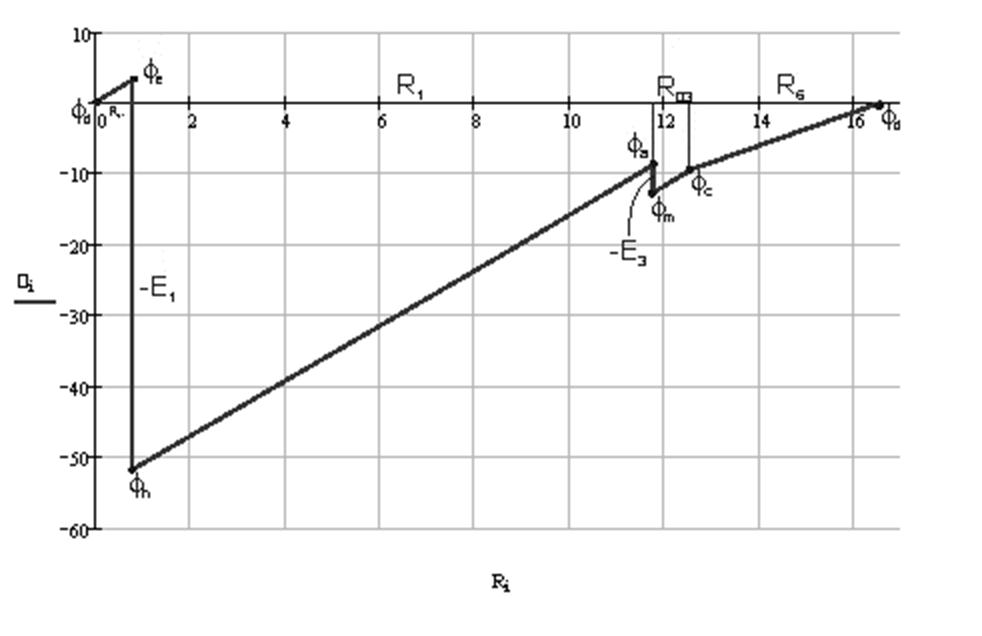
Диаграмма начинается и завершается с потенциалом , потенциалы посчитаны верно.
Дана электрическая схема.
Переведем начальные данные: 300мкФ=3·10 -4 Ф; 19.1мГн=1,91·10 -2 Гн; 15.9мГн=1,59·10 -2 Гн; 31.8мГн=3,18·10 -2 Гн
1) Найти токи во всех ветвях цепи и напряжения на отдельных участках. Найти показание вольтметра.
Определим всеохватывающие сопротивления веток:
где — угловая частота
Полное всеохватывающее сопротивление:
Исходная фаза ЭДС Е принимается равной нулю, потому всеохватывающая составляющая равна нулю:
Ток в неразветвленной части цепи:
Токи в параллельных цепях находятся по соотношениям:
=1,93-1,66j=2,54e -40°38′ j А
=0,77+1,01j=1,27e 52°54′ j А
Напряжения на отдельных участках:
=111,72-9,65j=112,14e -4°56′ j В
=8,28+9,65j=12,71e 49°21′ j В
Вольтметр будет демонстрировать действительную величину напряжения, которая находится по выражению:
2) Составить баланс активной и реактивной мощностей. Найти показание активной мощности, измеряемой ваттметром.
Полная мощность всей цепи:
=323,54-77,47j=332,69e -13°27′ j В·А
Действительная часть комплекса – активная мощность, надуманная часть – реактивная мощность.
Таким макаром, ваттметр будет демонстрировать мощность 323,5 Вт.
Найдем активные и реактивные мощности отдельных участков цепи.
Отысканная сумма активных мощностей отдельных участков равна активной мощности всей цепи.
С учетом погрешности вычислений, можно сказать, что отысканная сумма реактивных мощностей отдельных участков равна реактивной мощности всей цепи.
Таким макаром, баланс потребляемой и отдаваемой мощностей соблюдается.
3) Выстроить в масштабе на всеохватывающей плоскости векторную диаграмму токов и потенциальную диаграмму напряжений по наружному контуру.
Векторная диаграмма токов – изображение векторов отысканных токов, исходящих из одной точки. Поначалу откладываем токи I2 и I3, их геометрическая сумма дает ток I1. (Токи строились в масштабе 10:1)
Возможная диаграмма напряжений – направленные отрезки, соединяющие точки, надлежащие потенциалам каждой точки контура. Обычно обход контура берется против направления тока (в нашем случае, против часовой стрелки) – контур abcdef.
Определим длину отрезков, нужных отложить на диаграмме:
Отложение отрезков начинается из точки (0;0), Uab – падение напряжение на катушке, потому отрезок откладывается с опережением на 90° (перпендикулярно направлению I3 против часовой стрелки), потом от конца Uab откладывается отрезок Ubc (падение на конденсаторе) перпендикулярно I3 (против направления Uab). Ucd откладывается синфазно I3, Ude – синфазно I1, Uef – перпендикулярно I1. Точка конца диаграммы совпадает с отрезком общего напряжения Е, означает расчет произведен правильно.
Составление для схемы уравнений по законам Кирхгофа. Пример.
Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях случайного типа.
1-ый закон Кирхгофа вытекает из закона сохранения заряда. Он заключается в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.
Где n – число токов, сходящихся в данном узле. К примеру, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 — I2 + I3 — I4 + I5 = 0
В этом уравнении токи, направленные к узлу, приняты положительными.
2-ой закон Кирхгофа:алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре
где k – число источников ЭДС; m – число веток в замкнутом контуре; Ii, Ri – ток и сопротивление i-й ветки.
Так, для замкнутого контура схемы (рис. 2) Е1 — Е2 + Е3 = I1R1 — I2R2 + I3R3 — I4R4
Замечание о знаках приобретенного уравнения:
1) ЭДС положительна, если ее направление совпадает с направлением произвольно избранного обхода контура;
2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.
Составление для схемы уравнений по законам Кирхгофа. Пример.
Законы Кирхгофа применяют для нахождения токов в ветвях схемы. Обозначим число всех веток схемы в, число веток, содержащих источники тока, — вит и число узлов у. В каждой ветки схемы течет свой ток. Так как токи в ветвях с источниками тока известны, то число неведомых токов приравнивается в — вит. Перед тем как составить уравнения, нужно произвольно избрать: а) положительные направления токов в ветвях и обозначить их на схеме; б) положительные направления обхода контуров для составления уравнений по второму закону Кирхгофа.
Рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми, к примеру по часовой стрелке.
Дабы получить линейно независящие уравнения, по первому закону Кирхгофа составляют уравнения, число которых равно числу узлов без единицы, т. е. у — 1.
Уравнение для последнего у-го узла не составляют, так как оно совпало бы с уравнением, приобретенным при суммировании уже составленных уравнений для у — 1 узлов.
По второму закону Кирхгофа составляют уравнения, число которых равно числу веток без источников тока (в — вит), за вычетом уравнений, составленных по первому закону Кирхгофа, т. е. (в — вит) — (у — 1) = в — вит — у + 1.
Составляя уравнения по второму закону Кирхгофа, следует окутать все ветки схемы, исключая только ветки с источниками тока.
При записи линейно независящих уравнений по второму закону Кирхгофа стремятся, дабы в каждый новый контур, для которого составляют уравнение, заходила хотя бы одна новенькая ветвь, не вошедшая в прошлые контуры, для которых уже записаны уравнения по второму закону Кирхгофа. Такие контуры условимся именовать независящими.
Требование, дабы в каждый новый контур заходила хотя бы одна новенькая ветвь, является достаточным, но не нужным условием, а поэтому его не всегда делают.
Пример 10. Отыскать токи в ветвях схемы рис. 2.9, в какой Е1 = 80 В, Е2 = 64 В, R1 = 6 Ом, R2 = 4 Ом, R3 = 3 Ом, R4 = 1 Ом.
Решение. Произвольно избираем положительные направления тока в ветвях. В схеме рис. 2.9, в = 3; вит = 0; у = 2.
Поэтому, по первому закону Кирхгофа, можно составить только одно уравнение:
Несложно убедиться, что для второго узла получили бы аналогичное уравнение. По второму закону Кирхгофа составим в — вит — (у — 1) = 3 — 0 — (2 — 1) = 2 уравнения. Положительные направления обхода контуров избираем по часовой стрелке.
Символ плюс перед I1R1 взят так как направление тока совпадает с направлением обхода контура; символ минус перед I2R2 — так как направление I2 встречно обходу контура.
Совместное решение уравнений (а) — (в)дает I1 = 14 А, I2 = — 15 А, I3 = — 1 А.
Так как положительные направления токов выбирают произвольно, в итоге расчета какой-нибудь один либо несколько токов возможно окажутся отрицательными. В рассмотренном примере отрицательными оказались токи I2 и I3, что следует осознавать так: действительные направления токов I2 и I3 не совпадают с избранными.
Для выбора контура таким макаром, дабы в любой из них входило по одной ветки, не входящей в другие контуры, применяют понятие дерева. Под деревом понимают совокупа веток, касающихся всех узлов, но не образующих ни 1-го замкнутого контура. При составлении системы уравнений по второму закону Кирхгофа можно взять хоть какое дерево из вероятных.
Тема 5. Попорядку. Возмездное оказание услуг: К адвокату на консультацию явилась Минеева и объяснила, что.