Сила тока в цепи переменного тока

Напряжение в цепи переменного тока меняется по гармоническому закону:

Сила тока в цепи переменного тока меняется по гармоническому закону:

Действующим значением силы переменного тока именуют величину неизменного тока, действие которого произведёт такую же работу , что и переменный ток:

Действующее значение напряжения переменного тока:

Средняя мощность переменного тока на конденсаторе и катушке индуктивности равна нулю, на резисторе определяется через действующие значения:

При последовательном соединении резистора, конденсатора и катушки индуктивности сила тока этих частей одинакова, а напряжение отличается по фазе от силы тока.
Если сила тока меняется по закону:

То на резисторе напряжение меняется синхронно с силой тока:

На конденсаторе напряжение отстает от силы тока на :

На катушке индуктивности напряжение опережает силу тока на :

З-н Ома для резистора :

З-н Ома для конденсатора :

где емкостное сопротивление назад пропорционально частоте и емкости конденсатора:

З-н Ома для катушки индуктивности :

где индуктивное сопротивление прямо пропорционально частоте и индуктивности катушки:

Трансформатор представляет собой две катушки с общим сердечником. При подаче переменного напряжения на первичную обмотку во вторичной появляется напряжение .

Мощность безупречного трансформатора на входе равна мощности на выходе :

Коэффициент трансформации :

Амплитуда силы тока во всей последовательной цепи находится в зависимости от частоты и определяется по формуле:

Переменный электрический ток. Действующее значение силы тока и напряжения. Закон Ома для цепи переменного тока.

Переменный электрический ток – это ток, изменяющийся с течением времени по гармоническому закону (по величине и направлению):

Действующее значение силы тока:

Действующее значение напряжения:

Закон Ома для цепи переменного тока: «Амплитудное (действующее) значение силы тока в цепи переменного тока равно отношению амплитудного (действующего) значения напряжения на концах этой цепи к его полному сопротивлению»:

где – активное сопротивление, Ом;

– индуктивное сопротивление, Ом;

– повторяющаяся частота переменного тока, рад/с;

– индуктивность, Гн;

– емкостное сопротивление, Ом;

– емкость переменного тока, Ф;

– полное сопротивление, Ом;

– амплитудное значение силы тока, А, и напряжения, В.

Свободные электромагнитные колебания в колебательном контуре.

Повторяющиеся колебания электрических зарядов и токов, электрических и магнитных полей именуются электромагнитными колебаниями.

Электрическая цепь, в какой могут происходить электромагнитные колебания, именуется колебательным контуром. Простой закрытый колебательный контур – это соединённые между собой конденсатор и катушка индуктивности.

Дабы в контуре появились электромагнитные колебания, контур нужно вывести из состояния равновесия. Для этого довольно зарядить конденсатор либо возбудить ток в контуре.

В колебательном контуре временами меняются (колеблются) следующие физические величины: q – заряд на обкладках конденсатора; U – разность потенциалов на конденсаторе и, поэтому, на концах катушки; i – ток в катушке; и – напряжённость электрического и индукция магнитного поля; и – энергия электрического и магнитного полей.

Заряд на обкладках конденсатора меняется по гармоническому закону.

Собственные незатухающие колебания:

где – заряд, Кл;

– амплитудное значение заряда, Кл;

– исходная фаза;

– угловая частота колебаний (собственная частота), рад/с;

– время, с;

– фаза гармонических колебаний.

Период собственных колебаний контура:

где – индуктивность, Гн;

– емкость, Ф.

Частота собственных колебаний:

Собственные затухающие колебания не являются гармоническими:

где – исходная амплитуда заряда, Кл.

– коэффициент затухания.

:

где – активное сопротивление, Ом.

Логарифм отношений 2-ух последующих амплитуд, отличающихся на период, именуется логарифмическим декрементом затухания:

Время релаксации затухающих колебаний – время, в течение которого амплитуда колебаний миниатюризируется в e раз:

Коэффициент затухания – это величина, оборотная времени, в течение которого амплитуда колебаний миниатюризируется в e раз.

Логарифмический декремент затухания – это величина, оборотная числу колебаний, совершаемых за время релаксации:

Добротность контура есть умноженное на π число полных колебаний, по истечении которых амплитуда миниатюризируется в e раз:

Механическое удерживание земельных масс: Механическое удерживание земельных масс на склоне обеспечивают контрфорсными сооружениями разных конструкций.

Папиллярные узоры пальцев рук — маркер спортивных возможностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не меняются в течение жизни.

Опора древесной одностоечной и методы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на нужной высоте над землей, водой.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особенное значение присваивают эстетическим.

Действующее значение силы тока и напряжения

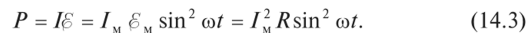
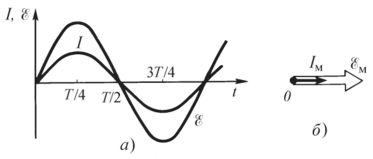
включающая сопротивление подводящих проводов. В цепи с активной нагрузкой — резистором — колебания силы тока, э.д.с. и напряжения происходят в одной фазе [см. (14.1) и (14.2)]. Моментальная мощность (мощность в каждый данный момент времени) [см. (9.30)]

График этой функции показан на рис. 14.3. Для сопоставления тут же штрихом изображен график силы тока. Амплитуда мощности

2. Вычислим среднюю мощность переменного тока за период времени Т. Для этого следует работу, совершенную током за этот период времени (по другому — выделившуюся за этот период времени джоулеву теплоту), поделить на период. Для вычисления работы воспользуемся рис. 14.3.

Из определения мощности следует, что простая работа ЪА = pAt, а полная работа изображается площадью под графиком. Из характеристики синусоиды следует, что площадь, заштрихованная под кривой, равна площади прямоугольника, основание которого равно периоду, а высота — половине амплитуды мощности. Итак, за период Т работа

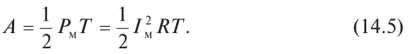
Средняя мощность [см. (9.29)]

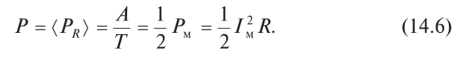
• 3. Сравнив выражение (14.6) с формулой для вычисления мощности неизменного тока P=I [1][2] R [см. (9.30)], получим
• 1 / [2]

I [2] R = -I [2] UR. Отсюда следует, что / [2] = и

Поэтому, переменный ток с амплитудой /м по собственному термическому (либо механическому) действию эквивалентен неизменному току -рг. Данную величину именуют действующим значени-

ем силы переменного тока. Соответственно величины

именуют действующими значениями э.д.с. и напряжения.

Большая часть электроизмерительных устройств, применяемых для измерений в цепях переменного тока, градуируют так, что они демонстрируют действующие значения измеряемых величин.

Цепи переменного тока с индуктивностью и электроемкостью

Соединим последовательно резистор — лампу накаливания сопротивлением R, конденсатор емкостью С и катушку большой индуктивности L (рис. 14.4). Если данную цепь присоединить к зажимам генератора переменного тока, то лампа зажгется, что свидетельствует о наличии электрического тока в цепи, невзирая на разрыв, имеющийся между изолированными друг от друга обкладками конденсатора. Для переменного тока это разъясняется следующим образом.

В данной цепи действует переменная, сделанная наружным источником — генератором, э.д.с. ? = ?м sin со/. Дальше действует

э.д.с. самоиндукции ?? =—[см. (12.8)]. В конце концов, действует

переменная разность потенциалов ф, -ф2 = Q [см. (8.19)], возникающая за счет зарядов, скапливающихся на пластинках конденсатора.

На базе закона Ома для неоднородного участка цепи (9.18) имеем

Данное выражение можно конвертировать к виду

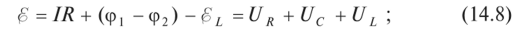
тут разность потенциалов на резисторе с активным сопротивлением

на конденсаторе на катушке индуктивности

Итак, секундное значение наружной э.д.с. равно моментальному значению результирующей разности потенциалов, колеблющейся с частотой наружной э.д.с.:

2. Выражение (14.8) показывает на то, что в цепях переменного тока заместо 1-го резистора с активным сопротивлением мы рассматриваем действие одной наружной э.д.с. на три сопротивления: активное R и два так именуемых реактивных — емкостное Хс и индуктивное XL, которые, как будет показано ниже, коренным образом отличаются как друг от друга, так и от активного сопротивления. Таковой подход к анализу явлений в цепях переменного тока очень комфортен. Его обширно используют в электротехнике.

Если подключить вертикально отклоняющие пластинки осциллографа к резистору, конденсатору и катушке, то можно следить гармонические колебания разности потенциалов на их концах. Как свидетельствует опыт, фазы колебаний на отдельных участках отличаются друг от друга. Разность фаз 2-ух колебаний именуют сдвигом фаз. Изучим несколько подробнее каждый участок цепи в отдельности.

• 3. Поначалу разглядим цепь, в какой падением напряжения на конденсаторе и катушке можно пренебречь по сопоставлению с падением напряжения на резисторе (т. е. Uc « UR и UL « UR). Тогда выражение (14.8) воспримет вид ё = IR, т. е. мы вернемся к соотношению (14.2). А это означает, что колебания силы тока и напряжения (э.д.с.) в цепи с активным сопротивлением, как это уже было отмечено, происходят в одной и той же фазе.
• * 4. Величины, изменяющиеся по синусоидальному закону, можно изображать при помощи графиков, как мы это делали выше. Но в теории колебаний и в электротехнике обширно используют и другой, очень обычной и приятный метод изображения гармонических функций, получивший название способа векторных диаграмм. Суть этого способа состоит в следующем. Амплитуды (либо действующие значения) величин условно считают векторами и строят эти векторы так, дабы углы между ними, отсчитанные против часовой стрелки, были равны сдвигам фаз между колебаниями значений соответственных величин.

Какой из векторов принять за базовый (т. е. таковой, относительно которого отсчитываются фазы колебаний), находится в зависимости от условия определенной задачи. К примеру, если сила тока во всех участках цепи одинакова (при последовательном соединении), то в качестве базового выбирают вектор силы тока. Если же на всех участках цепи одинаковы напряжения (параллельное соединение), то в качестве базового выбирают вектор напряжения.

Ниже мы увидим необыкновенную ценность способа векторных диаграмм при суммировании колебаний с равными частотами, но отличающихся фазами, так как суммирование осуществляется по правилу сложения векторов.

Для цепи с активным сопротивлением графики силы тока и напряжения и соответственная векторная диаграмма показаны на рис. 14.5, а, б соответственно. *

5. Сейчас соберем цепь, аналогичную изображенной на рис. 14.4, в какой нет катушки (UL = 0), а емкость батареи конденсаторов и сопротивление лампы накаливания подобраны так, что Uc» UR. Мы получим цепь с емкостным сопротивлением. Опыты демонстрируют, что колебания силы тока в цепи с емкостным сопротивлением представляют собой гармонические колебания с частотой, равной частоте вынуждающей э.д.с. Но в отличие от цепи с активным сопротивлением, где фазы колебаний силы тока и э.д.с. совпадают, тут наблюдается сдвиг по фазе между колебаниями наружной э.д.с. и силы тока: в цепи с емкостным сопротивлением колебания силы тока опережают колебания наружной э.д.с. по фазе на к/2.

Естественно, точно так же можно утверждать, что колебания э.д.с. отстают от колебаний силы тока по фазе на тот же угол. Временная и векторная диаграммы для данного варианта приведены на рис. 14.6, а, б соответственно.

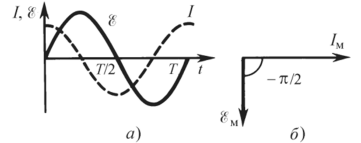
Опыт указывает также, что конденсатор ведет себя в цепи переменного тока как некоторое сопротивление, ограничивающее амплитуду (и действующее значение) силы тока. Емкостное сопротивление

где С — электроемкость конденсатора, а со — радиальная частота переменного тока.

* 6. Выражение для емкостного сопротивления несложно вывести.

Опыт указывает, что сила тока и напряжение изменяются по закону синуса и смещены по фазе на п/2. Если так, то, как было установлено выше [см. (13.11)], /м = соCUM. Отсюда емкостное сопротивление

7. Соберем цепь, аналогичную изображенной на рис. 14.4, но без конденсатора, а активное сопротивление и индуктивность катушки подберем такими, дабы UL » UR. Мы получим цепь с индуктивным сопротивлением.

Опыт указывает, что колебания силы тока в цепи с индуктивным сопротивлением представляют собой гармонические колебания с частотой, равной частоте вынуждающей э.д.с., точь-в-точь как в цепи с активным и емкостным сопротивлениями. Итак, мы получаем общий вывод: частота принужденных колебаний тока равна частоте вынуждающей э.д.с. независимо от параметров электрической цепи. Этим обязанные колебания принципно отличаются от свободных колебаний и автоколебаний (см. гл. 13).

Заметим, что данное свойство принужденных колебаний справедливо не только лишь для электрических цепей, но и для механических колебательных систем.

Опыт также указывает, что в цепи с индуктивным сопротивлением колебания силы тока отстают по фазе на к/2 от колебаний наружной э.д.с., либо, что то же самое, колебания э.д.с. опережают колебания силы тока на тот же угол. Для данного варианта на рис. 14.7, а, б изображены соответственно временная и векторная диаграммы.

В конце концов, из опыта следует, что катушка с индуктивностью L ведет себя в цепи переменного тока с радиальный частотой со как некоторое сопротивление, ограничивающее амплитуду (и действующее значение) силы тока. Индуктивное сопротивление

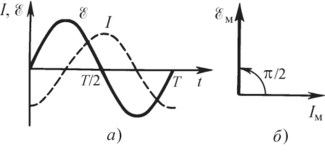
# 8. Выражение для индуктивного сопротивления можно вывести аналогично тому, как это было изготовлено выше для емкостного сопротивления.

В данном случае, полагая, что UR= Uc= 0, из (14.8) и (14.11) имеем

Для вывода формулы (14.13) применим применяемый нами ранее при выводе формулы своей частоты [см. (13.10)] способ аналогий.

Опыт указывает, что напряжение U L на концах соленоида и сила тока / в нем подчиняются закону синуса и что они смещены по фазе на ^ . В связи с этим опять, как и ранее, воспользуемся тем, что формула ускорения

[см. (13.5)] подобна формуле

Тут изменение силы тока аналогично изменению скорости. Но, как мы установили ранее, /м = со0м. Подставив это в предшествующее выражение, имеем

Видео: Конденсатор в цепи переменного тока