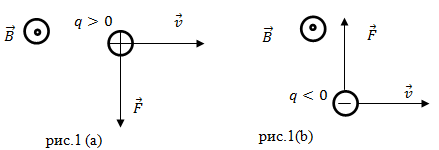
1. Пусть в однородное магнитное поле влетает положительный заряд q со скоростью v перпендикулярно линиям индукции магнитного поля (рис. 11.9). Опыт указывает, что в данном случае заряженная частичка движется по окружности в плоскости, перпендикулярной линиям индукции. А это означает, что на частичку дей-
ствует сила F =-, перпендикулярная вектору скорости v и
направленная к центру окружности [см. (2.15)].
Исследуя в вакууме зависимость этой силы от заряда q частички, скорости ее движения v и параметров магнитного поля, характеризующихся векторной величиной В, Лоренц установил, что сила, с которой магнитное поле действует на перемещающийся заряд, определяется по формуле
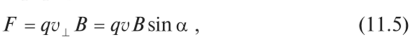
где а — угол между направлением полосы индукции магнитного поля и вектором скорости. Эту силу именуют силой Лоренца.
2. Направление силы Лоренца можно найти при помощи правила левой руки: если расположить левую руку так, дабы силовая линия индукции заходила в ладонь, а вектор v был ориентирован вдоль 4 пальцев, то отставленный большой палец покажет направление силы F, с которой магнитное поле действует на положительный заряд q (рис. 11.9). На отрицательный заряд, перемещающийся в том же направлении и в таком же магнитном поле, действует обратно направленная сила.
Опыт указывает также, что если заряд движется вдоль линий индукции поля, т. е. если вектор скорости и полосы индукции поля параллельны либо антипараллельны (т. е. а = 0 либо а = к), то магнитное поле на этот заряд не действует.
Необходимо подчеркнуть одно принципиальное событие: магнитная сила, т. е. сила Лоренца, работы не совершает. Вправду, согласно определению (2.28), простая работа ЬА = FAl cos р, где (3 — угол между направлением силы и направлением перемещения. Но сила Лоренца перпендикулярна перемещению заряда: F±v; поэтому, р = ^ и
* 3. Заметим, что формула (11.5) вытекает из (11.4), если положить Q2 = q, a
Таким макаром, мы приходим к выводу, что появление магнитного взаимодействия между перемещающимся зарядом и магнитным полем есть релятивистский эффект, происходящий при всех, даже сколь угодно малых, скоростях. Другими словами, правильное описание электромагнитных явлений дает не традиционная (ньютоновская) механика, а теория относительности. #
4. Подобно тому как для силовой свойства электрического поля была введена векторная величина — напряженность поля (8.3), в качестве силовой свойства магнитного поля вводится векторная величина В, именуемая индукцией магнитного поля либо просто индукцией. Индукцию магнитного поля в вакууме обозначают В0.
Если напряженность электрического поля пропорциональна покоящемуся заряду, с которым оно связано, то индукция магнитного поля пропорциональна перемещающемуся заряду, с которым связано магнитное поле, т. е. пропорциональна силе тока, создающего магнитное поле (В~1).
Вектор индукции магнитного поля можно найти через действие магнитной силы на перемещающийся с некоторой скоростью заряд, аналогично тому, как определяется напряженность электрического поля через действие электрической силы, но лишь на покоящийся заряд. На основании (11.5) модуль вектора индукции магнитного поля равен отношению магнитной силы F к произведению заряда q на его скорость v при условии, что заряд движется перпендикулярно вектору индукции:

Вектор индукции ориентирован по касательной к полосы индукции в согласовании с правилом буравчика (см. § 11.2).
В СИ единицу индукции магнитного поля именуют тесла (Тл); Тл — это индукция поля, которое действует с силой 1 Н на заряд 1 Кл, перемещающийся перпендикулярно линиям индукции со скоростью 1 м/с:
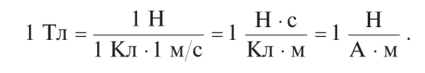
# 5. Вместе с вектором индукции часто применяется еще одна векторная черта магнитного поля — напряженность.
Напряженностью Я магнитного поля именуют величину

где В0 — индукция магнитного поля в вакууме, а неизменный коэффициент [см. (11.4)]

получил название магнитной неизменной.
Напряженность магнитного поля — вектор. Его направление совпадает с направлением вектора индукции магнитного поля.
В СИ единицей напряженности магнитного поля является ампер на метр (А/м):
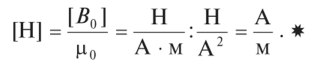
6. Принципиальной чертой магнитного поля является скалярная величина, именуемая магнитным потоком Ф.
Пусть плоская поверхность площадью S размещена в однородном магнитном поле (рис. 11.10). Магнитным потоком Ф через поверхность площадью S именуют произведение, равное проекции В± вектора индукции В на нормаль п к поверхности и
площади этой поверхности:
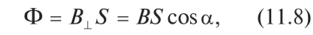
где а — угол между направлением вектора В и положительной нормалью к площадке.
В СИ единицу магнитного потока именуют вебер (Вб): 1 Вб — магнитный поток, пронизываю-
щий поверхность площадью 1 м 2 , расположенную перпендикулярно линиям индукции однородного магнитного поля с индукцией 1 Тл:
2. Сила Лоренца
Сила Лоренца—сила, с которой, в пределахтрадиционной физики,электромагнитное поледействует наточечнуюзаряженнуючастичку. Силой Лоренца именуют время от времени силу, действующую на перемещающийся со скоростьюзарядлишь со сторонымагнитного поля, часто же полную силу — со стороны электромагнитного поля вообщем [1] по другому говоря, со стороныэлектрическогоимагнитногополей в системеСИ:
Названа в честь голландского физикаХендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найденоХевисайдом [2] .
Личным случаем силы Лоренца является сила Ампера.
3. Закон Ампера
Зако́н Ампе́ра— закон взаимодействия неизменныхтоков. УстановленАндре Мари Амперомв1820. Из закона Ампера следует, что параллельныепроводникис неизменными токами, текущими в одном направлении, притягиваются, а в обратных — отталкиваются. Законом Ампера именуется также закон, определяющий силу, с котороймагнитное поледействует на малый отрезок проводника с током. Сила, с которой магнитное поле действует на элемент объёмаdVпроводника с током плотности, находящегося в магнитном поле с индукцией:
.
Если ток течёт по узкому проводнику, то , где— «элемент длины» проводника — вектор, по модулю равныйdlи совпадающий по направлению с током. Тогда предшествующее равенство можно переписать следующим образом:
Направление силы определяется по правилу вычислениявекторного произведения, которое комфортно уяснить с помощьюправила левой руки.
Модуль силы Ампера можно отыскать по формуле:
,
где α — угол между векторами магнитной индукции и тока.
Сила dFмаксимальна когда элемент проводника с током размещен перпендикулярно линиям магнитной индукции ():
.
4. Аксиома Гаусса для магнитного поля в вакууме (инт. И дифф. Вид)
Аксиома Гаусса— основная аксиомаэлектродинамики, которая применяется для вычисления электрических полей, заходит в системууравнений Максвелла. Она выражает связь между потоком напряжённости электрического поля через замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью.
Общая формулировка:Поток векторанапряжённости электрического полячерез всякую, произвольно избранную замкнутую поверхность пропорционален заключённому снутри этой поверхностиэлектрическому заряду.
— поток вектора напряжённости электрического поля через замкнутую поверхностьS.
Q— полный заряд, находящийся в объёме, который ограничивает поверхностьS.
—электрическая неизменная.
Данное выражение представляет собой аксиому Гаусса в интегральной форме.
В дифференциальной форме аксиома Гаусса выражается следующим образом:
Тут ρ — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а —оператор набла.
Для аксиомы Гаусса справедлив принцип суперпозиции, другими словами поток вектора напряжённости через поверхность не находится в зависимости от рассредотачивания заряда снутри поверхности.
Физической основой аксиомы Гаусса является закон Кулоналибо, по другому, аксиома Гаусса является интегральной формулировкойзакона Кулона.
5. Аксиома о циркуляции для магнитного поля в вакууме (инт. И дифф. Вид)
Поясним понятие циркуляциивектораПусть в пространстве, где сотворено магнитное поле, избран некоторый условный замкнутый контур (не непременно тонкий) и обозначено положительное направление его обхода. На каждом отдельном малом участке Δlэтого контура можно найти касательную составляющуювекторав данном месте, другими словами найти проекцию векторана направление касательной к данному участку контура (рис. 1.17.2).
Замкнутый контур (L) с данным направлением обхода. Изображены токиI1,I2иI3, создающие магнитное поле
Циркуляцией вектора именуют сумму произведенийΔl, взятую по всему контуруL:
Некоторые токи, создающие магнитное поле, могут пронизывать избранный контур Lв то время, как другие токи могут находиться в стороне от контура.
Аксиомаоциркуляцииутверждает, что циркуляция векторамагнитногополянеизменных токов по хоть какому контуруLвсегда равна произведению магнитной неизменной μ0на сумму всех токов, пронизывающих контур:
В качестве примера на рис. 1.17.2 изображены несколько проводников с токами, создающими магнитное поле. Токи I2иI3пронизывают контурLв обратных направлениях, им должны быть приписаны различные знаки – положительными числятся токи, которые связаны с избранным направлением обхода контура правилом правого винта (буравчика). Поэтому,I3> 0, аI2< 0. ТокI1не пронизывает контурL.
Аксиомаоциркуляциив данном примере выражается соотношением:
Аксиомаоциркуляциив общем виде следует из закона Био–Савара и принципа суперпозиции.
Простым примером использования аксиомы о циркуляцииявляется вывод формулы для магнитной индукцииполяпрямолинейного проводника с током. Беря во внимание симметрию в данной задачке, контурLцеленаправлено избрать в виде окружности некоторого радиусаR, лежащей в перпендикулярной проводнику плоскости. Центр окружности находится в некоторой точке проводника. В силу симметрии векторнаправлен по касательной, а его модуль одинаков во всех точках окружности. Использование аксиомы оциркуляцииприводит к соотношению:
откуда следует формула для модуля магнитной индукции поляпрямолинейного проводника с током, приведенная ранее.
Этот пример указывает, что аксиомаоциркуляциивектора магнитной индукцииможет быть применена для расчета магнитных полей, создаваемых симметричным рассредотачиванием токов, когда из суждений симметрии можно «угадать» общую структуруполя.
Имеется много фактически принципиальных примеров расчета магнитных полей при помощи аксиомы о циркуляции. Одним из таких примеров является задачка вычисленияполятороидальной катушки
Сила Лоренца. Правило левой руки

Опыты демонстрируют, что на заряд, перемещающийся в магнитном поле, со стороны этого поля действует сила, которая именуется силой Лоренца. Разглядим коротко особенности этой силы.
Открытие силы Лоренца
Магнитное поле не ведет взаимодействие с покоящимися зарядами, и длительное время связь между магнитными и электрическими явлениями не обнаруживалась. В первый раз такую связь — воздействие проводника с током на стрелку компаса — нашел в первой половине XIX в. Х. Эрстед. Оборотное явление — воздействие поля магнита на проводник с током (также взаимодействие 2-ух проводников с током) — было открыто скоро А. Ампером.
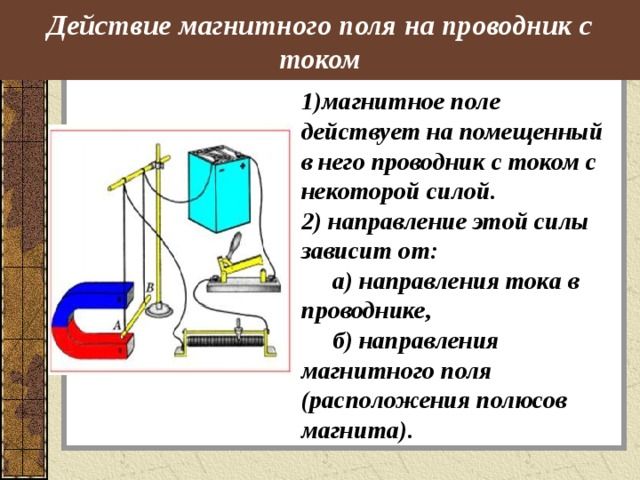
Рис. 1. Действие магнитного поля на проводник с током.
Но механизм появления силы Ампера был исследован только к концу XIX в. К этому времени стало ясно, что электрический ток — это упорядоченное движение заряженных частиц. Поэтому, сила Ампера появляется из-за того, что магнитное поле оказывает силовое воздействие на перемещающиеся заряды.
Такая сила была найдена Х. Лоренцем. Он же вывел ее формулу.
Особенности силы Лоренца
Так как сила Лоренца — это сила, действующая на перемещающийся заряд в магнитном поле, то ее величина находится в зависимости от всех 3-х значений: от величины заряда, от скорости и от индукции магнитного поля:
$$F_L = qvB sin \alpha$$
Но в формулу заходит очередной параметр — угол $\alpha$, характеризующий направление силы Лоренца. Это угол между направлением движения носителя заряда (вектором его скорости) и вектором магнитной индукции.
Дело в том, что в отличие от многих других сил, направление силы Лоренца не совпадает ни с направлением движения носителя заряда, ни с направлением на источник магнитного поля, а ее появление находится в зависимости от обоюдного направления магнитного поля и скорости движения заряда. Сила Лоренца перпендикулярна плоскости, образуемой векторами магнитной индукции и скорости движения заряда.
Направьте внимание, что, если направление движения заряда и направление линий магнитной индукции совпадают, то угол $\alpha$ равен нулю, и сила Лоренца отсутствует.

Рис. 2. Сила Лоренца.
Правило левой руки
Для силы Лоренца правило левой руки формулируется следующим образом.
Если четыре вытянутых пальца левой руки указывают направление движения положительного заряда, а полосы магнитного поля входят в ладонь, «прокалывая» ее, то отставленный большой палец покажет направление силы Лоренца.
Разглядим, как работает для определения силы Лоренца правило левой руки. Допустим, электрон движется «на нас», впереди вспять, северный магнитный полюс размещен справа, а южный — слева. Куда ориентирована сила Лоренца?
Правило сформулировано для положительного заряда, к примеру, для протона. Электрон заряжен негативно, поэтому, четыре вытянутых пальца левой руки должны быть ориентированы против его движения — вперед.
Полосы магнитного поля ориентированы от северного к южному полюсу, другими словами справа влево. Располагаем левую руку так, дабы эти полосы входили в ладонь. Четыре вытянутых пальца как и раньше ориентированы вперед, другими словами ладонь лежит на столе «на ребре», 4-мя пальцами вперед.
Отставленный большой палец будет ориентирован ввысь. Таким макаром, на электрон будет действовать сила Лоренца, направленная ввысь.
Для закрепления правила левой руки можно придумать другие примеры с другими направлениями.
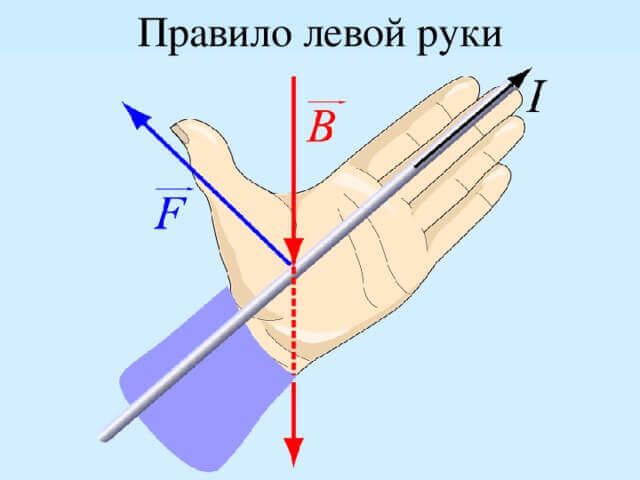
Рис. 3. Правило левой руки.
Что мы узнали?
На заряд, перемещающийся в магнитном поле, действует сила Лоренца. Величина этой силы пропорциональная величине заряда, его скорости, индукции магнитного поля и находится в зависимости от обоюдной направленности этих векторов. Для определения направления силы Лоренца применяется правило левой руки.