может быть выражена через силы, действующие на отдельные носители заряда.
Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение n q υ S, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S – площадь поперечного сечения проводника, равно току, текущему по проводнику:
Выражение для силы Ампера можно записать в виде:
Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно n S Δl, то сила, действующая на одну заряженную частичку, равна
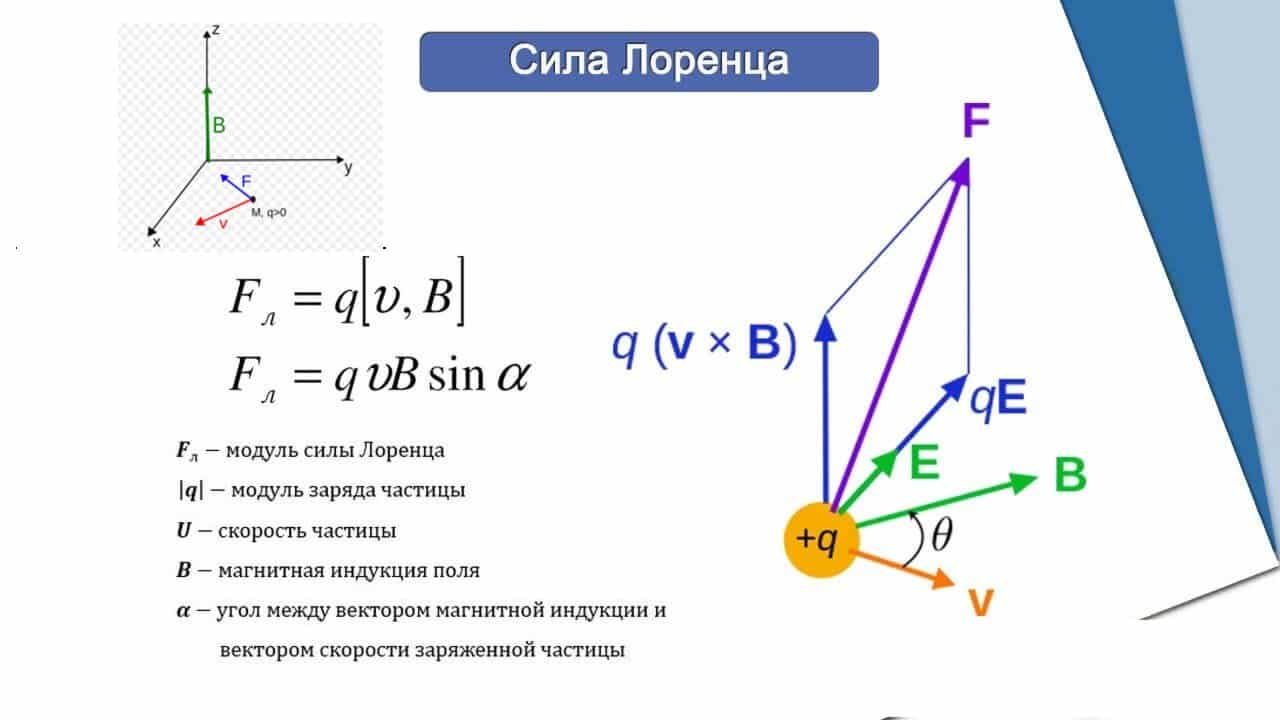
Эту силу именуют силой Лоренца. Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции . Направление силы Лоренца, действующей на положительно заряженную частичку, так же, как и направление силы Ампера, может быть найдено по правилу левой руки либо по правилу буравчика. Обоюдное размещение векторов , и для положительно заряженной частички показано на рис. 1.18.1.
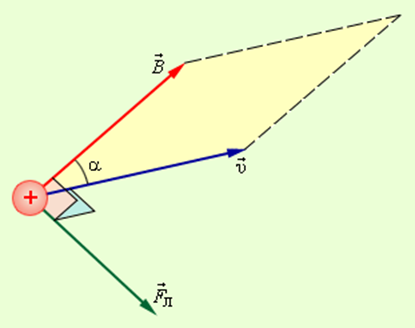
Обоюдное размещение векторов , и Модуль силы Лоренца численно равен площади параллелограмма, построенного на векторах и помноженной на заряд q
Сила Лоренца ориентирована перпендикулярно векторам и
При движении заряженной частички в магнитном поле сила Лоренца работы не совершает. Потому модуль вектора скорости при движении частички не меняется.
Если заряженная частичка движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору то частичка будет двигаться по окружности радиуса
Сила Лоренца в данном случае играет роль центростремительной силы (рис. 1.18.2).
Радиальное движение заряженной частички в однородном магнитном поле
Период воззвания частички в однородном магнитном поле равен
Это выражение указывает, что для заряженных частиц данной массы m период воззвания не находится в зависимости от скорости υ и радиуса линии движения R.
Угловая скорость движения заряженной частички по радиальный линии движения
именуется циклотронной частотой. Циклотронная частота не находится в зависимости от скорости (поэтому, и от кинетической энергии) частички. Это событие применяется в циклотронах – ускорителях томных частиц (протонов, ионов). Принципная схема циклотрона приведена на рис. 1.18.3.
Движение заряженных частиц в вакуумной камере циклотрона
Между полюсами сильного электромагнита помещается вакуумная камера, в какой находятся два электрода в виде полых железных полуцилиндров (дуантов). К дуантам приложено переменное электрическое напряжение, частота которого равна циклотронной частоте. Заряженные частички инжектируются в центре вакуумной камеры. Частички ускоряются электрическим полем в промежутке между дуантами. Снутри дуантов частички движутся под действием силы Лоренца по полуокружностям, радиус которых вырастает по мере роста энергии частиц. Всякий раз, когда частичка пролетает через зазор между дуантами, она ускоряется электрическим полем. Таким макаром, в циклотроне, как и во всех других ускорителях, заряженная частичка ускоряется электрическим полем, а удерживается на линии движения магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ.
Однородные магнитные поля применяются в почти всех устройствах и, а именно, в масс-спектрометрах – устройствах, при помощи которых можно определять массы заряженных частиц – ионов либо ядер разных атомов. Масс-спектрометры применяются для разделения изотопов, другими словами ядер атомов с одинаковым зарядом, но различными массами (к примеру, 20 Ne и 22 Ne). Простой масс-спектрометр показан на рис. 1.18.4. Ионы, вылетающие из источника S, проходят через несколько маленьких отверстий, формирующих узенький пучок. Потом они попадают в селектор скоростей, в каком частички движутся в скрещенных однородных электрическом и магнитном полях. Электрическое поле создается между пластинами плоского конденсатора, магнитное поле – в зазоре между полюсами электромагнита. Исходная скорость заряженных частиц ориентирована перпендикулярно векторам и
На частичку, перемещающуюся в скрещенных электрическом и магнитном полях, действуют электрическая сила и магнитная сила Лоренца. При условии E = υB эти силы точно уравновешивают друг дружку. Если это условие осуществляется, частичка будет двигаться умеренно и прямолинейно и, пропархав через конденсатор, пройдет через отверстие в экране. При данных значениях электрического и магнитного полей селектор выделит частички, перемещающиеся со скоростью υ = E / B.
Дальше частички с одним и этим же значением скорости попадают в камеру масс-спектрометра, в какой сотворено однородное магнитное поле . Частички движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Линии движения частиц представляют собой окружности радиусов R = mυ / qB’. Измеряя радиусы траекторий при узнаваемых значениях υ и B’ можно найти отношение q / m. В случае изотопов (q1 = q2) масс-спектрометр позволяет поделить частички с различными массами.
Современные масс-спектрометры позволяют определять массы заряженных частиц с точностью выше 10 –4 .
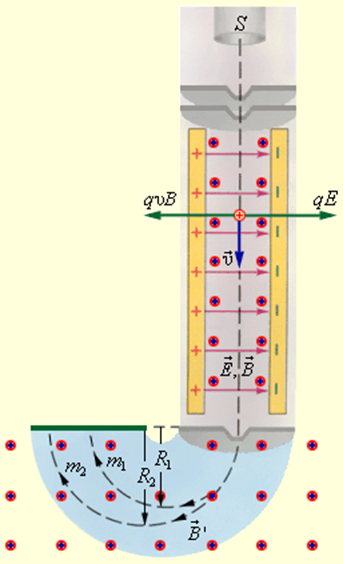
Селектор скоростей и масс-спектрометр
Если скорость частички имеет составляющую вдоль направления магнитного поля, то такая частичка будет двигаться в однородном магнитном поле по спирали. При всем этом радиус спирали R находится в зависимости от модуля перпендикулярной магнитному полю составляющей υ+ вектора а шаг спирали p – от модуля продольной составляющей υ|| (рис. 1.18.5).
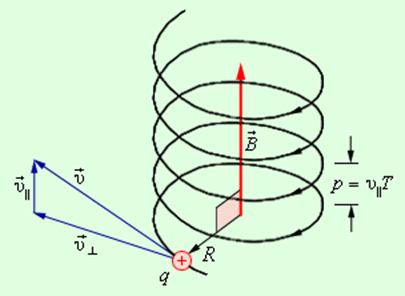
Движение заряженной частички по спирали в однородном магнитном поле
Таким макаром, линия движения заряженной частички вроде бы навивается на полосы магнитной индукции. Это явление применяется в технике для магнитной теплоизоляции высокотемпературной плазмы, другими словами вполне ионизированного газа при температуре порядка 10 6 K. Вещество в таком состоянии получают в установках типа «Токамак» при исследовании управляемых термоядерных реакций. Плазма не должна соприкасаться со стенами камеры. Теплоизоляция достигается методом сотворения магнитного поля специальной конфиругации. В качестве примера на рис. 1.18.6 изображена траектория перемещения заряженной частички в магнитной «бутылке» (либо ловушке).
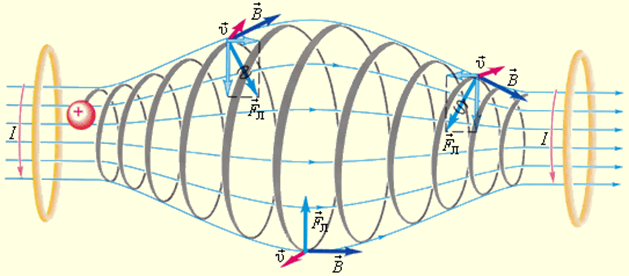
Магнитная «бутылка». Заряженные частички не выходят за границы «бутылки». Магнитное поле «бутылки» может быть сотворено при помощи 2-ух круглых катушек с током
Аналогичное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического места. Резвые заряженные частички из космоса (приемущественно от Солнца) «захватываются» магнитным полем Земли и образуют так именуемые радиационные пояса (рис. 1.18.7), в каких частички, как в магнитных ловушках, передвигаются туда и назад по спиралеобразным траекториям между северным и южным магнитными полюсами за времена порядка толикой секунды. Только в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния. Радиационные пояса Земли простираются от расстояний порядка 500 км до 10-ов земных радиусов. Следует вспомнить, что северный магнитный полюс Земли на данный момент находится поблизости северного географического полюса и равномерно перемещается. Природа земного магнетизма до сего времени не исследована.
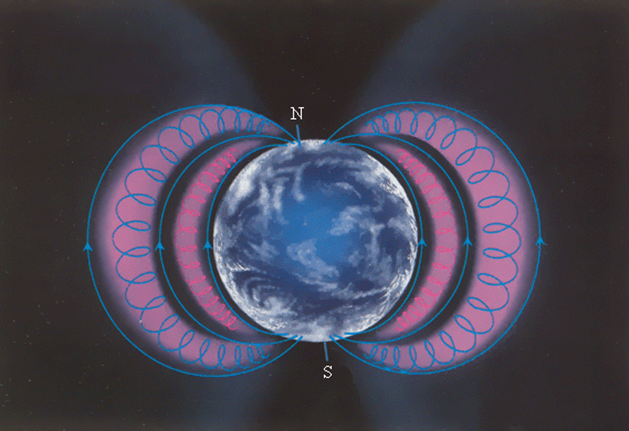
Радиационные пояса Земли. Резвые заряженные частички от Солнца (в главном электроны и протоны) попадают в магнитные ловушки радиационных поясов. Частички могут покидать пояса в полярных областях и вторгаться в верхние слои атмосферы, вызывая полярные сияния
Сила Лоренца
Как уже было сказано ранее, магнитное поле действует на перемещающийся заряд. В ряде тестов было показано, что при влёте в магнитное поле заряженной частички, её линия движения искривляется (т.е. отклоняется от прямой). Вследствие познания второго закона Ньютона и наличия центростремительного ускорения (т.к. тело движется по кривой), такое движение разъясняется наличием силы — силы Лоренца.
Значение модуля этой силы:
- где
- — сила Лоренца,
- — заряд, перемещающийся в магнитном поле,
- — скорость заряженной частички,
- — модуль вектора магнитной индукции,
- — синус угла между направлением скорости и направлением вектора магнитной индукции.
Рис. 1. Сила Лоренца
Направление силы Лоренца — перпендикуляр к касательной линии движения (т.е. перпендикуляр к скорости на этот момент). Но в плоскости рисунка вероятны два направления для перпендикуляра. Какое из них избрать — вопрос заряда и правила левой руки. Пусть положительный заряд влетает в магнитное поле перпендикулярно линиям магнитной индукции () со скоростью . Поле ориентировано перпендикулярно поверхности «на нас». Тогда, согласно правилу левой руки, сила Лоренца ориентирована как показано на рисунке 1. Предстоящее движение заряда, в нашем случае, — движение по окружности.
В случае, если перемещающийся заряд будет отрицательным, направление силы меняется на обратное.
Правило левой руки для силы Лоренца: ориентируем руку так, дабы полосы магнитной индукции входили в ладонь. Четыре пальца руки сонаправляем с вектором скорости частички, тогда противопоставленный большой палец показывает на направление силы Лоренца для положительно заряженной частички. Направление силы Лоренца для негативно заряженной частички обратно.
Задачи на силу Лоренца можно условно поделить на два типа:
- направление скорости перпендикулярна линиям магнитной индукции (тогда задачка сводится к записи второго закона Ньютона и плану решения задач по динамике) и практически рисунка 1,
- направление скорости составляет угол с линиями магнитной индукции. Тогда заряженное тело будет двигаться по спирали (рис. 2).
Рис. 2. Сила Лоренца (Спираль)
Для решения второго типа задач рассматривается логика движения тела, брошенного под углом к горизонту. Т.е. на уровне мыслей разделяем движение на две оси (вдоль и перпендикулярно полю) и анализируем движение: одно — движение по окружности, 2-ое — прямолинейное.
Вывод: задачи на силу Лоренца (1) фактически схожи друг дружке. Обычно решаются через 2-ой закон Ньютона и определение центростремительного ускорения. Нужно чётко различать задачи, в каких частичка движется в магнитном поле перпендикулярно линиям магнитной индукции (тогда тело движется по окружности) либо влетает в поле под углом к линиям магнитной индукции (тогда частичка движется по винтообразной линии движения).
Сила Лоренца
ГОСТ
Определение силы магнитной силы
Если заряд движется в магнитном поле, то на него действует сила ($\overrightarrow$), которая находится в зависимости от величины заряда (q), скорости движения частички ($\overrightarrow$) относительно магнитного поля, и индукции магнитного поля ($\overrightarrow$). Эта сила была установлена экспериментально, именуется она магнитной силой.
И имеет в системе СИ вид:
Модуль силы в согласовании с (1) равен:
где $\alpha $ — угол между векторами $\overrightarrowи\ \overrightarrow$. Из уравнения (2) следует, что если заряженная частичка движется вдоль полосы магнитного поля, то не испытывает деяния магнитной силы.
Направление магнитной силы
Магнитная сила, исходя из (1) ориентирована перпендикулярно плоскости, в какой лежат векторы $\overrightarrowи\ \overrightarrow$. Ее направление совпадает с направлением векторного произведения $\overrightarrowи\ \overrightarrow$ в этом случае, если величина перемещающегося заряда больше нуля, и ориентирована в обратную сторону, если $q
Характеристики силы магнитной силы
Магнитная сила работы над частичкой не свершает, так как обычно ориентирована перпендикулярно скорости ее движения. Из этого утверждения следует, что при помощи воздействия на заряженную частичку при помощи неизменного магнитного поля ее энергию поменять нельзя.
Сила Лоренца
Если на частичку, владеющую зарядом, действуют сразу электрическое и магнитное поля, то равнодействующая сила может быть записана как:
Сила, обозначенная в выражении (3) именуется силой Лоренца. Часть $q\overrightarrow$ является силой, действующей со стороны электрического поля на заряд, $q\left[\overrightarrow\overrightarrow\right]$ охарактеризовывает силу деяния магнитного поля на заряд. Сила Лоренца проявляется при движении электронов и ионов в магнитных полях.
Задание: Протон ($p$) и электрон ($e$), ускоренный одинаковой разностью потенциалов влетают в однородное магнитное поле. Во сколько раз радиус кривизны траектории перемещения протона $R_p$отличается от радиуса кривизны линии движения электрона $R_e$. Углы, под которыми влетают частички в поле, одинаковы.
Если действием силы тяжести в сопоставлении с действием магнитной силы пренебречь, то 2-ой закон Ньютона запишем как:
В формуле (1.1) мы учли, что вектор магнитной составляющей силы Лоренца перпендикулярен скорости и, поэтому, докладывает заряженной частичке обычное ускорение ($a_n$). Его мы можем выразить как:
По условию задачи заряженные частички до попадания в магнитное поле ускоряются электрическим полем, для того, дабы выяснить скорость, с которой частички влетают и движутся в магнитном поле, запишем из закона сохранения энергии:
Из формулы (1.3) выразим скорость движения частички:
Подставим (1.2), (1.4) в (1.1), выразим радиус кривизны линии движения:
Подставим данные для различных частиц, найдем отношение $\frac$:
Заряды протона и электрона по модулю равны. Масса электрона $m_e=9,1\cdot ^кг,m_p=1,67\cdot ^кг$.
Ответ: Радиус кривизны протона в 42 раза больше, чем радиус кривизны электрона.
Готовые работы на аналогичную тему
Получить выполненную работу либо консультацию спеца по вашему учебному проекту Выяснить цена
Задание: Найдите напряженность электрического поля (E), если протон в скрещенном магнитном и электрическом полях движется прямолинейно. В эти поля он влетел, пройдя ускоряющую разность потенциалов равную U. Поля скрещены под прямым углом. Индукция магнитного поля равна B.
На частичку, по условиям задачи действует сила Лоренца, имеющая две составные части: магнитную и электрическую. 1-ая составляющая магнитная она равна:
$\overrightarrow$ — ориентирована перпендикулярно $\overrightarrowи\ \overrightarrow$. Электрическая составляющая силы Лоренца равна:
Сила $\overrightarrow$- ориентирована по напряженности $\overrightarrow$. Мы помним, что протон имеет положительный заряд. Для того дабы протон двигался прямолинейно нужно, дабы магнитная и электрическая составляющие силы Лоренца уравновешивали друг дружку, другими словами их геометрическая сумма была равна нулю. Изобразим силы, поля и скорость движения протона, выполнив условия их ориентации на рис. 2.