Сила лоренца на заряженную частичку

§ 4. Действие магнитного поля на перемещающуюся заряженную частичку. Сила лоренца

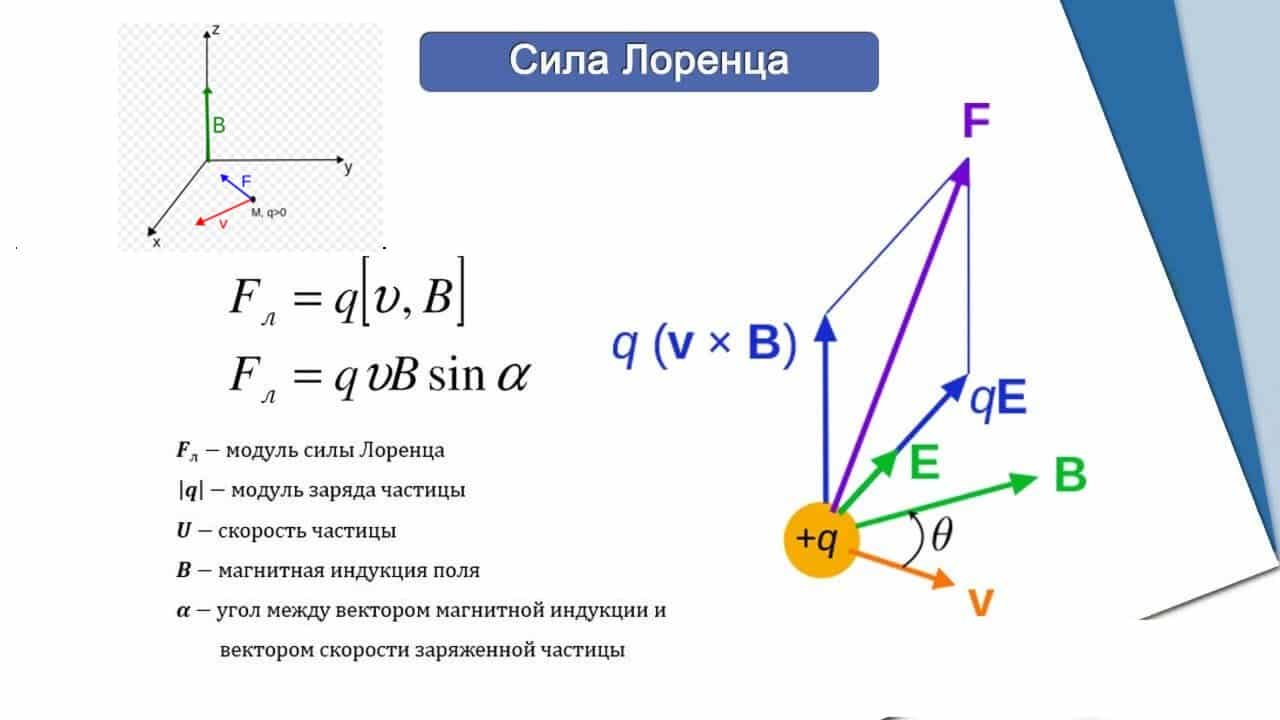
На заряженную частичку, перемещающуюся в магнитном поле, действует сила Лоренца, равная произведению его индукции, заряда частички, ее скорости и синуса угла между направлением скорости и вектором индукции.

Электрический ток представляет собой упорядоченное направленное движение заряженных частиц. Потому действие магнитного поля на проводник с током (сила Ампера) является результатом того, что это поле действует на перемещающиеся снутри проводника заряженные частички. Силу, действующую на заряженную частичку в магнитном поле, именуют силой Лоренца в честь голландского физика Х. Лоренца.

Найдём направление и модуль силы Лоренца F Л при помощи закона Ампера (3.1). Пусть на прямолинейный участок проводника длиной L при силе тока в нем I , находящийся в однородном магнитном поле с индукцией В (рис.4а), действует сила Ампера FА . Если N – число заряженных частиц, упорядоченно перемещающихся на этом участке проводника, то, разумеется, что сила Лоренца, F Л равна:

Найдём N , исходя из того, что сила тока I равна произведению заряда частички q , их концентрации n , скорости их упорядоченного движения v и площади поперечного сечения проводника S :

I = qnvS . (4.2)

Так как , то из (4.2) получаем следующее выражение для N :

подставляя которое в (4.1) и беря во внимание формулу (3.1), получим формулу для FЛ:

Если заряд положительный, то для определения направления силы Лоренца можно воспользоваться правилом левой руки (рис. 4 б ) . На перемещающуюся негативно заряженную частичку сила Лоренца действует в обратном направлении. Сила Лоренца не совершает работы, так как её вектор перпендикулярен вектору скорости движения частички.

Сила Лоренца применяется в электронно-лучевых трубках (ЭЛТ) телевизоров и мониторов, где магнитное поле позволяет отклонять электроны, парящие к экрану ЭЛТ.

Заряженная частичка, влетая в однородном магнитном поле, направленное перпендикулярно вектору ее скорости, начинает умеренно двигаться по окружности радиуса r , а сила Лоренца в данном случае является центростремительной силой (рис. 4в). Радиус окружности движения частиц в магнитном поле можно выяснить из соотношения:

где m – масса заряженной частички. Как видно из (4.5), r находится в зависимости от массы частички, и это применяется в масс-спектрометрах – устройствах, где анализ движения заряженных частиц в магнитном поле позволяет определять их массы. Частички различных символов, влетая в магнитное поле, поворачивают в различные стороны, что даёт возможность найти символ заряда частиц.

Если заряженная частичка движется в магнитном поле так, что вектор скорости v составляет с вектором магнитной индукции B угол , то траекторией движения частички является винтообразная линия (рис. 4г). Потому заряженная частичка, влетая в магнитное поле, продолжает свое движение вдоль линий индукции этого поля. Таким же образом магнитное поле Земли защищает нас и всё живое от потоков заряженных частиц космического места.

Вопросы для повторения:

· Как отыскать направление и модуль силы Лоренца?

· Как действует сила Лоренца на модуль скорости заряженной частички?

· Опишите движение заряженной частички в однородном магнитном поле, если её исходная скорость перпендикулярна линиям магнитной индукции.

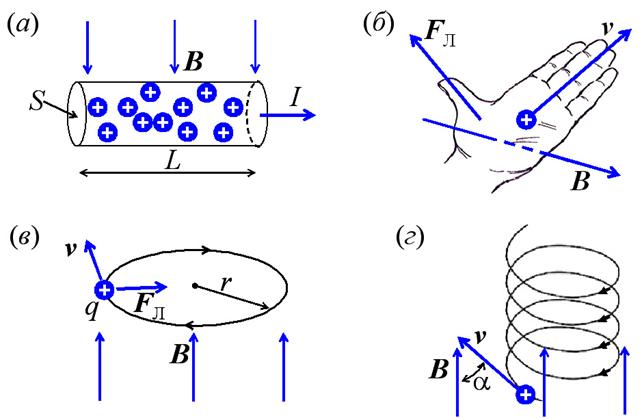
Рис. 4. (а) – к вычислению силы Лоренца; (б) – определение направления силы Лоренца при помощи правила левой руки; движение по окружности (в) и винтообразной полосы (г) заряженной частички в магнитном поле.

Сила Лоренца —>

> > This page is based on a Wikipedia article written by contributors (read/edit).
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

Enjoying Wikiwand?
Give good old Wikipedia a great new look:
Enjoying Wikiwand?

Tell your friends about Wikiwand!

Enjoying Wikiwand?
Give good old Wikipedia a great new look:

• Введение
• Сила Лоренца как определение E и B
• Уравнение
  1. Заряженная частица
  2. Непрерывное распределение заряда
  3. Уравнение в единицах СГС
  4. Частные случаи
• История
• Траектории частиц под действием силы Лоренца
• Значение силы Лоренца
• Сила на токоведущем проводе
• ЭДС
• Сила Лоренца и закон индукции Фарадея
• Сила Лоренца в терминах потенциалов
• Сила Лоренца и аналитическая механика
• Релятивистская форма силы Лоренца
  1. Ковариантная форма силы Лоренца.
  2. Сила Лоренца в алгебре пространства-времени (STA)
  3. Сила Лоренца в общей теории относительности
• Приложения
• Примечания
• Литература
• См. также

Suggest as cover photo

Would you like to suggest this photo as the cover photo for this article?

Thank you for helping!

Your input will affect cover photo selection, along with input from other users.