Силу, действующую на перемещающуюся заряженную частичку со стороны магнитного поля, именуют силой Лоренца в честь величавого нидерландского физика X. Лоренца, основоположника электронной теории строения вещества.
Эту силу можно отыскать при помощи закона Ампера. Она определяется как отношение силы Δ, действующей на участок проводника длиной Δl, к числу N упорядоченно перемещающихся заряженных частиц в этом участке проводника:

Разглядим отрезок узкого прямого провода с током (рис. 4.46). Пусть длина отрезка Δl и площадь поперечного сечения S так малы, что вектор магнитной индукции можно считать постоянным в границах этого отрезка проводника.
Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц n и модулем скорости их упорядоченного движения формулой (2.2.7):

Согласно закону Ампера (4.7.9) сила, действующая на элемент тока а1, в единицах СИ равна:
Подставляя в это выражение значение силы тока (4.9.2), получим:
Векторы Δ и ориентированы идиентично. Потому можно поменять вектор Δ его модулем и вынести из-под знака векторного произведения, сразу заменяя модуль вектора самим вектором и внося его под символ векторного произведения. Тогда
где N = nSΔl — число заряженных частиц в рассматриваемом участке провода.
На каждую заряженную частичку со стороны магнитного поля действует сила Лоренца

Модуль силы Лоренца, согласно определению векторного произведения, равен:

где α — угол между векторами и .
Сила Лоретта перпендикулярна плоскости, содержащей векторы и , и ориентирована для положительно заряженных частиц в сторону поступательного перемещения буравчика при вращении его ручки от вектора к вектору (рис. 4.47). В случае движения негативно заряженных частиц сила Лоренца ориентирована в обратную сторону.
В системе единиц Гаусса сила Лоренца равна:

Электрическое поле действует на заряд q с силой э = q. Поэтому, если есть и электрическое поле и магнитное, то полная сила , действующая на перемещающуюся частичку, равна:

Нередко силой Лоренца именуют полную силу (4.9.6). Тогда силу, определяемую формулой (4.9.3), именуют магнитной частью силы Лоренца.
Наблюдение деяния силы Лоренца
Действие силы Лоренца на перемещающиеся электроны можно следить, поднося электромагнит (либо неизменный магнит) к электронно-лучевой трубке. Меняя ток в электромагните, можно увидеть, что отклонение электронного луча вырастает с повышением модуля вектора магнитной индукции поля. При изменении направления тока в электромагните отклонение луча происходит в обратную сторону.
Зависимость силы Лоренца от угла а между векторами и можно найти, следя смещение электронного луча при изменении угла между осью магнита и осью электронной трубки.
Сила Лоренца не совершает работы
Так как сила Лоренца перпендикулярна скорости частички, то она не совершает работы. Согласно аксиоме о кинетической энергии это значит, что сила Лоренца не меняет кинетическую энергию частички и, поэтому, модуль ее скорости. Под действием силы Лоренца изменяется только направление движения частички.
Появляется естественный вопрос: почему же совершает работу электродвигатель? Ведь проводники обмотки якоря приводятся в движение магнитной силой. Разглядим этот вопрос подробнее.
На рисунке 4.48 изображен один из проводников якоря электродвигателя в магнитном поле. Вектор магнитной индукции поля перпендикулярен плоскости чертежа и ориентирован от нас. По проводнику течет ток сверху вниз. Электроны движутся снизу ввысь со скоростью 1 относительно проводника. Сам проводник движется слева вправо со скоростью 2. Результирующая скорость = 1 + 2 ориентирована под углом к проводнику. Сила Лоренца L перпендикулярна скорости , и ее работа равна нулю. Разложим эту силу на составляющие 2 и 1, направленные вдоль проводника и перпендикулярно ему; L = 1 + 2. При всем этом
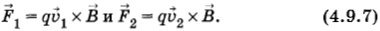
Работа силы Лоренца L в единицу времени (мощность) равна скалярному произведению L • :
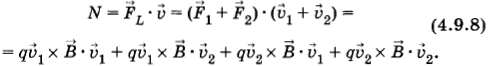
Так как 1 ⊥ 1 х и 2 ⊥ 2 x , то 1-ый и последний члены уравнения (4.9.8) равны нулю. Полная работа силы Лоренца в единицу времени (мощность) равна:
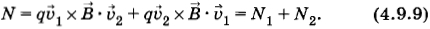
Мощность N1 = q1 х • 2 = 1 • 2 положительна, так как векторы 1 и 2 ориентированы идиентично (см. рис. 4.48).
Так как 1 ⊥ и 1 ⊥ 1 , то

Такую положительную работу совершает в единицу времени магнитное поле по перемещению проводника в целом. Это и есть та работа, которую совершает электродвигатель.
Мощность отрицательна, так как векторы 2 и 1 ориентированы в обратные стороны. Из-за того что 1 ⊥ и 2 ⊥ 2

Эту отрицательную работу совершает в единицу времени магнитное поле по торможению электронов в проводнике.
Положительная работа силы 1 равна по модулю отрицательной работе силы 2, и конкретно поэтому полная работа силы Лоренца равна нулю.
Электроны движутся в проводнике без торможения за счет работы источника. Конкретно источник ЭДС поставляет энергию, нужную для работы электродвигателя.
Сила Лоренца
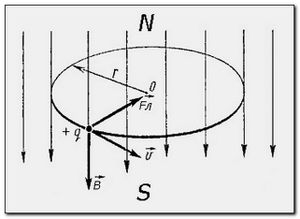
Сила Лоренца (названа в честь голландского физика Хендрика Лоренца, в первый раз который получил верное и полное выражение для этой силы) — сила, действующая на заряженную частичку, перемещающуюся в электромагнитном поле (см. Рис.1). [1]
Силой Лоренца именуют время от времени силу, действующую на перемещающуюся точечную заряженную частичку только со стороны магнитного поля, часто же полную силу — со стороны электромагнитного поля вообщем [2] Она выражается в общем случае для электрического и магнитного полей: F → = q E → + q [ v → × B → ] \vec F = q\vec E+q[\vec v\times\vec B] (в СИ)
Содержание
Со стороны магнитного поля [ править | править код ]
- c c — электродинамическая неизменная
- q q — заряд частички
- v v — скорость частички
- B B — магнитная индукция поля
- α \alpha — угол между вектором скорости и вектором магнитной индукции (см также питч-угол)
- c c — электродинамическая неизменная
- q q — заряд частички
- v v — скорость частички
- B B — магнитная индукция поля
- α \alpha — угол между вектором скорости и вектором магнитной индукции (см также питч-угол)
Полная сила [ править | править код ]
При движении заряженной частички в электромагнитном поле на неё будут действовать и электрическое, и магнитное поле, а полная сила есть сумма сил со стороны первого и второго: F = F e + F m = F = F_e + F_m =\, q E → + q [ v → × B → ] q\vec E+q[\vec v\times\vec B] (в СИ), q E → + q c [ v → × B → ] q\vec E+[\vec v\times\vec B] (в СГС),
- E E — напряжённость электрического поля,
- F m F_m — сила действующая со стороны магнитного поля (сила Лоренца в узеньком смысле),
- F e F_e — сила, действующая со стороны электрического поля,
- другие обозначения — см. параграф выше.
Направление движения частички зависимо от её заряда при векторе магнитной индукции перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей).
Личные случаи (примеры использования) [ править | править код ]
В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частичка будет умеренно двигаться по окружности неизменного радиуса r r . Сила Лоренца в данном случае является центростремительной силой: m v 2 r = | q | v B ⇒ r = m | q | ⋅ v B = |q|vB\Rightarrow r = \cdot (в СИ) m v 2 r = | q | c v B ⇒ r = c m | q | ⋅ v B = <|q|\over c>vB\Rightarrow r = \cdot (в СГС)
Сила Лоренца применяется в телевизионных электронно-лучевых трубках, также в масс-спектрометрии.
Примечания [ править | править код ]
- ↑http://www.oval.ru/enc/41709.html
- ↑ Такая двойственность использования термина «сила Лоренца», разумеется, разъясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна за длительное время до Лоренца, Лоренц же получил общую формулу для деяния и электрического и магнитного полей, отличающуюся от старенькой как раз выражением для магнитного поля. Потому то и другое, полностью разумно, именуют его именованием.
См. также [ править | править код ]
Ссылки [ править | править код ]
При написании этой статьи использовались материалы странички «Сила Лоренца» Российской Википедии.
Сила Лоренца
При определении направления движения электронов при помощи правила левой руки следует учесть, что направление движения электронов обратно техническому направлению тока.
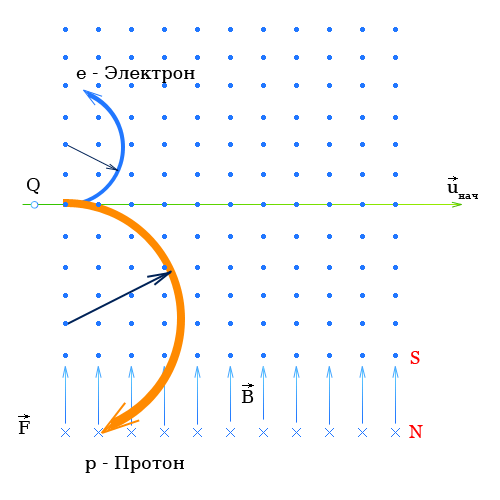
Сила Лоренца действующая на электрон и протон
Величина и направление силы Лоренца определяются соотношением
\[ \vector= e \vector × \vector \]






