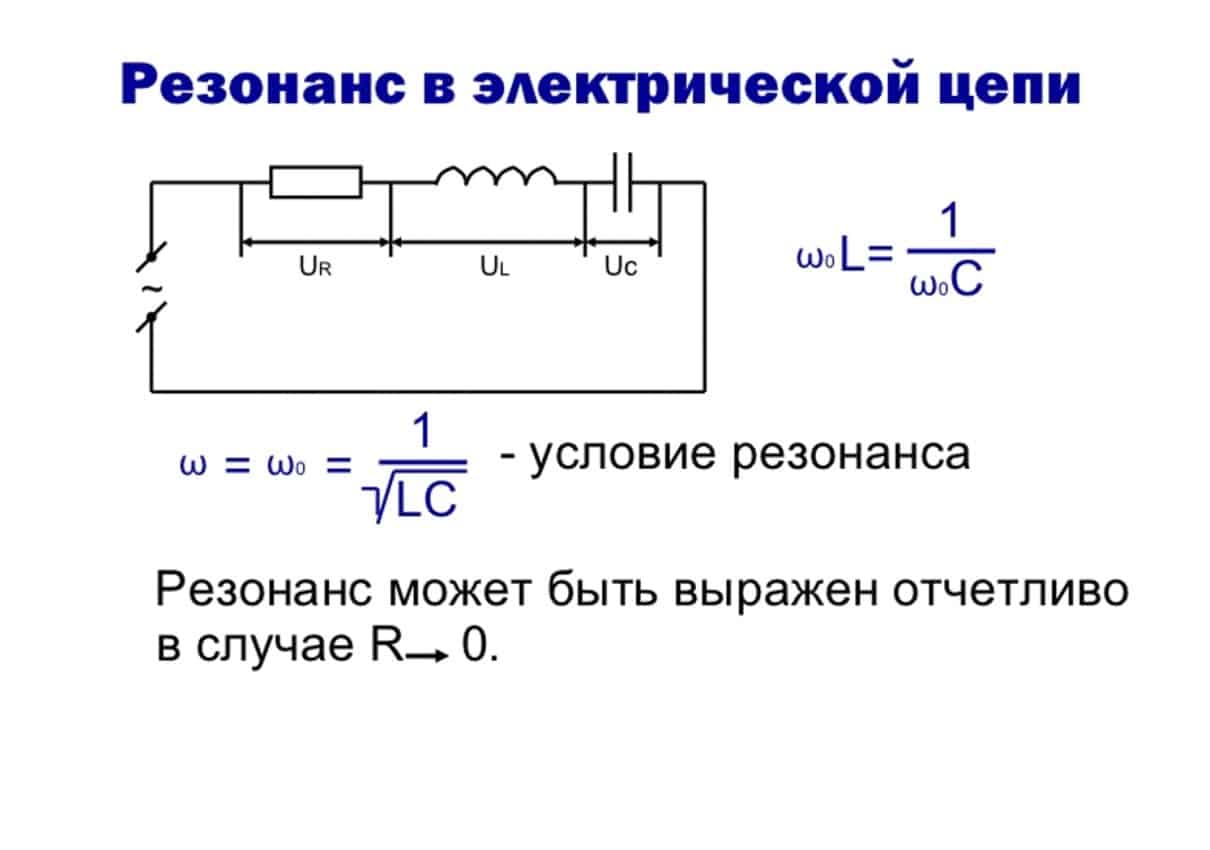
Когда напряжения на индуктивности и емкости UL и UC , взаимно сдвинутые по фазе на 180 , равны по величине, то они стопроцентно компенсируют друг дружку (рис. 18, б). Напряжение, приложенное к цепи, равно напряжению на активном сопротивлении, а ток в цепи совпадает по фазе с напряжением. Этот случай именуется резонансом напряжений.
Условием резонанса напряжений является равенство напряжений на индуктивности и емкости либо равенство индуктивного и емкостного сопротивлений цепи:
xL = xC либо ωL = 1/ωC (1.60)
При резонансе напряжений ток в цепи равен
I = U/√R + 0 = U/R (1.61)
другими словами, цепь в этом случае имеет меньшее вероятное сопротивление, будто бы в нее включено только активное сопротивление R. Ток в цепи при всем этом добивается наибольшего значения.
При резонансе напряжения на реактивных сопротивлениях xL и xC могут приметно превосходить приложенное к цепи напряжение. Если мы возьмем отношение приложенного напряжения к напряжению на индуктивности (либо емкости), то получим
U/ UL = IZ/I xL = Z/ xL либо UL = U xL /R (1.62)
другими словами напряжение на индуктивности будет больше приложенного напряжения в xL /R раз. Это означает, что при резонансе напряжений на отдельных участках цепи могут появиться напряжения, небезопасные для изоляции устройств, включенных в данную цепь. Векторная диаграмма для варианта резонанса напряжений показана на рис. 18 б.
Если в последовательной цепи, содержащей активное сопротивление, индуктивность и емкость изменять величину 1-го из частей цепи (к примеру, емкости) при постоянном приложенном напряжении, то будут изменяться многие величины, характеризующих ток в цепи. Кривые, показывающие как изменяются ток, напряжение, именуются резонансными. Резонансные кривые при изменении емкости показаны на рисунке 20.
Резонанс токов
В отличие от последовательных цепей переменного тока, где ток, протекающий по всем элементам цепи одинаков, в параллельных цепях одинаковым будет напряжение, приложенное к параллельно включенным веткам цепи.
Разглядим параллельное включение емкости и ветки, состоящей из индуктивности и активного сопротивления (рис. 21).
Обе ветки находятся под одним и этим же приложенным напряжением U. Построим векторную диаграмму для этой цепи. В качестве основного вектора выберем вектор приложенного напряжения U (рис. 22).
Потом найдем длину вектора I1 из соотношения
I1 = U/z1 = U/√R1 + xL (1.63)
и отложим этот вектор по отношению к вектору U под углом φ1 , который определяется по формуле
tg φ1 = xL/ R1 (1.64)
Приобретенный таким макаром вектор тока I1 разложим на две составляющие: активную Iа1 = I1 cos φ1 и реактивную Ip1 = I1 sin φ1 (рис. 22).
Величину вектора тока I2 находим из соотношения
I2 = U/ xC = U/(1/ωC) = ωCU (1.65)
и откладываем этот вектор под углом 90 против часовой стрелки относительно вектора приложенного напряжения U.
Общий ток I равен геометрической сумме токов I1 и I2 либо геометрической сумме реактивного тока Ip1 − I2 =IL − IC и активного тока Iа1. длина вектора I равна
I = √(IL − IC ) +( Iа1) (1.66)
Сдвиг по фазе между общим током I и приложенным напряжением U можно найти из соотношения
tgφ =(IL − IC )/ Iа1 (1.67)
Из векторной диаграммы видно, что длина и положение вектора общего тока зависят от соотношения между реактивными токами IL и IC. А именно, при IL > IC общий ток отстает по фазе от приложенного напряжения, при IL < IC ─ опережает его, а при IL = IC ─ совпадает с ним по фазе. Последний случай (IL = IC) именуется резонансом токов. При резонансе токов общий ток равен активной составляющей тока в цепи, другими словами происходящие в цепи процессы таковы, будто бы в ней содержится только активное сопротивление (в данном случае φ = 0 и cos φ = 1). При резонансе общий ток в цепи воспринимает малое значение и становится чисто активным, тогда как реактивные токи в ветвях не равны нулю и обратны по фазе.
Если в параллельной цепи, изображенной на рисунке 21, изменять величину емкости при постоянном приложенном напряжении, то будут изменяться многие величины, характеризующие ток в цепи. Кривые, показывающие как меняются ток, напряжения на участках цепи и сдвиг по фазе между током и напряжением, именуются резонансными.
Резонансные режимы в цепи. Резонанс напряжения, резонанс
Реактивные сопротивления и проводимости отдельных участков цепи могут быть положительными (индуктивные элементы) и отрицательными (емкостные элементы). Потому вероятны такие сочетания этих частей, когда входное реактивное сопротивление либо входная реактивная проводимость всей цепи равны нулю. При всем этом ток и напряжение на входе цепи совпадают по фазе и эквивалентное сопротивление всей цепи является активным. Такие режимы цепи именуются резонансными.
Резонанс напряжений. На рис.2.7 приведена цепь, включающая последовательно соединенные активное сопротивление, индуктивность и емкость. При построении векторных диаграмм этой цепи рассмотрен режим, когда индуктивное и емкостное сопротивления одинаковы по величине (рис.2.10). Напряжения на индуктивности и емкости вполне компенсируют друг дружку. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонанса напряжения.
Ток в резонансном режиме добивается максимума, так как полное сопротивление zцепи имеет малое значение:
Условие появления резонанса: .
Частоту именуют резонансной частотой:
Из (2.46) следует, что режима резонанса можно достигнуть следующими методами:
1) конфигурацией частоты;
2) конфигурацией индуктивности;
3) конфигурацией емкости.
В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут появиться напряжения, существенно превосходящие напряжение на входе цепи, если реактивные сопротивления существенно превосходят активное сопротивление. Напряжение на индуктивности при резонансе равно напряжению на емкости:
Отношение Q именуют добротностью контура.
Добротность указывает, во сколько раз напряжения на реактивных элементах превосходят входное напряжение в резонансном режиме. В радиотехнических цепях добротность составляет несколько сотен. Резонансные характеристики охарактеризовывают также величиной оборотной добротности , именуемой затуханием контура.
Волновое сопротивление контура либо характеристическое сопротивление определяет отношение напряжения на реактивных элементах в резонансном режиме к величине тока:
При резонансе напряжений малые количества энергии, поступающие от источника и компенсирующие энергопотери в активном сопротивлении, достаточны для поддержания незатухающих колебаний относительно огромных количеств энергии магнитного и электрического полей. Покажем, что при резонансе в хоть какой момент времени суммарная энергия магнитного и электрического полей остается неизменной:
Пусть ток в резонансном контуре , тогда напряжение на емкости отстает по фазе от тока на 90 0 .
Суммарная энергия магнитного и электрического полей (2.47) равна:
Если в схеме (рис.2.10) величина ЭДС и характеристики R, L, C неизменны, но изменяется частота , то меняется реактивное сопротивление X и, поэтому, полное сопротивление угол . Зависимости характеристик двухполюсника (реальной и надуманной части входного сопротивления либо входной проводимости) от частоты именуют частотными чертами.
при 3-х соответствующих значениях частоты воспринимает предельные значения, равные нулю, или бесконечности (рис.2.21).
При , при , при имеет место резонанс напряжений и X=0. Аргумент функции, при котором она воспринимает нескончаемое значение, именуется полюсом функции, а аргумент, при котором она воспринимает нулевое значение, именуется нулевым значением. Отметим, что в момент резонанса происходит изменение нрава реактивного сопротивления: при реактивное сопротивление имеет емкостной нрав, а при — индуктивный нрав.
Рис. 2.21
Величина действующего тока в цепи и напряжения на индуктивности и емкости также зависят от конфигурации частоты:
Зависимости действующих значений тока и напряжений на элементах цепи при изменении частоты именуют резонансными кривыми. Резонансные свойства , , приведены на рис.2.23.
Напряжение на емкости при стремится к U, а при стремится к нулевому значению, напряжение на индуктивности при равно нулю, при стремится к U. При резонансной частоте и взаимно компенсируются, ток цепи максимален, напряжение источника приложено к активному сопротивлению.
Рис. 2.22
Из рис. 2.22 видно, что максимум напряжения на индуктивности и максимум напряжения на емкости имеют место при частотах не равных резонансной частоте. Максимум имеет место при частоте наименьшей , а максимум при частоте большей .
В электроэнергетических устройствах воздействие резонанса, обычно, ненужное, так как при резонансе напряжения на индуктивных и емкостных элементах могут существенно превосходить номинальные значения. Такие явления могут появляться при подключении к зажимам синхронного генератора либо трансформатора длинноватой полосы передачи либо кабеля, не замкнутых на приемник нагрузки. Генератор и трансформатор имеют индуктивное сопротивление, а линия либо кабель владеют емкостью и индуктивностью. При отсутствии нагрузки на конце полосы затухание таковой цепи сильно мало и появляются перенапряжения, если частота близка к резонансной.
Явление резонанса напряжений обширно применяется в радиопередающих и радиоприемных устройствах.
Резонанс токов. На рис.2.11 приведена цепь, включающая параллельно соединенные активное сопротивление, безупречная индуктивность и емкость. При построении векторных диаграмм этой цепи рассмотрен режим, когда реактивная проводимость цепи (рис.2.14). При всем этом индуктивный и емкостный токи, направленные в обратные стороны, на сто процентов компенсируют друг дружку. Ток в неразветвленной части схемы совпадает по фазе с напряжением. В электрической цепи наступает режим резонанса токов.
Из условия появления резонанса тока получим формулу для резонансной частоты тока:
Приобретенное выражение для резонансной частоты совпадает с (2.46). Резонанса токов можно достигнуть конфигурацией частоты, конфигурацией индуктивности или емкости.
В режиме резонанса тока полная (входная) проводимость цепи — мала, а полное сопротивление — очень. Ток в неразветвленной части схемы в резонансном режиме имеет малое значение, в отличие от резонанса напряжений, когда ток имеет наибольшее значение. В идеализированном случае при R = 0,
Ток в неразветвленной части цепи I = 0. Такая схема именуется фильтр — пробкой.
При резонансе токов вероятны режимы, когда токи через индуктивность и емкость существенно превосходят ток в неразветвленной части схемы. Превышение токов в реактивных элементах над током в неразветвленной части схемы имеет место при условии
Величина имеет размер проводимости и именуется волновой проводимостью контура.
Добротность контура Q при резонансе токов определяет кратность превышения тока в индуктивности и емкости над током в неразветвленной части схемы :
Величина оборотная добротности является затуханием контура.
Энерго процессы при резонансе токов подобны энергетическим процессам при резонансе напряжений. Малые количества энергии, поступающие от источника и компенсирующие энергопотери в активном сопротивлении, достаточны для поддержания незатухающих колебаний относительно огромных количеств энергии магнитного и электрического полей. Суммарная энергия магнитного и электрического полей при резонансе токов также в хоть какой момент времени остается неизменной.
Частотные свойства проводимостей веток с индуктивностью , с емкостью и входной проводимости приведены на рис. 2.23.
Рис. 2.23
При , при , при имеет место резонанс токов и b=0. В момент резонанса происходит изменение нрава входной проводимости: при входная проводимость имеет индуктивный нрав, а при — емкостной нрав.
Резонансные свойства , , при постоянном входном токе (I = const) и постоянных величинах активного сопротивления, индуктивности и емкости (R = const, L=const, C = const) определяются выражениями
и приведены на рис. 2.24.
При сопротивление индуктивности равно нулю и весь ток протекает через катушку , . При сопротивление конденсатора стремится к нулю и ток проходит только через конденсатор , . При частоте резонанса , токи в индуктивности и конденсаторе взаимно компенсируются, входной ток равен току через активное сопротивление . Максимумы токов через индуктивность и емкость не совпадают с максимумом напряжения при резонансной частоте . Максимум имеет место при частоте наименьшей , а максимум при частоте большей .
Рис. 2.24
В энергетике процесс уменьшения угла сдвига фаз между напряжением на приемнике и током, потребляемым из сети, именуют компенсацией угла сдвига фаз. Входное сопротивление большинства промышленных компаний имеет индуктивный нрав вследствие массового применения асинхронных движков. Для уменьшения величины потребляемого тока за счет компенсации его реактивной составляющей и соответственно утрат электроэнергии в сети, параллельно приемнику энергии включают батареи конденсаторов. Экономически прибыльно подключать конденсаторы на может быть более высочайшее напряжение, так как ток через конденсаторы пропорционален напряжению . Компенсация угла сдвига фаз обычно осуществляется до значения коэффициента мощности cos = 0,9 0,95.
Резонанс в цепях переменного тока
Цель работы. Изучить явление резонанса в цепях переменною тока. Найти резонансные частоты и характеристики цепей для разных типов соединений.
1. Исследование резонанса напряжений в цепях переменного тока
Резонанс напряжений появляется при определенных критериях в цепи переменного тока с последовательно соединенным активным сопротивлением R, соленоидом индуктивностью L и конденсатором емкостью С (рис. 1).
Пусть цепь подключена к источнику синусоидального напряжения U, которое меняется с повторяющейся частотой . По закону Кирхгофа для данной цепи
Дифференциальное уравнение (2) можно решить разными способами, используем для ею решения способ векторных диаграмм.
Эту же задачку можно решить способом векторных диаграмм. Этот способ основан на том, что синусоидально изменяющуюся с течением времени величину (к примеру, графически можно предоставить в виде проекции на вертикальную ось вращающегося вектора, длина которого равна наибольшему (амплитудному) значению . Угловая скорость вращения вектора равна повторяющейся частоте а угол, образованный вектором с горизонтальной осью в исходный момент времени, равен исходной фазе синусоидальной величины (рис. 2).
Пользуясь способом векторных диаграмм, можно алгебраическое сложение моментальных значений синусоидально изменяющихся с течением времени величин одинаковой частоты поменять геометрическим сложением векторов их представляющих. Тогда длина результирующего вектора даст амплитуду результирующей синусоиды, а угол, образованный им с горизонтальной осью — ее исходную фазу.
Может быть для вас будут полезны данные странички:
Построим векторную диаграмму напряжений нашей цепи. Для этого заметим, что если источник в цепи делает синусоидальное напряжение и, изменяющееся с частотой , то ток в цепи будет также синусоидальным с той же частотой. Так как ток в последовательной цепи на всех участках одинаков, то удобнее принять исходную фазу тока равной нулю, а напряжения на участках цепи высчитать при всем этом условии.
где — амплитуда тока. Тогда секундное значение напряжения на активном сопротивлении
т.е. совпадает по фазе с силой тока, где — амплитуда напряжения на активном сопротивлении R.
Секундное значение напряжения на индуктивности
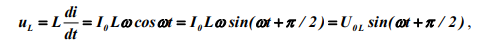
т.е. опережает но фазе силу тока на , где — амплитуда напряжения на катушке индуктивности L.
Секундное значение напряжения на емкости
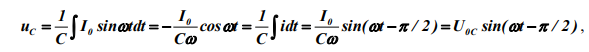
т.е. отстает по фазе от силы тока на , где — амплитуда напряжения на емкости С.
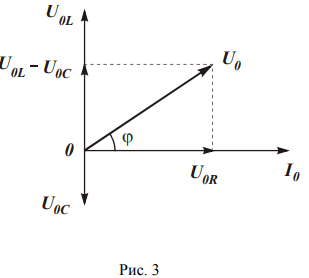
При построении векторной диаграммы вектор тока откладывается горизонтально, так как он одинаков во всех последовательно соединенных элементах цепи R. L и С. Вектора, надлежащие напряжениям, представляются с учетом соответственного сдвига фаз относительно тока (рис. 3).
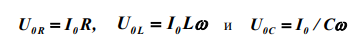
1-ый из них совпадает с направлением вектора, соответственного току, а 2-ой и 3-ий направлены на углы . относительно тока. При сложении этих векторов выходит результирующий вектор, длина которого дает амплитуду приложенного напряжения , а угол — разность фаз напряжения и тока.
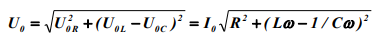
Отсюда получим выражение для силы тока
Величина именуется полным сопротивлением (импедансом) цепи, — индуктивным сопротивлением. — емкостным сопротивлением, а — реактивным сопротивлением цепи. Это выражение представляет собой закон Ома для данной цени, так как связывает амплитудные значения тока и напряжения неизменным коэффициентом Z (при неизменных R, L, С и ).
Сдвиг фаз между током и напряжением также определяется из векторной диаграммы:
Анализ выражений (9) и (10) указывает, что частоту (при неизменных значениях L и С) можно подобрать так, дабы индуктивное и емкостное сопротивления были одинаковыми:
При всем этом реактивное сопротивление X цепи обращается в нуль, полное сопротивление Z мало и равно только активному сопротивлению (Z = R), сила тока и напряжение совпадают по фазе , амплитуда силы тока добивается наибольшей величины:
При этих критериях амплитудные значения напряжений на емкости и индуктивности обратны по фазе и равны по величине
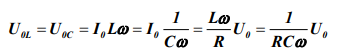
и, потому это явление именуется резонансом напряжений (на индуктивности и емкости), а частота при которой достигается резонанс-резонансной частотой. Она находится из соотношения (11):
Период колебаний тока и напряжений при резонансе
Так как напряжения на индуктивности и емкости меняются в обратных фазах, то суммарное напряжение на участке индуктивность-емкость равно нулю, хотя напряжения на индуктивности и емкости по отдельности могут быть очень значительными и даже большенными, чем напряжение на концах всей цепи.
Вправду, если то, Как видно из выражения (11), , что может быть небезопасным для цепи.
Условие резонанса может быть достигнуто различными методами:
1) подбором частоты при неизменных значениях L и С;
2) подбором индуктивности L при неизменных значениях и С;
3) подбором емкости С при неизменных значениях и L.
Зависимость амплитуды силы тока от частоты графически изображена на рис. 4. Выставленные кривые именуются резонансными. Чем меньше активное сопротивление R, тем круче и острее кривая, а чем больше R, тем кривая более пологая.
Зависимость сдвига фаз от частоты графически изображена на рис. 5, где приведены две кривые для различных значений активного сопротивления R. При частотах сдвиг фаз , т.е. в цени преобладает емкостное сопротивление. При сдвиг фаз , и в цепи преобладает индуктивное сопротивление. При резонансе величина
Все рассмотренные соотношения справедливы и для действующих значений и U, так как последние отличаются от амплитудных только неизменным множителем. К примеру, для гармонически изменяющихся величин
На страничке -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).
Услуги:
Присылайте задания в хоть какое время денька и ночи в ➔
Официальный веб-сайт Брильёновой Натальи Валерьевны педагога кафедры информатики и электроники Екатеринбургского муниципального института.
Все права автора на размещённые материалы сохранены за правообладателями этих материалов. Хоть какое коммерческое и/либо другое внедрение не считая подготовительного ознакомления материалов веб-сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/либо хоть какой другой выгоды.
Веб-сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает продукты и услуги.