Сила Ампера, воздействующая на часть проводника длиной Δ l с некоторой силой тока I , находящийся в магнитном поле B , F = I · B · Δ l · sin α может выражаться через действующие на определенные носители заряда силы.
Пускай заряд носителя обозначается как q , а n является значением концентрации носителей свободного заряда в проводнике. В данном случае произведение n · q · υ · S , в каком S представляет собой площадь поперечного сечения проводника, эквивалентно току, протекающему в проводнике, а υ – это модуль скорости упорядоченного движения носителей в проводнике:
Формула силы Ампера может записываться в следующем виде:
F = q · n · S · Δ l · υ · B · sin α .
Из-за того, что полное число N носителей свободного заряда в проводнике сечением S и длиной Δ l приравнивается произведению n · S · Δ l , действующая на одну заряженную частичку сила приравнивается выражению: F Л = q · υ · B · sin α .
Отысканная сила носит название силы Лоренца. Угол α в приведенной формуле эквивалентен углу между вектором магнитной индукции B → и скоростью ν → .
Направление силы Лоренца, которая повлияет частичку с положительным зарядом, таким же образом, как и направление силы Ампера, находится по правилу буравчика либо же при помощи правила левой руки. Обоюдное размещение векторов ν → , B → и F Л → для частички, несущей положительный заряд, проиллюстрировано на рис. 1 . 18 . 1 .
Набросок 1 . 18 . 1 . Обоюдное размещение векторов ν → , B → и F Л → . Модуль силы Лоренца F Л → численно эквивалентен произведению площади параллелограмма, построенного на векторах ν → и B → и заряда q .
Сила Лоренца ориентирована нормально, другими словами перпендикулярно, векторам ν → и B → .
Сила Лоренца не совершает работы при движении несущей заряд частички в магнитном поле. Этот факт приводит к тому, что модуль вектора скорости в критериях движения частички так же не меняет собственного значения.
Если заряженная частичка движется в однородном магнитном поле под действием силы Лоренца, а ее скорость ν → лежит в плоскости, которая ориентирована нормально по отношению к вектору B → , то частичка будет совершать движение по окружности некоторого радиуса, рассчитывающегося при помощи следующей формулы:
Сила Лоренца в этом случае применяется в качестве центростремительной силы (рис. 1 . 18 . 2 ).
Набросок 1 . 18 . 2 . Радиальное движение заряженной частички в однородном магнитном поле.
Для периода воззвания частички в однородном магнитном поле будет справедливо следующее выражение:
T = 2 π R υ = 2 π m q B .
Данная формула наглядно показывает отсутствие зависимости заряженных частиц данной массы m от скорости υ и радиуса линии движения R .
Использование силы Лоренца
Приведенное снизу соотношение представляет собой формулу угловой скорости движения заряженной частички, происходящего по радиальный линии движения:
ω = υ R = υ q B m υ = q B m .
Оно носит название циклотронной частоты. Данная физическая величина не имеет зависимости от скорости частички, из чего можно прийти к выводу, что и от ее кинетической энергии она не зависит.
Данное событие находит свое использование в циклотронах, а конкретно в ускорителях томных частиц (протонов, ионов).
На рисунке 1 . 18 . 3 приводится принципная схема циклотрона.
Набросок 1 . 18 . 3 . Движение заряженных частиц в вакуумной камере циклотрона.
Дуант – это полый железный полуцилиндр, помещенный в вакуумную камеру между полюсами электромагнита в качестве 1-го из 2-ух ускоряющих D -образного электрода в циклотроне.
К дуантам приложено переменное электрическое напряжение, чья частота эквивалентна циклотронной частоте. Частички, несущие некоторый заряд, инжектируются в центре вакуумной камеры. В промежутке между дуантами они испытывают ускорение, вызываемое электрическим полем. Частички, находящиеся снутри дуантов, в процессе движения по полуокружностям испытывают на для себя действие силы Лоренца. Радиус полуокружностей увеличивается с повышением энергии частиц. Как и во всех других ускорителях, в циклотронах ускорение заряженной частички достигается методом использования электрического поля, а ее удержание на линии движения при помощи магнитного поля. Циклотроны дают возможность ускорять протоны до энергии, приближенной к 20 М э В .
Однородные магнитные поля применяются в почти всех устройствах самых различных типов предназначений. А именно, они отыскали свое использование так именуемых масс-спектрометрах.
Масс-спектрометры – это такие устройства, внедрение которых позволяет нам определять массы заряженных частиц, другими словами ионов либо ядер разных атомов.
Нужна помощь педагога?
Опиши задание — и наши специалисты для тебя посодействуют!
Обрисовать задание
Данные приборы применяются для разделения изотопов (ядер атомов с одинаковым зарядом, но различными массами, например, Ne 20 и Ne 22 ). На рис. 1 . 18 . 4 изображен простая версия масс-спектрометра. Вылетающие из источника S ионы проходят через несколько малых отверстий, которые в совокупы сформировывают узенький пучок. После чего они попадают в селектор скоростей, где частички движутся в скрещенных однородных электрическом, создающимся между пластинами плоского конденсатора, и магнитном, возникающим в зазоре между полюсами электромагнита, полях. Исходная скорость υ → заряженных частиц ориентирована перпендикулярно векторам E → и B → .
Частичка, которая движется в скрещенных магнитном и электрическом полях, испытывает на для себя воздействия электрической силы q E → и магнитной силы Лоренца. В критериях, когда осуществляется E = υ B , данные силы на сто процентов компенсируют воздействие друг дружку. В таком случае частичка будет двигаться умеренно и прямолинейно и, пропархав через конденсатор, пройдет через отверстие в экране. При данных значениях электрического и магнитного полей селектор выделит частички, которые движутся со скоростью υ = E B .
После данных процессов частички с одинаковыми значениями скорости попадают в однородное магнитное поле B → камеры масс-спектрометра. Частички под действием силы Лоренца движутся в камере перпендикулярной магнитному полю плоскости. Их линии движения представляют собой окружности с радиусами R = m υ q B ‘ . В процессе измерения радиусов траекторий при узнаваемых значениях υ и B ‘ , мы имеем возможность найти отношение q m . В случае изотопов, другими словами при условии q 1 = q 2 , масс-спектрометр может поделить частички с различными массами.
При помощи современных масс-спектрометров мы имеем возможность определять массы заряженных частиц с точностью, превосходящей 10 – 4 .
Набросок 1 . 18 . 4 . Селектор скоростей и масс-спектрометр.
Магнитное поле
В случае, когда скорость частички υ → имеет составляющую υ ∥ → вдоль направления магнитного поля, схожая частичка в однородном магнитном поле будет совершать спиралевидное движение. Радиус таковой спирали R находится в зависимости от модуля перпендикулярной магнитному полю составляющей υ ┴ вектор υ → , а шаг спирали p – от модуля продольной составляющей υ ∥ (рис. 1 . 18 . 5 ).
Набросок 1 . 18 . 5 . Движение заряженной частички по спирали в однородном магнитном поле.
Исходя из этого, можно сказать, что линия движения заряженной частички в каком-то смысле «навивается» на полосы магнитной индукции. Данное явление применяется в технике для магнитной теплоизоляции высокотемпературной плазмы — стопроцентно ионизированного газа при температуре порядка 10 6 K . При исследовании управляемых термоядерных реакций вещество в схожем состоянии получают в установках типа «Токамак». Плазма не должна касаться стен камеры. Теплоизоляция достигается методом сотворения магнитного поля специальной конфигурации. На рисунке 1 . 18 . 6 в качестве примера проиллюстрирована траектория перемещения несущей заряд частички в магнитной «бутылке» (либо ловушке).
Набросок 1 . 18 . 6 . Магнитная «бутылка». Заряженные частички не выходят за ее пределы. Нужное магнитное поле может быть сотворено при помощи 2-ух круглых катушек с током.
Такое же явление происходит в магнитном поле Земли, которое защищает все живое от потока несущих заряд частиц из космического места.
Резвые заряженные частички из космоса, по большей степени от Солнца, «перехватываются» магнитным полем Земли, вследствие чего образуются радиационные пояса (рис. 1 . 18 . 7 ), в каких частички, как будто в магнитных ловушках, передвигаются туда и назад по спиралеобразным траекториям между северным и южным магнитными полюсами за толики секунды.
Исключением являются полярные области, в каких часть частиц прорывается в верхние слои атмосферы, что может приводить к появлению таких явлений, как «полярные сияния». Радиационные пояса Земли простираются от расстояний около 500 к м до 10-ов радиусов нашей планетки. Стоит вспомнить, что южный магнитный полюс Земли находится вблизи с северным географическим полюсом на северо-западе Гренландии. Природа земного магнетизма до сего времени не исследована.
Набросок 1 . 18 . 7 . Радиационные пояса Земли. Резвые заряженные частички от Солнца, в главном электроны и протоны, попадают в магнитные ловушки радиационных поясов.
Может быть их вторжение в верхние слои атмосферы, служащее предпосылкой появления «северных сияний».
Сила Лоренца
Действие магнитного поля на перемещающийся заряд
— сила, действующая со стороны магнитного поля на перемещающуюся электрически заряженную частичку.
где q — заряд частички;
V — скорость заряда;
a — угол между вектором скорости заряда и вектором магнитной индукции.
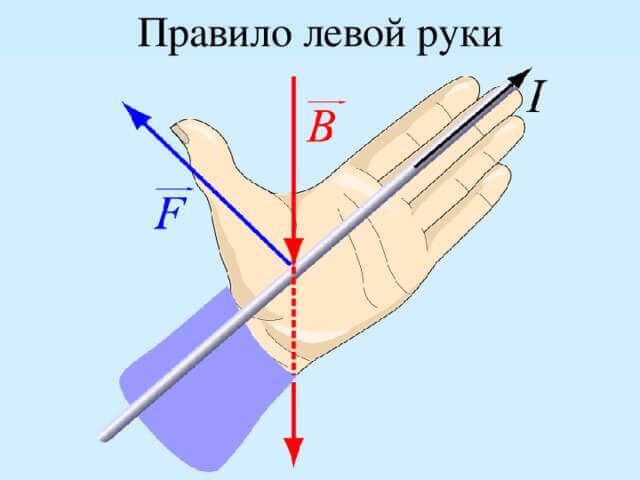
Направление силы Лоренца определяется по правилу левой руки:
Если поставить левую руку так, дабы перпендикулярная скорости составляющая вектора индукции заходила в ладонь, а четыре пальца могли быть размещены по направлению скорости движения положительного заряда (либо против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца:
.
Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.е. не изменяет величину скорости заряда и его кинетическую энергию).
Если заряженная частичка движется параллельно силовым линиям магнитного поля, то Fл = 0 , и заряд в магнитном поле движетсяравномерно и прямолинейно.
Если заряженная частичка движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной:
и делает центростремительное ускорение равное:
В данном случае частичка движется по окружности.
.
Согласно второму закону Ньютона: сила Лоренца равнв произведению массы частички на центростремительное ускорение:
тогда радиус окружности:
а период воззвания заряда в магнитном поле:
Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть итог его деяния на отдельные перемещающиеся заряды. Если внести проводник с током в магнитное поле (фиг.96,а), то мы увидим, что в итоге сложения магнитных полей магнита и проводника произойдет усиление результирующего магнитного поля с одной стороны проводника (на чертеже сверху) и ослабление магнитного поля с другой стороны проводника (на чертеже снизу). В итоге деяния 2-ух магнитных полей произойдет искривление магнитных линий и они, стремясь сократиться, будут выталкивать проводник вниз (фиг. 96, б).
Направление силы, действующей на проводник с током в магнитном поле, можно найти по «правилу левой руки». Если левую руку расположить в магнитном поле так, дабы магнитные полосы, выходящие из северного полюса, вроде бы входили в ладонь, а четыре вытянутых пальца совпадали с направлением тока в проводнике, то большой отогнутый палец руки покажет направление деяния силы. Сила Ампера , действующая на элемент длины проводника, зависит: от величины магнитной индукции В, величины тока в проводнике I, от элемента длины проводника и от синуса угла а между направлением элемента длины проводника и направлением магнитного поля.
Эта зависимость может быть выражена формулой:
Для прямолинейного проводника конечной длины, помещенного перпендикулярно к направлению равномерного магнитного поля, сила, действующая на проводник, будет равна:
Из последней формулы определим размерность магнитной индукции.
Так как размерность силы:
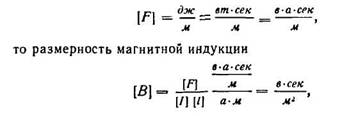
т. е. размерность индукции такая же, какая была получена нами из закона Био и Савара.
Тесла (единица магнитной индукции)
Тесла, единица магнитной индукции Интернациональной системы единиц, равная магнитной индукции, при которой магнитный поток через поперечное сечение площадью 1 м2 равен 1 веберу. Названа по имени Н. Тесла. Обозначения: российское тл, международное Т. 1 тл = 104 гс(гаусс).
Магни?тный моме?нт, магни?тный дипо?льный моме?нт — основная величина, характеризующая магнитные характеристики вещества. Магнитный момент измеряется в А⋅м 2 либо Дж/Тл (СИ), или эрг/Гс (СГС), 1 эрг/Гс = 10 -3 Дж/Тл. Специфичной единицей простого магнитного момента является магнетон Бора. В случае плоского контура с электрическим током магнитный момент рассчитывается как
,
где — сила тока в контуре, — площадь контура, — единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика: если крутить ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика.
Для случайного замкнутого контура магнитный момент находится из:
,
где — радиус-вектор, проведенный из начала координат до элемента длины контура
В общем случае случайного рассредотачивания токов в среде:
,
где — плотность тока в элементе объёма .
Итак, на контур с током в магнитном поле действует крутящий момент. Контур ориентируется в данной точке поля только одним методом. Примем положительное направление нормали за направление магнитного поля в данной точке. Крутящий момент прямо пропорционален величине тока I, площади контура S и синусу угла между направлением магнитного поля и нормали .
тут М – крутящий момент, либо момент силы, – магнитный момент контура (аналогично – электрический момент диполя).
В неоднородном поле ( ) формула справедлива, если размер контура довольно мал (тогда в границах контура поле можно считать приближенно однородным). Поэтому, контур с током как и раньше стремится развернуться так, дабы его магнитный момент был ориентирован вдоль линий вектора .
Но, не считая того, на контур действует результирующая сила (в случае однородного поля и . Эта сила действует на контур с током либо на неизменный магнит с моментом и втягивает их в область более сильного магнитного поля.
Работа по перемещению контура с током в магнитном поле.
Несложно обосновать, что работа по перемещению контура с током в магнитном поле равна , где и — магнитные потоки через площадь контура в конечном и исходном положениях. Эта формула справедлива, если ток в контуре постоянен, т.е. при перемещении контура не учитывается явление электромагнитной индукции.
Формула справедлива и для огромных контуров в сильно неоднородном магнитном поле (при условии I=const).
В конце концов, если контур с током не смещать, а изменять магнитное поле, т.е. изменять магнитный поток через поверхность, охватываемую контуром, от значения до то для этого нужно совершить ту же работу . Эта работа именуется работой конфигурации магнитного потока, связанного с контуром. Потоком вектора магнитной индукции (магнитным потоком) через площадку dS именуется скалярная физическая величина, которая равна
(1)
где Bn=Вcosα — проекция вектора В на направление нормали к площадке dS (α — угол между векторами n и В), dS = dSn — вектор, у которого модуль равен dS, а направление его совпадает с направлением нормали n к площадке. Поток вектора В может быть как положительным, так и отрицательным зависимо от знака cosα (задается выбором положительного направления нормали n). Поток вектора В обычно связывают с контуром, по которому течет ток. В данном случае положительное направление нормали к контуру нами задавалось: оно связывается с током правилом правого винта. Означает, магнитный поток, который создается контуром, через поверхность, ограниченную им самим, всегда положителен.
Поток вектора магнитной индукции ФB через произвольную заданную поверхность S равен
(2)
Для однородного поля и плоской поверхности, которая размещена перпендикулярно вектору В, Bn=B=const и
Из этой формулы задается единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, который проходит через плоскую поверхность площадью 1 м 2 , который размещен перпендикулярно однородному магнитному полю и индукция которого равна 1 Тл (1 Вб=1 Тл•м 2 ).
Аксиома Гаусса для поля В: поток вектора магнитной индукции через всякую замкнутую поверхность равен нулю:
(3)
Эта аксиома является отражением факта, что магнитные заряды отсутствуют, вследствие чего полосы магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.
Поэтому, для потоков векторов В и Е через замкнутую поверхность в вихревом и возможном полях получаются разные формулы.
В качестве примера найдем поток вектора В через соленоид. Магнитная индукция однородного поля снутри соленоида с сердечником с магнитной проницаемостью μ, равна
Магнитный поток через один виток соленоида площадью S равен
а полный магнитный поток, который сцеплен со всеми витками соленоида и именуемый потокосцеплением,