В этой статье вы узнаете, как формулируется закон Ампера, и какого его использование. Также, что же это все-таки за парадокс – сила Ампера.
Электричество – это довольно сложная область физики, состоящая из огромного количества законов и явлений, который сопрвождают движению тока в проводнике.
Сила указывает себя различными методами, вот Для вас обычный пример: если у нас есть два либо больше проводников, по которым проходит электричество, то их тяготение будет ориентировано друг дружке либо напротив.
Понятие силы Ампера
Закон Ампера обрисовывает силу, которая возникает около проводника и соизмерима его длине, силе тока и магнитной индукции, равным образом также косинуса угла между проводником и вектором магнитной индукции. Вследствие этого, выходит такая формула: F=BILcosa. Где F – сила Ампера.
Ни на что не похоже? Сама формула и ее физический смысл подобен силе Лоренца. Разница исключительно в том, что закон Ампера применяется для проводника в магнитном поле, а Лоренца – на заряженные частички.
В дифференциальной форме, уравнение будет смотреться так:
В векторной форме так:
Существует и другая формулировка, которая была открыта Андре Мари Ампером в 1820 году. Она говорит: закон Ампера охарактеризовывает силу, воздействующую на проводник в магнитном поле.
Данная величина, как и другие силы в физике, измеряется в Ньютонах (Н).
Так как закон Ампера подразумевает возникновение какой-нибудь силы, то не взирая ни на что, присутствие 2-ух и больше таких сил вызовет их взаимодействие между собой. Каким же образом?
Самое принципиальное действие в данном законе это, что при содействии параллельных токов, которые движутся в одном направлении, проводники, располагающиеся вблизи, начнут притягиваться. В случае, если токи будут двигаться в различных направлениях они будут отталкиваться.
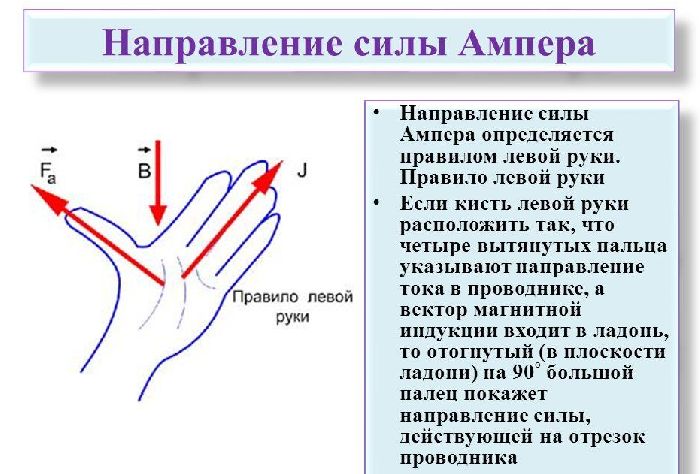
Направление (устремление) силы Ампера
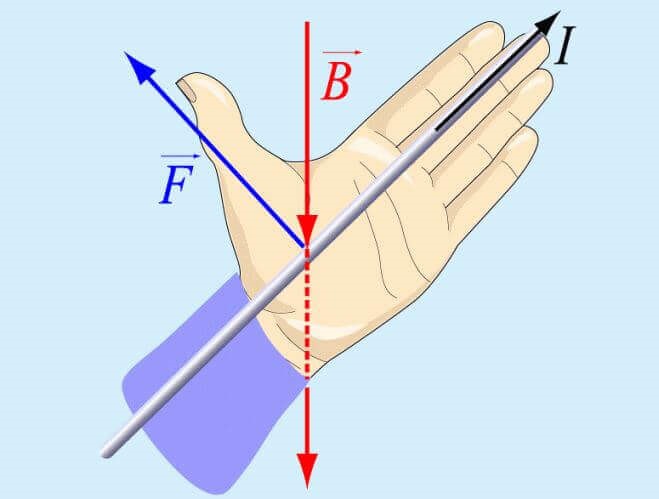
Для определения направления прибегают к правилу левой руки. Для этого Для вас будет нужно расположить раскрытую ладонь левой руки около проводника таким макаром, дабы в нее входили векторы индукции магнитного поля, а четыре открытых пальца демонстрировали направление движение тока.
Вследствие этого, большой палец укажет, куда устремлены силы Ампера и Лоренца.
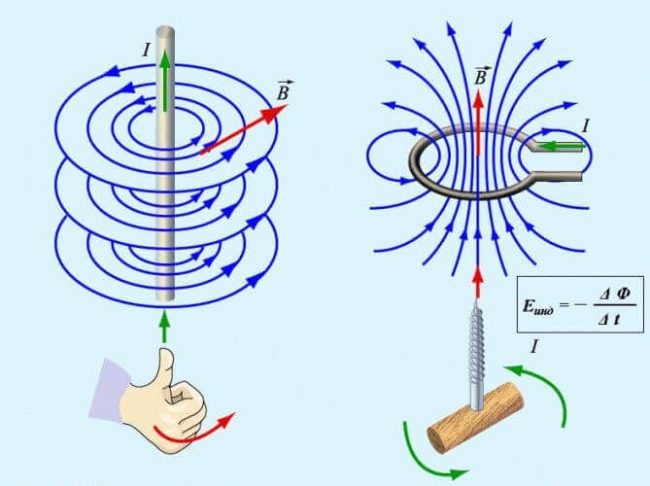
Давайте вспомним, как отыскать направление вектора магнитной индукции… Он находится методом использования правила правой руки: 4-мя пальцами правой руки «обнять» проводник, а большой палец распрямить под углом 90 градусов таким макаром, чтобы он демонстрировал направление тока.
Вследствие этого, четыре согнутых пальца будут изображать круги вокруг токопроводящей нити и указывать, как пробегают полосы магнитного поля.
Использование в жизни
В электротехнике закон Ампера «играет» одну из важнейших «ролей». Давайте обсудим случаи его использования на практике. Электропривод — это база фактически каждого предприятия. Для передвижения либо доведения до действий различных систем, таких как:
- электромобили;
- трамваи;
- троллейбусы;
- автоматические задвижки трубопроводов;
- грузоподъемных устройств;
- электротранспорта (электровозы на ЖД) и других,
используются движки и электромагнитные исполнительные механизмы.
В итоге содействия между обмотками ротора и статора, сила вынуждает мотор крутиться.
Дабы вынудить обмотки крутиться, их или переключают при помощи щеточного узла и коллектора в движках неизменного тока, или применяют переменный ток.
Свое предназначение закон Ампера отыскал также в динамиках и громкоговорителях. В них осуществляется движение мембраны, на которой находится обмотка из медной проволоки в магнитном поле неизменного магнита.
Ее действие просматривается при маленьких замыканиях на линиях электропередач. Там, под воздействием сверхбольших токов, провода и шины начинают изгибаться.
В рельсотроне в момент выстрела раздвигаются рельсы. Это предопределено уже перечисленными выше причинами.
Сила Ампера
Выше представлены выводы из опытов: магнитное поле создается вокруг проводников с током и действует на проводник с током (на перемещающиеся заряды), заставляя проводник передвигаться, если сделаны надлежащие условия.
Закон Ампера был установлен им из опыта, в каком прямолинейный малый участок проводника длиной А/ помещен между полюсами магнита. Проводник так мал, что поле в границах А/ считаем однородным (рис. 3.1.6).
В однородном магнитном поле в хоть какой его точке осуществляется условие


Подробные исследования Ампера привели его к выводу: сила F, которая действует на прямолинейный проводник длиной А/ с током/, находящийся в однородном магнитном поле с индукцией В, определяется выражением:
где а = (у Л /?) — угол между направлением вектора плотности тока ] и
вектором магнитной индукции В; к — коэффициент пропорциональности, значение которого зависит только от выбора единиц измерения применяемых физических величин и равно единице при выражении всех величин в единицах одной и той же системы единиц измерений (не считая системы Гаусса).

Закон Ампера просто обобщить на случай неоднородного магнитного поля и проводника случайной формы. Нескончаемо малый элемент d/ проводника хоть какой формы можно считать прямолинейным, а магнитное поле в области, занятой элементом d/, можно считать однородным (рассматриваем действие поля в данной точке). В общем случае закон Ампера в СИ имеет вид:
Закон Ампера, записанный в виде (3.1.3), не показывает направление силы Ампера cLF, действующей на нескончаемо малый участок проводника d/ с током /. Из опыта сила, действующая на проводник с током, перпендикулярна направлению линий поля В и направлению тока в проводнике, т. е. вектору d/, направление которого совпадает с направлением вектора скорости положительно заряженных носителей.
Направление силы Ампера можно отыскать по правилу левой руки. Если ладонь левой руки расположить так, дабы в нее входили полосы магнитной индукции, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отставленный большой палец укажет направление силы, действующей на проводник со стороны поля (рис. 3.1.7).
В общем случае для отыскания направления вектора dF можно пользоваться правилом определения направления вектора dF, являющегося векторным произведением 2-ух других векторов d/ и В (рис. 3.1.9).
Вектор dF перпендикулярен плоскости, образованной векторами d/ и В , и ориентирован таким макаром, дабы из конца вектора cLF вращение от d/ к В по кратчайшему пути происходило против часовой стрелки.
Используя (3.1.3) и совпадение направления вектора cLF с направлением векторного произведения J^df, i?J, можно записать выражение для силы Ампера в векторном виде:
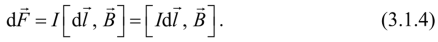
Сила Ампера, действующая на элемент тока в данной точке магнитного поля, пропорциональна векторному произведению элемента тока Ш и вектора индукции поля в данной точке.
Выражение (3.1.3) позволяет найти числовое значение магнитной индукции В .
Из (3.1.3), принимая dF = dFmax, при а = (df Л ^ (т. е. элемент
проводника с током d/ перпендикулярен направлению вектора индукции магнитного поля), получим:

Вектор магнитной индукции численно равен наибольшей силе, действующей со стороны поля на единицу длины проводника, по которому течет ток единичной силы. Таким макаром, магнитная индукция В является силовой чертой магнитного поля, подобно тому, как напряженность Е является силовой чертой электростатического поля.
Единицей измерения магнитной индукции в СИ является тесла (Тл). Согласно (3.1.5) 1 Тл — это магнитная индукция такового однородного магнитного поля, которое действует с силой в 1 Н на каждый метр длины прямолинейного проводника с током в 1 А, размещенного перпендикулярно направлению поля. Таким макаром, можно записать:
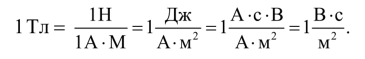
Можно отметить существенную особенность сил электромагнитного взаимодействия по сопоставлению с силами в электростатике, которые являются центральными силами и ориентированы по касательной к силовой полосы электростатического поля в данной точке —
Силы электромагнитного взаимодействия не являются центральными. Они всегда ориентированы перпендикулярно линиям магнитной индукции и проводникам с током, т. е. их абсолютное значение и направление значимым образом находится в зависимости от ориентации в магнитном поле рассматриваемых частей проводников с токами (экспериментально действие силы Ампера можно следить, к примеру, по отклонению проводника, размещенного между полюсами магнита, при пропускании тока по проводнику).
Разглядим действие однородного магнитного поля на проводник случайной формы, обтекаемый током (рис. 3.1.10).
В этом случае вся длина проводника разбивается на простые нескончаемо малые участки d/, любой из которых можно считать прямолинейным элементом тока (ГйГ). На любой из этих участков проводника с током действует простая сила dF, определяемая выражением (3.1.3). В личном случае все простые силы, действующие на любой из частей проводника, могут лежать в одной плоскости, но при переходе от 1-го элемента d/ к другому направление dF может изменяться, и результирующая сила, действующая на весь проводник
с током, F = cLFj + dF2 +. либо F = ^d^.. Тогда при n —> со, запишем,
проводя интегрирование по всей длине проводника:

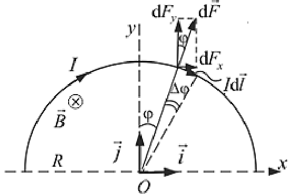
На рисунке (3.1.10.) проводник, имеющий форму полукольца радиусом R, обтекаемый током /, находится в однородном магнитном поле с индукцией В.
Для нахождения результирующей силы (3.1.6) в схожих задачках следует раздельно найти проекции результирующей силы на избранные оси координат (х и у):

Согласно (3.1.3) и рис. 3.1.10, cLF = IBdl, а проекции простой силы на оси х и у соответственно: dFx = dF sin cp, cLF = dFcoscp.
В силу симметрии расположения простых участков относительно оси у получим:
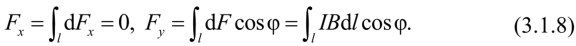
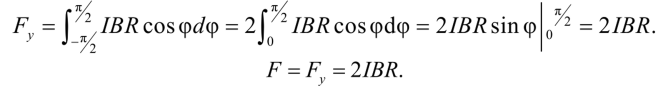
Подставив в (3.1.8) выражение для элемента дуги d/ = Rdy, запишем: