Одним из характеристик, характеризующих поведение электронов в электрической цепи, не считая напряжения и тока, выступает мощность. Она является мерой количества работы, которую можно совершить за единицу времени. Работу обычно ассоциируют с подъёмом веса. Чем больше вес и высота его подъёма, тем больше работы выполнено. Мощность определяет быстроту совершения единицы работы.
Единицы измерения
Мощность автомобилей исчисляют в лошадиных силах – единице измерения, выдуманной изготовителями паровых движков с целью измерения работоспособности собственных агрегатов в обыкновенном источнике энергии тех пор. Мощность автомобиля не гласит, как высоко он может заехать на бугор либо сколько веса он может перевезти, а только указывает, как стремительно он это сделает.
Мощность мотора находится в зависимости от его скорости и крутящего момента выходного вала. Скорость определяют в оборотах за минуту. Крутящий момент – это момент силы мотора, который измерялся сначало в фунт-футах, а на данный момент в ньютон-метрах либо джоулях.
Тракторный мотор в 100 л. с. крутится медлительно, но с огромным вращающим моментом. Мотоциклетный мотор равной мощности крутится стремительно, но с маленьким вращающим моментом. Уравнение расчёта мощности имеет вид:
P = 2π S T / 33000, где S – скорость вращения, об/мин, а T – момент вращения.
Переменными тут являются момент и скорость. По другому говоря, мощность прямо пропорциональна ST: P~ST.
Мощность неизменного тока
В электроцепях мощность находится в многофункциональной зависимости от напряжения и тока. Логично, что она похожа на вышеприведённое уравнение P=IU.
Но здесь P не пропорциональна току, умноженному на напряжение, а приравнивается ему. Исчисляется в ваттах, сокращённо Вт.
Принципиально знать, что ток и напряжение раздельно мощность не определяют, только их совокупа. Напряжение является работой на единицу электрического заряда, а ток – скоростью движения зарядов. Напряжение (эквивалент работы) подобно работе при подъёме веса в противодействие силе гравитации. Ток (эквивалентен скорости) подобен скорости подъёма веса. Их произведение и составляет мощность.
Как тракторный и мотоциклетный моторы, цепь с высочайшим напряжением и маленьким током способна быть одинаковой мощности с цепью низкого напряжения и огромным током. Напряжение и ток вне связи не могут охарактеризовывать мощность электроцепи.
Разомкнутая цепь с напряжением и нулевой силой тока работы не совершает, вне зависимости от высоты напряжения. Ведь, согласно формуле, что угодно, умноженное на 0, даёт 0: P = 0 U = 0. В замкнутой цепи из сверхпроводящего провода с нулевым сопротивлением можно достигнуть тока при напряжении, равном нулю, что также не приведёт к рассеиванию энергии: P = I 0 = 0.
Лошадиные силы и ватты обозначают одно и то же: количество работы, которую можно совершить за единицу времени. Эти единицы взаимосвязаны соотношением
Пример расчёта
Итак, мощность тока электроцепи в ваттах приравнивается произведению напряжения на ток.
Дабы найти, к примеру, мощность нагрузки сопротивлением 3 Ом, в цепи с батареей питания напряжением 12 В, нужно, применив закон Ома, отыскать ток
Умножение приобретенной силы тока на напряжение и даст разыскиваемый итог:
P = I U = 4 А 12 В = 48 Вт
Таким макаром, лампа потребляет 48 Вт.
Что все-таки произойдёт при увеличении напряжения?
При напряжении 24 В и сопротивлении 3 Ом ток
При удвоении напряжения удвоилась и сила тока.
P = IU = 8 А 24 В = 192 Вт
Мощность также возросла, но больше. Почему? Так как это функция произведения напряжения на ток, напряжение и ток возросли в 2 раза, поэтому, мощность возросла в 4 раза. Это можно проверить делением 192 ватт на 48, личное от которого равно 4.
Варианты формулы
Применив алгебру для преобразования формулы, можно взять начальное уравнение и конвертировать его для случаев, когда неизвестен один из характеристик.
Если даны напряжение и сопротивление:
P = (U/R) U либо P = U 2 /R
При известной силе тока и сопротивлении:
P = I (I R) либо P = I 2 R
Исторический факт: отношение между рассеиваемой мощностью и силой тока через сопротивление открыл Джеймс Прескотт Джоуль, а не Георг Симон Ом. Оно было размещено в 1841 г. в виде уравнения P = I 2 R и носит название закона Джоуля–Ленца.
Переменный ток
Закон Ома и Джоуля–Ленца были установлены для неизменного тока, но они справедливы и для моментальных значений изменяющегося тока и напряжения.
Секундное значение P равно произведению моментальных значений силы тока и напряжения с учётом их смещения по фазе на угол φ:
Из уравнения следует, что у моментальной мощности есть неизменная составляющая, и она совершает колебательные движения вокруг среднего значения с частотой, которая в два раза превосходит частоту тока.
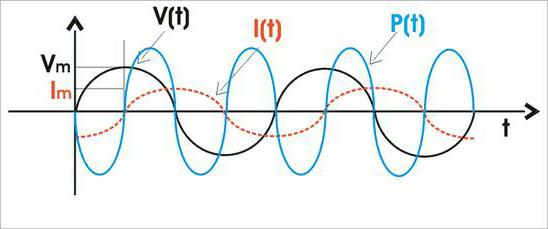
Среднее значение P(t), представляющее практический энтузиазм, равно:
С учётом того, что cos φ=R/Z, где Z=(R 2 + (ωL — 1/ω C) 2 ) 1/2 и Um/Z = Im,
Тут I = Im 2 -1/2 = 0,707 Im – действенное значение силы тока, А.
Аналогично U = Um 2 -1/2 = 0,707 Um – действенное напряжение, В.
Средняя мощность через действенное напряжение и ток определяется
P = U I cos φ, где cos φ – коэффициент мощности.
P в электроцепи перебегает в термическую либо другой вид энергии. Большей активной мощности можно достигнуть при cosφ=1, другими словами при отсутствии сдвига фаз. Она носит название полной мощности
S = U I = Z I 2 = U 2 /Z
Её размерность совпадает с размерностью P, но с целью отличия S измеряется вольт-амперами, ВА.
Степень интенсивности обмена энергией в электроцепи характеризуется реактивной мощностью
Q = U I sinφ = U Ip = Up I = X I 2 = U 2 /X
Она имеет размерность активной и полной, но с целью различения её выражают вольт-амперами реактивными, ВАр.
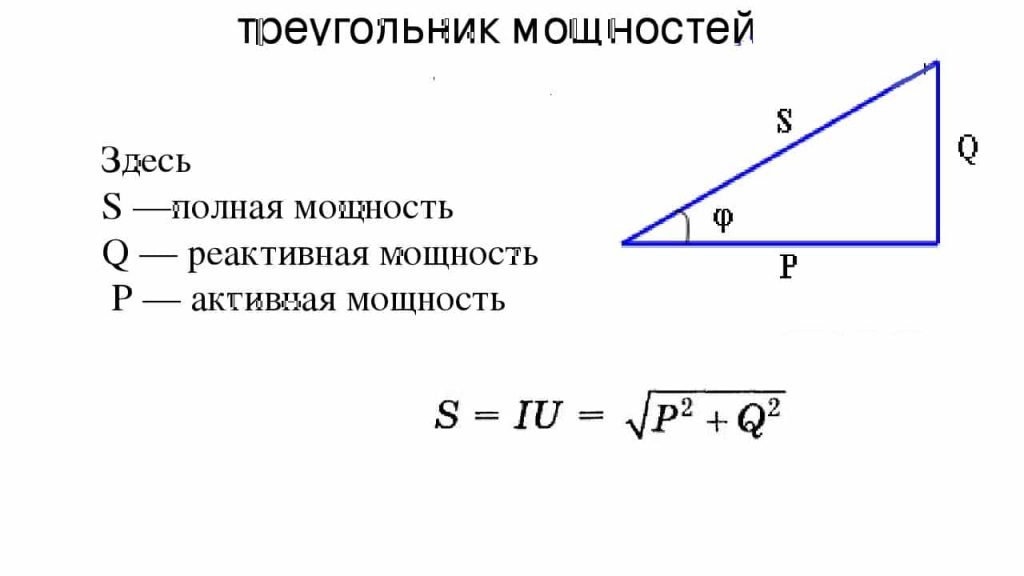
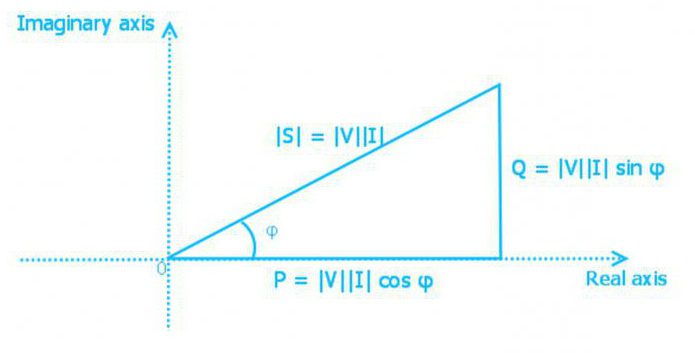
Треугольник мощностей
Мощность активная, реактивная и полная взаимосвязаны выражением
S = (P 2 + Q 2 ) 1/2
Мощность представляют в виде стороны прямоугольного треугольника. Используя законы тригонометрии, можно отыскать длину одной стороны (количество мощности любого типа) по двум известным сторонам либо по длине одной и углу. В таком треугольнике активная мощность является прилежащим катетом, реактивная – противолежащим, а полная мощность – гипотенузой. Угол между катетом активной мощности и гипотенузой равен углу фазы импеданса Z электрической цепи.
Всеохватывающая форма записи этой связи такая:
S = P+jQ = U I cosφ + j U I sinφ= U I e jφ = U I*, где
S – всеохватывающая мощность;
I* – всеохватывающее сопряжённое значение тока.
Вещественная составляющая комплекса – активная, а надуманная – реактивная.
Моментальная полная мощность всегда остаётся неизменной величиной.
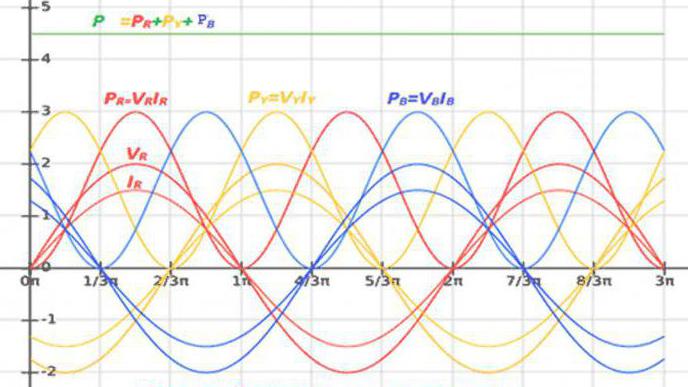
Мощность трёхфазного тока
Нагрузка каждой фазы трёхфазной электроцепи конвертирует энергию либо обменивается ею с источником питания. Вследствие этого P и Q цепи приравниваются суммарной мощности всех фаз:
Активные и реактивные мощности каждой фазы определяются, как в однофазовой цепи.
Полная мощность трёхфазной цепи:
что в всеохватывающей форме имеет вид
Симметричная нагрузка фаз имеет следствием равенство их мощностей. Вот почему мощность тока равна тройной активной и реактивной мощности фазы:
Iф и Uф тут можно поменять их линейными значениями, беря во внимание, что для звезды Uф=Uл; Iф=Iл, а для треугольника Uф=Uл; Iф=Iл3 -1/2 :
Ток несинусоидальной формы
Определение P в цепи несинусоидального тока аналогично её определению в цепи тока синусоидального, так как за период T средняя моментальная мощность
Активная мощность тока определяется суммой P гармонических составляющих, в том числе и неизменной, являющейся гармоникой нулевой частоты.
Реактивная мощность тока схожим образом является результатом сложения Q каждой гармоники.
Полная мощность определяется произведением действенного тока и напряжения:
Полная мощность тока в цепи
Передача энергии w по электрической цепи (к примеру, по полосы электропередачи), рассеяние энергии, другими словами переход электромагнитной энергии в термическую, также и другие виды преобразования энергии характеризуются интенсивностью, с которой протекает процесс, другими словами тем, сколько энергии передается по полосы в единицу времени, сколько энергии рассеивается в единицу времени. Интенсивность передачи либо преобразования энергии именуется мощностью р. Произнесенному соответствует математическое определение:
Выражение для моментального значения мощности в электрических цепях имеет вид:
Приняв исходную фазу напряжения за нуль, а сдвиг фаз между напряжением и током за , получим:
Итак, моментальная мощность имеет постоянную составляющую и гармоническую составляющую, угловая частота которой в 2 раза больше угловой частоты напряжения и тока.
Когда моментальная мощность отрицательна, а это имеет место (см. рис. 1), когда u и i различных символов, т.е. когда направления напряжения и тока в двухполюснике обратны, энергия ворачивается из двухполюсника источнику питания.
Таковой возврат энергии источнику происходит за счет того, что энергия временами запасается в магнитных и электрических полях соответственно индуктивных и емкостных частей, входящих в состав двухполюсника. Энергия, отдаваемая источником двухполюснику в течение времени t равна .
Среднее за период значение моментальной мощности именуется активной мощностью .
Принимая во внимание, что , из (3) получим:
Активная мощность, потребляемая пассивным двухполюсником, не может быть отрицательной (по другому двухполюсник будет генерировать энергию), потому , т.е. на входе пассивного двухполюсника . Случай Р=0, на теоретическом уровне вероятен для двухполюсника, не имеющего активных сопротивлений, а содержащего только безупречные индуктивные и емкостные элементы.
1. Резистор (безупречное активное сопротивление).
Тут напряжение и ток (см. рис. 2) совпадают по фазе , потому мощность всегда положительна, т.е. резистор потребляет активную мощность
2. Катушка индуктивности (безупречная индуктивность)
При безупречной индуктивности ток отстает от напряжения по фазе на . Потому в согласовании с (3) можно записать
.
Участок 1-2: энергия , запасаемая в магнитном поле катушки, наращивается.
Участок 2-3: энергия магнитного поля убывает, ворачиваясь в источник.
3. Конденсатор (безупречная емкость)
Аналогичный нрав имеют процессы и для безупречной емкости. Тут . Потому из (3) вытекает, что . Таким макаром, в катушке индуктивности и конденсаторе активная мощность не потребляется (Р=0), так как в них не происходит необратимого преобразования энергии в другие виды энергии. Тут происходит только циркуляция энергии: электрическая энергия запасается в магнитном поле катушки либо электрическом поле конденсатора в протяжении четверти периода, а в протяжении следующей четверти периода энергия вновь ворачивается в сеть. В силу этого катушку индуктивности и конденсатор именуют реактивными элементами, а их сопротивления ХL и ХС , в отличие от активного сопротивления R резистора, – реактивными.
Интенсивность обмена энергии принято охарактеризовывать большим значением скорости поступления энергии в магнитное поле катушки либо электрическое поле конденсатора, которое именуется реактивной мощностью.
В общем случае выражение для реактивной мощности имеет вид:
Она положительна при отстающем токе (индуктивная нагрузка- ) и отрицательна при опережающем токе (емкостная нагрузка- ). Единицу мощности в применении к измерению реактивной мощности именуют вольт-ампер реактивный (ВАр).
А именно для катушки индуктивности имеем:
Из последнего видно, что реактивная мощность для безупречной катушки индуктивности пропорциональна частоте и наибольшему припасу энергии в катушке. Аналогично можно получить для безупречного конденсатора:
Полная мощность
Кроме понятий активной и реактивной мощностей в электротехнике обширно применяется понятие полной мощности:
Активная, реактивная и полная мощности связаны следующим соотношением:
Отношение активной мощности к полной именуют коэффициентом мощности. Из приведенных выше соотношений видно, что коэффициент мощности равен косинусу угла сдвига между током и напряжением. Итак,
Всеохватывающая мощность
Активную, реактивную и полную мощности можно найти, пользуясь всеохватывающими изображениями напряжения и тока. Пусть , а . Тогда комплекс полной мощности:
где — комплекс, сопряженный с комплексом .
Всеохватывающей мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует (активно-индуктивная нагрузка), для которого имеем:
Использование статических конденсаторов для увеличения cos
Как уже указывалось, реактивная мощность циркулирует между источником и потребителем. Реактивный ток, не совершая полезной работы, приводит к дополнительным потерям в силовом оборудовании и, поэтому, к завышению его установленной мощности. В этой связи понятно рвение к повышению в силовых электрических цепях.
Следует указать, что подавляющее большая часть потребителей (электродвигатели, электрические печи, другие разные устройства и приборы) как нагрузка носит активно-индуктивный нрав.
Если параллельно таковой нагрузке (см. рис. 5), включить конденсатор С, то общий ток , как видно из векторной диаграммы (рис. 6), приближается по фазе к напряжению, т.е. возрастает, а общая величина тока (а поэтому, утраты) миниатюризируется при всепостоянстве активной мощности . На этом основано использование конденсаторов для увеличения .
Какую емкость С необходимо взять, дабы повысить коэффициент мощности от значения до значения ?
Разложим на активную и реактивную составляющие. Ток через конденсатор компенсирует часть реактивной составляющей тока нагрузки :
| ; | (10) |
| ; | (11) |
| . | (12) |
Из (11) и (12) с учетом (10) имеем
но , откуда нужная для увеличения емкость:
Баланс мощностей
Баланс мощностей является следствием закона сохранения энергии и может служить аспектом корректности расчета электрической цепи.
а) Неизменный ток
Для хоть какой цепи неизменного тока осуществляется соотношение:
Это уравнение представляет собой математическую форму записи баланса мощностей: суммарная мощность, генерируемая источниками электроэнергии, равна суммарной мощности, потребляемой в цепи.
Следует указать, что в левой части (14) слагаемые имеют символ “+”, так как активная мощность рассеивается на резисторах. В правой части (14) сумма слагаемых больше нуля, но отдельные члены тут могут иметь символ “-”, что гласит о том, что надлежащие источники работают в режиме потребителей энергии (к примеру, заряд аккума).
б) Переменный ток.
Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей равна сумме всех потребляемых активных мощностей, т.е.
В ТОЭ доказывается (вследствие достаточной громоздкости вывода это подтверждение опустим), что баланс соблюдается и для реактивных мощностей:
| , | (16) |
где символ “+” относится к индуктивным элементам , “-” – к емкостным .
Умножив (16) на “j” и сложив приобретенный итог с (15), придем к аналитическому выражению баланса мощностей в цепях синусоидального тока (без учета обоюдной индуктивности):
- Базы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические базы электротехники: Электрические цепи. Учеб. для учащихся электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- Что такое активная мощность?
- Что такое реактивная мощность, с какими элементами она связана?
- Что такое полная мощность?
- Почему нужно стремиться к увеличению коэффициента мощности ?
- Аспектом чего служит баланс мощностей?
- К источнику с напряжением подключена активно-индуктивная нагрузка, ток в какой . Найти активную, реактивную и полную мощности.
Что такое активная и реактивная мощность переменного электрического тока?
Все мы раз в день сталкиваемся с электроприборами, кажется, без них наша жизнь останавливается. И у каждого из них в технической аннотации указана мощность. Сейчас мы разберемся что все-таки это такое, узнаем виды и методы расчета.
Мощность в цепи переменного электрического тока
Электроприборы, подключаемые к электросети работают в цепи переменного тока, потому мы будем рассматривать мощность конкретно в этих критериях. Но, поначалу, дадим общее определение понятию.
Мощность — физическая величина, отражающая скорость преобразования либо передачи электроэнергии.
В более узеньком смысле, молвят, что электрическая мощность – это отношение работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Если перефразировать данное определение наименее научно, то выходит, что мощность – это некое количество энергии, которое расходуется потребителем за определенный промежуток времени. Самый обычный пример – это рядовая лампа накаливания. Скорость, с которой лампочка превращает потребляемую электроэнергию в тепло и свет, и будет ее мощностью. Соответственно, чем выше вначале этот показатель у лампочки, тем больше она будет потреблять энергии, и тем больше даст света.
Так как в этом случае происходит не только лишь процесс преобразования электроэнергии в некоторую другую (световую, термическую и т.д.), но и процесс колебания электрического и магнитного поля, возникает сдвиг фазы между силой тока и напряжением, и это следует учесть при последующих расчетах.
При расчете мощности в цепи переменного тока принято выделять активную, реактивную и полную составляющие.
Понятие активной мощности
Активная «нужная» мощность — это та часть мощности, которая охарактеризовывает конкретно процесс преобразования электроэнергии в некоторую другую энергию. Обозначается латинской буковкой P и измеряется в ваттах (Вт).
Читайте также: Клеточка Фарадея своими руками
Рассчитывается по формуле: P = U⋅I⋅cosφ,
где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, cos φ – косинус угла сдвига фазы между напряжением и током.
Принципиально! Описанная ранее формула подходит для расчета цепей с напряжением 220В, но, массивные агрегаты обычно применяют сеть с напряжением 380В. В таком случае выражение следует помножить на корень из 3-х либо 1.73
Понятие реактивной мощности
Реактивная «вредная» мощность — это мощность, которая появляется в процессе работы электроприборов с индуктивной либо емкостной нагрузкой, и отражает происходящие электромагнитные колебания. Проще говоря, это энергия, которая перебегает от источника питания к потребителю, а позже ворачивается назад в сеть.
Применять в дело данную составляющую естественно нельзя, не достаточно того, она почти во всем вредит сети питания, поэтому обычно его пробуют восполнить.
Обозначается данная величина латинской буковкой Q.
ЗАПОМНИТЕ! Реактивная мощность измеряется не в обычных ваттах (Вт), а в вольт-амперах реактивных (Вар).
Рассчитывается по формуле:
где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, sinφ – синус угла сдвига фазы между напряжением и током.
Принципиально! При расчете эта величина может быть как положительной, так и отрицательной – зависимо от движения фазы.
Емкостные и индуктивные нагрузки
Основным различием реактивной (емкостной и индуктивной) нагрузки – наличие, фактически, емкости и индуктивности, которые имеют свойство припасать энергию и позднее отдавать ее в сеть.
Индуктивная нагрузка конвертирует энергию электрического тока поначалу в магнитное поле (в течение половины полупериода), а дальше конвертирует энергию магнитного поля в электрический ток и передает в сеть. Примером могут служить асинхронные движки, выпрямители, трансформаторы, электромагниты.
Принципиально! При работе индуктивной нагрузки кривая тока всегда отстает от кривой напряжения на одну вторую полупериода.
Емкостная нагрузка конвертирует энергию электрического тока в электрическое поле, а потом конвертирует энергию приобретенного поля назад в электрический ток. Оба процесса снова же протекают в течение половины полупериода каждый. Примерами являются конденсаторы, батареи, синхронные движки.
Принципиально! Во время работы емкостной нагрузки кривая тока опережает кривую напряжения на одну вторую полупериода.
Коэффициент мощности cosφ
Коэффициент мощности cosφ (читается косинус фи)– это скалярная физическая величина, отражающая эффективность употребления электроэнергии. Проще говоря, коэффициент cosφ указывает наличие реактивной части и величину получаемой активной части относительно всей мощности.
Читайте также: Как выполнить перевод люменов в люксы
Коэффициент cosφ находится через отношение активной электрической мощности к полной электрической мощности.
Направьте внимание! При более четком расчете следует учесть нелинейные преломления синусоиды, но, в обыденных расчетах ими третируют.
Значение данного коэффициента может изменяться от 0 до 1 (если расчет ведется в процентах, то от 0% до 100%). Из расчетной формулы легко осознать, что, чем больше его значение, тем больше активная составляющая, а означает лучше характеристики устройства.
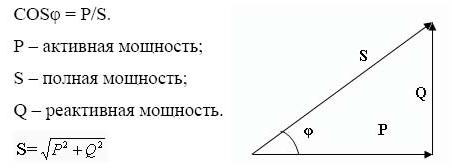
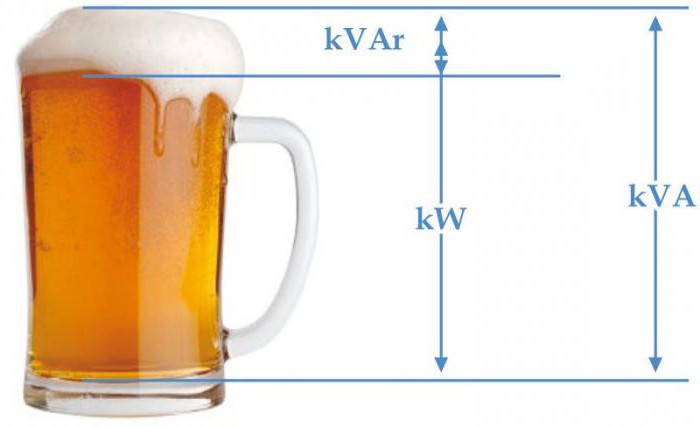
Понятие полной мощности. Треугольник мощностей
Полная мощность – это геометрически вычисляемая величина, равная корню из суммы квадратов активной и реактивной мощностей соответственно. Обозначается латинской буковкой S.
Также высчитать полную мощность можно методом перемножения напряжения и силы тока соответственно.
Принципиально! Полная мощность измеряется в вольт-амперах (ВА).
Треугольник мощностей – это комфортное представление всех ранее обрисованных вычислений и соотношений между активной, реактивной и полной мощностей.
Катеты отражают реактивную и активную составляющие, гипотенуза – полную мощность. Согласно законам геометрии, косинус угла φ равен отношению активной и полной составляющих, другими словами он является коэффициентом мощности.
Как отыскать активную, реактивную и полную мощности. Пример расчета
Все расчеты строятся на обозначенных ранее формулах и треугольнике мощностей. Давайте разглядим задачку, более нередко встречающуюся на практике.
Обычно на электроприёмниках указана активная мощность и значение коэффициента cosφ. Имея эти данные нетрудно высчитать реактивную и полную составляющие.
Для этого разделим активную мощность на коэффициент cosφ и получим произведение тока и напряжения. Это и будет полной мощностью.
Дальше, исходя из треугольника мощностей, найдем реактивную мощность равную квадрату из разности квадратов полной и активной мощностей.
Как определяют cosφ на практике
Значение коэффициента cosφ обычно обозначено на бирках электроприборов, но, если нужно измерить его на практике пользуются спец устройством – фазометром . Также с этой задачей просто управится цифровой ваттметр.
Читайте также: Что такое конденсатор, где применяется и зачем нужен

Если приобретенный коэффициент cosφ довольно низок, то его можно восполнить фактически. Осуществляется это в главном методом включения в цепь дополнительных устройств.
- Если нужно скорректировать реактивную составляющую, то следует включить в цепь реактивный элемент, действующий обратно уже функционирующему устройству. Для компенсации работы асинхронного мотора, для примера индуктивной нагрузки, в параллель врубается конденсатор. Для компенсации синхронного мотора подключается электромагнит.
- Если нужно скорректировать задачи нелинейности в схему вводят пассивный корректор коэффициента cosφ, например, это может быть дроссель с высочайшей индуктивностью, подключаемый последовательно с нагрузкой.
Мощность – это один из важных характеристик электроприборов, потому знать какой она бывает и как рассчитывается, полезно не только лишь школьникам и людям, специализирующимся в области техники, но и каждому из нас.
Как перевести амперы в ватты и назад?
Как перевести амперы в киловаты?
Как высчитать падение напряжения по длине кабеля в электрических сетях
Что такое коэффициент трансформации трансформатора?
Сколько электроэнергии потребляют бытовые приборы, методы вычисления, таблица