Огромное число конденсаторов, которые используют в технике, приближены по типу к плоскому конденсатору. Это конденсатор, который представляет собой две параллельные проводящие плоскости (обкладки), которые делит маленькой промежуток, заполненный диэлектриком. На обкладках сосредоточены равные по модулю и обратные по знаку заряды.
Электрическая емкость плоского конденсатора
Электрическая емкость плоского конденсатора до боли просто выражается через характеристики его частей. Меняя площадь пластинок конденсатора и расстояние между ними просто убедиться, что электрическая емкость плоского конденсатора прямо пропорциональна площади его пластинок (S) и назад пропорциональна расстоянию между ними (d):
Формулу для расчета емкости плоского конденсатора просто получить с помощью теоретических расчетов.
Положим, что расстояние между пластинами конденсатора много меньше, чем их линейные размеры. Тогда краевыми эффектами можно пренебречь, и электрическое поле между обкладками считать однородным. Поле (E), которое делают две нескончаемые плоскости, несущие однообразный по модулю и обратный по знаку заряд, разбитые диэлектриком с диэлектрической проницаемостью , можно найти с помощью формулы:
где — плотность рассредотачивания заряда по поверхности пластинки. Разность потенциалов между рассматриваемыми обкладками конденсатора, находящимися на расстоянии d будет равна:
![\[{\varphi}_1-{\varphi}_2=\int^d_0{Edx=\int^d_0{\frac{\sigma} {\varepsilon {\varepsilon}_0}dx=\frac{\sigma} {\varepsilon {\varepsilon}_0}d}} \qquad (3)\]](/wp-content/uploads/2023/11/ploskij-kondensator-imeet-mezhdu-svoimi-obkladkami_1.png){kind=small}
Подставим правую часть выражения (3) заместо разности потенциалов в (1) беря во внимание, что , имеем:
Энергия поля плоского конденсатора и сила взаимодействия его пластинок
Формула энергии поля плоского конденсатора записывается как:
![\[W_p=\frac{q^2}{2\varepsilon {\varepsilon}_0S}d=\frac{\varepsilon {\varepsilon}_0E^2}{2}Sd=\frac{\varepsilon {\varepsilon}_0E^2}{2}V \qquad (5), \]](/wp-content/uploads/2023/11/ploskij-kondensator-imeet-mezhdu-svoimi-obkladkami_2.png){kind=small}
где – объем конденсатора; E – напряженность поля конденсатора. Формула (5) связывает энергию конденсатора с зарядом на его обкладках и напряженностью поля.
Механическую (пондемоторную) силу, с которой пластинки плоского конденсатора ведут взаимодействие между собой можно отыскать, если применять формулу:
В выражении (6) минус указывает, что пластинки конденсатора притягиваются друг к другу.
Примеры решения задач
| Задание | Чему равно расстояние между пластинами плоского конденсатора, если при разности потенциалов В, заряд на пластинке конденсатора равен Кл? Площадь пластинок , диэлектриком в нем является слюда ( ). |
| Решение | Емкость конденсатора рассчитывается с помощью формулы: |
Из этого выражения получим расстояние между пластинами:
Емкость любого конденсатора определяет формула:
где U – разность потенциалов между обкладками конденсатора. Подставим правую часть выражения (1.3) заместо емкости в формулу (1.2), имеем:
Вычислим расстояние между обкладками ( ):
![\[d=\frac{150\cdot 7\cdot 8,85\cdot {10}^{-12}\cdot {10}^{-2}}{{10}^{-8}}=9,29\cdot {10}^{-3}(m)\]](/wp-content/uploads/2023/11/ploskij-kondensator-imeet-mezhdu-svoimi-obkladkami_3.png){kind=small}
| Задание | Разность потенциалов между пластинами плоского воздушного конденсатора равна В. Площадь пластинок равна , расстояние между ними м. Какова энергия конденсатора и чему она будет равна, если пластинки раздвинуть до расстояния м. Учтите, что источник напряжения при раздвижении пластинок не отключают. |
| Решение | Создадим набросок. |
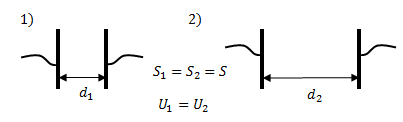
Энергию электрического поля конденсатора можно отыскать с помощью выражения:
Так как конденсатор тонкий, то его электрическую емкость можно вычислить как:
Для первого варианта она будет равна (учтем, что конденсатор воздушный, другими словами =1):
В таком случае энергия конденсатора в первом состоянии:
![\[W_1=\frac{8,85\cdot {10}^{-12}\cdot 2\cdot {10}^{-2}\cdot {(500)}^2}{2\cdot 1,5\cdot {10}^{-3}}=14,8\cdot {10}^{-6}\ (J)\]](/wp-content/uploads/2023/11/ploskij-kondensator-imeet-mezhdu-svoimi-obkladkami_5.png){kind=small}
При манипуляциях с конденсатором при не выключенном источнике напряжения разность потенциалов между обкладками не меняется. Потому:
§ 1.25. Конденсаторы
Конденсатор* представляет собой два проводника, разбитые слоем диэлектрика, толщина которого мала по сопоставлению с размерами проводников. Проводники в данном случае именуют обкладками конденсатора.
Простой тонкий конденсатор состоит из 2-ух одинаковых параллельных пластинок, находящихся на малом расстоянии друг от друга (рис. 1.97). Если заряды пластинок одинаковы по модулю и обратны по знаку, то практически все электрическое поле сосредоточено снутри конденсатора. Полосы напряженности начинаются на положительно заряженной обкладке конденсатора и оканчиваются на негативно заряженной. У сферического конденсатора, состоящего из 2-ух концентрических сфер (рис. 1.98), все поле сосредоточено между обкладками.
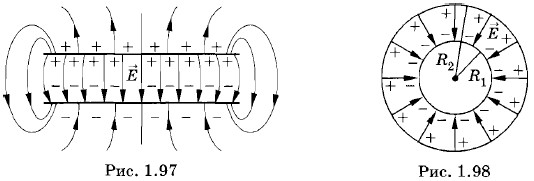
Для зарядки конденсатора необходимо присоединить его обкладки к полюсам источника напряжения, к примеру к полюсам батареи аккумов. Можно также соединить одну обкладку с полюсом батареи, другой полюс которой заземлен, а вторую заземлить. Тогда на заземленной обкладке остается заряд, обратный по знаку и равный по модулю заряду другой обкладки. Таковой же по модулю заряд уйдет в землю.
Под зарядом конденсатора понимают абсолютное значение заряда одной из обкладок.
Разность потенциалов между обкладками конденсатора пропорциональна напряженности поля снутри его. Напряженность поля, сделанного пластинами, в свою очередь пропорциональна заряду пластинок. Потому отношение заряда q 1-го из проводников (на другом находится таковой же по модулю заряд) к разности потенциалов между этим проводником и примыкающим не находится в зависимости от заряда. Оно определяется только геометрическими размерами проводников, их формой и обоюдным расположением, также электрическими качествами окружающей среды (диэлектрической проницаемостью е). Это позволяет ввести понятие электрической емкости 2-ух проводников и, поэтому, емкости конденсатора.
Электроемкостью конденсатора именуют отношение заряда 1-го из проводников к разности потенциалов между этим проводником и примыкающим:
Выражается электрическая емкость конденсатора в тех же единицах, что и емкость уединенных проводников.
Чем меньше напряжение U при сообщении обкладкам конденсатора зарядов +|q| и -|q|, тем больше емкость конденсатора. На обкладках можно накопить огромные заряды, не вызывая пробоя диэлектрика.
Электрические поля окружающих тел практически не попадают вовнутрь конденсатора через его железные обкладки и не оказывают влияние на разность потенциалов между ними. Потому емкость конденсатора фактически не находится в зависимости от наличия поблизости него каких-то тел.
1-ый конденсатор, нареченный лейденской банкой, был сотворен посреди XVII в. Было найдено, что гвоздь, вставленный в стеклянную банку с ртутью, копит большой электрический заряд. Ртуть служила одной обкладкой конденсатора, а ладошки экспериментатора, державшего банку, другой. Потом обе обкладки стали делать из узкой латуни либо станиоля.
Электрическая емкость плоского конденсатора
Получим формулу для вычисления емкости плоского конденсатора. Обозначим площадь каждой его пластинки S, а расстояние между пластинами d. Выразим разность потенциалов U через заряд q. Эта разность потенциалов определяется напряженностью поля Е, которая находится в зависимости от зарядов обкладок конденсатора.
Напряженность поля Е1, сделанного одной из пластинок, рассчитывается по формуле (1.12.4). Напряженности поля положительно и негативно заряженных пластинок равны по модулю и ориентированы снутри конденсатора в одну и ту же сторону. Потому модуль результирующей напряженности равен:
Формула для емкости конденсатора запишется в СИ компактней, если заместо коэффициента k применять его выражение в виде (1.3.5): Тогда, беря во внимание, что поверхностная плотность заряда получим:
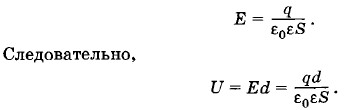
Подставляя это выражение в формулу (1.25.1) и сокращая на q, получим емкость плоского конденсатора в СИ:
В абсолютной системе единиц коэффициент в формуле (1.25.2) k = 1. С учетом этого емкость плоского конденсатора в абсолютной системе единиц равна:
Мы лицезреем, что электроемкость конденсатора находится в зависимости от геометрических причин: площади пластинок и расстояния между ними, также от электрических параметров среды. Она не находится в зависимости от материала проводников: обкладки конденсатора могут быть стальными, медными, дюралевыми и т. д.
Убедимся на опыте в справедливости формулы (1.25.3), приобретенной на теоретическом уровне. Для этого возьмем конденсатор, расстояние между пластинами которого можно изменять, и электрометр с заземленным корпусом (рис. 1.99). Соединим корпус и стержень электрометра с пластинами конденсатора проводниками и зарядим конденсатор. Для этого необходимо коснуться наэлектризованной палочкой пластинки конденсатора, соединенной со стержнем. Электрометр покажет разность потенциалов между пластинами.
Раздвинув пластинки, мы найдем повышение разности потенциалов. Согласно определению электроемкости [см. формулу (1.25.1)] это показывает на ее уменьшение. В согласовании с зависимостью (1.25.3) емкость вправду должна уменьшаться с повышением расстояния между пластинами.
Вставив между обкладками конденсатора пластинку из диэлектрика, к примеру из органического стекла, мы найдем уменьшение разности потенциалов. Поэтому, емкость конденсатора возрастает.
Расстояние между пластинами d может быть очень малым, а площадь S и диэлектрическая проницаемость довольно большенными. Потому при маленьких размерах конденсатор может иметь огромную электрическую емкость. Вобщем, тонкий конденсатор емкостью в 1 Ф был должен бы иметь площадь пластинок S = 100 км 2 при расстоянии между пластинами d = 1 мм.
Задачи на конденсаторы и электроемкость с решениями
Конденсатор – деталька, без которой не обойдется работа ни 1-го электронного устройства. Но до того как разбираться с основами электроники, необходимо научиться решать физические задачи на конденсатор и электроемкость. Конкретно этим мы и займемся в нынешней статье, посвященной подробному разбору решений задач.
Подписывайтесь на наш телеграм: сейчас кроме нужных и увлекательных материалов там можно отыскать скидки и акции на любые работы.
Задачи на конденсаторы и электроемкость с решением
Если вы не понимаете, как решать задачи с конденсаторами, поначалу поглядите теорию и вспомните про памятку по решению задач по физике и полезные формулы.
Задачка №1 на электроемкость батареи конденсаторов
Условие
Тонкий конденсатор емкостью 16 мкФ разрезают на 4 равные части вдоль плоскостей, перпендикулярных обкладкам. Приобретенные конденсаторы соединяют последовательно. Чему равна емкость батaреи конденсаторов?
Решение
Из условия следует, что площадь получившихся конденсаторов в 4 раза меньше, чем у начального. Зная это, можно отыскать емкость каждого приобретенного конденсатора:
Соединяя 4 таких конденсатора последовательно, получаем:
Ответ: 1 мкФ.
Задачка №2 на энергию плоского конденсатора
Условие
Тонкий конденсатор заполнили диэлектриком с диэлектрической проницаемостью, равной 2. Энергия конденсатора без диэлектрика равна 20 мкДж. Чему равна энергия конденсатора после наполнения диэлектриком? Считать, что источник питания отключен от конденсатора.
Решение
Энергия конденсатора до наполнения диэлектриком равна:
После наполнения емкость конденсатора поменяется:
Энергия конденсатора после наполнения:
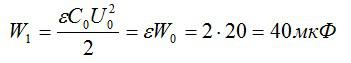
Ответ: 40 мкФ.
Задачка №3 на последовательное и параллельное соединение конденсаторов
Условие
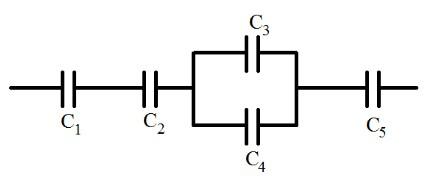
На рисунке изображена батарея конденсаторов. Каждый конденсатор имеет емкость 1 мкФ. Найдите емкость батареи.
Решение
Как лицезреем, часть конденсаторов соединена параллельно, а часть последовательно. Это обычный пример смешанного соединения конденсаторов. Метод решения задач при смешанном соединении конденсаторов сводится к тому, дабы упростить схему и свести все только к параллельному либо последовательному соединению.
Конденсаторы 3 и 4 соединены параллельно. Складывая их емкость, получаем в конечном итоге последовательное соединение 4 конденсаторов: 1, 2, 5 и 3-4. Для параллельного соединения:
Для последовательного соединения:
Ответ: 0,285 мкФ.
Задачка №4 на просвет частички в конденсаторе
Заряд конденсатора равен 0,3 нКл, а емкость – 10 пФ. Какую скорость приобретет электрон, пролетая в конденсаторе от одной пластинки к другой. Исходная скорость электрона равна нулю.
Решение
По закону сохранения энергии, разность кинетических энергий электрона сначала и в конце пути будет равна работе поля по его перемещению. По условию, исходная кинетическая энергия электрона равна 0. Запишем:
С учетом этого, получим:
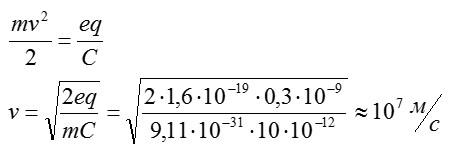
Ответ: 10^7 м/с.
Задачка №5 на вычисление энергии электрического поля конденсатора
Условие
Конденсатор подключен к источнику неизменного напряжения U=1 кВ. Емкость конденсатора равна 5 пФ. Как изменяться заряд на обкладках конденсатора и его энергия, если расстояние между обкладками уменьшить втрое.
Решение
Заряд конденсатора равен:
Изменение заряда будет равно:
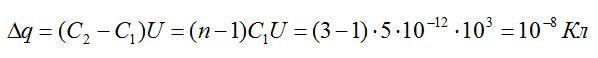
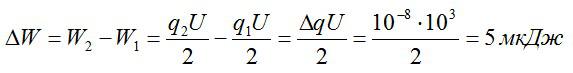
Ответ: 5 мкДж.
Вопросы на тему «Конденсатор и электроемкость»
Вопрос 1. Что такое конденсатор?
Ответ. Конденсатор – устройство, имеющее два полюса и созданное для скопления электрического заряда.
Простой тип конденсатора – тонкий воздушный конденсатор. Он состоит из 2-ух пластинок (обкладок), имеющих различные заряды и разбитых воздухом. Зависимо от диэлектрика, разделяющего обкладки, делят:
- воздушные конденсаторы;
- бумажные конденсаторы;
- слюдяные и другие конденсаторы.
Главная роль конденсатора в электронных устройствах – копить заряд, а позже передавать его далее в цепь.
Вопрос 2. Что такое электроемкость?
Ответ. Электроемкость – скалярная физическая величина, характеризующая способность копить электрический заряд. В системе СИ измеряется в Фарадах.
Вопрос 3. Какие есть методы соединения конденсаторов?
Ответ. Конденсаторы можно соединить последовательно и параллельно.
При параллельном соединении емкость цепи равна сумме емкостей отдельных конденсаторов.
При последовательном соединении величина, оборотная общей емкости, равна сумме оборотных емкостей каждого конденсатора.
Вопрос 4. Что такое колебательный контур?
Ответ. Это простая электрическая цепь, состоящая из конденсатора, катушки индуктивности и источника тока. В колебательном контуре происходят свободные электромагнитные колебания: энергия конденсатора перебегает в энергию катушки, и напротив.
Вопрос 5. Что происходит при выключении источника питания, к которому подключен конденсатор в цепи?
Ответ. В этот момент конденсатор начинает разряжаться, отдавая скопленный заряд другим элементам цепи.
Мы не понасылшке знаем, что от сложных задач на конденсаторы мозги практически плавятся. Если ваш мозг утомился от неизменного решения задач по физике и других заданий, обращайтесь в проф образовательный сервис за консультацией и поддержкой в хоть какое время. У нас есть решение для ваших заморочек с учебой!
Мы поможем сдать на отлично и без пересдач
- Контрольная работа от 1 денька / от 120 р. Выяснить цена
- Дипломная работа от 7 дней / от 9540 р. Выяснить цена
- Курсовая работа 5 дней / от 2160 р. Выяснить цена
- Реферат от 1 денька / от 840 р. Выяснить цена
Иван Колобков, узнаваемый также как Джони. Рекламщик, аналитик и копирайтер компании Zaochnik. Подающий надежды юный писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
