Один из базовых законов, который всегда изучают в курсе физике — это закон Ома . Он относительно обычной, но при всем этом очень важен для корректного осознания. Давайте изучим его в режиме "для чайников".
С осознанием как такого физического явления , обуславливающего возникновение закона Ома, обычно заморочек не появляется. Но вот с вариациями формулировки и записи самого закона, также качествами, связанными с особенностями его использования в различных случаях, трудности часто возникают.
В базе закона Ома лежит некая физическая штука, которая именуется сопротивление .
Понятие сопротивление доходчиво
Электрическое сопротивление — это величина, которая определяет способность проводника пропускать электрический ток . Полезно также освежить познания про электрический ток ( писали в этой статье ).
Представить это проще всего, исходя из строения металлов.
По традиционной теории металл состоит из кристаллической решетки, а между структурными элементами этой решетки путешествуют свободные электроны.
Наружное электрическое поле принуждает их передвигаться и появляется электрический ток, т.е. направленное упорядоченное движение частиц .
Решетка металла мешает им двигаться по собственному объему . Электроны трутся об её узлы и не могут протиснуться. Вот это явление и образует сопротивление. Это "сила", которая мешает перемещению.
Ситуация аналогично ситечку на раковине. Вода проходит, но медлительнее, чем проходила бы без ситечка.
Подобная ситуация находится во всех материалах, правда род и тип частичек может изменяться. Тип строения тоже различный. Но условно можно принять, что всегда структура мешает им двигаться что в дереве, что в металле.
В некоторых телах вообщем таких частичек не будет, там сопротивление нескончаемое (некоторые виды резин, к примеру).
Направьте внимание, что мы не рассматриваем здесь понятие электрического тока и напряжения, т.к. это отдельные темы и если есть недопонимание, непременно напишите об этом в комментах. Правда про электрический ток есть наше видео . Эти вещи необходимо верно осознавать.
Ну и из произнесенного разумеется, что сопротивление будет зависеть от геометрических характеристик проводника (т.е. площадь сечения S, длина l) и типа проводника (который здесь описывается понятием удельное сопротивление и является табличной величиной). Ещё оно находится в зависимости от температуры (чем выше тем больше для большинства тел), но это мы совершенно от самого закона уходим. Для задачек на закон Ома познаний уже полностью довольно.
Формулировка закона Ома
В итоге огромного количества тестов Ом вывел зависимость, которая определяет связь между силой тока в проводнике, напряжением и тем сопротивлением, которое мы обрисовали выше.
Звучит закон так: Cила тока на участке электрической цепи прямо пропорциональна напряжению на концах участка и назад пропорциональна его сопротивлению
Вроде как все слова здесь понятные, если знать все определения. Сопротивление мы разобрали. Сила тока — это, грубо говоря, количество частичек, которое окажется в проводнике. Понятие сила тока тщательно я разбирал в этой статье , непременно прочитайте её.
Напряжение — это "поток", который эти частички несет. Вот как бы всё и увязали.
Если рассматривать цепь, то сопротивление по элементам распределяется согласно их техническим чертам и рассчитывается согласно закону Ома. Т.е. мы не можем утверждать, что на каждом элементе есть однообразное сопротивление.
К примеру, если в цепи с последовательным подключением две лампочки, т омы помним что сила тока во всей цепи при таком соединении однообразная, а вот напряжение на элементах различное. Замеряем его на точках подключения лампочек, записываем и запихиваем в закон Ома. Вот всё и посчитали :).
Закон Ома для участка цепи
Когда закон ома записан в таковой форме, как мы привели выше, то он именуется закон ома для участка цепи .
Почему для участка цепи? Для участка, так как здесь не учитывается сопротивление всей цепи. Можно измерить сопротивление на каждом участке исходя из приведенных черт.
Закон Ома для полной цепи
Полной цепью (в отличие от участка цепи, применительно к которому мы излагали всё выше) именуется цепь с учетом источника тока .
Почему это принципиально?
Конкретно так как если мы представим для себя электрическую цепь условно как систему труб для воды, то участок цепи это будет незамкнутый кусочек трубы, а полная цепь — зацикленная система .
Из примера может показаться, что участок цепи есть незамкнутая в электрическом смысле цепь. Нет, пример приведен не для этого. И там, и там электрическая цепь замкнута.
Просто нам необходимо обозначить, что без учета источника тока и его внутреннего сопротивления (r) цепь не полная, а расчёт не всегда способен учесть все важные свойства.
Ну а внутреннее сопротивление , как вы наверняка додумались — это то сопротивление, которым обладает источник тока. Да, току в цепи трудно перейти и через сам источник! Даже сам источник провоцирует энерго утраты. А вот считать его аналогично расчёту для участка цепи нельзя.
Выходит, что в закон Ома добавится ещё и внутренне сопротивление. И всё! Ничего ужасного.
Формулировка закона Ома для полной цепи мало поменяется. Сейчас у нас слово напряжение заменится словом ЭДС (электродвижущая сила), а слово сопротивление заменится суммой наружного сопротивления цепи и внутреннего сопротивления источника тока. Ну и формула будет такая:
Добавилось понятие электродвижущая сила (ЭДС) , обозначенная в формуле E прописное. Что же это все-таки за зверек?
ЭДС — это, на самом деле дела, и есть напряжение.
Разница в том, что если мы снова сравним напряжение с напором воды в водопроводе, то напряжением будет являться разница напора между 2-мя случайными точками в водопроводе, а ЭДС — это напор на насосе, который качает воду.
При использовании термина ЭДС мы вспоминаем, что у источника есть внутреннее сопротивление, как оно есть и у насоса, который препятствует движению воды через себя самого. Если же мы считали бы конкретно напряжение источника, то мы бы приняли, что система безупречная и источник движению тока сам не препятствует.
Закон Ома в дифференциальной и интегральной формах
При исследовании закона Ома могут выплывать ещё и такие понятия, как закон Ома в дифференциальной и интегральной формах .
Всё это огромные темы, потому мы разглядим их в отдельных статьях.
Здесь отметим только то, что в дифференциальной форме закон Ома применяется для определения характеристик для ничтожно малого участка цепи . Ведь превалирует слово дифференциал либо производная.
В интегральной же форме мы рассматриваем цепь с учетом источника тока либо без него. Аналогично тому, как мы писали выше. Помним, что интеграл по собственной сущности — есть сумма.
Если статья оказалась вам полезной, то непременно поддержите наш проект лайком и подпиской  !
!
Последовательное и параллельное соединения проводников

1. Потребители электроэнергии: электрические лампочки, резисторы и пр. — могут по-разному соединяться вместе в электрической цепи. Существует два главных типа соединения проводников: последовательное и параллельное. При последовательном соединении проводников конец 1-го проводника соединяется с началом другого проводника, а его конец — с началом третьего и т.д. (рис. 85).
Примером последовательного соединения проводников может служить соединение электрических лампочек в ёлочной гирлянде.
При последовательном соединении проводников ток проходит через все лампочки, при всем этом через поперечное сечение каждого проводника в единицу времени проходит однообразный заряд, т.е. заряд не накапливается ни в одной части проводника. Потому при последовательном соединении проводников сила тока в любом участке цепи одинакова: \( I_1=I_2=I \) .
Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений: \( R_1=R_2=R \) . Это следует из того, что при последовательном соединении проводников их общая длина возрастает, она больше, чем длина каждого отдельного проводника, соответственно возрастает и сопротивление проводников.
По закону Ома напряжение на каждом проводнике равно: \( U_1=IR_1 \) , \( U_2=IR_2 \) , а общее напряжение равно \( U=I(R_1+R_2) \) . Так как сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике: \( U=U_1+U_2 \) .
Из приведённых равенств следует, что последовательное соединение проводников применяется в этом случае, если напряжение, на которое рассчитаны потребители электроэнергии, меньше общего напряжения в цепи.
2. Примером параллельного соединения проводников служит соединение потребителей электроэнергии в квартире. Так, электрические лампочки, чайник, утюг и пр. врубаются параллельно.
При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи (А), а вторым концом к другой точке цепи (В) (рис. 86).
Потому вольтметр, присоединенный к этим точкам, покажет напряжение как на проводнике 1, так и на проводнике 2. Таким макаром, напряжение на концах всех параллельно соединённых проводников одно и то же: \( U_1=U_2=U \) .
При параллельном соединении проводников электрическая цепь разветвляется, в этом случае в точке В. Потому часть общего заряда проходит через один проводник, а часть — через другой. Поэтому при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: \( I=I_1+I_2 \) .
В согласовании с законом Ома \( I=\frac \) , \( I_1=\frac \) , \( I_2=\frac \) . Отсюда следует: \( \frac=\frac+\frac \) . Так как \( U_1=U_2=U \) , \( \frac=\frac+\frac \) . Величина, оборотная общему сопротивлению параллельно соединенных проводников, равна сумме величин, оборотных сопротивлению каждого проводника.
При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Вправду, если параллельно соединены два проводника, имеющие однообразное сопротивление \( r \) , то их общее сопротивление равно: \( R=r/2 \) . Это разъясняется тем, что при параллельном соединении проводников вроде бы возрастает площадь их поперечного сечения, соответственно миниатюризируется сопротивление.
Из приведённых формул понятно, почему потребители электроэнергии врубаются параллельно: все они рассчитаны на определённое однообразное напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно высчитать силу тока в каждом из них и соответствие суммарной силы тока максимально допустимой силе тока.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. На рисунке изображёна схема участка электрической цепи АВ. В эту цепь параллельно включены два резистора сопротивлением \( R_1 \) и \( R_2 \) . Напряжения на резисторах соответственно \( U_1 \) и \( U_2 \) .
По какой из формул можно найти напряжение U на участке АВ?
2. На рисунке изображёна схема электрической цепи, содержащая два параллельно включённых резистора сопротивлением \( R_1 \) и \( R_2 \) . Какое из приведённых ниже соотношений справедливо для такового соединения резисторов?
1) \( I=I_1=I_2 \)
2) \( I=I_1+I_2 \)
3) \( U=U_1+U_2 \)
4) \( R=R_1+R_2 \)
3. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением R> и R2. Какое из приведённых ниже соотношений справедливо для такового соединения резисторов?
4. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением \( R_1 \) и \( R_2 \) . Какое из приведённых ниже соотношений справедливо для такового соединения резисторов?
5. На рисунке изображена схема электрической цепи. В эту цепь параллельно включены два одинаковых резистора сопротивлением \( R_1 \) . По какой из формул можно найти общее сопротивление цепи \( R \) ?
6. Общее сопротивление участка цепи, изображённого на рисунке, равно 9 Ом. Сопротивления резисторов \( R_1 \) и \( R_2 \) равны. Чему равно сопротивление каждого резистора?
1) 81 Ом
2) 18 Ом
3) 9 Ом
4) 4,5 Ом
7. Чему равно сопротивление участка цепи, содержащего три последовательно соединенных резистора сопротивлением по 9 Ом каждый?

1) 1/3 Ом
2) 3 Ом
3) 9 Ом
4) 27 Ом
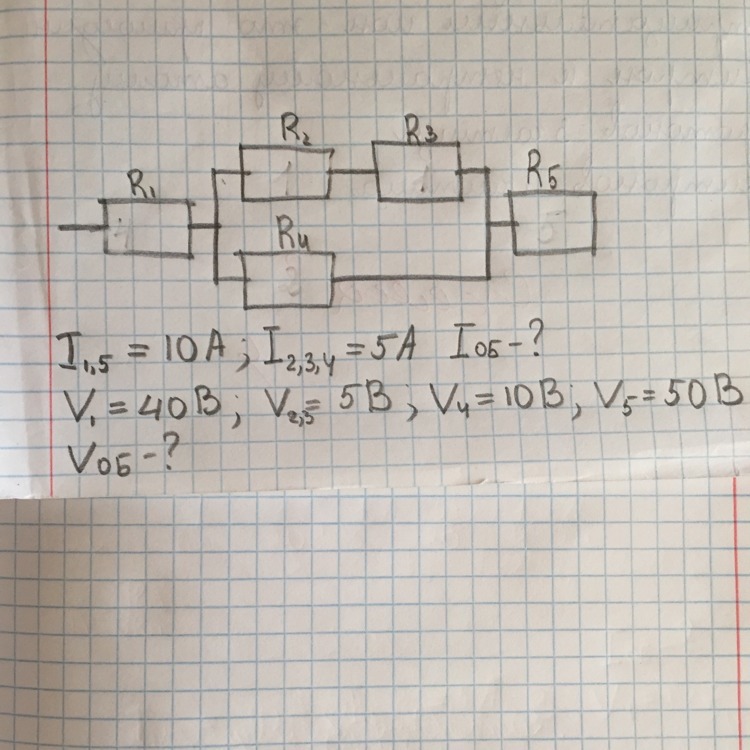
8. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если \( R_1 \) = 1 Ом, \( R_2 \) = 10 Ом, \( R_3 \) = 10 Ом, \( R_4 \) = 5 Ом?
1) 9 Ом
2) 11 Ом
3) 16 Ом
4) 26 Ом
9. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если \( R_1 \) = 1 Ом, \( R_2 \) = 3 Ом, \( R_3 \) = 10 Ом, \( R_4 \) = 10 Ом?
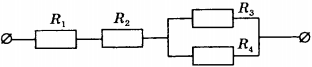
1) 9 Ом
2) 10 Ом
3) 14 Ом
4) 24 Ом
10. Если ползунок реостата (см. схему) переместить на лево, то сила тока
1) в резисторе \( R_1 \) уменьшится, а в резисторе \( R_2 \) возрастет
2) возрастет в обоих резисторах
3) в резисторе \( R_1 \) возрастет, а в резисторе \( R_2 \) уменьшится
4) уменьшится в обоих резисторах
11. На рисунке изображена электрическая цепь, состоящая из источника тока, резистора и реостата. Как меняются при передвижении ползунка реостата на право его сопротивление, сила тока в цепи и напряжение на резисторе 1?
Для каждой физической величины обусловьте соответственный нрав конфигурации. Запишите в таблицу избранные числа для каждой физической величины. Числа в ответе могут повторяться.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) сопротивление реостата 2
Б) сила тока в цепи
B) напряжение на резисторе 1
Нрав Конфигурации
1) возрастает
2) миниатюризируется
3) не меняется
12. Установите соответствие между физическими величинами и правильной электрической схемой для измерения этих величин при последовательном соединении 2-ух резисторов \( R_1 \) и \( R_2 \) . Запишите в таблицу избранные числа под надлежащими знаками. Числа в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) сила тока в резисторе \( R_1 \) и \( R_2 \)
Б) напряжение на резисторе \( R_2 \)
B) общее напряжение на резисторах \( R_1 \) и \( R_2 \)
Часть 2
13. Три резистора соединены, как показано на рисунке. Сопротивления резисторов \( R_1 \) = 10 Ом, \( R_2 \) = 5 Ом, \( R_3 \) = 5 Ом. Каково напряжение на резисторе 1, если амперметр указывает силу тока 2 А?
Сила тока при последовательном соединении
В электрических цепях применяются разные типы соединений. Основными являются последовательные, параллельные и смешанные схемы подключений. В первом случае применяется несколько сопротивлений, соединенных в единую цепочку вереницей. Другими словами, начало 1-го резистора соединяется с концом второго, а начало второго – с концом третьего и т.д., до любого количества сопротивлений. Сила тока при последовательном соединении будет одинаковой во всех точках и на всех участках. Для определения и сопоставления других характеристик электрической цепи, следует рассматривать и другие виды соединений, владеющие своими качествами и чертами.
Последовательное и параллельное соединение сопротивлений
Неважно какая нагрузка обладает сопротивлением, препятствующим свободному течению электрического тока. Его путь проходит от источника тока, через проводники к нагрузке. Для обычного прохождения тока, проводник должен владеть неплохой проводимостью и просто отдавать электроны. Это положение понадобится дальше при рассмотрении вопроса, что такое последовательное соединение.
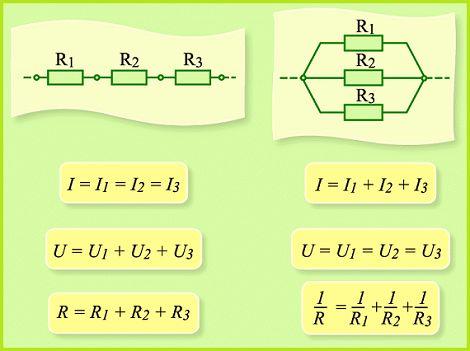
В большинстве электрических цепей используются медные проводники. Любая цепь содержит приемники энергии – нагрузки, владеющие разными сопротивлениями. Характеристики соединения идеальнее всего рассматривать на примере наружной цепи источника тока, состоящей из 3-х резисторов R1, R2, R3. Последовательное соединение подразумевает поочередное включение этих частей в замкнутую цепь. Другими словами начало R1 соединяется с концом R2, а начало R2 – с концом R3 и т.д.. В таковой цепочке может быть хоть какое количество резисторов. Эти знаки применяют в расчетах последовательные и параллельные соединения.
Сила тока на всех участках будет одинаковой: I = I1 = I2 = I3, а общее сопротивление цепи составит сумму сопротивлений всех нагрузок: R = R1 + R2 + R3. Остается только найти, каким будет напряжение при последовательном соединении. В согласовании с законом Ома, напряжение представляет собой силу тока и сопротивления: U = IR. Отсюда следует, что напряжение на источнике тока будет равно сумме напряжений на каждой нагрузке, так как ток всюду однообразный: U = U1 + U2 + U3.
Определение электрического тока
При неизменном значении напряжения, ток при последовательном соединении будет находиться зависимо от сопротивления цепи. Потому при изменении сопротивления хотя-бы на одной из нагрузок, произойдет изменение сопротивления во всей цепи. Не считая того, поменяются ток и напряжение на каждой нагрузке. Главным недочетом последовательного соединения считается прекращение работы всех частей цепи, при выходе из строя даже 1-го из них.
Совсем другие свойства тока, напряжения и сопротивления получаются при использовании параллельного соединения. В данном случае начала и концы нагрузок соединяются в 2-ух общих точках. Происходит типичное разветвление тока, что приводит к понижению общего сопротивления и росту общей проводимости электрической цепи.
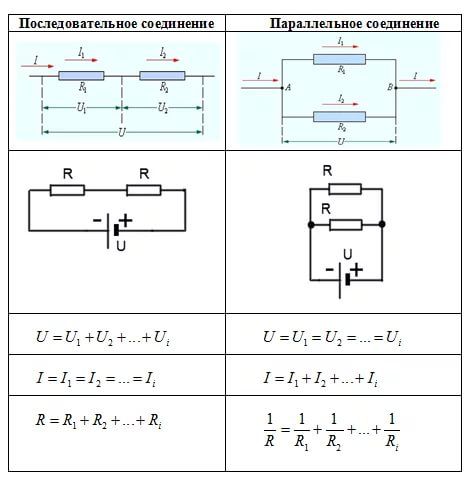
Для того дабы показать эти характеристики, вновь пригодится закон Ома. В этом случае сила тока при параллельном соединении и его формула будет смотреться так: I = U/R. Таким макаром, при параллельном соединении n-го количества одинаковых резисторов, общее сопротивление цепи будет в n раз меньше любого из них: Rобщ = R/n. Это показывает на назад пропорциональное рассредотачивание токов в нагрузках по отношению к сопротивлениям этих нагрузок. Другими словами, при увеличении параллельно включенных сопротивлений, сила тока в них будет пропорционально уменьшаться. В виде формул все свойства показываются следующим образом: сила тока – I = I1 + I2 + I3, напряжение – U = U1 = U2 = U3, сопротивление – 1/R = 1/R1 + 1/R2 + 1/R3.
При постоянном значении напряжения между элементами, токи в этих резисторах не имеют зависимости друг от друга. Если один либо несколько резисторов будут выключены из цепи, это никак не воздействует на работу других устройств, остающихся включенными. Данный фактор является главным преимуществом параллельного соединения электроприборов.
Шаговое напряжение
В схемах обычно не применяется только последовательное соединение и параллельное соединение сопротивлений, они используются в комбинированном виде, известном как смешанное соединение. Для вычисления черт таких цепей используются формулы обоих вариантов. Все расчеты разбиваются на несколько шагов, когда сначала определяются характеристики отдельных участков, после этого они складываются и выходит общий итог.
Законы последовательного и параллельного соединения проводников
Главным законом, используемым при расчетах разных видов соединений, является закон Ома. Его главным положением является наличие на участке цепи силы тока, прямо пропорциональной напряжению и назад пропорциональной сопротивлению на данном участке. В виде формулы этот закон смотрится так: I = U/R. Он служит основой для проведения расчетов электрических цепей, соединяемых последовательно либо параллельно. Порядок вычислений и зависимость всех характеристик от закона Ома наглядно показаны на рисунке. Отсюда выводится и формула последовательного соединения.

Более сложные вычисления с ролью других величин требуют использования правила Кирхгофа. Его основное положение состоит в том, что несколько последовательно соединенных источников тока, будут владеть электродвижущей силой (ЭДС), составляющей алгебраическую сумму ЭДС каждого из них. Общее сопротивление этих батарей будет состоять из суммы сопротивлений каждой батареи. Если осуществляется параллельное подключение n-го количества источников с равными ЭДС и внутренними сопротивлениями, то общая сумма ЭДС будет равно ЭДС на любом из источников. Значение внутреннего сопротивления составит rв = r/n. Эти положения животрепещущи не только лишь для источников тока, но и для проводников, в том числе и формулы параллельное соединение проводников.
В этом случае, когда ЭДС источников будет иметь различное значение, для расчетов силы тока на разных участках цепи используются дополнительные правила Кирхгофа.