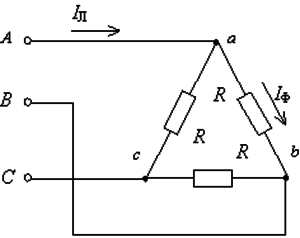
Есть разные методы соединения обмоток генератора с нагрузкой. Самым неэкономичным методом явилось бы соединение каждой обмотки генератора с нагрузкой 2-мя проводами, на что потребовалось бы 6 соединительных проводов. В целях экономии обмотки трехфазного генератора соединяют в звезду либо треугольник. При всем этом число соединительных проводов от генератора к нагрузке миниатюризируется с 6 до 3-х либо до 4.
На электрической схеме трехфазный генератор принято изображать в виде 3-х обмоток, расположенных друг к другу под углом 120°. При соединении звездой одноименные зажимы (к примеру, концы х, у, z) 3-х обмоток объединяют в одну точку (рис. 6.5), которую именуют нулевой точкой генератора 0. Обмотки генератора обозначают знаками А, В, С; буковкы ставят: А —у начала первой, В — у начала 2-ой и С — у начала третьей фазы.
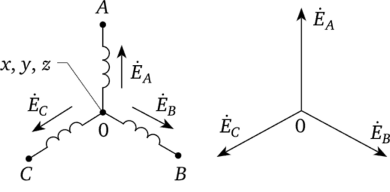
При соединении обмоток генератора треугольником (рис. 6.6) конец первой обмотки генератора соединяют с началом 2-ой, конец 2-ой — с началом третьей, конец третьей — с началом первой. Геометрическая сумма ЭДС в замкнутом треугольнике равна нулю. Потому если к зажимам А, В, С не присоединена нагрузка, то по обмоткам генератора не будет протекать ток.
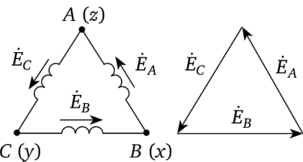
Обратим внимание на то, что размещение звезды либо треугольника векторов фазовых ЭДС на всеохватывающей плоскости не следует связывать с расположением в пространстве осей 3-х обмоток генератора.
5 простых методов соединения трехфазного генератора с трехфазной нагрузкой изображены на рис. 6.7 — 6.10.
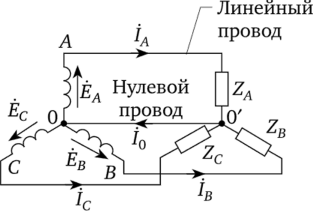
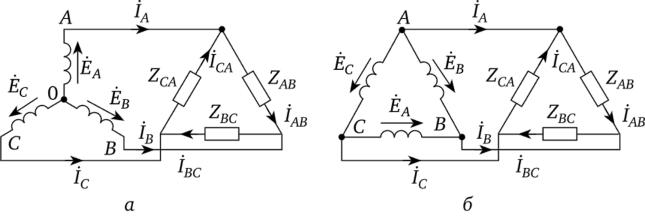
Точку, в какой объединены три конца трехфазной нагрузки при соединении ее звездой, именуют нулевой точкой нагрузки и обозначают О’. Нулевым проводом именуют провод, соединяющий нулевые точки генератора и нагрузки. Ток нулевого провода назовем /0. Положительное направление тока возьмем от точки 0′ к точке 0.
Провода, соединяющие точки А, В, С генератора с нагрузкой, именуют линейными.
Схему на рис. 6.7 именуют «звезда — звезда с нулевым проводом»; на рис. 6.8 — «звезда — звезда без нулевого провода»; на рис. 6.9, а — «звезда — треугольник»; на рис. 6.9, б — «треугольник — треугольник»; на рис. 6.10 — «треугольник — звезда».
Текущие по линейным проводам токи именуют линейными; их обозначают iA, iB, ic. Условимся за положительное направление токов принимать направление от генератора к нагрузке. Модули линейных токов нередко обозначают /л (не указав никакого дополнительного индекса), в особенности тогда, когда все линейные токи по модулю одинаковы.
Напряжение между линейными проводами именуют линейным и нередко пичкают 2-мя индексами, к примеру UM (линейное напряжение между точками А и В); модуль линейного напряжения обозначают
Каждую из 3-х обмоток генератора именуют фазой генератора; каждую из 3-х нагрузок — фазой нагрузки; протекающие по ним токи — фазовыми токами генератора Iф либо, соответственно, нагрузки, а напряжения на них — фазовыми напряжениями (Нф).
Пример решения задачи на расчет трехфазной цепи соединенной звездой.
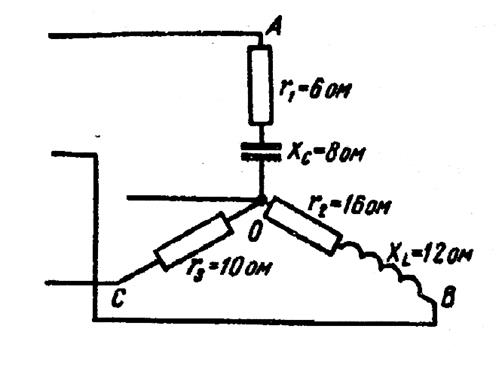
Задачка: В каждую фазу трехфазной четырехпроводной сети включили сопротивления так, как показано на рис. 6. Величины сопротивлений даны на рисунке. Линейное напряжение сети U=380B. Найти: линейные токи, углы сдвига фаз, ток в нулевом проводе, активную, реактивную и полную мощности 3-х фаз. Выстроить в масштабе векторную диаграмму.
Решение. 1. Полные сопротивления фаз:
2. Углы сдвига фаз:
3. Фазное напряжение
4. Линейные (фазные) токи:
5. Активная мощность потребляется только активными сопротивлениями. Потому активная мощность 3-х фаз
6. Реактивная мощность потребляется только реактивными сопротивлениями. Потому реактивная мощность 3-х фаз
Символ «минус» указывает, что реактивная мощность системы носит емкостный нрав.
7. Полная мощность 3-х фаз:
8. Построение векторной диаграммы начинаем с векторов фазных напряжений.
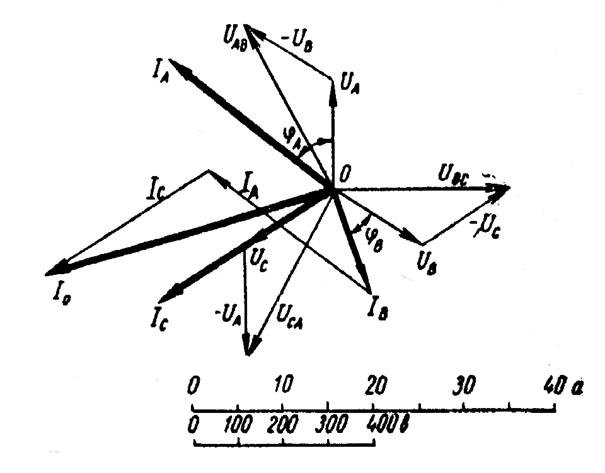
Рис. 7.
Из точки О (рис. 7) в принятом масштабе напряжений проводим три вектора фазных напряжений , и , углы между которыми составляют 120°. Потом строим векторы линейных напряжений , и , согласно уравнениям:
Черточки над знаками демонстрируют, что векторы должны вычитаться и складываться геометрически. К примеру, для построения линейного напряжения к вектору необходимо геометрически прибавить оборотный по направлению вектор .
Под углом φА=53° в сторону опережения вектора фазного напряжения откладываем в принятом масштабе токов вектор тока ; под углом φВ=37° в сторону отставания от вектора фазного напряжения откладываем вектор тока .
Вектор тока совпадает по направлению с вектором фазного напряжения так как φС=0.
Для определения тока в_нулевом проводе I0 складываем геометрически векторы токов , и . Из векторной диаграммы, пользуясь масштабом для токов, находим ток I0=34A.
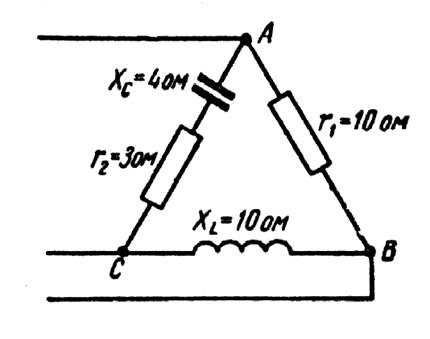
Пример 2:В каждую фазу трехфазной сети включили сопротивления так, как показано на рис. 8. Величины сопротивлений даны на рисунке3. Линейное напряжение сети U =220B.
Рис. 8.
Найти: фазные и линейные токи, углы сдвига фаз, активную, реактивную и полную мощности 3-х фаз. Выстроить в масштабе векторную диаграмму.
Решение 1. Полные сопротивления фаз:
2. Углы сдвига фаз:
4. Активная мощность потребляется только активными сопротивлениями. Потому активная мощность 3-х фаз
5. Реактивная мощность потребляется только реактивными сопротивлениями. Потому реактивная мощность 3-х фаз
6. Полная мощность 3-х фаз
7. Для определения линейных токов строим векторную диаграмму (рис. 4). Построение _начинаем с векторов фазных (линейных) напряжений , и .
Вектор тока совпадает с вектором фазного напряжения , так как φАВ=0.
Вектор тока отстает от вектора на угол φВС =90°, а вектор тока опережает вектор на угол φВС =53° .
Линейные токи , и на диаграмме равны геометрической разности соответственных фазных токов. К примеру, , т.е. ток в линейном проводе А равен геометрической сумме вектора фазного тока и оборотного вектора фазного тока .
Из векторной диаграммы графически, пользуясь масштабом, определяем линейные токи: IA=66A; IB=43A; IC=25A.