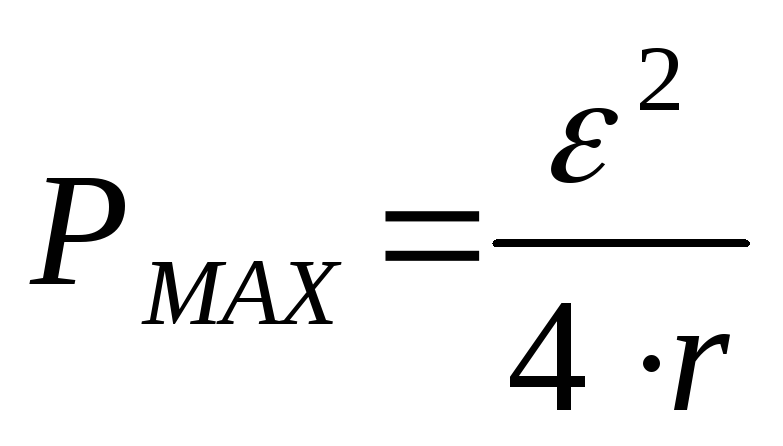Напряжение на внутреннем сопротивлении формула

если б

Основной чертой двухполюсника является его импеданс. Но впрямую охарактеризовывать двухполюсник импедансом не всегда может быть. Дело в том, что термин импеданс примени́м только для чисто пассивных частей, другими словами не содержащих внутри себя источников энергии. Если двухполюсник содержит внутри себя источник энергии, то понятие импеданса к нему просто не применимо, так как закон Ома в формулировке U=Ir не осуществляется [1] .

Таким макаром, имеет смысл гласить о внутреннем сопротивлении только для двухполюсников, содержащих источники (другими словами [2] , то внутреннее сопротивление для такового двухполюсника значит то же самое, что и импеданс.

Схожие определения

Если в какой-нибудь системе можно выделить вход и/либо выход, то нередко употребляются следующие определения:

Входное сопротивление — внутреннее сопротивление двухполюсника, которым является вход системы.
Выходное сопротивление — внутреннее сопротивление двухполюсника, которым является выход системы.

Физические принципы

Невзирая на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (при этом мощности, отдаваемой этим источником в нагрузку, превысить определенный предел. Более обычный пример такового эффекта — ненулевое сопротивление проводников электрической цепи. Но, обычно, больший вклад в ограничение мощности заносят эффекты неэлектрической природы. Так, к примеру, в хим источнике мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе Воздействие внутреннего сопротивления на характеристики двухполюсника

Эффект внутреннего сопротивления является неотъемлемым свойством любого двухполюсника. Основной итог наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.

Если к источнику с [3] генератора напряжения E и активным внутренним сопротивлением r подключена нагрузка с сопротивлением R, то ток, напряжение и мощность в нагрузке выражаются следующим образом:

Нахождение внутреннего сопротивления

Расчёт

Понятие расчет применимо к схеме (но не к реальному устройству). Расчёт приведён для варианта чисто активного внутреннего сопротивления (отличия реактивного сопротивления подвергнутся рассмотрению дальше).

Примечание: Строго говоря, хоть какой реальный импеданс (в том числе и внутреннее сопротивление) обладает некоторой реактивной составляющей, так как хоть какой проводник имеет паразитную индуктивность и емкость. Когда мы говорим о чисто активном сопротивлении, то имеем в виду не реальную систему, а ее эквивалентвую схему, содержащую только резисторы: реактивность была отброшена как несущественная при переходе от реальной устройства к его эквивалентной схеме. Если же реактивность существенна при рассмотрении реального устройства, то эквивалентная схема составляется с учетом этой реактивности. Более тщательно смотри в статье « режиме холостого хода и ток в режиме недлинного замыкания двухполюсника. В данном случае система (1) записывается следующим образом:

где Uoc — выходное напряжение в режиме холостого хода (англ. open circuit ), другими словами при нулевом токе нагрузки; Isc — ток нагрузки в режиме недлинного замыкания (англ. short circuit ), другими словами при нагрузке с нулевым сопротивлением. Тут учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме недлинного замыкания равны нулю. Из последних уравнений сразу получаем:

Таким макаром, дабы расчитать внутреннее сопротивление и ЭДС эквивалентного генератора для двухполюсника, электрическая схема которого известна, нужно:

Расчитать выходное напряжение двухполюсника в режиме холостого хода
Расчитать выходной ток двухполюсника в режиме недлинного замыкания
На основании приобретенных значений отыскать r и U по формуле (2).

Измерение

Понятие измерение применимо к реальному устройству (но не к схеме). Конкретное измерение Реактивное внутреннее сопротивление

Если эквивалентная схема двухполюсника содержит реактивные элементы — способом всеохватывающих амплитуд .

Можно находить разные характеристики всеохватывающего значения: аргумент, только вещественную либо надуманную часть, также всеохватывающее число стопроцентно. Соответственно, методика измерений будет зависеть от того, что желаем получить.
Хоть какой из перечисленных характеристик находится в зависимости от частоты. На теоретическом уровне, дабы получить методом измерения полную информацию о реактивном внутреннем сопротивлении, нужно снять зависимость от частоты, другими словами провести измерения на всех частотах, которые может генерировать источник данного двухполюсника.

Использование

Почти всегда следует гласить не о применении внутреннего сопротивления, а об учете его негативного воздействия, так как внутреннее сопротивление является быстрее нехорошим эффектом. Все же, в некоторых системах наличие внутреннего сопротивления с номинальным значением является просто нужным.

Упрощение эквивалентных схем

Основная статья: Согласование источника и нагрузки

Согласование источника и нагрузки — это выбор соотношения сопротивления нагрузки и внутреннего сопротивления источника с целью заслуги данных параметров приобретенной системы (обычно, стараются достигнуть наибольшего значения какого-нибудь параметра для данного источника). Более нередко применяются следующие типы согласования:

Согласование по напряжению — получение в нагрузке наибольшего напряжения. Для этого сопротивление нагрузки должно быть как можно бо́льшим, по последней мере, много больше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме холостого хода. При всем этом очень достижимое в нагрузке напряжение равно ЭДС генератора напряжения U. Данный тип согласования применяется в электронных системах, когда носителем сигнала является напряжение, и его нужно передать от источника к нагрузке с наименьшими потерями.
Согласование по току — получение в нагрузке наибольшего тока. Для этого сопротивление нагрузки должно быть как можно наименьшим, по последней мере, много меньше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме недлинного замыкания. При всем этом очень достижимый в нагрузке ток равен Imax=U/r. Применяется в электронных системах, когда носителем сигнала является ток. К примеру, при съеме сигнала с быстродействующего фотодиода целенаправлено использовать преобразователь ток-напряжение с наименьшим входным сопротивлением. Маленькое входное сопротивление также решает делему заужения полосы из-за паразитного RC— коэффициента бегущей волны в полосы передачи (в СВЧ технике и теории длинноватых линий ). Практически то же самое, что и согласование по мощности, но применительно к Снижение больших напряжений

Время от времени к источнику искусственно добавляют огромное сопротивление (оно добавляется к внутреннему сопротивлению источника) для того, дабы существенно снизить получаемое от него напряжение. Но добавление конденсаторные блоки питания . Аналогично, с помощью емкостного отвода от высоковольтной Ограничения

Понятие внутреннего сопротивления вводится через эквивалентную схему, потому имеют силу Примеры

Значения внутреннего сопротивления относительны: то, что считается малым, к примеру, для гальванического элемента, является очень огромным для массивного аккума. Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r. Элементарные случаи двухполюсников без источников обсуждены особо.

Лабораторная работа № 4.21

Приборы и принадлежности: Блок генератора напряжений ГН1, блок амперметра-вольтметра АВ1, щит с объектами исследования С3-ЭМ01, соединительные провода.

Короткие теоретические сведения

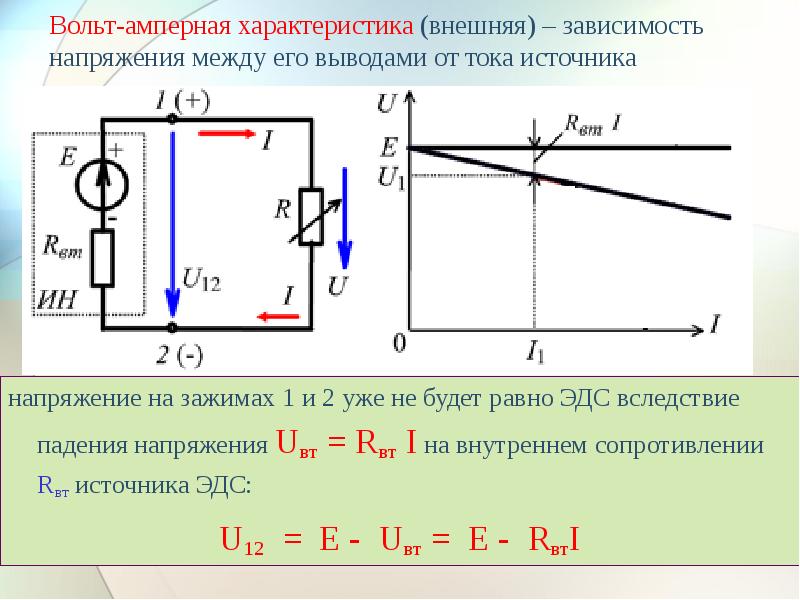
Принципная схема работы любого источника напряжения приведена на рис. 1, где   ЭДС источника, r  его внутреннее сопротивление, R  сопротивление наружной цепи (нагрузка). По закону Ома для замкнутой цепи сила тока

. (1)

Из закона Ома для однородного участка вытекает выражение для напряжения на нагрузке

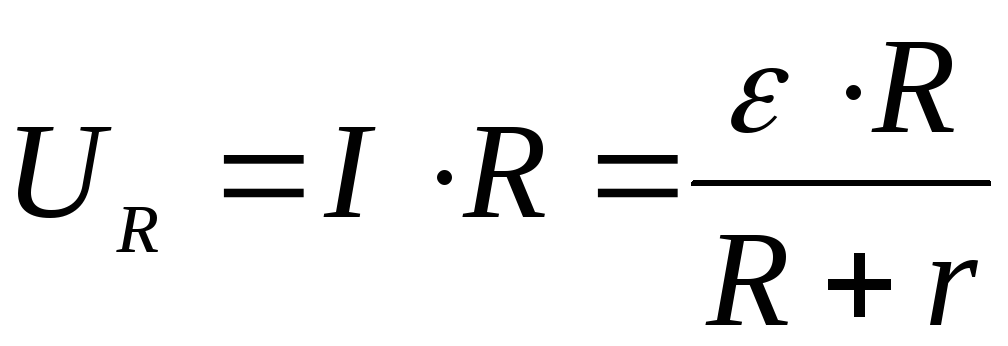
. (2)

Выражая из (1) сопротивление R и подставляя в (2) получим зависимость напряжения на нагрузке от силы тока в цепи

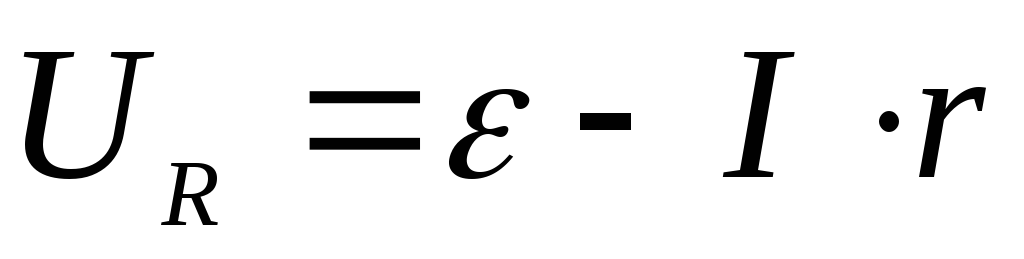
(3)

(физический смысл последней формулы очевиден  ЭДС, действующая в контуре, равна сумме падений напряжений во наружной части цепи и на внутреннем сопротивлении источника). Из последней формулы видно, что данная зависимость является линейной (ее график приведен на рис.2, нанесенные на рисунке кресты обозначают экспериментальные данные, которые в безупречном случае все должны лежать на прямой, но из-за погрешностей опыта такое случается изредка). Также видно, что при

где IКЗ =ε/r – ток недлинного замыкания.

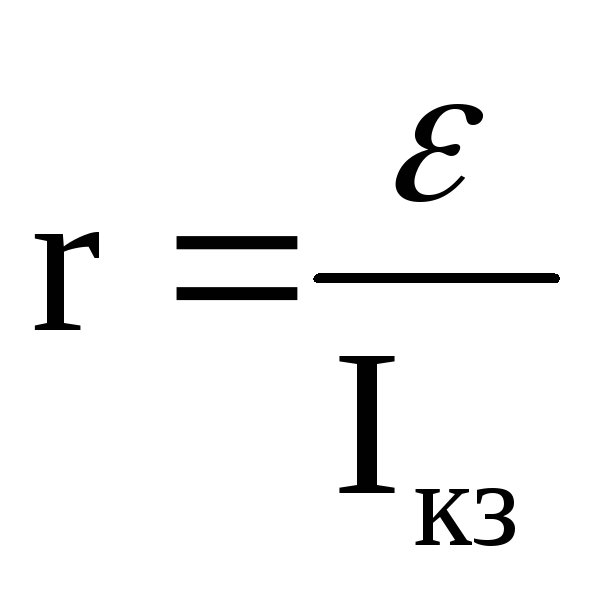
Данные характеристики зависимости (3) лежат в базе 1-го из способов экспериментального определения ЭДС источника и его внутреннего сопротивления. Для этого строится график зависимости напряжения на нагрузке от силы тока, который экстраполируется до скрещения с осями. Точка скрещения с осью напряжений дает значение ЭДС. Точка скрещения с осью тока дает ток недлинного замыкания IКЗ, который позволяет отыскать (при известной ЭДС) внутреннее сопротивление по формуле .

Нужная мощность, развиваемая источником, (мощность, выделяемая на нагрузке R)

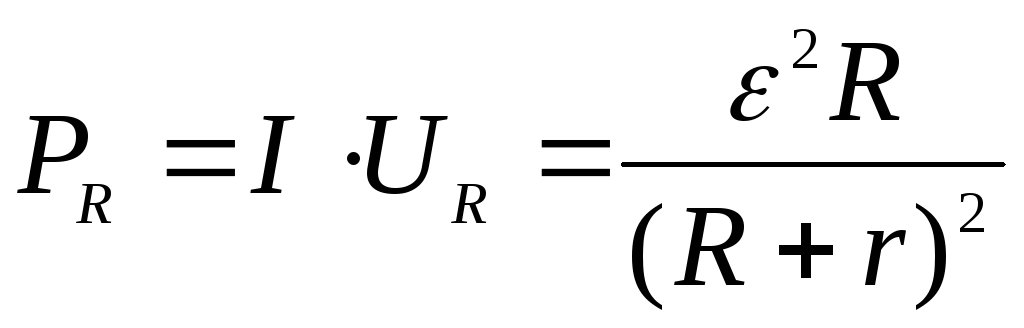
. (4)

График зависимости PR(R) приведен на рис. 3. Он представляет кривую, начинающуюся из нуля, вырастающую до предела, а потом снова спадающую до нуля при R = . Для определения сопротивления RMAX обеспечивающего наивысшую мощность нужно взять производную от (4) по R и приравнять ее к нулю. Наибольшая мощность во наружной цепи выделяется при наружном сопротивлении равном внутреннему сопротивлению источника

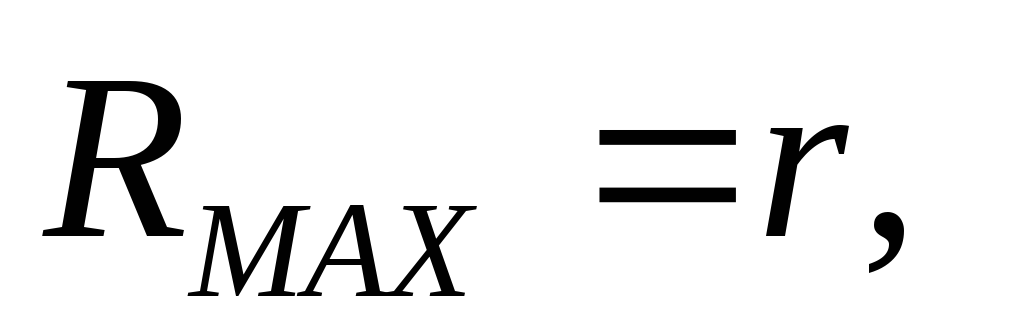
(5)

. (6)

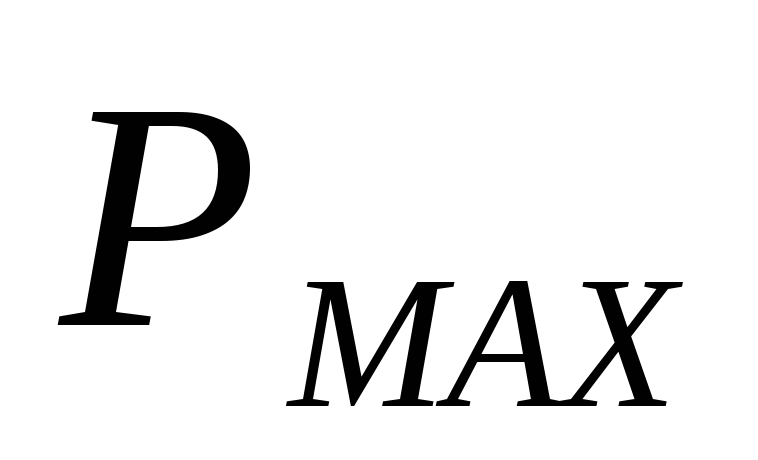
где -максимальная мощность в цепи

Зависимость (5) позволяет найти внутреннее сопротивление еще одним методом  построив зависимость мощности, выделяемой во наружной части цепи, от величины нагрузки и определив сопротивление, обеспечивающее максимум мощности.

Коэффициентом полезного деяния источника тока именуется отношение мощности выделяемой во наружной цепи PR =IUR к полной мощности развиваемой источником P = I

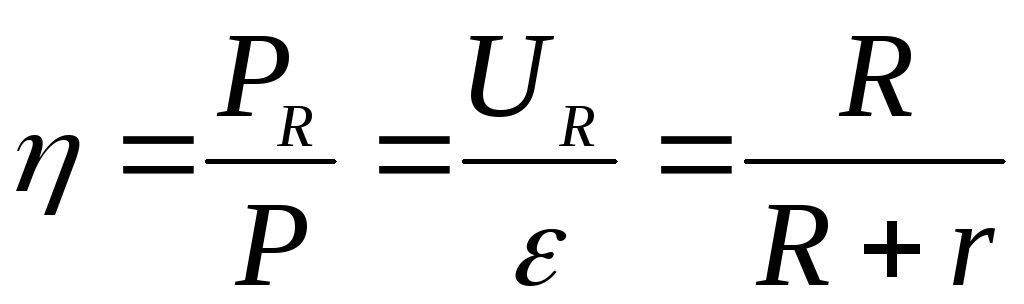
. (7)

Из последней формулы видно, что в случае выделения полезной наибольшей мощности КПД источника равен 0.5.

Порядок выполнения работы

Принципная электрическая схема, применяемая в лабораторной работе, приведена на рис.4. В качестве источника ЭДС применяется генератор регулируемого неизменного напряжения блока ГН1 с включенным внутренним сопротивлением (кнопка Rвн должна быть нажата). Переменное сопротивление находится на щите с объектами исследования С3-ЭМ01.

1. Соберите схему (рис. 4).

2. Меняя переменное сопротивление R (от 100 до 1500 Ом) вращая регулятор потенциометра на блоке сопротивлений, снимите зависимость напряжения UR и силы тока в цепи I от величины сопротивления R. Результаты внесите в таблицу 1.

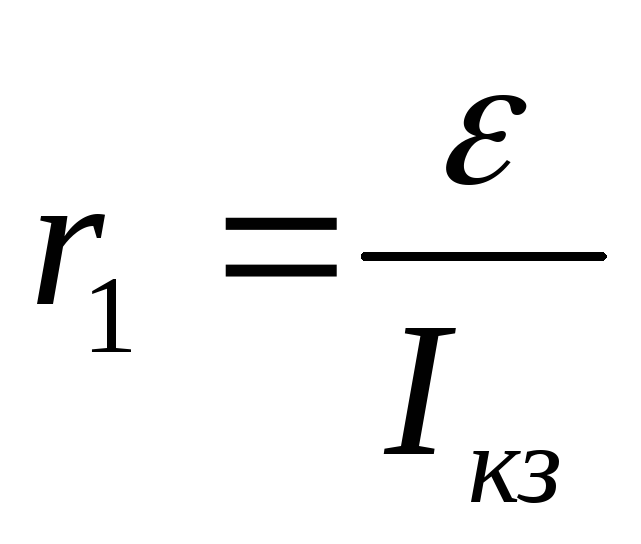
3. По данным таблицы постройте зависимость напряжения на нагрузке UR от силы тока в цепи согласно примеру изображенному на рис. 1. Экстраполируя график до скрещения с осями обусловьте ЭДС источника 1, ток недлинного замыкания IКЗ. По формуле обусловьте внутреннее сопротивление источника r1. Результаты внесите в таблицу 1.

4. По формуле (6), используя значения 1 и r1, обусловьте теоретическое значение наибольшей мощности во снаружи цепи PMAX1. Итог внесите в таблицу 1.

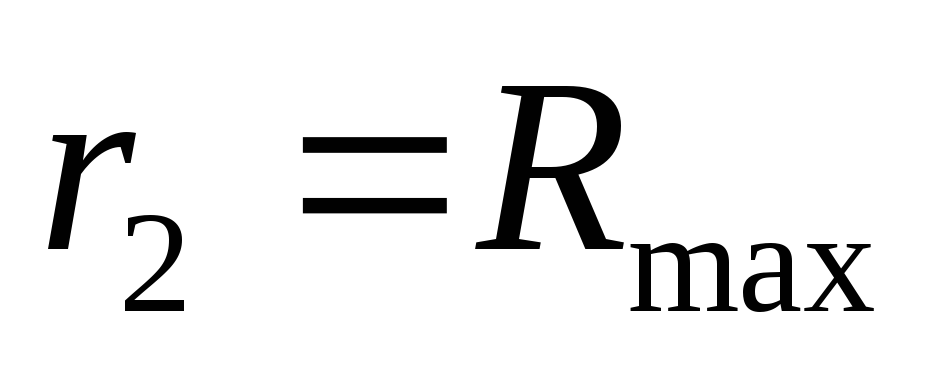
5. Используя данные таблицы 1, обусловьте мощность, выделяемую во наружной цепи по формуле: PR=IUR при каждом сопротивлении нагрузки R. Итог внесите в таблицу 1. По данным таблицы постройте график зависимости PR от R согласно рис. 3. По графику обусловьте максимум мощности и соответственное ему сопротивление Rmax, обусловьте внутреннее сопротивление источника r2 по формуле и наивысшую мощность во наружной цепи PMAX2 по графику. Результаты внесите в таблицу 1.

6. Отключив внутреннее сопротивление генератора при помощи кнопки «Rвн», обусловьте его ЭДС 2. Для этого подключите вольтметр к выходам ГН1. Запишите приобретенный итог в таблицу 1.

Сравните значения ЭДС , внутреннего сопротивления r и полезной наибольшей мощности PMAX приобретенные различными способами. Растолкуйте вероятное несовпадение результатов.

ИНФОФИЗ

Нередко сталкиваюсь с тем, что малыши не веруют в то, что могут обучаться и научиться, считают, что обучаться очень тяжело.

Урок 31. Лабораторная работа № 08. Измерение ЭДС и внутреннего сопротивления источника тока.

Лабораторная работа № 8

Тема: «Определение электродвижущей силы и внутреннего сопротивления источника тока».

Цель: научиться определять электродвижущую силу и внутреннее сопротивление источника электроэнергии.

Оборудование: 1. Амперметр лабораторный;

2. Источник электроэнергии;

3. Соединительные провода,

4. Набор сопротивлений 2 Ом и 4 Ом;

5. Переключатель однополюсный; ключ.

Появление разности потенциалов на полюсах любого источника является результатом разделения в нем положительных и отрицательных зарядов. Это разделение получается благодаря работе, совершаемой посторонними силами.

Силы неэлектрического происхождения, действующие на свободные носители заряда со стороны источников тока, именуются посторонними силами.

При перемещении электрических зарядов по цепи неизменного тока посторонние силы, действующие снутри источников тока, совершают работу.

Физическая величина, равная отношению работы Aст посторониих сил при перемещении заряда q снутри источника тока к величине этого заряда, именуется электродвижущей силой источника (ЭДС):

ЭДС определяется работой, совершаемой посторонними силами при перемещении единичного положительного заряда.

Электродвижущая сила, как и разность потенциалов, измеряется в вольтах [В].

Дабы измерить ЭДС источника, нужно присоединить к нему вольтметр при разомкнутой цепи .

Источник тока является проводником и всегда имеет некоторое сопротивление, потому ток выделяет в нем тепло. Это сопротивление именуют внутренним сопротивлением источника и обозначают r.

Если цепь разомкнута, то работа посторониих сил преобразуется в потенциальную энергию источника тока. При замкнутой цепи эта возможная энергия расходуется на работу по перемещению зарядов во наружной цепи с сопротивлением R и во внутренней части цепи с сопротивлением r , т.е. ε = IR + Ir .

Если цепь состоит из наружной части сопротивлением R и внутренней сопротивлением r, то, согласно закону сохранения энергии, ЭДС источника будет равна сумме напряжений на наружном и внутреннем участках цепи, т.к. при перемещении по замкнутой цепи заряд ворачивается в начальное положение , где IR – напряжение на наружном участке цепи, а Ir — напряжение на внутреннем участке цепи.

Таким макаром, для участка цепи, содержащего ЭДС:

Эта формула выражает закон Ома для полной цепи: сила тока в полной цепи прямо пропорциональна электродвижущей силе источника и назад пропорциональна сумме сопротивлений наружного и внутреннего участков цепи.

ε и r можно найти опытным методом.

Нередко источники электроэнергии соединяют между собой для питания цепи. Соединение источников в батарею может быть последовательным и параллельным.

При последовательном соединении два примыкающих источника соединяются разноименными полюсами.

Т.е., для последовательного соединения аккумов, к ″плюсу″ электрической схемы подключают положительную клемму первого аккума. К его отрицательной клемме подключают положительную клемму второго аккума и т.д. Отрицательную клемму последнего аккума подключают к ″минусу″ электрической схемы.

Получившаяся при последовательном соединении аккумуляторная батарея имеет ту же емкость, что и у одиночного аккума, а напряжение таковой аккумуляторной батареи равно сумме напряжений входящих в нее аккумов. Т.е. если батареи имеют однообразные напряжения, то напряжение батареи равно напряжению 1-го аккума, умноженному на количество аккумов в аккумуляторной батарее.

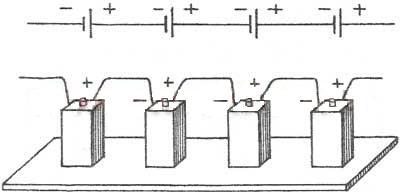
1. ЭДС батареи равна сумме ЭДС отдельных источников ε= ε1 + ε2 + ε3

2. Общее сопротивление батареи источников равно сумме внутренних сопротивлений отдельных источников rбатареи= r1 + r2 + r3

Если в батарею соединены n одинаковых источников, то ЭДС батареи ε= nε1, а сопротивление rбатареи= nr1

3. Сила тока в таковой цепи по закону Ома

При параллельном соединении соединяют между собой все положительные и все отрицательные полюсы 2-ух либо n источников.

Т.е., при параллельном соединении, батареи соединяют так, дабы положительные клеммы всех аккумов были подключены к одной точке электрической схемы (″плюсу″), а отрицательные клеммы всех аккумов были подключены к другой точке схемы (″минусу″).

Параллельно соединяют только источники с одинаковой ЭДС. Получившаяся при параллельном соединении аккумуляторная батарея имеет то же напряжение, что и у одиночного аккума, а емкость таковой аккумуляторной батареи равна сумме емкостей входящих в нее аккумов. Т.е. если батареи имеют однообразные емкости, то емкость аккумуляторной батареи равна емкости 1-го аккума, умноженной на количество аккумов в батарее.

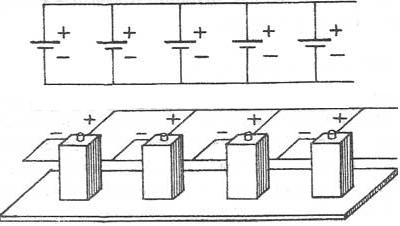
1. ЭДС батареи одинаковых источников равна ЭДС 1-го источника. ε= ε1= ε2 = ε3

2. Сопротивление батареи меньше, чем сопротивление 1-го источника rбатареи= r1/n
3. Сила тока в таковой цепи по закону Ома

Электрическая энергия, скопленная в аккумуляторной батарее равна сумме энергий отдельных аккумов (произведению энергий отдельных аккумов, если батареи однообразные), независимо от того, как соединены батареи — параллельно либо последовательно.

Внутреннее сопротивление аккумов, сделанных по одной технологии, приблизительно назад пропорционально емкости аккума. Потому т.к.при параллельном соединении емкость аккумуляторной батареи равна сумме емкостей входящих в нее аккумов, т.е возрастает, то внутреннее сопротивление миниатюризируется.

Видео: Внутреннее сопротивление

Читайте по теме: Кабель для розеток в квартире