На заряд, перемещающийся в магнитном поле, со стороны этого поля действует сила, именуемая силой Лоренца. При всем этом направление этой силы не совпадает с направлением магнитных линий поля. Побеседуем о методике определения этого направления.
Сила Лоренца
Длительное время магнетизм и электричество числились малосвязанными явлениями. Только к середине XIX в. опыты Х. Эрстеда и А. Ампера выявили такую связь. На базе исследовательских работ А. Ампера, Ж. Био, Ф. Савара, П. Лапласа были выведены законы, точно описывающие связь между электрическим током, возникающим магнитным полем и величину силы взаимодействия между ними.
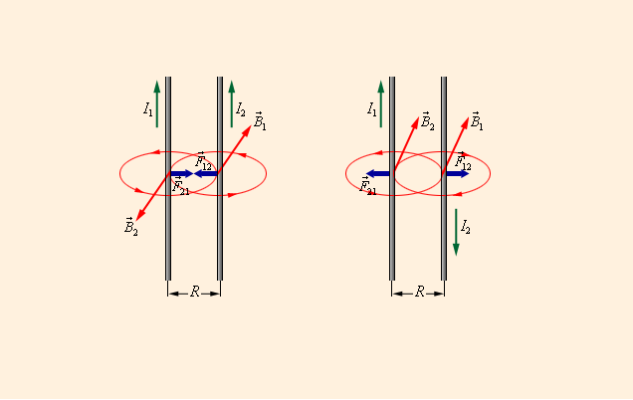
Рис. 1. Взаимодействие проводника с током тока и магнита.
Силу, с которой магнитное поле действует на проводник с током, окрестили силой Ампера. Но механизм ее появления был раскрыт только к концу XIX в. Х. Лоренцем. К этому времени уже установили, что электрический ток представляет собой упорядоченное движение заряженных частиц, и магнитное поле действует конкретно на заряженные частички. Силы, с которыми магнитное поле действует на любой из перемещающихся зарядов, соединяются в одну общую силу, которая и является силой Ампера.
Поэтому, сила Ампера — это проявление более общей силы, нареченной потом силой Лоренца. Формула силы Лоренца:
$$F_L = qvB sin \alpha$$
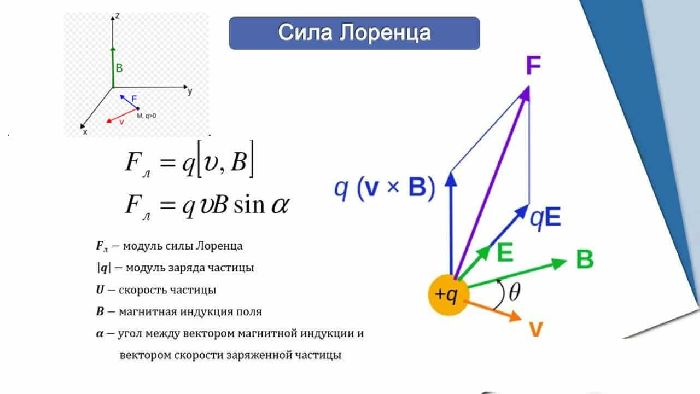
Рис. 2. Сила Лоренца.
Направление силы Лоренца
В формулу силы Лоренца заходит принципиальный параметр — угол $\alpha$. Это угол между векторами скорости движения заряда и магнитной индукцией. Присутствие этого элемента в формуле неслучайно. Дело в том, что направление деяния силы Лоренца не совпадает ни с вектором скорости движения заряда, ни с вектором магнитной индукции.
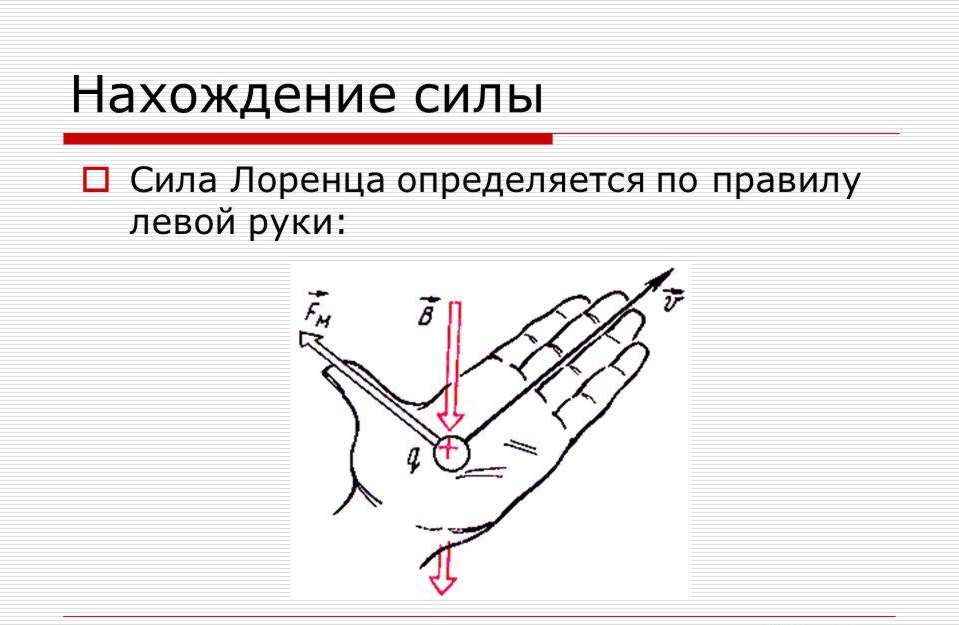
Сила Лоренца ориентирована перпендикулярно плоскости, образованной вектором скорости движения заряда и вектором магнитной индукции. Для определения этого направления принято мнемоническое правило левой руки: если четыре вытянутых пальца левой руки указывают направление движения положительного заряда, а полосы магнитного поля входят в ладонь, «прокалывая» ее, то отставленный большой палец покажет направление силы Лоренца.
Примеры применения правила левой руки
Разглядим определенные примеры, в каких сила Лоренца определяется по правилу левой руки.
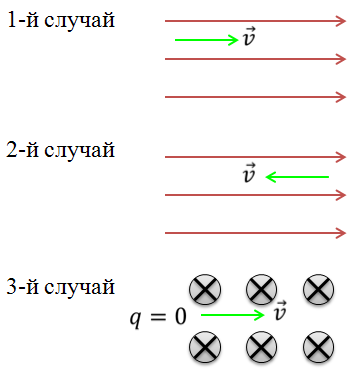
Допустим, протон движется вперед, северный магнитный полюс находится понизу, южный — вверху, куда будет ориентирована сила Лоренца?
Правило левой руки определено для положительно заряженной частички. Протон — положительно заряжен, поэтому четыре пальца нужно расположить по направлению его скорости — другими словами, вперед. Полосы магнитной индукции выходят из северного полюса и приходят к южному. Поэтому, в рассматриваемом случае они ориентированы снизу ввысь. Располагаем руку ладонью вниз, дабы магнитные полосы входили в ладонь (четыре пальца как и раньше ориентированы вперед).
Отставленный большой палец левой руки покажет вправо. Туда и будет ориентирована сила Лоренца при описываемых критериях.
Другой пример. Пусть электрон движется справа влево, северный полюс будет сверху. Куда ориентирована сила Лоренца?
Электрон заряжен негативно, для электрона четыре пальца должны быть ориентированы против его движения, другими словами, вправо. Ладонь при всем этом должна глядеть ввысь. Отставленный большой палец укажет направление вперед. Это и будет направление силы Лоренца в этом случае.
Сила Лоренца перпендикулярна плоскости, образованной векторами движения заряда и магнитной индукции. Если эти вектора лежат на одной прямой, то плоскости они не образуют — величина силы Лоренца равна нулю, и ее направление найти нереально.
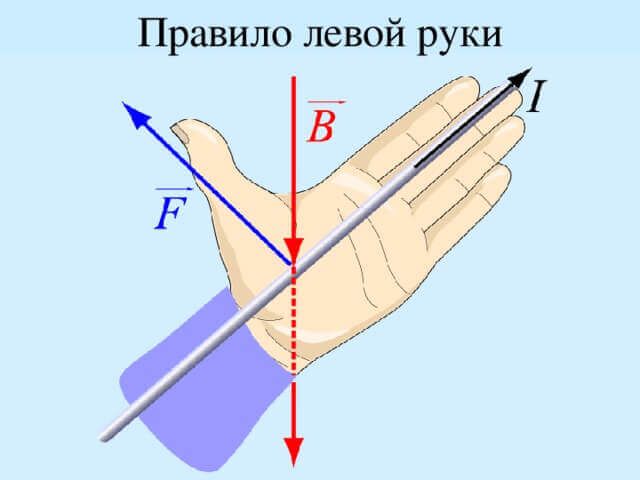
Рис. 3. Правило левой руки.
Что мы узнали?
Сила Лоренца действует на заряд, перемещающийся в магнитном поле. Эта сила ориентирована перпендикулярно плоскости, образованной векторами скорости и магнитной индукции. Для комфортного определения направления силы Лоренца применяется мнемоническое правило левой руки.
Сила Лоренца

Как понятно, на хоть какой перемещающийся в магнитном поле заряд действует сила Лоренца (если только он не двигается параллельно линиям магнитной индукции). На данном уроке мы разберём задачи на силу Лоренца.

На этот момент вы не сможете поглядеть либо пораздавать видеоурок ученикам
Дабы получить доступ к этому и другим видеоурокам комплекта, для вас необходимо добавить его в личный кабинет, приобретя в каталоге.
Получите неописуемые способности

1. Откройте доступ ко всем видеоурокам комплекта.

2. Раздавайте видеоуроки в личные кабинеты ученикам.

3. Смотрите статистику просмотра видеоуроков учениками.
Получить доступ
Конспект урока "Сила Лоренца"
«Великая книжка природы
написана языком математики».
Галилео Галилей
Эта тема посвящена решению задач на силу Лоренца.
Задачка 1. Протон влетает в однородное магнитное поле с исходной скоростью 20 Мм/с под углом 45º к направлению линий магнитной индукции. Найдите модуль вектора магнитной индукции этого поля, если на протон действует сила 4×10 –13 Н.
Сила Лоренца определяется по формуле
Тогда модуль вектора магнитной индукции равен
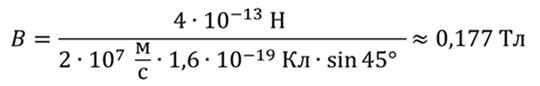
Ответ: 177 мТл.
Задачка 2. Электрон влетает в магнитное поле с индукцией 25 мкТл. Обусловьте радиус кривизны линии движения, по которой электрон будет двигаться, если направление его исходной скорости перпендикулярно направлению линий магнитной индукции. Исходная скорость электрона равна 630 км/с.
Применим правило левой руки: если расположить левую руку так, что полосы магнитной индукции входят в ладонь, а четыре пальца указывают направление скорости, то отогнутый большой палец укажет направление силы Лоренца, которая будет действовать на положительный заряд. Электрон имеет отрицательный заряд, потому сила Лоренца ориентирована в обратную сторону.
Сила Лоренца определяется по формуле
Согласно второму закону Ньютона
Центростремительное ускорение равно отношению квадрата скорости к радиусу кривизны линии движения, а синус девяноста градусов равен единице, тогда получаем, что
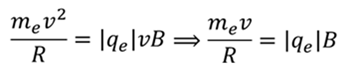
Тогда радиус кривизны линии движения равен
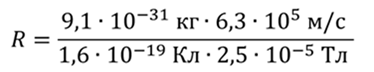
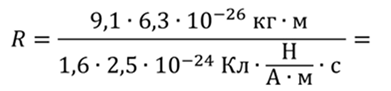
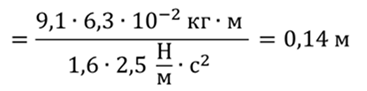
Ответ: 14 см.
Задачка 3. Частичка влетает в однородное магнитное поле и пролетает через него без конфигурации линии движения. В каких случаях это может быть?
Траектория перемещения частички не будет изменяться если сила Лоренца будет равна нулю.
Запишем формулу для определения силы Лоренца
Данное произведение будет равно нулю в этом случае, если один из множителей равен нулю. По условию задачи скорость и индукция поля не равны нулю. Поэтому,
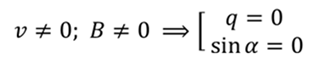
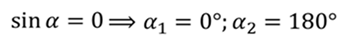
Ответ: или частичка двигается параллельно линиям магнитной индукции, или она не имеет заряда.
Задачка 4. В однородном магнитном поле с индукцией 0,2 мТл по окружности движется частичка. Найдите время, за которое направление скорости частички поменяется на обратное, если заряд частички равен 60 нКл, а масса – 2×10 –13 кг.
Запишем формулу, по которой рассчитывается сила Лоренца
При любом криволинейном движении тело движется с центростремительным ускорением.
Запишем 2-ой закон Ньютона
С учётом того, что центростремительное ускорение равно отношению квадрата скорости к радиусу кривизны линии движения, получим
Приравняем выражения для определения радиуса кривизны
Т.к время есть отношение пройденного пути к скорости, то
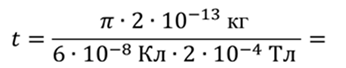
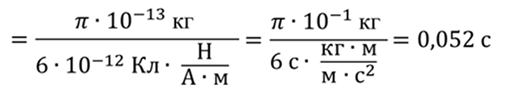
Ответ: 52 мс.
Задачка 5. Протон, пройдя ускоряющую разность потенциалов 60 В, влетел в однородное магнитное поле с индукцией 5×10 –2 Тл. Считая, что протон крутится в плоскости, перпендикулярной линиям магнитной индукции, найдите радиус кривизны линии движения и частоту вращения.
Запишем формулу для определения силы Лоренца
При любом криволинейном движении тело двигается с центростремительным ускорением. Исходя из этого, запишем 2-ой закон Ньютона
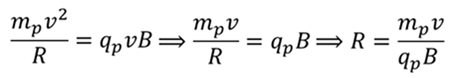
Хоть какое движущееся тело обладает кинетической энергией
Работа электрического поля по переносу заряда определяется как
Конкретно работа электрического поля, в этом случае, перебегает в кинетическую энергию протона. Потому получаем
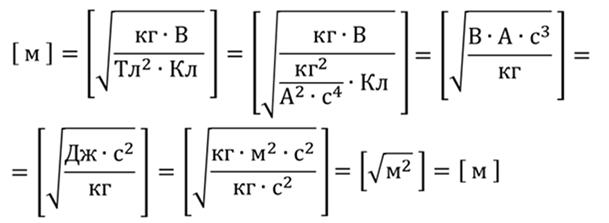
Выразим скорость и подставим её в формулул для определения радиуса кривизны линии движения
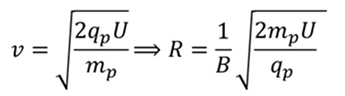
Частота вращения определяется по формуле
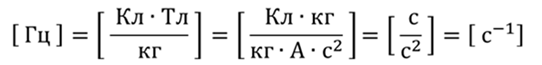
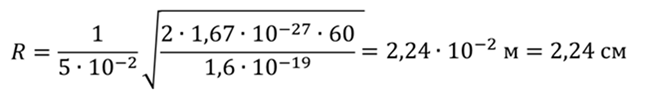
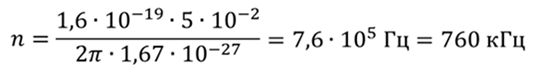
Ответ: радиус кривизны линии движения – 2,24 см; частота вращения – 760 кГц.