Для хоть какой, сколь угодно сложной цепи неизменного тока, можно составить энергетический баланс, вытекающий конкретно из закона сохранения энергии: алгебраическая сумма всех мощностей источников энергии равна сумме всех мощностей приемников энергии:
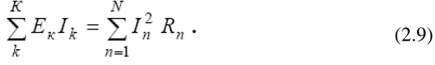
В этой формуле К — число источников энергии цепи; N — число приемников энергии цепи. Во всех приемниках энергии токи и напряжения имеют одно и то же направление. Потому правая часть уравнения (2.9) является арифметической суммой мощностей всех приемников цепи. Что касается левой части этого уравнения, то в некоторых ветвях сложной цепи ток ветки возможно окажется направленным обратно действию ЭДС источника энергии. Тогда произведение EI выходит отрицательным. На физическом уровне это значит, что при таком режиме работы рассматриваемый источник не генерирует энергию, а потребляет ее (к примеру, аккумулятор при его зарядке).
Переходные процессы
Переходные процессы в электрической цепи — это электромагнитные процессы, происходящие при изменении ее состояния в течение недлинного промежутка времени. Конденсаторы в цепи могут владеть энергией электрического поля, а катушки индуктивности — энергией магнитного поля. В переходном процессе эта энергия должна перераспределиться между этими полями либо выделиться в виде тепла. Этот процесс занимает какое-то время, называемое временем переходного процесса.
Секундное изменение схемы соединения либо характеристик частей электрической цепи именуется коммутацией. На схеме обычно коммутация указывается в виде рубильника со стрелкой (рис. 2.4).
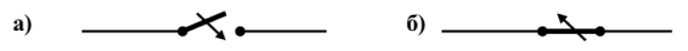
Рис. 2.4. Ключ коммутации: а) стрелка значит включение рубильника; б) стрелка значит отключение рубильника
При анализе переходных процессов отсчёт времени создают от момента коммутации t = 0 и вводят понятия момента времени, конкретно предыдущего коммутации t = 0 , и момента времени, конкретно следующего за коммутацией, t = 0+ .

Ток в ветки с индуктивным элементом не может поменяться скачкообразно и после коммутации сохраняет значение, которое было до коммутации. Этот вывод именуется первым законом коммутации и записывается в виде:
Напряжение на емкостном элементе не может поменяться скачкообразно. Этот вывод именуется вторым законом коммутации и записывается так:

Разглядим случаи, когда коммутации происходят в цепи с последовательно включенными источником, резистором и конденсатором. Подробные выводы аналитических выражений опустим, их можно поглядеть в учебниках по электротехнике, тут же приведем только графики зависимостей.
При разрядке конденсатора через резистор (рис. 2.5) напряжение на конденсаторе Uc плавненько миниатюризируется от ЭДС источника до нуля. Ток при коммутации / увеличивается скачком, потом плавненько миниатюризируется.
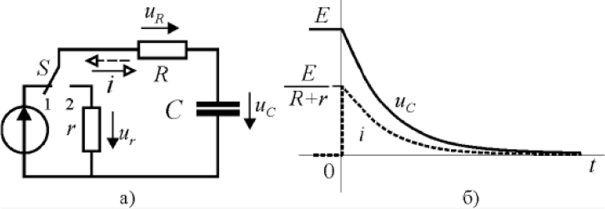
Рис. 2.5. Разряд конденсатора
При подключении конденсатора к источнику неизменного напряжения через резистор (рис. 2.6) напряжение плавненько возрастает до напряжения источника, а ток изменяется скачком, от нуля до Imax = E/R , потом плавненько миниатюризируется до нуля.
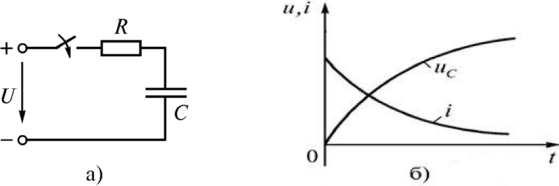
Рис. 2.6. Заряд конденсатора
Если сопротивление резистора либо цепи, через которую осуществляется зарядка — разрядка конденсатора, будет малым, то в цепи будет большой скачок тока. Это может быть вредным как для самой цепи, так и будет создавать помехи другим приемникам энергии.
Сейчас разглядим случаи, когда коммутации происходят в цепи с последовательно включенными источником, резистором и катушкой индуктивности. При замыкании ключа на источник (положение 1) катушка подключается к источнику ЭДС через резистор (рис. 2.7а). В катушке возникает ток. По закону самоиндукции при изменении тока в катушке появляется ЭДС самоиндукции. Эта ЭДС по правилу Ленца имеет таковой символ, дабы препятствовать повышению тока. Потому происходит плавное нарастание тока от нуля до значения i = E/R (рис. 2.76). Напряжение на катушке Ul плавненько миниатюризируется от Е до нуля.
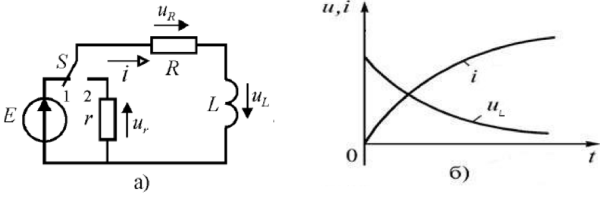
Рис. 2.7. Подключение индуктивности к источнику
Разглядим сейчас процессы, происходящие в цепи с катушкой индуктивности при размыкании цепи. Пусть безупречный ключ S долгое время находился в состоянии 1 так, что переходный процесс, связанный с скоплением энергии индуктивным элементом L закончился, а потом переключился в положение 2 (рис. 2.8а)
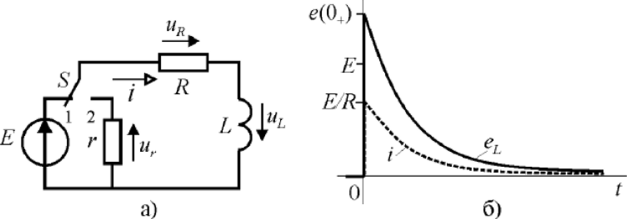
Рис.2.8. Отключение индуктивности от источника

После размыкания ключа S в цепи начинается переходный процесс, связанный с преобразованием энергии, скопленной в магнитном поле катушки, в тепло, рассеиваемое резистивными элементами R и г. Процесс преобразования завершается при понижении тока до нуля, т.е. при полном рассеянии скопленной энергии (рис 2.86). В момент коммутации на индуктивном элементе появляется ЭДС самоиндукции е(0+), превосходящая ЭДС источника в (1 + г / R ) раз.
Отключение цепи с индуктивным элементом без замыкания на сопротивление эквивалентно условию: г = оо , где г — сопротивление разомкнутых контактов ключа. В итоге на катушке и на ключе должно появляться нескончаемо огромное напряжение. По сути этого не происходит, т.к. уже при напряжении в несколько киловольт в зазоре контактов выключателя появляется электрическая дуга, которая имеет конечное электрическое сопротивление, снижающее перенапряжения. Все же, это явление представляет огромную опасность для оборудования и просит учета и принятия мер для уменьшения вредных последствий.
Самыми распространенными методами понижения перенапряжений в цепях неизменного тока являются включение конденсатора и резистора параллельно контактам ключа либо диодика и резистора параллельно катушке индуктивности (рис. 2.9).
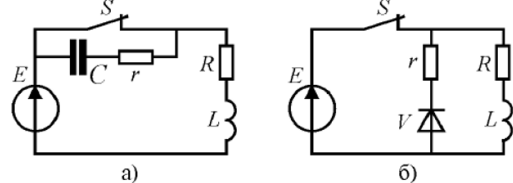
Рис. 2.9. Защита от перенапряжения при выключении индуктивности
При размыкании ключа S конденсатор начинает заряжаться (рис. 2.9а), создавая контур для протекания тока параллельно контактам ключа. Эту же функцию делает диодик на рис. 2.9 б. При замкнутом ключе S ЭДС источника сдвигает диодик в отрицательном направлении, в каком он обладает высочайшим сопротивлением. При размыкании ключа диодик сдвигается в положительном направлении за счет ЭДС самоиндукции и открывает путь для протекания тока, минуя ключ.
Мы разглядели случаи коммутации в цепи неизменного тока, но изготовленные выводы будут справедливыми и для промышленного переменного тока. Это разъясняется тем, что время переходных процессов нередко оказывается меньше периода переменного тока.
Вопросы для самопроверки
- 1. Что такое неизменный электрический ток?
- 2. Что такое электродвижущая сила (ЭДС)?
- 3. Какое направление принято считать положительным для электрического тока (напряжения)?
- 4. Сформулируйте закон Ома.
- 5. Как изменяется общее сопротивление последовательно соединенных резисторов при подключении нового элемента?
- 6. Как изменяется общая проводимость параллельно соединенных резисторов при подключении нового элемента?
- 7. Сформулируйте 1-ый (2-ой) закон Кирхгофа.
- 8. Почему алгебраическая сумма электрических токов в узлах цепи равна нулю?
- 9. Сформулируйте правило выбора символов в уравнениях, составляемых для узлов электрической цепи.
Ю.Сформулируйте правило выбора символов в уравнениях, составляемых для контуров электрической цепи.
Уравнение баланса мощностей для цепей неизменного тока
При решений электротехнических задач, нередко необходимо проверить корректность отысканных значений. Для этого в науке ТОЭ, существует так именуемый баланс мощностей.
Баланс мощностей – это выражение закона сохранения энергии, в электрической цепи. Определение баланса мощностей звучит так: сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками. Другими словами если источник ЭДС в цепи дает 100 Вт, то приемники в этой цепи потребляют ровно такую же мощность.
Проверим это соотношение на ординарном примере.
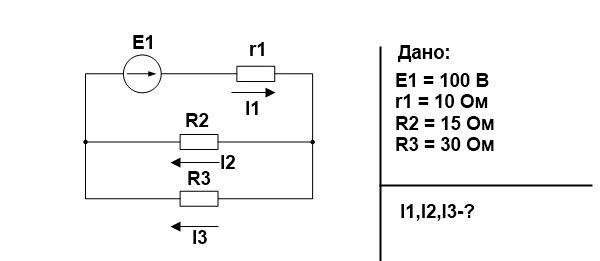
Для начала свернем схему и найдем эквивалентное сопротивление. R2 и R3 соединены параллельно.
Читайте также: Измеряя характеристики вращения: энкодеры bourns
Найдем по закону Ома ток источника и напряжение на R23, беря во внимание, что r1 и R23 соединены последовательно, поэтому, сила тока однообразная.
Сейчас проверим корректность при помощи баланса мощностей.
Маленькое различие в значениях связано с округлениями в процессе расчета.
При помощи баланса мощностей, можно проверить не только лишь ординарную цепь, но и сложную. Давайте проверим сложную цепь из статьи способ контурных токов.

Видите ли независимо от трудности цепи, баланс сошелся, и должен сойтись в хоть какой цепи!
Баланс мощностей для цепей неизменного тока — понятное разъяснение
Баланс мощностей: сумма мощностей, выделяемых источниками, равна сумме мощностей, потребляемых приемниками.
А сейчас давайте разглядим по порядку и на определенных примерах
, что такое баланс мощностей и как он составляется для разных
цепей неизменного тока
(о балансе мощностей цепи переменного тока, мы побеседуем позднее).
Дабы было более понятно, сходу разглядим пример.
Имеется схема цепи, изображенная на рисунке 1. Входные данные значение ЭДС E и сопротивление резистора R. Нужна составить баланс мощностей
для данной цепи.
Для начала необходимо найти ток:
Читайте также: Стойки для световых устройств своими руками
Следующим шагом определим мощности источника и приемника
. Так как это
цепь неизменного тока
(в цепи действует неизменный источник напряжения), то мощность, отдаваемая источником и мощность, потребляемая приемником, (в данной схеме цепи, приемник только один – это резистор R ) будет
активной
.
Определим активную мощность, отдаваемую источником напряжения E:
Pист=I·E=1·10=10 (Вт)
(Единица измерения активной мощности «Ватт»)
Активная мощность
обозначается буковкой P. Индекс “ист” сокращенно от “источников”.
Определяем активную мощность приемника:
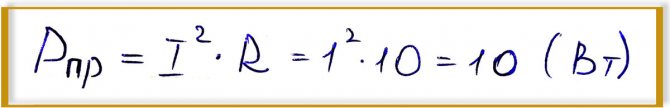
Для определения активной мощности источника, применяется формула произведения тока I через источник на величину E источника. Для определения активной мощности приемника, применяется формула произведения квадрата тока через приемник (в этом случае приемником является резистор R) на сопротивление этого резистора. Если ранее было понятно напряжение резистора, то можно применить формулу для нахождения активной мощности приемника:
(Индекс “пр” сокращенно от “приемников”).
Таким макаром, в источниках напряжения (ЭДС) происходит генерация электроэнергии
, а в элементе R происходит
потребление энергии
. Электрическая энергия преобразуется в термическую, т. е. резистор R потребляет электрическую энергию, отдаваемую источником E.
Отсюда следует правило баланса мощностей:
Читайте также: Ремонт вентиляторов своими руками: устройство и наладка
Для нашей задачи, схема цепи которой изображена на рисунке 1, запишем баланс активных мощностей
.
Баланс осуществляется
.
Для расчета электрических цепей и проверки корректности отысканных токов, делаем проверку баланса мощностей. Если приобретенная мощность приемников отличается от приобретенной мощности источников, то баланс мощностей нарушается
. Это гласит о том, что токи в цепи найдены ошибочно.
Погрешность баланса мощностей
может составлять до 3%.
Т. е отличие между Pист и Pпр не должно превосходить 3%. Для определения погрешности, пользуются следующей формулой:
В этом случае, погрешность равна нулю и баланс осуществляется
Разглядим следующий пример.
Нужна составить баланс мощностей для цепи, изображенной на рисунке 4.
Для начала определим ток в цепи. Резисторы R1 и R2 включены последовательно. Поэтому, общее сопротивление цепи, запишется как:
Тогда ток по закону Ома:
Так как все ЭДС и сопротивления известны, а ток в цепи мы отыскали, определим активную мощность источников и приемников.
Активная мощность, потребляемая резисторами, составляет 20 (Вт) Определим активную мощность источников.
Pист=I·E1+I·E3-I·E2=1·10+1·30-1·20=20 (Вт)
Активная мощность, отдаваемая всеми источниками ЭДС, составляет 20 (Вт)
Запишем баланс мощностей для данной цепи:
Баланс мощностей осуществляется, погрешность равна нулю.
В левой части равенства получили сумму мощностей, потребляемых приемниками, а в правой части равенства получили сумму мощностей, генерируемых источниками. В этом случае ЭДС E2 работает как приемник, к примеру, аккумулятор в режиме зарядки
Если действие ЭДС E и тока через Eсовпадают по направлению, то произведение E·I
берется со знаком “+”, если не совпадает, то “-“. В нашей цепи I и E2 ориентированы навстречу друг дружке, потому произведение
I·E2
взяли с минусом.
Мощность в цепи неизменного тока
Здрасти! Эту статью можно считать началом знакомства с электричеством. Напряжение, ток, сопротивление – это три главные величины, на которых построены главные законы электротехники и эти величины связаны между собой очередной – мощностью. А дабы было проще знакомиться с электротехникой, мы будем рассматривать мощность в цепи неизменного тока. Дело в том, что при расчетах в цепях переменного тока возникает достаточно много критерий. Вобщем, обо всём по порядку и вы на данный момент сами с этим разберётесь.
Для удобства я сходу напишу международные обозначения этих четырёх величин:
Читайте также: Как отыскать силу тока протекающего через катушку
U – напряжение (В, вольт)
R – сопротивление (Ом, ом)
P – мощность (Вт, ватт – не нужно путать с вольтом, который обозначается только одной буковкой В)

Для начала абстрактный пример, дабы проще было осознавать определения, которые я на данный момент буду применять. Допустим, есть магазин продуктов (условно это можно представить, как напряжение), есть средства (условно это будет ток), есть совесть, которая не позволяет для вас растрачивать много либо напротив, шепчет, дабы вы крупно потратились (это можно считать сопротивлением) и есть приобретенные продукты либо продукты, которые вы несёте домой (это мощность). Фактически, на этом примере можно разъяснить многие законы, связанные с электрическим током. Все обозначенные величины связаны между собой законом Ома, который говорит, что сила тока в цепи прямо пропорциональна напряжению и назад пропорциональна сопротивлению цепи, а конкретно:
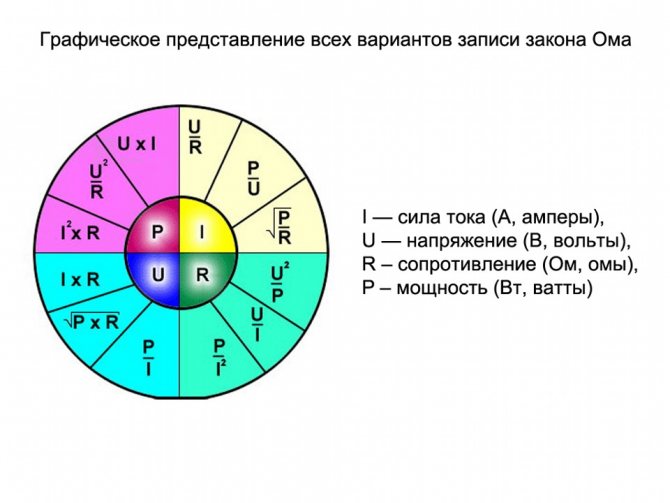
В абстрактном примере – чем больше магазин (напряжение) и чем меньше для вас шепчет совесть (сопротивление), тем больше вы тратите средств (сила тока), а когда вы несёте приобретенный продукт домой, вы совершаете работу (мощность). Мощность в цепи неизменного тока это и есть работа, совершаемая электричеством. Мощность это произведение тока на напряжение, а если заместо тока либо напряжения подставить надлежащие значения, то можно получить мнемоническую табличку:
Видите ли, мощность в цепи неизменного тока это достаточно обычное понятие, если малость вникнуть в материал. На самом деле, это всего две формулы с подменой значений. Как это смотрится:
Если сейчас в формуле мощности подставить место значения тока формулу тока, то получим следующее:
Конкретно таким макаром и вышло 12 формул на базе закона Ома, которые вы видите в мнемонической табличке. Что такое мощность в цепях неизменного тока мы более либо наименее разобрались, но есть ещё один момент.
Баланс мощностей в цепи неизменного тока.
Фактически, это просто проверка корректности расчетов электрической цепи. Ворачиваясь к нашему абстрактному примеру это смотрится так: вы приобрели продукты, забрали их на кассе, отошли от кассы и для вас показалось, что ваши пакеты должны быть больше либо меньше, чем вышли. Тогда вы берёте чек и начинаете ассоциировать продукт в чеке и продукт в наличии. Если продукты в чеке и продукты в руках совпали, означает всё в порядке. Если мы обратимся к определению, то баланс мощностей – сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками.
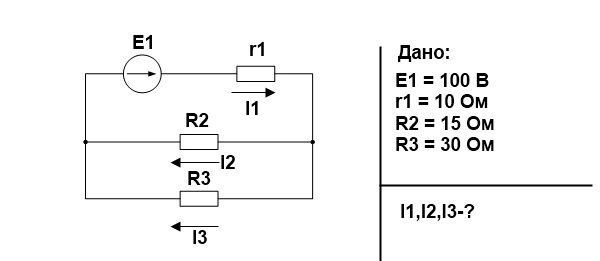
Как это применять на практике? Допустим, у нас есть задачка, которую необходимо решить:
Так как решение задачи не является целью этой статьи, я дам уже готовые ответы.
Сейчас нужно проверить верно ли были посчитаны токи в задачке. Ток в цепи равен току , поэтому, мощность источника питания (Е1хI1) должна быть равна сумме мощностей сопротивлений
Что мы и получаем с учетом утрат при округлениях.
Таким макаром, баланс мощностей в электрической цепи неизменного тока — это ничто другое, как проверка себя самого, собственных расчётов.
Видите ли, мощность в цепи неизменного тока посчитать достаточно просто. Еще больше сложностей возникнет, если ток будет переменный. Другими словами, на примере магазина это смотрится так:
Неизменный ток – от входа до выхода ровная линия и вы расслабленно идете от начала и до конца без каких-то приключений.
Переменный ток – магазин представляет из себя зигзаг и для вас приходится делать излишние движения.
МОЩНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА. БАЛАНС МОЩНОСТИ
КОНДЕНСАТОР В ЦЕПИ ПЕРЕМЕННОГО ТОКА
В цепи переменного тока происходит повторяющаяся зарядка и разрядка пластинок конденсатора (рис.4).
Заряд на пластинках конденсатора — q
Если переменное напряжение, подаваемое на пластинки конденсатора меняется по закону u = Umsin t , то
т.е. напряжение отстает от тока по фазе на π /2. Разделив правую и левую части выражения (5) на , получим закон Ома для действующих значений напряжения и тока емкостного элемента:
. Величина именуется емкостным сопротивлением.
В цепи переменного тока различают активную, реактивную и полную мощность.
Активная мощность – это средняя мощность необратимых преобразований электроэнергии за период – Р. Активную мощность определяют в ваттах (Вт):
, где — моментальная мощность.
Если напряжение и ток меняются по законам:
Беря во внимание, что , получим
— коэффициент мощности. Он указывает, какая часть электроэнергии перебегает в другие виды энергии и, а именно, применяется на выполнение полезной работы.
Реактивная мощность — . Это мощность колеблющейся энергии на реактивных элементах – катушке и конденсаторе. Она указывает, какая часть электроэнергии перебегает в энергию магнитного поля на катушке — и назад в электрическую. И какая часть электроэнергии перебегает в энергию электрического поля на конденсаторе — и назад в электрическую:
Реактивная мощность измеряется в вольт-амперах реактивных (вар). При > 0 (индуктивная нагрузка) > 0, а при
Полная мощность измеряется в вольт-амперах (ВА).
Если в треугольнике напряжений помножить все стороны на силу тока, то получим треугольник мощностей:
Для роста можно включить параллельно приемнику батарею конденсаторов, которая компенсирует реактивную мощность мощностью либо применять такие движки, у каких реактивный ток очень мал.
Из закона сохранения энергии следует, что:
1. Активная мощность источников в электрической цепи равна активной мощности потребителей:
Читайте также: Как верно заряжать (пополнять энергию) гелевый аккумулятор — полезные советы
2. Реактивная мощность источников в электрической цепи равна реактивной мощности потребителей:
3. Полная мощность источников в электрической цепи равна полной мощности потребителей:
Уравнения (1), (2), (3) именуют уравнениями баланса мощностей в цепи переменного тока.






