Поначалу прочтите статью " Лаконичный обзор темы: переменный электрический ток".
Мощность цепи переменного тока либо энергия, поступающая в цепь от источника (генератора, трансформатора) за единицу времени, находится по формуле:
где I и U — действующие значения тока и напряжения (определяются по свидетельствам амперметра и вольтметра);
угол "фи" — есть сдвиг фаз колебаний тока и напряжения.
Мощность цепи переменного тока очень сильно находится в зависимости от
именуемого коэффициентом мощности .
А конкретно, мощность воспринимает наибольшее значение, равное произведению силы тока на напряжение, когда колебания тока и напряжения происходят в одинаковой фазе (угол "фи" равен нулю).
Это имеет место, когда цепь переменного тока содержит только активную нагрузку (к примеру, содержит только лампы накаливания), когда в цепи нет конденсаторов и катушек индуктивности.
С уменьшением коэффициента мощности (из — за присутствия в цепи конденсатора и (либо) катушки индуктивности), нужная мощность цепи переменного тока миниатюризируется.
Дело в том, что конденсатор и катушка индуктивности (возникающие в них электрическое и магнитное поля) временами берут энергию от источника, а потом возвращают её источнику, другими словами энергия гуляет по проводам от источника к потребителю и назад — от потребителя к источнику (см. статьи " Конденсатор в цепи переменного тока" и " Катушка индуктивности в цепи переменного тока").
Если коэффициент мощности меньше единицы, то это означает, что не вся мощность источника (генератора, трансформатора) расходуется цепью. Для наглядности приведём результаты расчёта.
К примеру, мощность источника составляет 100 000 кВт, а коэффициент мощности цепи равен 0,8. Это означает, что источник может дать потребителю только 80 000 кВт, другими словами при коэффициенте мощности цепи, наименьшем единице, генератор и трансформатор не могут дать в сеть свою полную мощность.
Таким макаром, если коэффициент мощности потребителя энергии меньше единицы, то генераторы и трансформаторы отдают потребителю только часть мощности:
другими словами отдают наименьшую мощность, чем могли бы дать.
Чем ниже коэффициент мощности потребителя энергии, тем наименее прибыльно внедрение генераторов и трансформаторов, имеющих мощность, на которую они рассчитаны, другими словами равную произведению тока на напряжение.
(Генераторы и трансформаторы рассчитываются на некоторый наибольший ток. при котором их обмотки не перенагреваются, и на определённое напряжение).
Допустим, по проводам, идущим к потребителю, при коэффициенте мощности, наименьшем единицы, нужно передать полезную мощность Р.
Тогда ток в проводах должен быть равен отношению этой мощности к произведению напряжения на косинус фи (см. формулу для мощности). Отсюда следует, чем меньше косинус фи, тем больше должна быть сила тока в проводах, дабы передать ту же полезную мощность. Тогда провода обязаны иметь большее сечение, будет огромным расход цветных металлов на их изготовка. При всем этом будет теряться энергия в проводах.
Произнесенное выше гласит о значимости увеличения коэффициента мощности на промышленных предприятиях. Что для этого делается?
Если применяемые движки работают не на полную мощность, их подменяют на наименее массивные. Предпринимаются и другие меры.
Мы разглядим одну из них — это подсоединение параллельно катушке индуктивности конденсатора (либо батареи конденсаторов).
Дело в том, что в главном нагрузка на промышленных предприятиях имеет активно-индуктивный нрав, другими словами содержит активное и индуктивное сопротивления. К ним относятся такие потребители, как движки, индукционные печи, сварочные агрегаты и др., так как они содержат катушки индуктивности, владеющие активным и индуктивным сопротивлениями. О таких нагрузках говорилось ранее в статье " Катушка в цепи переменного тока"
Вспомним некоторые моменты из этой статьи.
Катушку в цепи переменного тока можно представить в виде последовательно соединённых активного сопротивления провода катушки и её индуктивного с опротивления .
Мощность в цепи переменного тока и коэффициент мощности (косинус φ)
В проф лексиконе электрика более популярны слова: фаза, ток, напряжение и словосочетание «косинус-фи». Этот «косинус-фи» всегда боль в голове промышленного энергетика. Попробуем популярно разъяснить причину такового почтения электриков к тригонометрической функции cos φ. «Косинус-фи» в электроэнергетике еще именуют коэффициентом мощности.
Коэффициент мощности охарактеризовывает потребителя электроэнергии исходя из убеждений наличия в нагрузке реактивной составляющей, при которой переменный ток и напряжение не совпадают по фазе. Коэффициент мощности указывает, как переменный ток в нагрузке двигается по фазе относительно напряжения на ней (отстает либо опережает). Численно коэффициент мощности равен косинусу этого фазового сдвига. В электроэнергетике для коэффициента мощности принято обозначение cos φ (где φ — угол сдвига по фазе между током и напряжением). При наличии в нагрузке реактивной составляющей наряду со значением коэффициента мощности нередко указывают и нрав нагрузки: активно-ёмкостная либо активно-индуктивная. Тогда коэффициент мощности именуют соответственно опережающим либо отстающим.
Мощность в цепи переменного тока
Для начала следует тщательно разглядеть вопрос электрической мощности. В электрической цепи неизменного тока все очень просто и довольно понятно. В таковой цепи зная напряжение на зажимах потребителя и протекающий ток можем просто найти потребляемую мощность, умножив величину тока на напряжение:
В цепи переменного тока формулы для расчета мощности и само понятие мощности несколько труднее. В общем случае в электрической цепи синусоидального переменного тока изменение напряжения и тока во времени не совпадают. Либо другими словами напряжение и ток не совпадают по фазе. Ток отстает по фазе от напряжения при индуктивной нагрузке, и опережает напряжение при емкостной нагрузке. Исключительно в личном случае, когда нагрузка чисто активная, ток и напряжение совпадает по фазе. В сети переменного тока различают полную, активную и реактивную мощность. Отметим, что само понятие реактивной мощности животрепещуще только для электротехнических устройств переменного тока. Оно никогда не применяется к потребителям неизменного тока в силу малости (мизерности) соответственных эффектов, проявляющихся краткосрочно только при переходных процессах (включении/выключении, регулирование, изменение нагрузки).
Полная мощность в цепи переменного тока (для однофазовой нагрузки) равна произведению действующего значения тока на действующее значение напряжения (измеряется в ВА , кВА – вольт-амперах, кило вольт-амперах)
.
Полная мощность представляет практический энтузиазм, как величина, определяющая фактические электрические нагрузки на обмотки, провода, кабели, аппаратуру распределительных щитов, силовые трансформаторы, полосы электропередач. Фактически потому номинальная мощность генераторов и трансформаторов, нагрузки аппаратов распределительных щитов и пропускная способность линий электропередач указывается в вольт-амперах, а не в ваттах.
Полная мощность состоит из 2-ух составляющих – активной Р, и реактивной Q мощности. Активная мощность это та часть электроэнергии выработанной генератором, которая невозвратно преобразуется в термическую (лампы накаливания, электрической плиты, электропечи сопротивления, утраты в трансформаторах и линиях электропередачи) либо в механическую (электрические движки) энергию. Активная мощность измеряется в Вт, кВт (ватт, киловатт). Активную мощность можно найти по следующей формуле (для однофазовой нагрузки):
Вот тут и возникает именитый cos φ
.
Если ток совпадает по фазе с приложенным напряжением то угол φ = 0, и соответственно cos φ =1. Для электрической сети это сбалансированный вариант. В данном случае полная мощность равна активной мощности и вся электрическая энергия в нагрузке преобразуется в другие виды энергии. К примеру, в электрочайнике – в термическую энергию.
Почаще потребители электроэнергии имеют обмотки и магнитопроводы (электрические движки, трансформаторы, дроссели газорязрядных ламп, пускатели и реле) нужные для их обычной работы. В общем случае такая нагрузка именуется индуктивной. При чисто индуктивной нагрузке ток отстает от напряжения на угол φ = 90О , при котором cos φ = 0 и активная мощность также P = 0. Для свойства таких потребителей в электротехнике введено понятие реактивной мощности:
.
Реактивная мощность измеряется в Вар, кВАр (вольт-амперах реактивных, кило вольт-амперах реактивных). Кстати, реактивную мощность можно измерить при помощи счетчика реактивной энергии, также как и активную счетчиком активной энергии.
Названа мощность реактивной совершенно не по аналогии с «ракетой». Мы помним, что в физике термин «реактивный» обычно употребляется как связанный с появлением движения под действием силы отдачи струи пара, газа и т. п., вытекающей с большой скоростью в обратную силе отдачи сторону. В электротехнике это элемент электрической цепи, владеющий индуктивностью и/либо электрической ёмкостью, и термин реактивный употребляется для свойства элемента электрической цепи, владеющего этими качествами.
Источниками реактивной мощности в сети переменного тока являются катушки индуктивности и конденсаторы. На физическом уровне реактивная мощность, это мощность, которая скапливается в электрических и магнитных полях. При наличии в сети индуктивности и, к примеру, статического конденсатора электромагнитная энергия в один полупериод конфигурации тока скапливается в электромагнитном поле катушки индуктивности, в следующий полупериод ворачивается конденсатору, где скапливается в его электрическом поле, а потом ворачивается назад к индуктивности. Следует осознавать, что реактивная мощность не расходуется на выполнение работы электротехнического устройства (нагрев, выполнение механической работы) но она нужна для его обычной работы. Так в трансформаторе электрическая энергия передается с первичной обмотки во вторичную цепь средством электромагнитного поля, для сотворения которого и нужна реактивная мощность. Преобразование электроэнергии в асинхронном электродвигателе осуществляется с помощь такого же электромагнитного поля, и опять для его сотворения также нужна источник реактивной мощности. На генерацию активной мощности расходуются первичные энергоресурсы – газ, мазут, уголь, энергия ветра либо падающей воды. Так как каждые полпериода переменного тока скопленная в магнитном поле реактивная энергия отдается назад в источник (синхронный генератор, конденсатор) то в эталоне на генерацию реактивной мощности не нужна расход первичного энергоэлемента. Но при более глубочайшем рассмотрении оказывается, что реактивная энергия не такая уж безопасная. На генерацию реактивной мощности все- таки нужна расходовать некоторое количество первичного энергоэлемента для покрытия механических и электрических утрат в генераторах, диэлектрических утрат в конденсаторах. Не считая того при передаче реактивной энергии в линиях и трансформаторах появляются утраты на нагрев. Еще одна проблема заключается в том, что генерация и передача реактивной энергии просит роста установленной мощности генераторов, роста сечения проводов и мощности трансформаторов, т. е. связана с большенными экономическими затратами.
В энергетической системе источниками реактивной мощности могут быть синхронные генераторы, синхронные компенсаторы, перевозбужденные синхронные движки и конденсаторы. Решение о методе компенсации реактивной мощности всегда нужно принимать на базе технико–экономического анализа.
Большая часть потребителей электроэнергии имеют обмотки на магнитопроводах, т.е. представляют собой индуктивность. Чисто условно принято гласить, что они потребляют положительную реактивную мощность. Реактивная мощность статических конденсаторов отрицательна и принято гласить, что они генерируют реактивную мощность. Синхронные генераторы зависимо от величины тока возбуждения могут, как создавать, так и потреблять реактивную мощность. Т.е. ведут себя относительно электрической сети как емкость либо как индуктивность. То же можно сказать и о синхронных движках и синхронных компенсаторах. Вобщем, есть класс синхронных машин – реактивные машины, которые таковой способностью не владеют.
Численное значение коэффициента мощности электроустановок переменного тока может находится в спектре от 0,05-0,1 для трансформаторов в режиме холостого хода до 1,0 для нагревательных электроприборов и ламп накаливания. Коэффициент мощности асинхронных электродвигателей при номинальной нагрузке может быть 0,7 – 0,9 и находится в зависимости от номинальной мощности, конструктивного выполнения, также числа полюсов. Маломощные и тихоходные (многополюсные) движки отличаются пониженным значением cos φ . С уменьшением загрузки движков и трансформаторов их cos φ также существенно миниатюризируется.
Измерение коэффициента мощности
Для прямого измерения cos φ и фазы используются особые электроизмерительные приборы — фазометры.
При отсутствии таких устройств коэффициент мощности можно найти косвенным способом по свидетельствам 3-х устройств :амперметра, вольтметра и ваттметра. Тогда в однофазовой цепи
cos φ = P / (U х I),
где Р, U, I — показания ваттметра, вольтметра и амперметра, соответственно.
В симметричной трехфазной цепи
cos φ = Pw / (√3 х Uл х Iл);
где Pw – активная мощность трехфазной системы,
Uл, Iл – соответственно линейные напряжение и ток.
В симметричной трехфазной цепи значение коэффициента мощности можно найти также по свидетельствам 2-ух ваттметров Pw1 и Pw2 по формуле
Коэффициент мощности величина не неизменная, он находится в зависимости от нрава и величины нагрузки. Для асинхронного мотора изменение нагрузки от нуля до номинальной приводит к изменению cos φ от 0,1 на холостом ходу до 0,86 — 0,87 при номинальной нагрузке. Для практических целей расчета мощности компенсирующих устройств в электрических сетях применяют средневзвешенный коэффициент мощности за некоторый интервал времени — день либо месяц. Для этого за рассматриваемый период снимают показания счетчиков активной и реактивной энергии Wa и Wр и расчитывают средневзвешенный коэффициент мощности по формуле
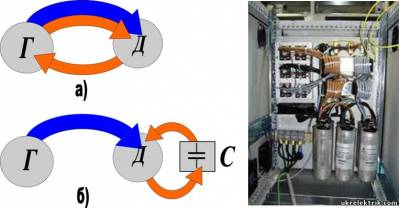
Компенсация реактивной мощности
Для уменьшения утрат, устранения перегрузок трансформаторов и линий электропередач прибегают к искусственному увеличению коэффициента мощности электрических установок методом компенсации реактивной мощности конкретно у потребителей при помощи батарей статических конденсаторов.
Энергетическая диаграмма, иллюстрирующая передачу электроэнергии между генератором Г и потребителем Д, потребляющим активную и реактивную энергию. а) — при отсутствии компенсатора, б) — при наличии его (батарея статических конденсаторов С) . Синим цветом показано поток активной энергии, красным – реактивной.
§57. Мощность переменного тока и коэффициент мощности
Секундное значение мощности. В цепи, содержащей активное, индуктивное и емкостное сопротивления, в какой ток I и напряжение u в общем случае смещены по фазе на некоторый угол ?, секундное значение мощности р равно произведению моментальных значений силы тока i и напряжения u. Кривую моментальной мощности р можно получить перемножением моментальных значений тока i и напряжения u при разных углах ?t (рис. 199, а. Из этого рисунка видно, что в некоторые моменты времени, когда ток и напряжение ориентированы навстречу друг дружке, мощность имеет отрицательное значение. Появление в электрической цепи отрицательных значений мощности является вредным. Это значит, что в такие периоды времени приемник возвращает часть приобретенной электроэнергии назад источнику; в итоге миниатюризируется мощность, передаваемая от источника к приемнику. Разумеется, что чем больше угол сдвига фаз ?, тем больше время, в течение которого часть электроэнергии ворачивается назад к источнику, и тем больше возвращаемая назад энергия и мощность.
Активная и реактивная мощности. Моментальная мощность может быть представлена в виде суммы 2-ух составляющих 1 и 2 (рис. 199,б). Составляющая 1 соответствует изменению мощности в цепи с активным сопротивлением (см. рис. 175,б).
Среднее ее значение, которое именуют активной мощностью,
P = UI cos ? (75)
Она представляет собой среднюю мощность, которая поступает от источника к электрическим установкам при переменном токе.
Составляющая 2 меняется подобно изменению мощности в цепи с реактивным сопротивлением (индуктивным либо емкостным, см. рис. 179, а и б). Среднее ее значение равно нулю, потому для оценки этой составляющей пользуются ее амплитудным значением, которое именуют реактивной мощностью:
Q = UI sin ? (76)
Рассматривая кривые мощности (см. рис. 199,б), можно установить, что только активная мощность может обеспечить преобразование в приемнике электроэнергии в другие виды энергии. Эта мощность в течение всего периода имеет положительный символ, т. е. соответственная ей электрическая энергия 2, именуемая активной, безпрерывно перебегает от источника 1 к приемнику 4 (рис. 200, а). Реактивная мощность никакой полезной работы сделать не может, так как среднее значение ее в течение 1-го периода равно нулю. Как видно из рис. 199,б, эта мощность становится то положительной, то отрицательной, т. е. соответственная ей электрическая энергия ,3, именуемая реактивной,
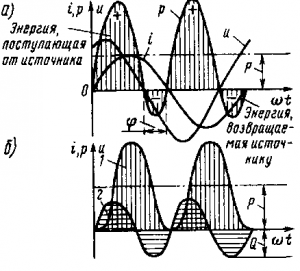
Рис. 199. Зависимость моментальной мощности р (а) и ее составляющих (б) от угла ?t
Рис. 200. Диаграмма, иллюстрирующая передачу электроэнергии между источником и приемником, содержащим активное и реактивное сопротивления, при отсутствии компенсатора (а) и при наличии его (б): 1 — источник; 2,3 — условные изображения активной и реактивной энергии; 4 — приемник; 5 — компенсатор
безпрерывно циркулирует по электрической цепи от источника электроэнергии 1 к приемнику 4 и назад (см. рис. 200, а).
Появление реактивной мощности в цепи переменного тока может быть только при включении в эту цепь накопителей энергии, таких как катушка индуктивности либо конденсатор. В первом случае электрическая энергия, поступающая от источника, скапливается в электромагнитном поле катушки индуктивности, а потом отдается назад; во 2-м случае она скапливается в электрическом поле конденсатора, а потом ворачивается назад к источнику. Неизменная циркуляция реактивной мощности от источника к приемникам загружает генераторы переменного тока и электрические сети реактивными токами, не создающими полезной работы, и тем не дает способности применять их по прямому предназначению для выработки и передачи потребителям активной мощности. Потому в производственных критериях стараются по способности уменьшить реактивную мощность, потребляемую электрическими установками.
Полная мощность. Источники электроэнергии переменного тока (генераторы и трансформаторы) рассчитаны на определенный номинальный ток Iном и определенное номинальное напряжение Uном, которые зависят от конструкции машины, размеров ее главных частей и пр. Прирастить существенно номинальный ток либо номинальное напряжение нельзя, так как это может привести к недопустимому нагреву обмоток машины либо пробою их изоляции. Потому каждый генератор либо трансформатор может продолжительно отдавать без угрозы трагедии только полностью определенную мощность, равную произведению его номинального тока на номинальное напряжение. Произведение действующих значений тока и напряжения именуется полной мощностью,
Поэтому, полная мощность представляет собой наибольшее значение активной мощности при данных значениях тока и напряжения. Она охарактеризовывает ту самую большую мощность, которую можно получить от источника переменного тока при условии, что между проходящим по нему током и напряжением отсутствует сдвиг фаз. Полную мощность определяют в вольт-амперах (В*А) либо киловольт-амперах (кВ*А).
Связь между мощностями Р, Q и S можно найти из векторной диаграммы напряжений (рис. 201, а). Если помножить на ток I все стороны треугольника ABC, то получим треугольник мощностей А’В’С’ (рис. 201,б), стороны которого равны Р, Q и S. Из треугольника мощностей имеем:
Из этого выражения следует, что при данной полной мощности S (т. е. напряжении U и токе I) чем больше реактивная мощность Q, которая проходит через генератор переменного тока либо трансформатор, тем меньше активная мощность Р, которую он может дать приемнику. Другими словами, реактивная мощность не позволяет вполне применять всю расчетную мощность источников переменного тока для выработки полезно применяемой электроэнергии. То же самое относится и к электрическим сетям. Ток I = ?(Ia 2 +Ip 2 ), который можно неопасно пропускать по данной электрической сети, определяется, приемущественно, поперечным сечением ее проводов. Потому если часть Iр проходящего по сети тока (см. рис. 194,б) идет на создание реактивной мощности, то должен быть уменьшен активный ток Iа, обеспечивающий создание активной мощности, которую можно пропустить по данной сети.
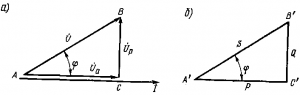
Рис. 201. Векторная диаграмма напряжений (а) и треугольник мощностей (б) для цепи переменного тока
Если задана активная мощность Р, то при увеличении реактивной мощности Q вырастут реактивный ток Iр и общий ток I, проходящий по проводам генераторов переменного тока, трансформаторов, электрических сетей и приемников электроэнергии. При всем этом растут и утраты мощности ?Р = I 2 Rпp в активном сопротивлении Rпp этих проводов.
Таким макаром, никчемная циркуляция электроэнергии между источником переменного тока и приемником, обусловленная наличием в нем реактивных сопротивлений, просит также издержки определенного количества энергии, которая пропадает в проводах всей электрической цепи.
Коэффициент мощности. Из формулы (75) следует, что активная мощность Р зависит не только лишь от тока I и напряжения U, но и от величины cos?, именуемой коэффициентом мощности:
cos ? = P/(UI) = P/S = P/?(P 2 + Q 2 )
По значению cos ? можно судить, как употребляет мощность источника данный приемник либо электрическая цепь. Чем больше cos ?, тем меньше sin ?, поэтому, согласно формулам (75) и (76) при данных U и I, т. е. S, тем больше активная и меньше реактивная мощности, отдаваемые источником. При повышении cos ? и неизменной активной мощности Р, поступающей в приемник, миниатюризируется ток в цепи I = P/(U cos ?). При всем этом уменьшаются утраты мощности ?P = I 2 Rпp в проводах и обеспечивается возможность дополнительной загрузки источника и электрической сети, т. е. наилучшего их применения. Если приемник питается от источника при постоянном токе нагрузки, то увеличение cos ? ведет к возрастанию активной мощности Р, применяемой приемником. При cos?=1 реактивная мощность равна нулю, и вся мощность, отдаваемая источником, является активной. Потому на всех предприятиях и во всех отраслях народного хозяйства стремятся всемерно увеличивать коэффициент мощности и доводить его по способности до единицы.
Значения коэффициента мощности электрических установок переменного тока различны. Электрические лампы владеют, приемущественно, активным сопротивлением, потому при их включении сдвиг фаз между током и напряжением фактически отсутствует. Поэтому, для осветительной нагрузки коэффициент мощности можно считать равным единице. Коэффициент мощности для движков переменного тока находится в зависимости от нагрузки. При номинальной расчетной нагрузке мотора cos? = 0,8-0,9, а у больших движков даже выше. При недогрузке движков коэффициент мощности их резко понижается (при холостом ходе cos ? = 0,25-0,3).
Увеличение коэффициента мощности. Cos ? увеличивают разными методами. Основной из них — включение параллельно приемникам электроэнергии особых устройств, именуемых компенсаторами. В качестве последних в большинстве случаев применяют батареи конденсаторов (статические компенсаторы), но могут быть использованы также и синхронные электрические машины (крутящиеся компенсаторы).
Метод увеличения cos ? при помощи статического компенсатора (рис. 202, а) именуют компенсацией сдвига фаз, либо компенсацией реактивной мощности. При отсутствии компенсатора от источника к приемнику, содержащему активное и индуктивное сопротивления, поступает ток i1 который отстает от напряжения и на некоторый угол сдвига фаз ?1. При включении компенсатора Хс по нему проходит ток ic, опережающий напряжение и на 90°. Как видно из векторной диаграммы (рис. 202,б), при всем этом в цепи источника будет перейти ток i<i1 и угол сдвига фаз его ? относительно напряжения также будет меньше ?1.
Для полной компенсации угла сдвига фаз ?, т. е. для получения cos ? =1 и малого значения тока Imin, нужно, дабы ток компенсатора Iс был равен реактивной составляющей I1p = I1 sin ?1 тока I1.
При включении компенсатора 5 (см. рис. 200,б) источник 1 и электрическая сеть разгружаются от реактивной энергии 3, так как она циркулирует уже по цепи «приемник — компенсатор». Благодаря этому достигаются существенное увеличение применения генераторов переменного тока и электрических сетей и уменьшение утрат энергии, возникающих при никчемной циркуляции реактивной энергии между источником 1 и приемником 4. Компен-
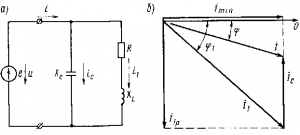
Рис. 202. Схема, иллюстрирующая метод увеличения cos ? при помощи компенсатора (а), и векторная диаграмма (б)
сатор в данном случае играет роль генератора реактивной энергии, так как токи Iсв конденсаторе и I1р в катушке индуктивности (см, рис. 202,б) ориентированы навстречу один другому (1-ый опережает по фазе напряжение на 90°, 2-ой отстает от него на 90°), вследствие чего включение компенсатора уменьшает общий реактивный ток Iр и сдвиг фаз между током I и напряжением U. При соответствующем подборе реактивной мощности компенсатора можно достигнуть, что вся реактивная энергия 3 (см. рис. 200,б), поступающая в приемник 4, будет циркулировать снутри контура «приемник — компенсатор», а генератор и сеть не будут участвовать в ее передаче. При этих критериях от источника 1 к приемнику 4 будет передаваться только активная мощность 2, т. е. cos ? будет равен единице.
Почти всегда по экономическим суждениям в электрических установках производят неполную компенсацию угла сдвига фаз и ограничиваются значением cos ? = 0,95.






