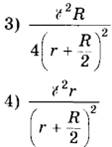Номинальная мощность резистора определяет, какое наибольшее количество энергии может рассеять резистор без риска перегрева.
Закон Ома для участка цепи утверждает что, электрическая мощность связана с напряжением и током:
Если электрическая мощность, выделяемая на резисторе, не превосходит его номинальную рассеиваемую мощность, температура резистора будет размеренной. Необходимо подчеркнуть, что температура на самом резисторе распределена не умеренно. Его корпус мало теплее, чем выводы, а самая высочайшая температура в центре корпуса.
Магнитный держатель печатной платы
Крепкая железная база с порошковым покрытием, четыре гибкие руч.
Чем выше скорость теплопотери в окружающую среду, тем ниже температура на резисторе. Большие резисторы с большой площадью поверхности, обычно, могут рассеивать существенное количество термический мощности.
Если мощность выделяемая на резисторе превосходит его номинальную мощность, то резистор может быть поврежден. Это может иметь несколько последствий:
- изменение значения сопротивления,
- понижение срока службы,
- полный выход из строя в итоге обрыва цепи,
- в экстремальных случаях чрезмерная мощность может даже стать предпосылкой возгорания.
Определение: мощность резистора — номинальная мощность, которую может рассеять резистор, сохраняя при всем этом свою работоспособность.
Мощность резистора
Номинальная мощность резистора определяется для определенной температуры окружающей среды на открытом воздухе. Направьте внимание, что на практике количество энергии, которую резистор может рассеять без повреждения сильно находится в зависимости от критерий эксплуатации и, поэтому, не равна номинальной мощности.
К примеру, увеличение температуры окружающей среды может существенно уменьшить номинальную мощность резистора.
Это следует учесть при разработке схем. Обычно резисторы рассчитаны для работы при температуре до 70°С, выше этого значения резистор существенно понижает свою номинальную рассеиваемую мощность. Это иллюстрируется кривой ухудшения характеристик.
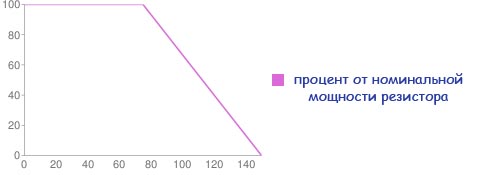
Вместе с воздействием температуры окружающей среды, еще есть несколько причин, влияющих на изменение номинального значения мощности резистора. Более принципиальные причины приведены ниже:
Корпус
Скорость теплопотери ограничивается из-за установки резистора в корпус устройства. Корпус ограничивает воздушный поток и, поэтому, отвод тепла методом конвекции. Излучаемое тепло будет удаляться неэффективно, так как стены корпуса действуют как термический барьер. Воздействие корпуса на степень утраты тепла сильно находится в зависимости от размера, формы, материала и толщины стен.
Принудительное остывание
Повышение теплопередачи средством принудительной конвекции позволяет получить более высшую рассеиваемую мощность, чем методом обыкновенной естественной конвекции.
Это может быть достигнуто методом сотворения воздушного потока, либо даже жидкостным остыванием. Некоторые массивные резисторы имеют ребристый корпус, дабы сделать огромную поверхность для рассеивания тепла.
Группировка компонент
На печатной плате резисторы часто размещены близко друг к другу. В таком случае термическое излучение 1-го резистора будет влиять на показатель мощности вблизи расположенных резисторов.
В заключении хотелось бы отметить, что для большинства электронных схем номинальная мощность резисторов не является главным параметром, так как эти резисторы рассеивают маленькое количество энергии от 1-го ватта и меньше.
Но в силовой электронике мощность является принципиальной чертой. Обычной областью использования массивных резисторов являются источники питания, динамические тормоза, преобразователи мощности, усилители и нагреватели.
§ 107. Примеры решения задач по теме «Работа и мощность неизменного тока. Закон Ома для полной цепи»
При решении задач, связанных с расчётом работы и мощности тока, нужно использовать формулы (15.13) и (15.15).
Для определения силы тока в замкнутой цепи нужно применять закон Ома для полной цепи, а в случае нескольких источников верно найти суммарную ЭДС.
Задачка 1. Аккумулятор с ЭДС Ε = 6,0 В и внутренним сопротивлением r — 0,1 Ом питает внешнюю цепь с сопротивлением R = 12,4 Ом. Какое количество теплоты Q выделится во всей цепи за время t = 10 мин?
Р е ш е н и е. Согласно закону Ома для замкнутой цепи сила тока в цепи равна Количество теплоты, выделившейся на наружном участке цепи, Q1 = I 2 Rt, на внутреннем — Q2 = I 2 rt. Общее количество теплоты
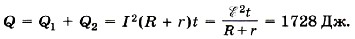
Задачка 2. Разность потенциалов в сети зарядной станции равна 20 В. Внутреннее сопротивление аккума, поставленного на зарядку, равно 0,8 Ом; в исходный момент времени его остаточная ЭДС равна 12 В. Какая мощность будет расходоваться станцией на зарядку аккума при этих критериях? Какая часть этой мощности будет расходоваться на нагревание аккума?
Р е ш е н и е. При зарядке аккума зарядное устройство и аккумулятор соединены разноимёнными полюсами навстречу друг дружке. Сила тока, идущего через аккумулятор, I = (U — Ε)/R. Мощность, используемая станцией:
Мощность, используемая на нагревание аккума:
Задачка 3. При подключении вольтметра сопротивлением RV = 200 Ом конкретно к зажимам источника он указывает U = 20 В. Если же этот источник замкнуть на резистор сопротивлением R = 8 Ом, то сила тока в цепи I2 = 0,5 А. Обусловьте ЭДС и внутреннее сопротивление источника.
Р е ш е н и е. По закону Ома для полной цепи в первом случае сила тока во 2-м случае Показания вольтметра — падение напряжения на его внутреннем сопротивлении, т. е. U = I1RV. Из соотношения I1(RV + r) = I2(R + r) найдём внутреннее сопротивление источника:
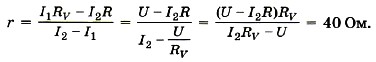
Для ЭДС источника запишем: Ε = I2(R + r) = 24 В.
Задачка 4. Обусловьте силу тока недлинного замыкания для источника, который при силе тока в цепи I1 = 10 А имеет полезную мощность Р1 = 500 Вт, а при силе тока I2 = 5 А — мощность Р2 = 375 Вт.
Р е ш е н и е. Сила тока недлинного замыкания Нужная мощность Р = IU, где U — напряжение на зажимах источника, либо падение напряжения на наружном участке цепи. Напряжения на зажимах источника в первом и во 2-м случаях
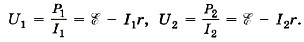
Вычтем почленно из первого выражения 2-ое:
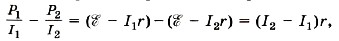
откуда определим
ЭДС источника тока
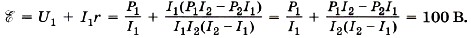
Совсем для силы тока недлинного замыкания
Задачка 5. Конденсатор ёмкостью 2 мкФ включён в цепь (рис. 15.12), содержащую три резистора и источник неизменного тока с ЭДС 3,6 В и внутренним сопротивлением 1 Ом. Сопротивления резисторов R1 = 4 Ом, R2 = 7 Ом, R3 = 3 Ом. Чему равен заряд на правой обкладке конденсатора?
Р е ш е н и е. Участок цепи, в каком находится конденсатор, разомкнут, и ток через резистор R3 не идёт.
Разность потенциалов между пластинами конденсатора равна падению напряжения на резисторе R2: U = IR2.
Сила тока, идущего по цепи, согласно закону Ома равна
Заряд на обкладках конденсатора
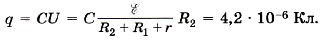
На правой обкладке конденсатора накопится отрицательный заряд, так как она подключена к отрицательному полюсу источника.
Задачка 6. Обусловьте характеристики источника тока, если понятно, что наибольшая мощность, равная 40 Вт, выделяется при подключении резистора сопротивлением 10 Ом.
Р е ш е н и е. Наибольшая мощность выделяется при равенстве наружного и внутреннего сопротивлений, поэтому, R = r = 10 Ом.
Мощность определяется формулой Р = I 2 R, либо с учётом закона Ома:
Тогда ЭДС источника
Задачи для самостоятельного решения
1. За некоторый промежуток времени электрическая плитка, включённая в сеть с неизменным напряжением, выделила количество теплоты Q. Какое количество теплоты выделят за то же время две такие плитки, включённые в ту же сеть последовательно? параллельно? Изменение сопротивления спирали зависимо от температуры не учесть.
2. Чему равно напряжение на клеммах гальванического элемента с ЭДС, равной Ε, если цепь разомкнута?
3. Чему равна сила тока при маленьком замыкании аккума с ЭДС Ε = 12 В и внутренним сопротивлением r = 0,01 Ом?
4. Батарейка для карманного фонаря замкнута на резистор переменного сопротивления. При сопротивлении резистора, равном 1,65 Ом, напряжение на нём равно 3,30 В, а при сопротивлении, равном 3,50 Ом, напряжение равно 3,50 В. Обусловьте ЭДС и внутреннее сопротивление батарейки.
5. Источники тока с ЭДС 4,50 В и 1,50 В и внутренними сопротивлениями 1,50 Ом и 0,50 Ом, соединённые, как показано на рисунке (15.13), питают лампу от карманного фонаря. Какую мощность потребляет лампа, если понятно, что сопротивление её нити в нагретом состоянии равно 23 Ом?
6. Замкнутая цепь питается от источника с ЭДС Ε = 6 В и внутренним сопротивлением 0,1 Ом. Постройте графики зависимости силы тока в цепи, напряжения на зажимах источника и мощности от сопротивления наружного участка.
7. Два элемента, имеющие однообразные ЭДС по 4,1 В и однообразные внутренние сопротивления по 4 Ом, соединены одноимёнными полюсами, от которых изготовлены выводы, так что вышла батарейка. Какую ЭДС и какое внутреннее сопротивление обязан иметь элемент, которым можно было бы поменять такую батарейку?
Эталоны заданий ЕГЭ
C1. Резисторы поочерёдно подключают к источнику неизменного тока. Сопротивления резисторов равны соответственно 3 Ом и 12 Ом. Мощность тока в резисторах одинакова. Чему равно внутреннее сопротивление источника тока?
C2. ЭДС источника неизменного тока Ε = 2 В, а его внутреннее сопротивление r = 1 Ом. Мощность тока в резисторе, подключённом к источнику, Р0 = 0,75 Вт. Чему равна сила тока в цепи?
C3. Электрическая цепь состоит из источника тока и реостата. ЭДС источника б В, его внутреннее сопротивление r = 2 Ом. Сопротивление реостата можно изменять в границах от 1 до 5 Ом. Чему равна наибольшая мощность, выделяемая на реостате?
C4. К однородному медному цилиндрическому проводнику длиной 10 м приложили разность потенциалов 1 В. Обусловьте промежуток времени, в течение которого температура проводника повысится на 10 К. Конфигурацией сопротивления проводника и рассеянием тепла при его нагревании можно пренебречь. Плотность меди 8900 кг/м 3 , удельное сопротивление меди 1,7 • 10 -8 Ом • м, удельная теплоёмкость меди 380 Дж/(кг • К).
Повторите материал главы 15 по следующему плану
1. Выпишите главные понятия и физические величины и дайте им определение.
2. Сформулируйте законы и запишите главные формулы.
3. Укажите единицы физических величин и их выражение через главные единицы СИ.
4. Опишите главные опыты, подтверждающие справедливость законов.
«Источники неизменного тока и их применение»
1. 1-ые источники тока — хим источники.
2. Фотоэлектрический эффект. Фотоэлементы.
3. Термоэлектрический эффект. Термоэлементы.
«Экспериментальная проверка закона Ома для полной цепи»
«Создание экспериментальной установки для исследования термических действий тока»
Задание 31 ЕГЭ по физике
Обычно это задание по теме «Электродинамика». Оно просит умения читать электрические схемы и использовать теоретические познания при решении задач. На каждом шаге нужно проводить анализ выведенных формул, вводить дополнительные обоснования в процессе решения. Так как это задание высокого уровня трудности, то в них могут появляться ситуации, которые не встречались ранее в сборниках задач.
1. К аккуму с ЭДС 50 В и внутренним сопротивлением 4 Ом подключили лампу сопротивлением 10 Ом и резистор сопротивлением 15 Ом, также конденсатор ёмкостью 100 мкФ (см. набросок). Спустя долгий промежуток времени ключ К размыкают. Какое количество теплоты выделится после чего на лампе?
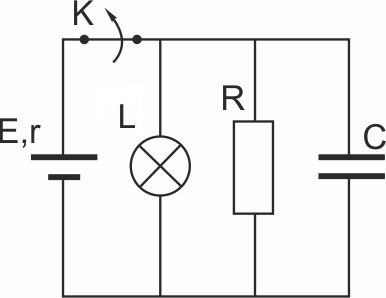
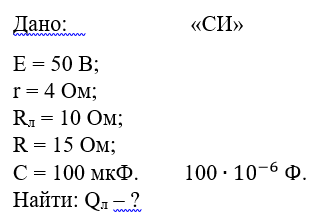
До размыкания ключа электрический ток протекает через параллельно соединённые лампу и резистор. Найдем их общее сопротивление.
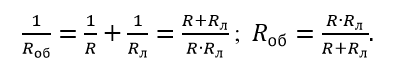
Проведем расчет общего сопротивления.
По закону Ома для полной цепи определим общую силу тока.
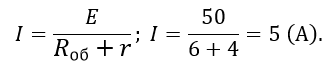
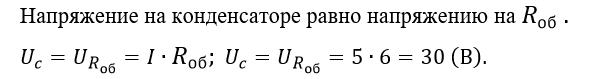
Таким макаром, до размыкания ключа в конденсаторе была накоплена энергия (Дж) = 45 (мДж).
После размыкания ключа вся энергия, скопленная в конденсаторе, будет выделяться на параллельно включенных лампе и резисторе. Согласно закону Джоуля – Ленца, количество теплоты, выделяющееся в промежуток времени назад пропорционально сопротивлению, так как напряжение u на лампе и резисторе в хоть какой момент времени одно и то же.

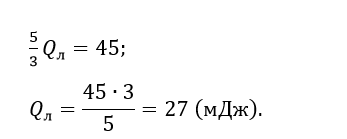
Секрет решения. Осознание схемы является ключом к решению данной задачи. Так как конденсатор заряжен, то после размыкания ключа происходит рассредотачивание накопившейся энергии между лампочкой и сопротивлением. С учетом того, что лампочка и резистор соединены параллельно, тут нужна формула Если б они были соединены последовательно, то было надо воспользоваться формулой Выбор формулы определяется видом соединения и всепостоянством или напряжения, или силы тока. Задачку удобнее решать, проводя промежные вычисления.
2. На рисунке показана схема электрической цепи, состоящей из источника тока с ЭДС mathcal E=12 В и внутренним сопротивлением r = 1 Ом, 2-ух резисторов с сопротивлениями Ом и Ом, конденсатора электроёмкостью С = 4 мкФ и катушки с индуктивностью L = 24 мкГн. В исходном состоянии ключ К долгое время замкнут. Какое количество теплоты выделится на резисторе R_ после размыкания ключа К? Сопротивлением катушки пренебречь.
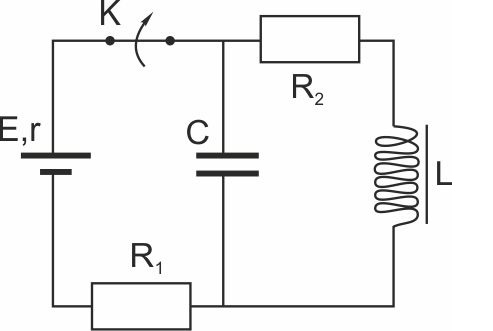
До размыкания ключа электрический ток протекает через последовательно соединённые резисторы и катушку L.
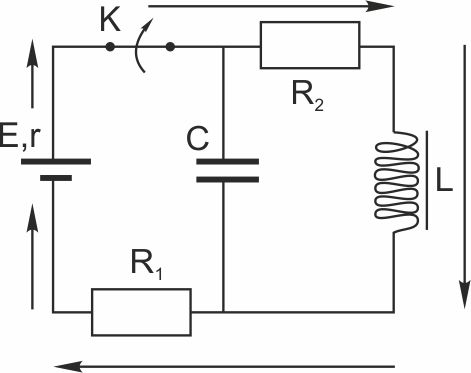
Направление тока I на схеме обозначено стрелками.
По закону Ома для полной цепи можно найти значение силы тока.
Проведем расчет значения силы тока.
(А).
Так как конденсатор соединен наряду с резистором то напряжения у них будут одинаковыми.
– напряжение на конденсаторе, – напряжение на резисторе
По закону Ома для участка цепи можно записать, что
(В).
(В).
Таким макаром, до размыкания ключа в конденсаторе была накоплена энергия (Дж)=18 (мкДж).
В катушке индуктивности скапливается энергия магнитного поля, которую можно высчитать по формуле:
(Дж)=12 (мкДж).
После размыкания ключа вся скопленная в элементах цепи энергия выделится в виде тепла на резисторе
Секрет решения. Умение читать электрические схемы является ключом к решению схожих задач. Становится естественным, что конденсатор и резистор соединены параллельно, их напряжения однообразные, при всем этом ток через конденсатор не протекает. Место между пластинами конденсатора разбито слоем диэлектрика, потому на пластинках скапливается электрический заряд, но ток через него не течет.
При протекании тока через катушку в ней скапливается энергия магнитного поля. При всем этом нужно осознавать, что сопротивление катушки не оказывает влияние на значение тока в цепи, оно по условию равно нулю. Соответственно, напряжение на концах катушки по закону Ома также равно нулю.
После размыкания ключа скопленные энергии (электрического и магнитного полей) выделяются в виде тепла на резисторе
3. В цепи, изображённой на рисунке, сопротивление диодика
в прямом направлении пренебрежимо не достаточно, а в оборотном неоднократно превосходит сопротивление резисторов. При подключении к точке А положительного полюса, а к точке В отрицательного полюса батареи с ЭДС 12 В и пренебрежимо малым внутренним сопротивлением, потребляемая мощность равна 14,4 Вт. При изменении полярности подключения батареи потребляемая мощность оказалась
равной 21,6 Вт. Укажите, как течёт ток через диодик и резисторы в обоих случаях, и обусловьте сопротивления резисторов в этой цепи.
Если при подключении батареи потенциал точки А оказывается выше, чем потенциал точки В, то ток через диодик не течёт, и эквивалентная схема цепи имеет вид, изображённый на рис. 1. Потребляемую мощность можно высчитать по формуле:
Проведем расчет для
При изменении полярности подключения батареи диодик раскрывается и подключает резистор параллельно резистору Эквивалентная схема цепи в данном случае изображена на рис. 2.
При всем этом потребляемая мощность возрастает:
(2). Эта формула для расчета мощности с учетом того, что резисторы и во 2-м случае соединены параллельно. Общая мощность, выделяемая в цепи, равна сумме мощностей на каждом из резисторов.
Выразим из формулы (2) сопротивление резистора
Подставим численные значения и проведем расчет.
Ответ: 20 Ом, 10 Ом.
Секрет решения. В этой задачке может появиться сложность с осознанием и механизмом работы диодика. Для решения задач, встречающихся в ЕГЭ по физике, не нужна глубочайших познаний по устройству этого полупроводникового устройства. Довольно знать, что диодик обладает однобокой проводимостью. На схемах направление пропускания тока обозначено стрелкой. При оборотном подключении диодик закрыт, другими словами ток через него не течет.
В остальном задачка является стандартной и базируется на узнаваемых закономерностях. Если формула (2) явна не сходу, то общую мощность, выделяемую в цепи, можно разглядеть, как мощность на сопротивлении Rобщ, а его можно высчитать по формуле:
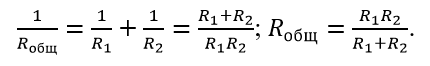
Тогда, общая мощность для второго варианта будет равна:
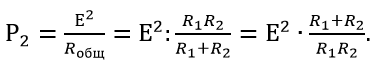
Используя приобретенное значение для из последней формулы можно вычислить сопротивление резистора