I- сила тока в цепи; Е- электродвижущая сила источника тока, включённого в цепь; R- сопротивление наружной цепи; r- внутреннее сопротивление источника тока.
МОЩНОСТЬ, ВЫДЕЛЯЕМАЯ ВО Наружной ЦЕПИ
. (2)
Из формулы (2) видно, что при маленьком замыкании цепи (R®0) и при R® эта мощность равна нулю. При всех других конечных значениях R мощность Р1> 0. Поэтому, функция Р1 имеет максимум. Значение R0, соответственное наибольшей мощности, можно получить, дифференцируя Р1 по R и приравнивая первую производную к нулю:
. (3)
Из формулы (3), с учётом того, что R и r всегда положительны, а Е ? 0, после легких алгебраических преобразований получим:
Поэтому, мощность, выделяемая во наружной цепи, добивается большего значения при сопротивлении наружной цепи равном внутреннему сопротивлению источника тока.
При всем этом сила тока в цепи (5)
равна половине тока недлинного замыкания. При всем этом мощность, выделяемая во наружной цепи, добивается собственного наибольшего значения, равного
. (6)
Когда источник замкнут на наружное сопротивление, то ток протекает и снутри источника и при всем этом на внутреннем сопротивлении источника выделяется некоторое количество тепла. Мощность, затрачиваемая на выделение этого тепла равна
. (7)
Поэтому, полная мощность, выделяемая во всей цепи , обусловится формулой
= I 2 (R+r) = IE (8)
КОЭФФИЦИЕНТ ПОЛЕЗНОГО Деяния
КОЭФФИЦИЕНТ ПОЛЕЗНОГО Деяния источника тока равен . (9)
Из формулы (8) следует, что
, (10)
т.е. Р1 меняется с конфигурацией силы тока в цепи по параболическому закону и воспринимает нулевые значения при I = 0 и при . 1-ое значение соответствует разомкнутой цепи ( R>> r ), 2-ое – недлинному замыканию ( R<< r). Зависимость к.п.д. от силы тока в цепи с учётом формул (8), (9), (10) воспримет вид
(11)
Таким макаром, к.п.д. добивается большего значения h =1 в случае разомкнутой цепи ( I = 0), а потом миниатюризируется по линейному закону, обращаясь в нуль при маленьком замыкании.
Зависимость мощностей Р1, Рполн = EI и к.п.д. источника тока от силы тока в цепи показаны на рис.1.
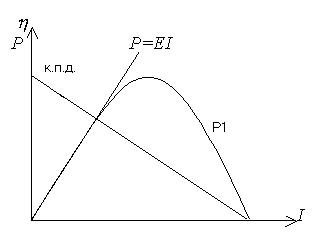
Из графиков видно, что получить сразу полезную мощность и к.п.д. нереально. Когда мощность, выделяемая на наружном участке цепи Р1, добивается большего значения, к.п.д. в этот момент равен 50%.
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ
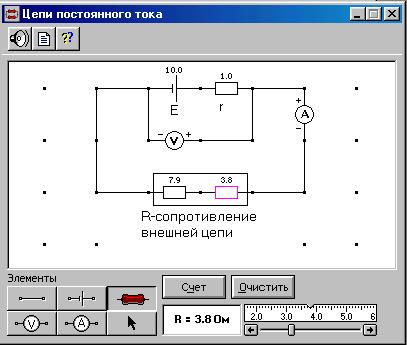
Соберите на дисплее цепь, показанную на рис. 2. Для этого поначалу щелкните левой кнопкой мыши над кнопкой э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где размещены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет размещен источник э.д.с.
Разместите дальше последовательно с источником резистор, изображающий его внутреннее сопротивление (нажав за ранее кнопку в нижней части экрана) и амперметр (кнопка там же). Потом расположите аналогичным образом резисторы нагрузки и вольтметр , измеряющий напряжение на нагрузке.
Подключите соединительные провода. Для этого нажмите кнопку провода понизу экрана, после этого переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода.
4. Установите значения характеристик для каждого элемента. Для этого щелкните левой кнопкой мыши на кнопке со стрелкой . Потом щелкните на данном элементе. Подведите маркер мыши к движку показавшегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашего варианта.
§ 32. Активное сопротивление. Действующие значения силы тока и напряжения
Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, присоединенной к источнику переменного напряжения.
Сила тока в цепи с резистором. Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и огромным сопротивлением R (рис. 4.10). Данную величину, которую мы до сего времени называли электрическим сопротивлением либо просто сопротивлением, сейчас будем именовать активным сопротивлением.
Сопротивление R именуется активным, так как при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия преобразуется во внутреннюю энергию проводников — они греются. Будем считать, что напряжение на зажимах цепи изменяется по гармоническому закону:
Как и в случае неизменного тока, секундное значение силы тока прямо пропорционально моментальному значению напряжения. Потому для нахождения моментального значения силы тока можно применить закон Ома:

В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряжения (рис. 4.11), а амплитуда силы тока определяется равенством

Мощность в цепи с резистором. В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение меняются сравнимо стремительно. Потому при прохождении тока по проводнику, к примеру по нити электрической лампочки, количество выделенной энергии также будет стремительно изменяться с течением времени. Но этих стремительных изменений мы не замечаем.
Обычно, нам необходимо бывает знать среднюю мощность тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого довольно отыскать среднюю мощность за один период. Под средней за период мощностью переменного тока понимают отношение суммарной энергии, поступающей в цепь за период, к периоду.
Мощность в цепи неизменного тока на участке с сопротивлением R определяется формулой
В протяжении очень малого интервала времени переменный ток можно считать фактически неизменным. Потому моментальная мощность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой
Найдем среднее значение мощности за период. Для этого поначалу преобразуем формулу (4.19), подставляя в нее выражение (4.16) для силы тока и используя известное из арифметики соотношение
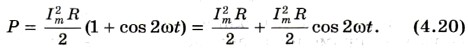
График зависимости моментальной мощности от времени изображен на рисунке 4.12, а. Согласно графику (рис. 4.12, б), в протяжении одной восьмой периода, когда cos 2ωt > 0, мощность в хоть какой момент времени больше, чем Зато в протяжении следующей восьмой части периода, когда cos 2ωt < 0, мощность в хоть какой момент времени меньше, чем Среднее за период значение cos 2ωt равно нулю, а означает равно нулю 2-ое слагаемое в уравнении (4.20).
Средняя мощность равна, таким макаром, первому члену в формуле (4.20):

Действующие значения силы тока и напряжения. Из формулы (4.21) видно, что величина есть среднее за период значение квадрата силы тока:

Величина, равная квадратному корню из среднего значения квадрата силы тока, именуется действующим значением силы переменного тока. Действующее значение силы переменного тока обозначается через I:

Действующее значение силы переменного тока равно силе такового неизменного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.
Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:

Заменяя в формуле (4.17) амплитудные значения силы тока и напряжения на их действующие значения, получаем

Это закон Ома для участка цепи переменного тока с резистором.
Как и при механических колебаниях, в случае электрических колебаний обычно нас не заинтересовывают значения силы тока, напряжения и других величин в каждый момент времени. Важны общие свойства колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Конкретно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.
Не считая того, действующие значения удобнее моментальных значений к тому же так как конкретно они конкретно определяют среднее значение мощности Р переменного тока:
Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.
Вопросы к параграфу
1. Чему равна амплитуда напряжения в осветительных сетях переменного тока, рассчитанных на напряжение 220 В?





