Решил как-то отец собрать для дачи некое устройство, в каком, по его заверению, можно будет варить сыр. Устройство сие вид имело могучий и представляло из себя металлический короб, подозрительно напоминающий старенькую стиральную машинку. Вовнутрь короба (все также качественно!) были вмонтированы три тэна по 1700 Ватт каждый. В общем сыра должно было хватить на маленький посёлок.
Изделие (снаружи выглядящее как что-то из сумасшедшего макса), должно быть очень технологичным и поддерживать заданную температуру в очень узеньких границах. Для этого вблизи появилась ещё одна коробка с симисторами, к которым подключались ТЭНы и схема, выдающая высочайший уровень при переходе синусоиды через ноль. А у меня появился увлекательный проект.
Итак нам необходимо выходить на заданную температуру и поддерживать её, с этим должен управляться метод ПИД регулятора. Глубоко вдаваться в его работу не буду, скажу только что он получает на вход текущую ошибку, а на выходе выдает какое-то число в данных границах. У меня таким числом будет мощность выдаваемая на ТЭН, хотя в принципе, это может быть хоть какой инерционный процесс, к примеру обороты мотора. Что принципиально для ПИД регулятора, это дабы выходная величина производила воздействие линейно. Потому попробуем разобраться в методах регулировки мощности и их линейности.
Как вообщем регулируется мощность?
Мощность — это произведение силы тока на напряжение. Если представить это произведение графически, то для неизменного тока, это будет площадь прямоугольника со сторонами равными напряжению и току
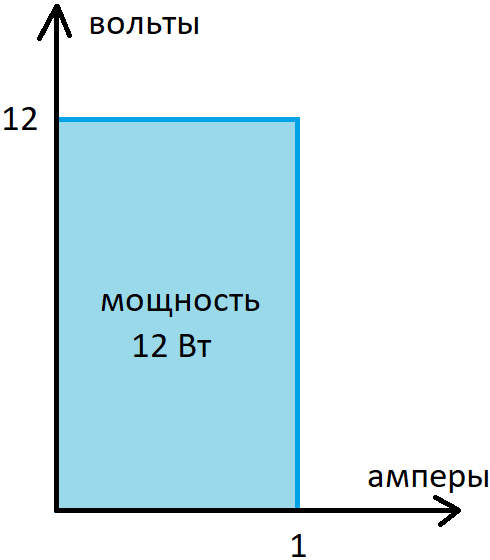
Так как при неизменном сопротивлении и напряжении ток тоже будет неизменным, то заменим ось тока на ось времени. Сопротивление я беру неизменным для разъяснения принципа регулирования.
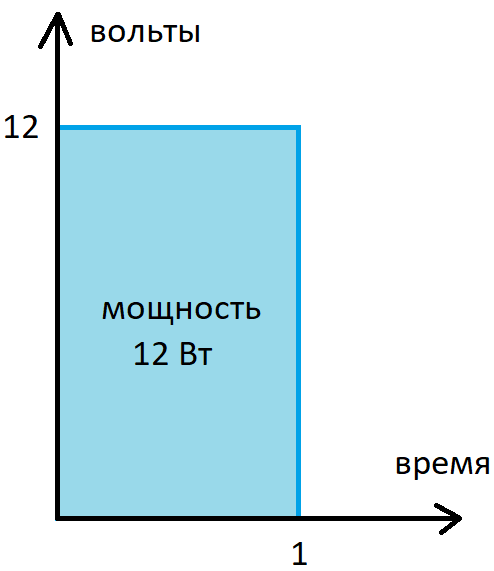
Тогда при данном напряжении (12 В) и сопротивлении в 12 Ом, по закону Ома: I=U/R, получаем ток равный 1 А, и соответственно мощность за единицу времени будет равна 12 Вт. При другом сопротивлении мощность, естественно тоже поменяется.
Сейчас, если мы желаем регулировать мощность за единицу времени, нам необходимо как-то изменять площадь фигуры за единицу времени. Самым незапятнанным методом будет просто изменять напряжение, и тогда мощность будет пропорционально изменяться. Но контроллер, как и любые цифровые устройства, не умеет плавненько изменять напряжение на ножках, он может или "подымать" их до высокого уровня, или "опускать" до малого уровня. Этот недочет он компенсирует скоростью, даже самый дохленький современный МК может работать на частотах в миллионы тактов за секунду. Дабы регулировать мощность, контроллер будет очень стремительно "дрыгать" ножкой, тем меняя результирующая площадь импульса за единицу времени.
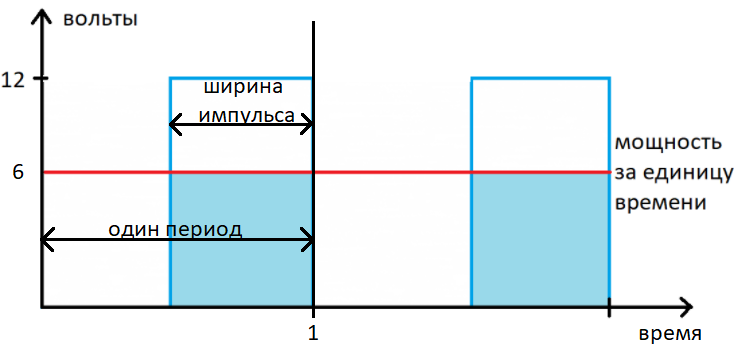
На этом принципе устроена широтно-импульсная модуляция, она же ШИМ. Меняя время (ширину) импульса за период мы изменяем выдаваемую мощность. На рисунке выше, показано два периода ШИМа. Каждый период имеет отношение площади импульса к площади всего периода 0.5, те половину времени периода контроллер выдает высочайший уровень сигнала, другую половину маленький. Отношение времени высокого уровня сигнала к времени низкого именуется скважностью. Красноватая линия на графике отражает результирующую мощность за единицу времени, по ней видно что при скважности 0.5 мощность также свалилась на одну вторую (с 12 до 6 Вт). Отменная новость заключается в том, что, ШИМ в контроллерах реализован аппаратно. Так что для регулирования чего-то довольно его запустить и, по необходимости, изменять скважность.
Для неизменного тока, режим ШИМа оптимален, при этом чем более инерционный устройство мы к нему подключаем, тем наименьшую частоту ШИМа можно применять. Для огромного ТЭНа довольно чуть не 1-го герца, а вот для светодиодов лучше применять частоту побольше. Кстати частота ШИМа в подсветке экрана ноутбука, часто оказывается чуть не решающим фактором при покупке, так как, при очень низкой частоте, глаза будут стремительно уставать.
Если испытать провернуть трюк с ШИМом для переменного напряжения, мы увидим что все сломалось и мощность закончила регулироваться линейно
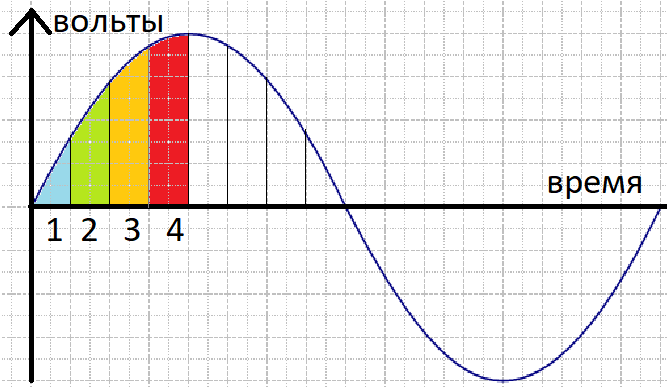
однообразные промежутки времени стали давать нам разную площадь, а означает разную мощность. Но, если разбить приобретенные отрезки на на ещё более маленькие, то процентное соотношение ширины импульса к ширине куска будет выравниваться.
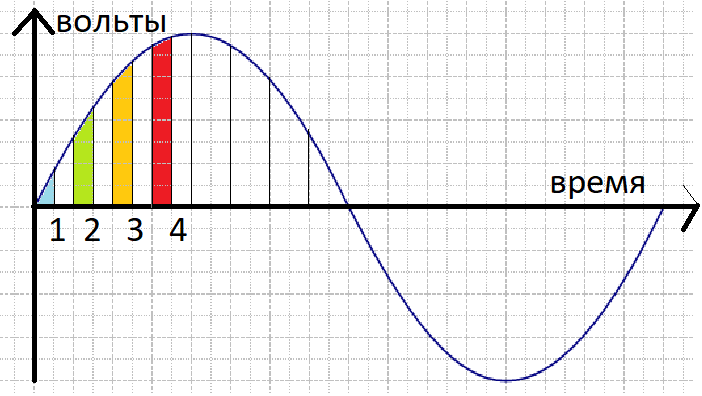
Если мы возьмем равный процент выдаваемой мощности от каждого куска, в итоге мы получим таковой же процент, от мощности всей волны, а на выходе мы получим линейный регулятор мощности для переменного тока. При этом чем огромную частоту будет иметь ШИМа, тем на большее количество кусочков он разобьет синусоиду, а означает мы получим огромную линейность.
Это было бы решением всех заморочек, но в моем случае устройством коммутировавшим нагрузку был не резвый транзистор, а симистор — неспешный устройство, с наивысшими рабочими частотами в границах нескольких сотен герц, к тому же симистор можно только открыть, закроется он сам при переходе через ноль. На таких частотах управлять переменным напряжением которое имеет частоту 50 Гц, линейно не получится. Потому тут необходимо применять некий другой подход и как раз для него, кроме симисторов, была установлена схема перехода через ноль.
В случае с симисторами лучше разбить синусоиду на кусочки с одинаковыми площадями и записать время каждого такового куска в таблицу. Тогда каждое последующее значение из таблицы будет линейно наращивать мощность.
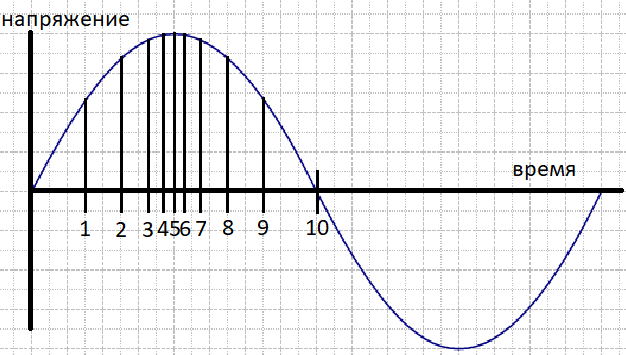
На графике выше полуволна синусоиды разбита на части различные по времени, но имеющие одинаковую площадь, а означает несущие внутри себя одинаковую мощность. Все что нам остается выполнить это загрузить таблицу с временными интервалам в наш котроллер, синхронизировать некий из его таймеров с частотой синусоиды, для этого применяется схема перехода через ноль, и просто брать из таблички необходимое значение, в течении которого будет высочайший уровень. Сущность способа похожа на ШИМ, но малость доработанный и синхронизированный с источником переменного напряжения.
Расчёт таблицы мощности
Сейчас можно перейти конкретно к расчёту.
Вначале задачка состоит в том дабы разбить синусоиду на необходимое нам количество кусочков, любой из которых будет иметь одинаковую площадь. На этом моменте, обычно проступает холодный пот, так-как площадь под графиком это и есть геометрическое определение интеграла. Соответственно нам необходимо будет взять интеграл от функции при всем этом найти такие пределы интегрирования, которые будут давать однообразный итог. Потом (будто бы расчёта интегралов не много!) приобретенные пределы необходимо будет перевести во время задержки (время в течении которого будет сохранятся высочайший уровень). После этого приобретенное время перевести в понятное для контроллера число — количество тиков таймера. Звучит жутко, а по факту на данный момент разберёмся:
Во первых сама функция — как было написано выше мощность это произведение тока на напряжение, для переменного тока (без сдвига фаз), это утверждение также правильно, но, так-как и ток и напряжение изменяются с течением времени P=IU преобразуется в P=I*sin(t) * U*sin(t). Так как амплитуда синусоиды нас сильно не тревожит, уравнение вырождается до P=sin^2(t).
Неопределённый интеграл от квадрата синуса
Сейчас необходимо подобрать пределы для определенных интегралов. Выберем, как частей мы желаем разбить нашу синусоиду: я избрал 100, дабы можно было регулировать мощность с шагом в 1%.
Итак мы отыскали чему будет равен неопределённый интеграл и даже избрали шаг. Сейчас необходимо подобрать пределы интегрирования. Смысл их подбора состоит в том, дабы значение определенного интеграла было неизменным при их смене. Напомню, что неопределенный интеграл это формула, а определённый полностью конкретное число. Определённый интеграл считается по формуле:
Другими словами мы берем неопределённый интеграл, подставляем в него верхнее число, потом нижнее, и вычитаем 2-ое из первого.
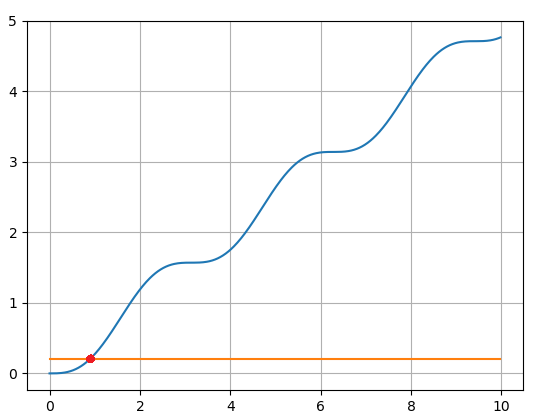
Наш неопределённый интеграл является смешанной тригонометрической функцией, а означает не имеет общего аналитического решения. В большинстве случаев такие функции решаются или числовыми, или графическими способами. Графический способа состоит в том что мы строим графики для правой и левой части уравнения их скрещение будет решением уравнения. На рисунке показано решение уравнения для 0.2
Вместе с графическим способом можно применять численный, другими словами подбор решения. Будем подставлять в неопределённый интеграл числа до того времени пока не найдём решение). Можно применять лист и бумажку дабы попрактиковаться в арифметике, можно онлайн калькулятор, я же буду применять Python и библиотеки numpy:
Отлично мы получили массив чисел (пределов интегрирования!), валидность этих чисел можно проверить подставив их в интеграл. В итоге должна получится площадь равная избранному шагу! Сейчас, если подставить приобретенные числа на график мощности, должна получится такая картина:
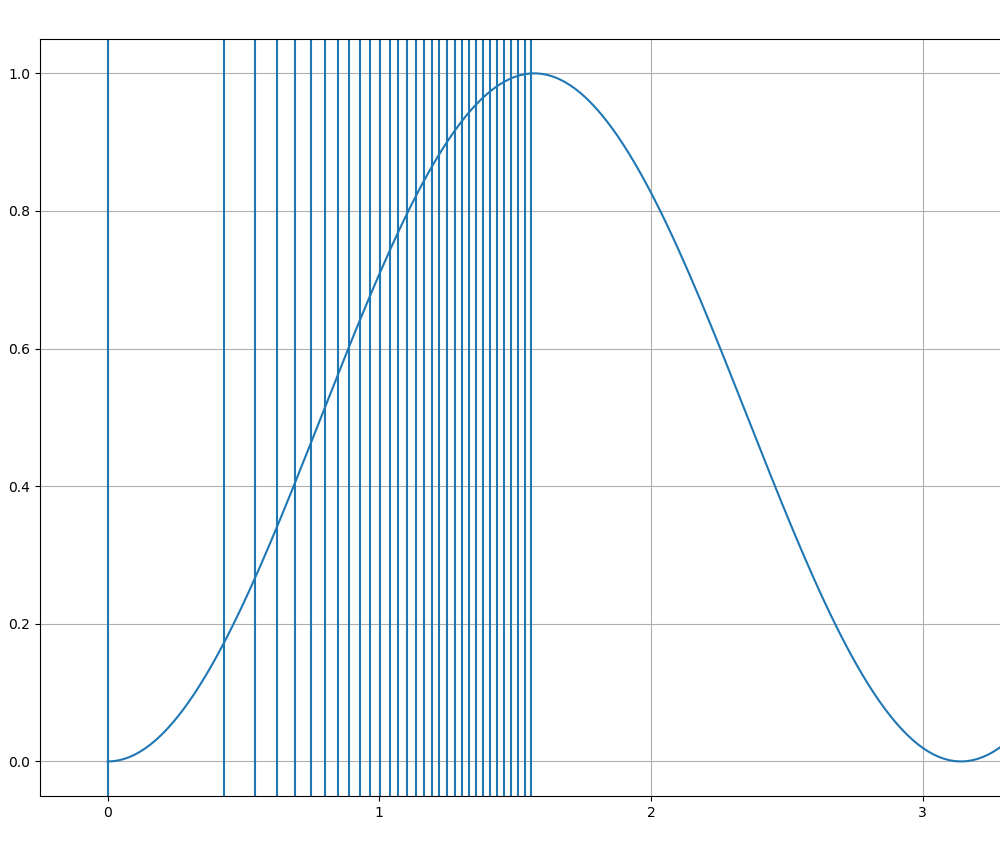
Если все сошлось, то можно двигаться далее и задать получившимся числам размерность времени, так как на данный момент они в радианах. Дабы это выполнить необходимо узнать угловую скорость, для частоты сети, другими словами количество радиан за секунду.
Тогда узнаем сколько сколько продолжается одна радиана
Сейчас, значения задержек в радианах, превратим во время, умножив каждое значение на период радианы (T). Проверим ход собственной мысли: действительно-ли получится время задержки, если помножить задержку, на период? Задержка имеет размерность радиан, период — секунд за радиану, мы желаем их перемножить. Тогда рад * ( сек / рад ) = сек. Мы получили время, а означает ход мыслей должен быть верным.
Для расчётов я снова предпочту python:
На этом моменте мы получили универсальную таблицу задержек, сейчас нужно преобразовать её специально под микроконтроллер.
Расчёт таймера МК и перевод таблицы
Время нужно перевести в понятную для МК величину — количество переполнений таймера. Но поначалу нужно обусловится с частотой таймера: чем выше частота, тем поточнее он будет отмерять время, но с другой стороны, тем меньше времени будет оставаться на выполнение остальной программы. Тут нужно отыскать золотую середину.
Для определения мало допустимой частоты таймера, нужно отыскать числа в массиве с малой разностью между ними. Разность тем меньше, чем поближе в максимуму синусоиды мы двигаемся. Тогда возьмем задержку при которой синусоида добивается единицы и число перед ним, после этого найдем их разность:
5 мс — 4.9363 мс = 0.0636 мс
Получившееся число является очень допустимым периодом между прерываниями таймера, тогда через него найдём мало допустимую частоту
1 / 0.0636 = 15 КГц
Означает для данной точности в 1% будет довольно таймера с частотой 15КГц. Частота МК составляет 16 МГц, означает между прерываниями будет 1000 тактов микропроцессора, этого довольно для выполнения остальной части программы, так что можно смело настраивать таймер на заданную частоту.
Для опции таймера на определенную частоту, не кратную тактирующей применяется режим таймера CTC — Clear Timer on Compare. В этом режиме таймер досчитывает до данного числа и сбрасывается, после этого операция повторяется. Число при котором будет происходить совпадение считается по формуле
Число = Тактовая частота МК / предделитель таймера / избранная частота
Частота выбрана, сейчас необходимо перевести таблицу в тики таймера. Делать я это буду снова на Python
В общем-то на этом весь расчёт окончен, остается только отзеркалить получившийся массив для 2-ой половины полуволны и загрузить в МК. Дальше по прерыванию от синхроимпульса, необходимо подать малый уровень, на ножку управления симистором, запустить таймер и считать его переполнения (совпадения, тк. у нас режим CTC). Как количество переполнений достигнет подходящего числа из таблички, подаем высочайший уровень на управляющую ножку. На этом линейный регулятор мощности переменного напряжения готов!
Заключение
Надеюсь статья была понятна и её было любопытно читать. В дополнение хотелось бы сказать, сигнал перехода через ноль не идёт совершенно впору, потому может потребоваться дополнительная корректировка, дабы это поправить.
Код расчетов на python
Также, если кому-то будет любопытно, могу поделится исходником готового регулятора для ардуино.
АКТИВНАЯ, РЕАКТИВНАЯ И ПОЛНАЯ МОЩНОСТИ ЦЕПИ
Умножив стороны треугольников напряжений (см. векторные диаграммы рис. 2.9, б, 2.10, б, 2.11, б) на ток I, получим треугольники мощностей.
Стороны треугольников мощностей соответственно означают:
— Р = UrI = I 2 r — активная мощность цепи, Вт, кВт (рис 2.9, г, 2.10, г, 2.11,г и ж);
— QL = ULI = I 2 xL — реактивная индуктивная мощность цепи, обусловленная энергией магнитного поля, вар, квар (рис. 2.9, г);
— QС = UСI = I 2 хС — реактивная емкостная мощность цепи, обусловленная энергией электрического поля, вар, квар (рис. 2.10, г);
— Q = QL — QС = I 2 x — реактивная мощность цепи, вар, квар (рис 2.11, г и ж), это та мощность, которой приемник обменивается с сетью;
— S = UI = I 2 z — полная мощность цепи. В • А, кВ • А (рис. 2.9, г, 2.10, г, 2.11, г и ж);
— cos φ = r/z = P/S — коэффициент мощности цепи (рис. 2.9, г, 2.10, г, 2.11, г и ж).
Из треугольников мощностей можно установить следующие связи между Р, Q, S и cos φ:
За единицу активной мощности принят ватт (Вт) либо киловатт (кВт), реактивной мощности — вольтампер реактивный (вар) либо киловольтампер реактивный (квар), полной мощности — вольтампер (ВА) либо киловольтампер (кВ • А).
Реактивные (индуктивная, емкостная) мощности, обусловленные соответственно энергией магнитного поля индуктивности и электрического поля емкости, не совершают никакой полезной paботы, но они оказывают существенное воздействие на режим работы электрической цепи. Циркулируя по проводам трансформаторов, генераторов, движков, линий передач, они нагревают их. Потому расчет проводов и других частей устройств переменного тока создают, исходя из полной мощности S, которая учитывает активную и реактивную мощности.
Рис. 2.13. Схема включения устройств для измерения активной, реактивной и полной мощностей цепи, также ее характеристик
Коэффициент мощности имеет огромное практическое значение: он указывает, какая часть полной мощности является активной мощностью. Полная мощность и коэффициент мощности вместе с другими параметрами являются расчетными величинами и в конечном счете определяют габаритные размеры трансформаторов, генераторов, движков и других электротехнических устройств.
Измерение активной, реактивной, полной мощностей и cos φ, также характеристик цепи, к примеру r и L, можно произвести при помощи ваттметра, амперметра и вольтметра, включенных в цепь по схеме, изображенной на рис. 2.13.
Ваттметр определяет активную мощность Р цепи. Полная мощность цепи равна произведению показаний вольтметра и амперметра.
Активное сопротивление находят из формулы:
Полное сопротивление цепи
Индуктивность L определяют из формулы
Пример 2.1. Приборы, включенные в цепь рис 2.13, демонстрируют Р = 500 Вт, I = 5 А, U= 400 В.
Найти активное сопротивление r и индуктивность цепи L, если частота сети f = 50Гц.
Решение. Активное сопротивление цепи
r = P/I 2 = 500/5 2 = 20 Ом.
Индуктивное сопротивление цепи
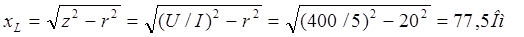
Пример 2.2. Найти ток, полную, активную и реактивную мощности, также напряжения на отдельных участках цепи, изображенной на рис. 2.11, а. если r = 40 Ом. L = 0,382 Гн, С = 35,5 мкФ, U = 220 В, частота сети f = 50 Гц.
Решение. Индуктивное сопротивление цепи
Емкостное сопротивление цепи
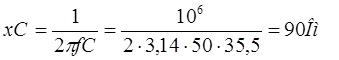
Полное сопротивление цепи
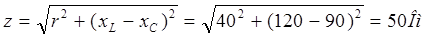
Ток в цепи:
I = U/z = 220/50 = 4,4 А.
Коэффициент мощности цепи:
Полная, активная и реактивная мощности:
S = UI = I 2 z = 220 • 4,4 = 4,42 • 50 = 970 В • А.
Р = S cos φ = I 2 r = 970 • 0,8 = 4,42 • 40 = 775 Вт;
Q = S sin φ = I 2 (xL — xС) = 970 • 0,56 = 4,42 (120 — 90) = 580 вар.
Напряжения на отдельных участках цепи:
Пример 2.3. Найти нрав нагрузки, полную, активную и реактивную мощности цепи, в какой секундные значения напряжения и тока составляют:
Решение. Угол исходной фазы напряжения (ψ1 = 60°) больше, чем тока (ψ2 = 30°), потому напряжение опережает по фазе ток на угол φ = ψ1 — ψ2 = 60 — 30 = 30° и нагрузка имеет активно-индуктивный нрав.
Полная мощность цепи:
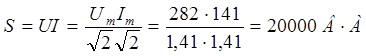
Активная мощность цепи:
Р = S cos φ = 20 000 cos 30° = 20 000 ( /2) — 17 300 Вт
Реактивная мощность цепи:
Q = S sin φ = 20 000 sin 30° = 20000 • 0,5 = 10 000 вар.
Мощность из тока и напряжения
Знать наибольший входной ток источника питания полезно при выборе требований к электросети, аварийного выключателя, кабеля питания переменного тока, разъемов и даже изолирующего трансформатора в плавучих блоках. Высчитать наивысшую силу входного тока достаточно легко, зная несколько главных характеристик и обычных математических действий.
Номинальная мощность источника питания высокого напряжения
Для всех источников питания компании Spellman указана номинальная наибольшая мощность в ваттах. Это 1-ый подходящий нам параметр; получить его можно из техпаспорта изделия. У большей части источников питания компании Spellman наибольшая номинальная мощность указана в номере модели. К примеру, SL30P300/115 — источник питания напряжением 30 кВ с положительной полярностью и наибольшей мощностью 300 Вт, работающий от входного напряжения переменного тока 115 В.
КПД источника питания
КПД источника питания — отношение мощности на входе к мощности на выходе. КПД обычно указывается в процентном виде либо в виде десятичной дроби меньше 1, к примеру, 80 % либо 0,8. Дабы выяснить входную мощность, поделим наивысшую выходную мощность на КПД:
300 Вт / 0,8 = 375 Вт
Коэффициент мощности
Коэффициент мощности — отношение реальной мощности к закрепляемой. Обычно он выражается в виде десятичной дроби меньше 1. Настоящая мощность указывается в ваттах, а закрепляемая — в вольт-амперах (ВА). У однофазовых импульсных источников питания без корректировки коэффициент мощности обычно достаточно низок, к примеру, 0,65. Импульсные источники питания без корректировки владеют более высочайшим коэффициентом мощности, к примеру, 0,85. Блоки питания с активной корректировкой коэффициента мощности могут владеть очень высочайшим коэффициентом мощности, например, 0,98. В приведенном выше примере применяется источник питания без корректировки с питанием от однофазовой полосы, таким макаром:
375 Вт / 0,65 = 577 ВА
Напряжение на входе
Нам следует знать входное напряжение переменного тока, для которого предназначен источник питания. В приведенном выше примере оно составляет 115 В. Это номинальное напряжение, в действительности оно указывается с допуском ±10 %. Дабы предугадать наихудший случай с низким напряжением в сети, отнимем 10 %:
115 В – 10 % = 103,5 В
Наибольшая сила переменного тока на входе
Взяв 577 ВА и разделив ее на 103,5 В, получаем:
577 ВА / 103,5 В = 5,57 А
Если напряжение на входе однофазовое, наш ответ — 5,57 А.
Трехфазное входное напряжение
Источники питания с трехфазным напряжением на входе владеют более высочайшим коэффициент мощности, чем однофазовые. Не считая того, из-за наличия 3-х фаз, питающих источник, фазовая сила тока будет наименьшей. Дабы выяснить силу тока одной фазы, поделим рассчитанную нами силу тока на входе на √3 (1,73).
Рассчитаем данные для следующего примера: STR10N6/208. Из технического паспорта STR узнаем, что наибольшая мощность — 6000 Вт, КПД 90 %, а коэффициент мощности 0,85. И хотя STR в силу собственной конструкции будет работать с напряжением до 180 В переменного тока, в данном примере его питание будет поступать от трехфазной сети 208 В. Наивысшую силу входного тока на одну фазу получаем следующим образом:
КПД источника питания:
6000 Вт / 0,9 = 6666 Вт
Коэффициент мощности:
6666 Вт / 0,85 = 7843 ВА
Напряжение на входе:
208 В – 10 % = 187 В
Наибольшая сила переменного тока на входе:
7843 ВА / 187 В = 41,94 А (если б сеть была однофазовой)
Пересчет для 3-х фаз на входе:
41,94 А / √3 (1,73) = 24,21 А на фазу
Таким макаром, у нас есть два уравнения, одно для однофазового и одно для трехфазного напряжения на входе:
Уравнение для наибольшей силы однофазового входного тока
Входной ток = наибольшая мощность/(КПД)(коэффициент мощности)(наибольшее входное напряжение)
Уравнение для наибольшей силы трехфазного входного тока
Входной ток = наибольшая мощность/(КПД)(коэффициент мощности)(наибольшее входное напряжение)(√3)
Данные расчеты входного тока предугадывают наихудший случай, исходя из того, что источник питания работает на наибольшей мощности с низким напряжением в полосы, также с учетом КПД и коэффициента мощности.