В этой статье мы разберем, что такое мощность трехфазного асинхронного мотора и как ее высчитать.
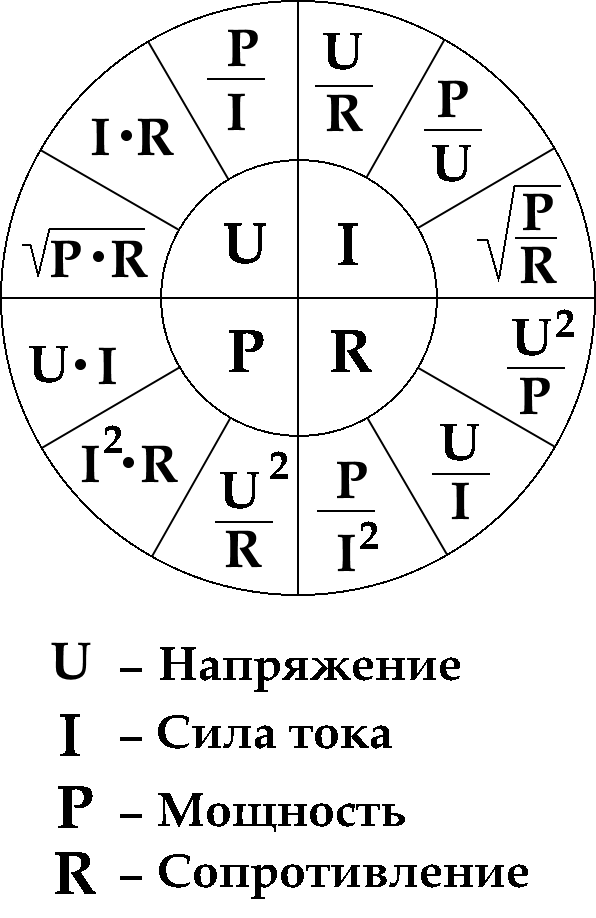
Понятие мощности электродвигателя
Мощность – пожалуй, важнейший параметр при выборе электродвигателя. Обычно она указывается в киловаттах (кВт), у привезенных из других стран моделей – в киловаттах и лошадиных силах (л.с., HP, Horse Power). Для справки: 1 л.с. примерно равна 0,75 кВт.
На шильдике мотора указана номинальная нужная (отдаваемая механическая) мощность. Это та мощность, которую мотор может отдавать механической нагрузке с заявленными параметрами без перегрева. В формулах номинальная механическая мощность обозначается через Р2.
Электрическая (потребляемая) мощность мотора Р1 всегда больше отдаваемой Р2, так как в любом устройстве преобразования энергии есть утраты. Главные утраты в электродвигателе – механические, обусловленные трением. Как понятно из курса физики, утраты в любом устройстве определяются через КПД (ƞ), который всегда наименее 100%. В этом случае справедлива формула:
КПД в движках находится в зависимости от номинальной мощности – у маломощных моделей он может быть наименее 0,75, у массивных превосходит 0,95. Приведенная формула справедлива для активной потребляемой мощности. Но, так как электродвигатель является активно-реактивной нагрузкой, для расчета полной потребляемой мощности S (с учетом реактивной составляющей) необходимо учесть реактивные утраты. Реактивная составляющая выражается через коэффициент мощности (cosϕ). С её учетом формула номинальной мощности мотора смотрится так:
Мощность и нагрев мотора
Номинальная мощность обычно указывается для температуры окружающей среды 40°С и ограничена предельной температурой нагрева. Так как самым слабеньким местом в движке исходя из убеждений перегрева является изоляция, мощность ограничивается классом изоляции обмотки статора. К примеру, для более распространенного класса изоляции F допустимый нагрев составляет 155°С при температуре окружающей среды 40°С.
В документации на электродвигатели приводятся данные, из которых видно, что номинальная мощность мотора падает при повышении температуры окружающей среды. С другой стороны, при должном охлаждении движки могут долгое время работать на мощности выше номинала.
Мы разглядели потребляемую и отдаваемую мощности, но следует сказать, что настоящая рабочая потребляемая мощность P (мощность на валу мотора на этот момент) всегда должна быть меньше номинальной:
Если нужно высчитать потребляемую активную мощность, используем следующую формулу:
Р1 = 1,73 · U · I · ƞ
Конкретно активную мощность определяют счетчики электроэнергии. В индустрии для измерения реактивной (и полной мощности S) используют дополнительное оборудование. При данном методе можно не применять приведенную формулу, а поступить проще – если мотор подключен в «звезду», измеренное значение тока умножаем на 2 и получаем ориентировочную мощность в кВт.
Расчет мощности с помощью счетчика электроэнергии
Этот метод прост и не просит дополнительных инструментов и познаний. Довольно подключить мотор через счетчик (трехфазный узел учета) и выяснить разницу показаний за строго определенный промежуток времени. К примеру, при работе мотора в течении часа разница показаний счетчика будет численно равна активной мощности мотора (Р1). Но дабы получить номинальную мощность Р2, необходимо пользоваться приведенной выше формулой.
Формула мощности тока
Электрический ток, на каком угодно участке цепи совершает некоторую работу (А). Допустим, что у нас есть случайный участок цепи (рис.1) между концами которого имеется напряжение U.
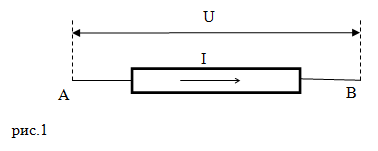
Работа, которая осуществляется при перемещении заряда равного 1 Кл между точками A и B (рис.1) будет равна U. В этом случае, если через проводник протекает ток силой I за время равное $\Delta t$ по обозначенному выше участку пройдет заряд (q) равный:
Поэтому, работа, которую совершает электрический ток на данном участке, равна:
$$A=U \cdot I \cdot \Delta t(2)$$
Нужно отметить, что выражение (2) является справедливым при I=const для любого участка цепи (в таком участке могут содержаться проводники 1–го и 2–го рода).
Определение и формула мощности тока
Мощность тока – есть работа тока в единицу времени:
Формулой для вычисления мощности можно считать выражение:
В этом случае, если участок цепи содержит источник тока, то формулу мощности можно представить в виде:
$$P=\left(\varphi_-\varphi_\right) I+\varepsilon I$$
где $\left(\varphi_-\varphi_\right)$ – разность потенциалов, $\varepsilon$ – ЭДС источника, который включен в цепь.
Выражение (5) является интегральной записью. Это выражение можно представить в дифференциальной форме, если применять понятие удельной мощности ($P_=\frac$ – мощность, развиваемая током в единице объема проводника):
где j – плотность тока, $\rho$ – удельное сопротивление.
Единицы измерения мощности тока
Основной единицей измерения мощности тока (как и мощности вообщем) в системе СИ является: [P]=Вт=Дж/с.
Выражение (4) используют в системе СИ для того, дабы дать определение единицы напряжения. Так, единицей напряжения (U) является вольт (В), который равен: 1 В= (1 Вт)/(1 А).
Вольтом именуют электрическое напряжение, которое порождает в электроцепи неизменный ток силы 1 А при мощности 1 Вт.
Примеры решения задач
Задание. Какой должна быть сила тока, которая течет через обмотку электрического мотора для того, дабы нужная мощность мотора (PA) стала наибольшей?Какова наибольшая нужная мощность? Если мотор неизменного тока подключен к напряжению U, сопротивление обмотки якоря – R.
Решение. Мощность, которую потребляет электроприёмник, идет на нагревание (PQ) и совершение работы (PA):
Мощность, идущую на нагревание можно высчитать как:
Потребляемую мощность найдем как:
Выразим $P_A$ из (1.1) и используем (1.2) и (1.3):
Для нахождения экстремума функции, которая представлена в выражении (1.4) найдем производную $\frac$ и приравняем ее к нулю:
Найдем наивысшую полезную мощность,используя выражение (1.4) и Imax:

испытанных создателя готовы посодействовать в написании работы хоть какой трудности
Мы посодействовали уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Выясни цена собственной работы за 15 минут!
Задание. Электрические лампочкис мощностями P1 и P2 номинальным напряжением U1=U2 соединяют последовательно (рис.2) и включают в сеть с неизменным напряжением U. Какова мощность, потребляемая первой лампочкой P1 * ).
Решение. Лампочки по условию задачи соединены последовательно, означает сила тока, текущая через лампочки одинакова, а падение напряжения на каждой из лампочек находится в зависимости от их сопротивлений. Разыскиваемую мощность можно отыскать как:
Сопротивления лампочек можно отыскать из данных в критериях номинальных мощностей:
Силу тока можно отыскать по закону Ома, беря во внимание, что лампочки соединены последовательно:
Виды мощности — определение и свойства
Одной из важнейших физических величин является мощность. Она связана с работой. В качестве примера можно привести человека, который подымается по ступенькам. Лестницу можно преодолеть шагами либо бегом. В этих ситуациях будет проделана однообразная работа, но в этом случае, когда человек бежит, работа осуществляется резвее.
В итоге мощность может выражаться скоростью либо интенсивностью выполнения работы. При увеличении мощности миниатюризируется время, нужное для совершения работы. Таким макаром, короткая формулировка мощности звучит, как скорость выполнения работы.
Мощность — является скалярной физической величиной, которая охарактеризовывает секундную скорость передачи количества энергии от одной физической системы к другой в процессе ее применения, и в общем случае определяется, как соотношение переданной энергии к времени передачи.
В системе СИ единицей измерения мощности является ватт, который соответствует энергии в 1 джоуль, переданной в течение 1 секунды ( 1 В т ≡ 1 Д ж / с ) . Какое-либо числовое значение мощности, указываемое в информационных источниках, в распространенных случаях предполагает конкретно таковой секундный временной интервал.
Согласно действующим интернациональным эталонам серии I S O / I E C 80000 , величину мощности обозначают эмблемой P строчный буковкой при записи формул механики и электродинамики. Этимология обозначения — или от лат. potestas, или от англ. power.
В русских литературных источниках и записях законов по физике можно повстречать обозначение мощности буковкой N. Отсутствуют четкие данные об этимологии данного обозначения.
Виды мощности, определение и свойства
По Интернациональной системе единиц (СИ) мощность можно измерить в ватт (Вт). Ватт равен одному джоулю за секунду (Дж/с). В теоретической физике и астрофизике мощность в распространенных случаях обозначают через эрг за секунду (эрг/с). Данная единица измерения является внесистемной. Мощность автомобилей, движков локомотивов и судов определяют в лошадиных силах, что не рекомендовано Интернациональной организации законодательной метрологии (МОЗМ).
Механическая мощность
В этом случае, когда тело движется под воздействием силы, данная сила совершает работу.
Мощность вычисляют, как скалярное произведение вектора силы на вектор скорости перемещающегося тела:
N = F · v = F · v · cos α ,
где F — определяет вектор силы;
v — является вектором скорости;
α — составляет угол между вектором скорости и силы;
F — модуль вектора силы;
v — модуль вектора скорости.
В этом случае, когда тело совершает вращательное движение, применима такая формула для определения мощности:
N = M · ω = 2 π · M · n 60 ,
где M — определяет момент силы;
ω — является обозначением угловой скорости;
n — частота вращения (число об/мин, об/мин).
Электрическая мощность
Электрическая мощность является физической величиной, чертой скорости, с которой передается либо преобразуется электроэнергия.
Моментальная электрическая мощность P ( t ) участка электрической цепи определяется таким макаром:
P ( t ) = I ( t ) · U ( t )
где I ( t ) — является моментальным током через участок цепи;
U ( t ) — определяет секундное напряжение на данном участке.
В процессе исследования сетей переменного тока оперируют не только лишь общефизическим понятием моментальной мощности, но и применяют следующие определения:
- активная мощность, соответствует средней величине моментальной мощности в течение периода времени;
- реактивная мощность, соответственная энергии, которая циркулирует без диссипации от источника к потребителю и в оборотном направлении;
- полная мощность, определяемая через произведение имеющихся значений электрического тока и напряжения без учета сдвига фаз.
Секундную активную мощность определяют таким макаром:
p ( t ) = 1 2 · U m · I m · cos φ — 1 2 · U m · I m · cos φ cos ( 2 ω t ) .
Уравнение моментальной реактивной мощности при φ > 0 :
q ( t ) = 1 2 · U m · I m · sin φ · cos \ Bigl ( 2 ω t + π 2 \ Bigr ) ,
q ( t ) = 1 2 · U m · I m · sin φ · cos \ Bigl ( 2 ω t — π 2 \ Bigr ) .
Моментальная полная мощность:
s ( t ) = 1 2 · U m · I m · cos φ — 1 2 · U m · I m · c o s \ Bigl ( 2 ω t — φ \ Bigr ) ,
где I m — определяет амплитуду тока;
U m — является амплитудой напряжения;
φ — угол между исходным углом напряжения ψ u и исходным углом силы тока ψ i — ( φ = ψ u — ψ i ) ;
ω — угловая скорость;
Гидравлическая мощность
Гидравлическая мощность гидромашины либо гидроцилиндра равна произведению перепада давления на машине (разности давлений на входе и выходе) на расход воды:
где Q H — расход воды, м 3 / с ;
P H — перепад давления, Па.
В качестве примера можно разглядеть насосную установку НП-89Д, которой оснащают Су-24, Ту-134 и Ту-154. Производительность данной модели насоса составляет 55 л/мин (около 0 , 000917 м 3 / с ) при давлении 210 кгс/см2 (21 МПа). Таким макаром, гидравлическая мощность насоса равна примерно 19,25 кВт.
Приборы для измерения мощности
Ваттметры (включая варметры) — являются измерительными устройствами, при помощи которых определяют мощность электрического тока либо электрического излучения.
Зависимо от мотивированного предназначения и спектра частот ваттметры систематизируют на некоторое количество видов:
- низкочастотные (и неизменного тока);
- радиочастотные;
- оптические.
Ваттметры радиодиапазона, исходя из предназначения, бывают 2-ух типов:
- проходящей мощности, которые включают в разрыв полосы передачи;
- поглощаемой мощности, созданные для подключения к концу полосы и играющие роль согласованной нагрузки.
Согласно способу многофункционального преобразования измерительной инфы и ее отображения для оператора, ваттметры подразделяют на следующие группы:
- аналоговые (показывающие и самопишущие);
- цифровые.
Как отыскать мощность, формулы и примеры задач
Основная формула для расчета мощности имеет вид:
где, P — мощность, E — энергия, t — время.
Средняя величина мощности за промежуток времени Δ t :
Интеграл по времени от моментальной мощности за промежуток времени вычисляют, как полную переданную энергию за этот период времени:
∫ t 0 t 1 P d t = E .
Мотор подъемной техники обладает мощностью 3,5 л. с. Нужно найти массу груза, который такая машина может поднять на высоту 15 м за 2 мин. (1 л.с.=736 Вт).
Мощность мотора составляет 3 , 5 · 736 = 2576 В т .
m = P t g h = 2576 · 2 · 60 10 · 15 = 2060 , 8
Нужна найти время, которое нужно затратить на откачку 10 т воды из шахты при помощи насоса мощностью 1,5 кВт. Высота подъема составляет 20 м.
В связи с тем, что планируется откачать всю воду, работу можно выразить при помощи следующего уравнения:
Согласно формуле мощности:
t = A P = m g h P = 10000 · 10 · 20 1500 = 1333 , 3
После перевода времени в минутки, получим 22,3 мин.
Ответ: 22,3 минутки
При помощи насоса было поднято 7 , 2 м 3 воды за 8 мин на высоту 10 м. Нужна найти, какой мощностью обладает насос.
Масса воды в данном объеме равна:
P = A t = m g h t = ρ V g h t = 1000 · 7 , 2 · 10 · 10 8 · 60 = 1500
Трактор вспахал 300 м полей за 1,5 мин, развивая при всем этом мощность 25,8 кВт. Нужна найти силу сопротивления, которую преодолевает трактор в процессе работы.
Согласно определению мощности:
F = P t S = 25800 · 90 300 = 7740
Ответ: 7 , 74 к Н .
Поезд, масса которого составляет 6 · 10 5 к г , совершает равномерное движение со скоростью 36 к м / ч . Нужна высчитать, какую мощность развивает тепловоз, преодолевая силу трения в 0,002 веса поезда.
Прежде всего следует перевести скорость в м/c:
υ = 36000 3600 = 10
Мощность можно найти таким макаром:
P = υ F = υ F t r = υ k m g = 10 · 0 , 002 · 6 · 10 6 = 120000
Игрушечная машинка, поднимаясь на горку с неизменным уклоном, способна развивать наивысшую скорость υ 1 = 5 к м / ч . Когда машинка спускается с этой же горки, она разгоняется до υ 2 = 10 к м / ч . Считая силу сопротивления пропорциональной скорости игрушки, необходимо найти наивысшую скорость, с которой машинка способна ехать в горку, если мощность мотора вырастет в n = 2 раза. Ответ выразить в км/ч, округлив до 10-х. Трение в осях отсутствует.
Зависимость силы сопротивления от скорости можно записать в виде уравнения:
Машинка совершает работу, преодолевая силы сопротивления, так как перемещается и забирается на горку. В общем виде совершаемую работу при движении в гору можно записать таким макаром:
A 1 = F S + m g h = F υ 1 t + m g S sin α = k υ 1 2 t + m g υ 1 t sin α = C υ 1 2 + D υ 1
где C и D — коэффициенты, которые учитывают все характеристики, кроме скорости.
В таком случае, мощность равна:
N = A 1 t = C ‘ υ 1 2 + D ‘ υ 1
Дальше можно разглядеть ситуацию, когда машинка спускается с горки. Некоторую часть работы (по подъему) сейчас делает сама сила тяжести, сняв эту нагрузку с мотора, потому:
A 2 = F S — m g h = F υ 2 t — m g S sin α = k υ 2 2 t — m g υ 2 t sin α = C υ 2 2 — D υ 2
Мощность в таком случае составит:
N = A 2 t = C ‘ υ 2 2 — D ‘ υ 2
Сравнив записанные выражения, получим:
C ‘ υ 2 + D ‘ υ = C ‘ υ 2 2 — D ‘ υ 2
C ‘ D ‘ = 1 υ 2 — υ 1 = 1 5
Потом следует разглядеть движение машинки в горку с двойной мощностью мотора:
2 N = A 3 t = C ‘ υ 3 2 + D ‘ υ 3
Приравняв мощности, получим:
2 C ‘ υ 1 2 + 2 D ‘ υ 1 = C ‘ υ 3 2 + D ‘ υ 3
2 C ‘ υ 1 2 + 10 C ‘ υ 1 = C ‘ υ 3 2 + 5 C ‘ υ 3
2 υ 1 2 + 10 υ 1 = υ 3 2 + 5 υ 3
υ 3 2 + 5 υ 3 — 100 = 0
D = 25 + 400 = 425
υ 3 = — 5 ± 425 2 = 7 , 8
Ответ: 7 , 8 к м / ч
Машина, поднимаясь на гору с неизменным уклоном, способна развивать наивысшую скорость υ 1 = 100 к м / ч . Во время движении вниз с этой же горы она разгоняется до υ 2 = 200 к м / ч . Считая силу сопротивления пропорциональной квадрату скорости автомобиля, нужна найти наивысшую скорость, которую может развивать машина, перемещаясь по горизонтальному участку дороги. Ответ нужна выразить в км/ч, округлив до целых. Трение в какой-нибудь степени в осях отсутствует. Мощность машины можно считать неизменной величиной.
Сила сопротивления находится в зависимости от скорости:
Машина совершает работу, преодолевая силу сопротивления, так как движется и забирается в гору. Общую совершаемую работу при движении в гору можно выразить при помощи уравнения:
A 1 = F S + m g h = F υ 1 t + m g S sin α = k υ 1 3 t + m g υ 1 t sin α = C υ 1 3 + D υ 1
где C и D — коэффициенты, учитывающие все свойства, кроме скорости.
Мощность определяется таким макаром:
N = A 1 t = C ‘ υ 1 3 + D ‘ υ 1
Дальше можно разглядеть ситуацию, когда машина спускается с горы. Определенную часть работы (по подъему) в данном случае делает сама сила тяжести, сняв эту нагрузку с мотора, потому:
A 2 = F S — m g h = F υ 2 t — m g S sin α = k υ 2 3 t — m g υ 2 t sin α = C υ 2 3 — D υ 2
N = A 2 t = C ‘ υ 2 3 — D ‘ υ 2
Приравняв правые части уравнений для мощности, коэффициенты будут соотнесены следующим образом:
C ‘ υ 3 + D ‘ υ = C ‘ υ 2 3 — D ‘ υ 2
C ‘ D ‘ = υ 2 + υ 1 υ 2 3 — υ 1 3 = 300 7 · 10 6 = 3 7 · 10 — 4
Мощность при рассмотрении движения по ровненькому участку пути составит:
N = A 3 t = C ‘ υ 3 3
После приравнивая значений мощности, получим:
C ‘ υ 1 3 + D ‘ υ 1 = C ‘ υ 3 3
υ 1 3 + 7 3 · 10 4 υ 1 = υ 3 3
υ 3 = υ 1 3 + 7 3 · 10 4 υ 1 3 = 100 3 + 7 3 · 10 4 · 100 3 = 100 10 3 3 = 149