С стародавних времен людей волнует идея о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. По сути это два очень сильно связанных между собой понятия. То, как стремительно можно добраться из 1-го пт в другой на летательном аппарате в наше время, зависит стопроцентно от скорости. Разглядим же методы и формулы расчета этого показателя, также времени и расстояния.
Как высчитать скорость?
По сути, высчитать ее можно несколькими методами:
- через формулу нахождения мощности;
- через дифференциальные исчисления;
- по угловым характеристикам и т.д..
В этой статье рассматривается самый обычной метод с самой обычный формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также находятся эти характеристики. Формула смотрится следующим образом:
- v — скорость объекта,
- S — расстояние, которое пройдено либо должно быть пройдено объектом,
- t — время, за которое пройдено либо должно быть пройдено расстояние.
Видите ли, в формуле первого класса средней школы нет ничего сложного. Подставив надлежащие значения заместо буквенных обозначений, можно высчитать быстроту передвижения объекта. К примеру, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Поначалу нужна перевести 1 час 30 минут в часы, так как почти всегда единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, так как 30 минут есть половина либо 1/2 либо 0,5 часа. Сложив совместно 1 час и 0,5 часа получим 1,5 часа.
Сейчас необходимо подставить имеющиеся значения заместо буквенных знаков:
v=100 км/1,5 ч=66,66 км/ч
Тут v=66,66 км/ч, и это значение очень ориентировочное (незнающим людям об этом лучше прочесть в специальной литературе), S=100 км, t=1,5 ч.
Таким нехитрым методом можно отыскать скорость через время и расстояние.
А что делать, если необходимо отыскать среднее значение? В принципе, вычисления, показанные выше, и дают в конечном итоге итог среднего значение искомого нами параметра. Но можно вывести и поболее четкое значение, если понятно, что на некоторых участках по сопоставлению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
vср=(v1+v2+v3+. +vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.
Эту же формулу можно записать по другому, используя путь и время, за которое объект прошел этот путь:
- vср=(S1+S2+. +Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
- S1, S2, Sn — отдельные неравномерные участки всего пути,
- t — общее время, за которое объект прошел все участки.
Можно записать применять и таковой вид вычислений:
- vср=S/(t1+t2+. +tn), где S — общее пройденное расстояние,
- t1, t2, tn — время прохождения отдельных участков расстояния S.
Но можно записать эту же формулу и в более четком варианте:
vср=S1/t1+S2/t2+. +Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.
Таким макаром, совсем не сложно отыскать разыскиваемый параметр, используя данные выше формулы. Они очень ординарны, и как уже было обозначено, применяются в исходных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более непростой вид, больше переменных и различных коэффициентов. Это необходимо для получения более четкого значения характеристик.
Другие методы вычисления
Существую и другие методы и способы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:
N=F*v*cos α , где N — механическая мощность,
cos α — косинус угла между векторами силы и скорости.

Методы вычисления расстояния и времени
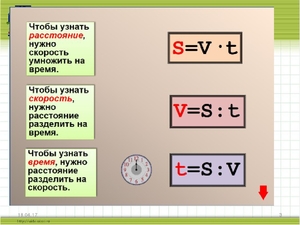
Можно и напротив, зная скорость, отыскать значение расстояния либо времени. К примеру:
S=v*t, где v — понятно что такое,
S — расстояние, которое нужна отыскать,
t — время, за которое объект прошел это расстояние.
Таким макаром рассчитывается значение расстояния.
Либо вычисляем значение времени, за которое пройдено расстояние:
t=S/v, где v — все та же скорость,
S — расстояние, пройденный путь,
t — время, значение которого в этом случае необходимо отыскать.
Для нахождения средних значений этих характеристик существует достаточно много представлений как данной формулы, так и всех других. Главное, знать главные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше назубок. Если же уяснить не выходит, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью отыскать время, расстояние и другие характеристики, используя нужные, правильные методы их вычисления.
И это еще не предел!
Видео
В нашем видео вы отыщите достойные внимания примеры решения задач на нахождение скорости, времени и расстояния.
Поставь лайк, это принципиально для наших создателей, подпишись на наш канал в Yandex.Дзен и вступай в группу Вконтакте
Работа, мощность, КПД
Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела сначала процесса и в его конце. А мощность – это работа за секунду. Коэффициент полезного деяния (КПД) – это дробное число. Наибольший КПД равен единице, но, нередко, КПД меньше единицы.
Работы силы, формула
Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).
Рис. 1. Сила перемещает тело и совершает работу
Работа силы — это скалярное произведение вектора силы на вектор перемещения.
Работу, совершаемую силой, можно посчитать, используя векторный либо скалярный вид записи таковой формулы:
Векторный вид записи
Для решения задач правую часть этой формулы комфортно записывать в скалярном виде:
\[ \large \boxed < A = \left| \vec\right| \cdot \left| \vec \right| \cdot cos(\alpha) >\]
\( F \left( H \right) \) – сила, перемещающая тело;
\( S \left( \text \right) \) – перемещение тела под действием силы;
\( \alpha \) – угол между вектором силы и вектором перемещения тела;
Работу обозначают эмблемой \(A\) и определяют в Джоулях. Работа – это скалярная величина.
В случае, когда сила неизменная, формула позволяет высчитать работу, совершенную силой за полное время ее деяния.
Если сила меняется с течением времени, то в каждый определенный момент времени будем получать секундную работу. Эти, секундные значения для различных моментов времени будут различаться.
Разглядим несколько случаев, следующих из формулы:
- Когда угол между силой и перемещением острый, работа силы положительная;
- А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
- Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
Работа — разность кинетической энергии
Работу можно высчитать еще одним методом — измеряя кинетическую энергию тела сначала и в конце процесса движения. Разглядим таковой пример. Пусть автомобиль, движется по горизонтальной прямой и, при всем этом наращивает свою скорость (рис. 2). Масса автомобиля 1000 кг. Сначала его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам за секунду. Найдем работу, которую пришлось сделать, дабы ускорить этот автомобиль.
Рис. 2. Автомобиль движется прямолинейно и наращивает свою скорость
Для этого посчитаем энергию движения автомобиля сначала и в конце разгона.
\( E_ \left(\text \right) \) – исходная кинетическая энергия машины;
\( E_ \left(\text \right) \) – конечная кинетическая энергия машины;
\( m \left( \text\right) \) – масса автомобиля;
\( \displaystyle v \left( \frac>\right) \) – скорость, с которой машина движется.
Кинетическую энергию будем вычислять, используя формулу:
\[ \large E_ = 1000 \cdot \frac> = 500 \left(\text \right) \]
\[ \large E_ = 1000 \cdot \frac> = 50000 \left(\text \right) \]
Сейчас найдем разницу кинетической энергии в конце и сначала разгона.
\[ \large \Delta E_ = 50000 – 500 = 49500 \left(\text \right) \]
Означает, работа, которую потребовалось совершить, дабы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, приравнивается 49500 Джоулям.
Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно отыскивать разность кинетической энергии, а можно — разность энергии возможной.
Работа силы тяжести — разность возможной энергии
Разглядим сейчас следующий пример. Яблоко массой 0,2 кг свалилось на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница размещается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.
Рис. 3. На рисунке обозначено изначальное 1 положение тела (яблока) и его конечное 2 положение, отмечены высоты для подсчета работы по вертикальному перемещению тела
Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.
\( E_ \left(\text \right) \) – исходная возможная энергия яблока;
\( E_ \left(\text \right) \) – конечная возможная энергия яблока;
Примечание: Работу можно высчитать через разность возможной энергии тела.
Потенциальную энергию будем вычислять, используя формулу:
\[ \large E_
= m \cdot g \cdot h\]
\( m \left( \text\right) \) – масса яблока;
\( h \left( \text\right) \) – высота, на которой находится яблоко относительно поверхности земли.
Исходная высота яблока над поверхностью земли равна 3 метрам
\[ \large E_ = 0,2 \cdot 10 \cdot 3 = 6 \left(\text \right) \]
Возможная энергия яблока на столе
\[ \large E_ = 0,2 \cdot 10 \cdot 1 = 2 \left(\text \right) \]
Сейчас найдем разницу возможной энергии яблока в конце падения и перед его началом.
\[ \large \Delta E_
= 2 – 6 = — 4 \left(\text \right) \]
Принципиально держать в голове: Когда тело падает на землю, его возможная энергия миниатюризируется. Сила тяжести при всем этом совершает положительную работу!
Дабы работа вышла положительной, в правой части формулы перед \( \Delta E_
\) дополнительно допишем символ «минус».
Означает, работа, которую потребовалось совершить силе тяжести, дабы яблоко массой 0,2 кг свалилось с высоты 3 м на высоту 1 метр, приравнивается 4 Джоулям.
Примечания:
- Если тело падает на землю, работа силы тяжести положительна;
- Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при всем этом положительна, а работа силы тяжести будет отрицательной;
- Сила тяжести относится к ограниченным силам. Для ограниченных сил перед разностью возможной энергии мы дописываем символ «минус»;
- Работа силы тяжести не находится в зависимости от линии движения, по которой двигалось тело;
- Работа для силы \(\displaystyle F_>\) зависит только от разности высот, в каких тело находилось в конечный и исходный моменты времени.
Набросок 4 иллюстрирует факт, что для силы \(\displaystyle F_>\) работа зависит только от разности высот и не находится в зависимости от линии движения, по которой тело двигалось.
Рис. 4. Разность высот между исходным и конечным положением тела во всех случаях на рисунке одинакова, потому, работа силы тяжести для представленных случаев будет одинаковой
Мощность
В механике мощность нередко обозначают знаками N либо P и определяют в Ваттах в честь шотландского изобретателя Джеймса Уатта.
Примечание: Знак \(\vec\) применяется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Дабы не появилось неурядицы, мощность заместо N будем обозначать эмблемой P. Знак P – 1-ая буковка в британском слове power – мощность.
Мощность – это работа, совершенная за секунду (энергия, затраченная за 1 сек).
Расчет работы осуществляем, используя всякую из формул:
\[ \large A = \Delta E_ \]
\[ \large A = \Delta E_
\]
\[ \large A = F \cdot S \cdot cos(\alpha) \]
Разделив эту работу на время, в течение которого она совершалась, получим мощность.
Если работа совершалась равными частями за однообразные интервалы времени – мощность будет неизменной величиной.
Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.
Еще одна формула для расчета мощности
Еще есть один метод расчета мощности, когда сила перемещает тело и при всем этом скорость тела не изменяется:
\[ \large P = \left( \vec , \vec \right) \]
Формулу можно записать в скалярном виде:
\[ \large P = \left| \vec \right| \cdot \left| \vec \right| \cdot cos(\alpha) \]
\( F \left( H \right) \) – сила, перемещающая тело;
\( \displaystyle v \left( \frac> \right) \) – скорость тела;
\( \alpha \) – угол между вектором силы и вектором скорости тела;
Когда векторы \(\vec\) и \(\vec\) параллельны, запись формулы упрощается:
Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если поточнее, обнаружив производную обеих частей уравнения).
КПД – коэффициент полезного деяния. Обычно обозначают греческим эмблемой \(\eta\) «эта». Единиц измерения не имеет, выражается или десятичной дробью, или в процентах.
Примечания:
- Процент – это дробь, у которой в знаменателе число 100.
- КПД — это или верная дробь, либо дробь, равная единице.
Вычисляют коэффициент \(\eta\) для какого-нибудь устройства, механизма либо процесса.
\( \large A_> \left(\text \right)\) – нужная работа;
\(\large A_> \left(\text \right)\) – вся затраченная для выполнения работы энергия;
Примечание: КПД нередко меньше единицы, так как обычно есть энергопотери. Коэффициент полезного деяния не может быть больше единицы, так как это противоречит закону сохранения энергии.
Величина \(\eta\) является дробной величиной. Если числитель и знаменатель дроби поделить на одно и то же число, приобретенная дробь будет равна начальной. Используя данный факт, можно вычислять КПД, используя мощности:
Как высчитать скорость по силе и массе: несколько подходов и примеры заморочек
В статье дискуссируются несколько подходов к вычислению скорости по силе и массе, также решенные препядствия.
Дабы вычислить скорость, мы должны осознать, как далековато уходит масса объекта при приложении силы. Скорость объекта — это не что другое, как величина его вектора скорости. Вот почему мы можем высчитать скорость по силе и массе, используя законы Ньютона, кинематическое уравнение движения и формулы работы-энергии.

Как высчитать скорость
от силы и массы
Как высчитать скорость по силе и массе, используя 2-ой закон Ньютона?
Давайте вычислим скорость по силе и массе, используя 2-ой закон движения Ньютона.
2-ой закон Ньютона связывает скорость конфигурации скорости либо ускорения с приложенной силой и массой. Дабы вычислить скорость по второму закону Ньютона, нам поначалу необходимо осознать разницу между скоростью и скоростью, а потом вычислить значение скорости, исходя из скорости конфигурации скорости.
Согласно 2-ой закон Ньютона,
В то время как v0 — исходная скорость, v — конечная скорость.
До того как рассчитывать скорость по закону Ньютона, давайте разберемся в разнице между скоростью и скоростью.
Разница между скоростью и скоростью
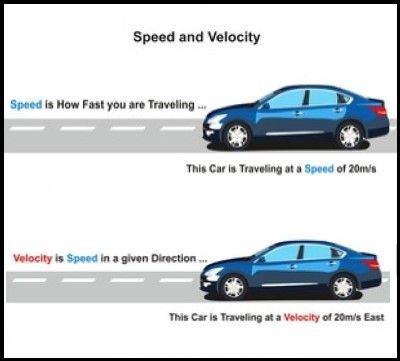
Скорость против скорости
(Кредит: Shutterstock)
Когда автомобиль проехал определенное расстояние d за время t, мы называем его скорость v.
Как вы понимаете, время от времени нам необходимо поменять направление во время движения из-за пробок либо по другим причинам; в данном случае мы измеряем смещение заместо расстояния d в интервале времени t.
Уравнение (*) преобразуется в скорость v как,
Смещение — это кратчайшее расстояние между конечным и исходным расстоянием, но его величина меньше либо равна общему расстоянию d.

Расстояние против смещения
(Кредит: Shutterstock)
Так как скорость не равна нулю либо никогда не миниатюризируется с течением времени, величина скорости становится значением скорости, когда время приближается к нулю.
Это значит скорость v гласит нам, как стремительно машина. В то время как скорость v гласит нам как о скорости автомобиля, так и о его направлении. Потому мы окрестили скорость величиной вектора скорости .
Автомобиль массой 1000 кг в состоянии покоя проехал около 1 часа при силе 6 х 10 4 Применяется N. Высчитайте скорость автомобиля.
Данный:
Формула:
Решение:
Скорость автомобиля рассчитывается с внедрением 2-ой закон движения Ньютона.
Так как автомобиль вначале находится в состоянии покоя, v0 = 0 и t0 = 0
Подставляя все значения,
Преобразуем скорость в скорость в метрах за секунду.
1 час = 3600 секунд
Автомобиль движется со скоростью 16.6 м / сек.
Как высчитать скорость по силе и массе, используя кинематическое уравнение движения?
Давайте вычислим скорость по силе и массе, используя 2-ое кинематическое уравнение движения.
2-ое кинематическое уравнение движения связывает общее пройденное расстояние объекта с исходной скоростью и ускорением. Когда мы ввели формулу ускорения из второго закона Ньютона в кинематическое уравнение, мы получили формулу, которая рассчитывала скорость на базе приложенной силы и ее массы.
2-ое кинематическое уравнение движения:

Как высчитать скорость по силе и массе при помощи кинематического уравнения
Парашютист массой 60 кг выпрыгивает из самолета и за 1 минутку добивается земли. Если сила, воздействующая на парашютиста по воздуху, составляет 800 Н, какова скорость парашютиста?
Данный:
t = 1 минутка = 60 секунд
Отыскать: v =?
Формула:
Решения:
Скорость парашютиста рассчитывается при помощи 2-ое кинематическое уравнение движения.
Так как парашютист вначале находится в состоянии покоя относительно плоскости, поэтому, d0 = 0 и v0 = 0.
С скорость v= d / t
Подставляем все значения
Скорость парашютиста 400 м / сек.
Как высчитать скорость по силе и массе, используя формулу работы-энергии?
Давайте вычислим скорость по силе и массе, используя формулу работы-энергии.
Когда покоящийся объект перемещается на определенное расстояние при приложении силы, он делает работу. Приложенная сила конвертирует скопленную потенциальную энергию недвижного объекта в кинетическую энергию для выполнения работы. Вот почему применяется формула работы-энергии; мы можем вычислить скорость по силе и массе.
формула работы является,
Так как работа объекта — это получение им кинетической энергии. ,
Мужик имеет горки массой 80 кг со скоростью 30 км / ч за 2 секунды, когда к нему прилагается сила 200 Н, когда он толкает горку на игровой площадке. Высчитайте скорость скольжения человека.
Данный:
Формула:
Решения:
Скорость скольжения человека рассчитывается при помощи формула работы-энергии в виде,
Но скорость v = d / t
Используя формулу работы и энергии, мы можем вычислить скорость в определениях силы, массы и скорости.
Подставляя все значения,
Скорость скольжения человека 25 м / сек.
Как высчитать скорость по силе и массе при помощи формулы мощности?
Давайте рассчитаем скорость по силе и массе, используя формулу мощности.
Мощность любого объекта измеряется количеством его работы, выполненной за единицу времени. Так как проделанная работа объекта является произведением приложенной силы и пройденного расстояния. Поэтому, используя формулу мощности, мы можем высчитать скорость объекта конкретно из приложенной силы и ее мощности.
формула мощности является,
Но работа изготовлена
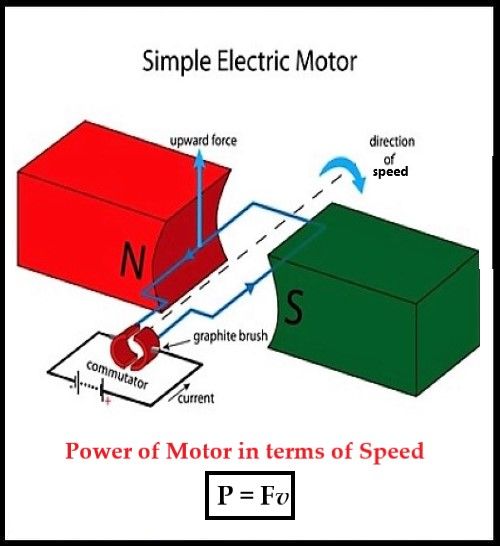
Как высчитать скорость по силе и массе при помощи формулы мощности
(Кредит: Shutterstock )
Если номинальная мощность мотора составляет 500 Вт, он может делать работу при приложении силы 80 Н. Какая скорость у мотора?
Данный :
Отыскать : v=?
Формула :
Решения :
Скорость рассчитывается с внедрением формула мощности,






