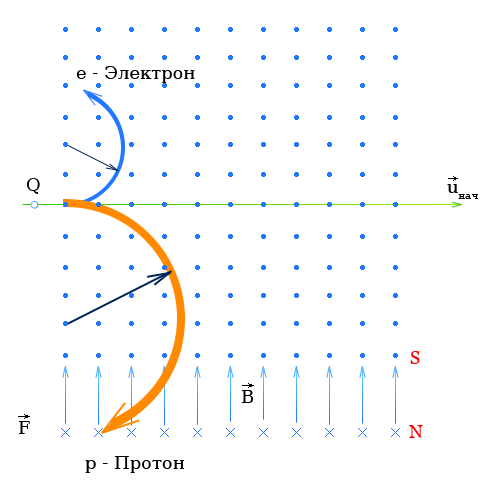
§ 19. Движение заряженных частиц в магнитном поле. Сила Лоренца
Сила Лоренца.
Значимый энтузиазм представляет движение заряженных частиц в области места, где сразу имеются электрическое и магнитное поля. Для этого варианта Лоренц получил выражение для силы, которую в честь него именуют силой Лоренца. Она представляет собой сумму сил, действующих на заряженную частичку, которая движется в электрическом и магнитном полях.
Пусть заряженная частичка с зарядом q движется со скоростью в однородном магнитном поле с индукцией и в однородном электрическом поле с напряжённостью . Электрическое поле действует на заряд q с силой, модуль которой равен Fэ = qE. Эта составляющая силы Лоренца получила название электрической составляющей. В магнитном поле на перемещающуюся частичку действует магнитная составляющая силы Лоренца.
Её модуль можно отыскать при помощи закона Ампера. Представим, что проводник с током находится в однородном магнитном поле. Вдоль проводника движутся заряженные частички. Разглядим отрезок проводника длиной Δl и площадью поперечного сечения S (рис. 3.38).
На него со стороны магнитного поля действует сила Ампера. В § 1 "Условия существования электрического тока. Электрический ток в проводниках" была выведена формула, определяющая силу тока в проводнике:
Подставив это выражение в формулу для модуля силы Ампера FA = BIΔlsin α, получим
где N = nSΔl — число заряженных частиц в рассматриваемом объёме SΔl. Магнитная составляющая силы Лоренца равна по модулю
где α — угол между векторами и .
Магнитная составляющая силы Лоренца всегда перпендикулярна плоскости, в какой размещаются вектор скорости заряженной частички и вектор индукции магнитного поля.
В силу того что данная сила перпендикулярна скорости частички, она не совершает работы.
Поэтому, если есть и электрическое поле, и магнитное, то полная сила , действующая на перемещающуюся частичку, равна
Для определения направления магнитной составляющей силы Лоренца применяют правило левой руки.
Если левую руку расположить так, дабы полосы магнитной индукции входили в ладонь, а четыре вытянутых пальца демонстрировали направление скорости движения положительно заряженной частички, то отогнутый (в плоскости ладошки) на 90° большой палец покажет направление действующей на заряженную частичку магнитной составляющей силы Лоренца.
Если в магнитном поле движутся негативно заряженные частички, то пальцы левой руки следует располагать обратно направлению вектора скорости. Для иллюстрации использования правила левой руки приведём набросок 3.39.
На нём штриховыми линиями указаны траектории перемещения зарядов (на рис. 3.39, а — положительного заряда, на рис. 3.39, б — отрицательного заряда).
Движение заряженной частички в однородном магнитном поле.
Разглядим более обычной случай движения заряженной частички в магнитном поле — это движение в однородном магнитном поле с индукцией, перпендикулярной исходной скорости частички (рис. 3.40).
Так как магнитное поле не изменяет модуля скорости заряженной частички, то остаётся постоянным и модуль магнитной составляющей силы Лоренца. Так как эта сила перпендикулярна скорости, то частичка движется с центростремительным ускорением. Неизменность по модулю центростремительного ускорения частички, перемещающейся с неизменной по модулю скоростью, значит, что радиус кривизны R линии движения частички постоянен. Частичка движется умеренно по окружности радиусом R. Согласно второму закону Ньютона,
Поэтому, измерив R при узнаваемых υ и В, мы можем найти удельный заряд разных частиц.
Масс-спектрограф.
C помощью магнитного поля можно делить заряженные частички по их удельным зарядам и точно определять массы частиц. Разделение частиц осуществляется в масс-спектрографах 1 .
1 Масс-спектрограф был в первый раз сконструирован в 1919 г. учеником Дж. Дж. Томсона — Франсисом Астоном (1877—1945). C помощью этого устройства он произвёл четкие измерения масс и изъянов масс ряда изотопов.
На рисунке 3.41, а изображена схема простого масс-спектрографа, а на рисунке 3.41, б — внешний облик современного устройства. Вакуумная камера масс-спектрографа помещена в магнитное поле (вектор магнитной индукции перпендикулярен рисунку). Ускоренные электрическим полем заряженные частички (электроны либо ионы), описав дугу, попадают на фотопластинку, где оставляют след, позволяющий с большой точностью измерить радиус линии движения R. По этому радиусу можно найти удельный заряд иона и, поэтому, его массу.
Циклотрон.
Используя формулу для радиуса линии движения, найдём время прохождения заряженной частичкой полуокружности:
т. е. Δt зависит только от параметров частички и индукции магнитного поля.
Данный факт был применен южноамериканским физиком Эрнестом Лоуренсом (1901 — 1958), который в 1931 г. сделал циклотрон. Это устройство позволяет ускорять заряженные частички сравнимо маленьким электрическим полем в течение ряда циклов. Разглядим устройство циклотрона (рис. 3.42).
Два электрода специальной формы — дуанты находятся в камере, где поддерживается вакуум (рис. 3.43).
Дуанты помещают между полюсами сильного магнита, и к ним подводится переменная разность потенциалов. В центре камеры между дуантами располагают источник заряженных частиц. В тот момент, когда между дуантами существует высочайшая разность потенциалов, электрическое поле в промежутке между ними ускоряет заряженные частички.
Ускоренные частички влетают во внутреннюю часть дуанта, где электрическое поле фактически отсутствует. Двигаясь под действием магнитной составляющей силы Лоренца по окружности, заряженные частички через половину оборота опять возникают в щели между дуантами.
Те из частиц, которые двигались с подходящей скоростью, пройдут через щель как раз в тот момент (через половину периода конфигурации приложенного к дуантам напряжения), когда там электрическое поле успеет поменять своё направление на обратное. Такие частички опять ускоряются, обрисовывают снутри другого дуанта полуокружность ещё большего радиуса и опять в нужный момент подходят к ускоряющему промежутку (время прохождения частичками полуокружности остаётся постоянным, так как оно не находится в зависимости от скорости частички) и т. д. Другие частички ускоряются некординально либо совершенно не ускоряются.
Циклотроны и другие более массивные ускорители заряженных частиц (к примеру, фазотроны, синхротроны, синхрофазотроны) находят обширное использование в ядерной физике и физике простых частиц. Изучая столкновения ускоренных частиц с частичками мишени, физики получают возможность изучить строение наночастиц, действующие между ними силы, обоюдные перевоплощения простых частиц.
Магнитный щит земли.
Магнитное поле Земли оказывает существенное воздействие на поток заряженных частиц из космоса (космические лучи). Оно образует 3-ий «защитный пояс» вместе с атмосферой и ионосферой, защищающий живы организмы на Земле от гибельного деяния космических лучей.
На большой высоте магнитное поле Земли невелико, но захватывает большенные области места. Действуя на заряженную частичку долгое время, оно значительно изменяет её линию движения. Заместо прямой полосы выходит спираль, навивающаяся на полосы индукции магнитного поля (рис. 3.44).
На летящую вдоль полосы магнитной индукции частичку сила Лоренца не действует. Вот почему частички свободно могут приближаться к полюсам, откуда веером расползаются полосы магнитной индукции.
Не считая того, магнитное поле Земли держит на большой высоте заряженные частички не очень огромных энергий. Эти области с завышенной концентрацией заряженных частиц, окружающих земной шар, именуют радиационными поясами. Большая часть частиц наружного радиационного пояса Земли составляют электроны, а её внутреннего радиационного пояса — протоны (рис. 3.45).
Протоны задерживаются более сильным магнитным полем во внутреннем радиационном поясе. В радиационных поясах заряженные частички движутся от 1-го полюса к другому, оставаясь в «магнитной ловушке».
Вопросы:
а) электрической составляющей силы Лоренца;
б) магнитной составляющей силы Лоренца?
2. В каком случае магнитная составляющая силы Лоренца будет наибольшей?
3. Как можно найти направление магнитной составляющей силы Лоренца, действующей:
а) на положительно заряженную частичку;
б) на негативно заряженную частичку?
4. Зачем применяют:
5. Как оказывает влияние магнитное поле Земли на потоки космических лучей?
Вопросы для обсуждения:
1. Действует ли магнитная составляющая силы Лоренца:
а) на незаряженную частичку в однородном магнитном поле;
б) на заряженную частичку, покоящуюся в магнитном поле;
в) на заряженную частичку, перемещающуюся вдоль линий магнитного поля?
2. Как будет двигаться положительно заряженная частичка в параллельных электрическом и магнитном полях, если её исходная скорость ориентирована под некоторым углом к и к ?
Пример решения задачи
Электрон влетает в однородное магнитное поле с индукцией 10 -3 Тл перпендикулярно линиям магнитной индукции и под углом α = π/4 к границе поля (рис. 3.46, а).
Модуль скорости электрона равен 10 6 м/с. В направлении осей X и Y магнитное поле беспредельно. На каком расстоянии от точки влёта электрон вылетит из поля? Отношение заряда электрона к его массе e/m = 1,76 ∙ 10 11 Кл/кг.
В магнитном поле под действием магнитной составляющей силы Лоренца электрон обрисует дугу окружности. Найдём её радиус R. Запишем 2-ой закон Ньютона:
Ответ: l = 8 мм.
Упражнения:
1. Протон в магнитном поле с индукцией 0,01 Тл обрисовал окружность радиусом 10 см. Чему равна скорость протона?
2. Найдите ускорение протона, который движется со скоростью 2 м/с в магнитном поле с индукцией 3 мТл перпендикулярно линиям магнитной индукции.
3. Обусловьте кинетическую энергию электрона, перемещающегося по окружности радиусом 1 см в однородном магнитном поле с индукцией 0,03 Тл. Приведите ответ в Дж и в эВ.
4. Протон с энергией 600 эВ влетает в однородное магнитное поле с индукцией 0,33 Тл перпендикулярно линиям магнитной индукции. Найдите радиус линии движения протона. Будет ли изменяться кинетическая энергия протона при движении в этом магнитном поле?
5. Электрон влетает в однородное магнитное поле с индукцией 9,4 мТл так, что вектор его скорости составляет угол 30° с направлением линий магнитной индукции (рис. 3.47).
Обусловьте радиус витков линии движения электрона и расстояние, пройденное им вдоль полосы магнитной индукции за три витка. Скорость электрона равна 2,5 ∙ 10 6 м/с.
6. Электрон, влетающий в однородное магнит ное поле под углом 60° к линиям магнитной индукции, движется по спирали поперечником 10 см с периодом воззвания 6 ∙ 10 -5 с. Обусловьте скорость электрона, индукцию магнитного поля и шаг спирали.
Движение электронов в магнитном поле
Цель работы. Определение удельного заряда электрона по известной линии движения пучка электронов в электрическом и переменном магнитном полях.
Приборы и принадлежности: экспериментальная установка марки «PHYWE» конторы HYWE Systems GmbH & Co. (Германия) в составе: электронно-лучевая трубка; катушки Гельмгольца (1 пара); источник питания универсальный (2 шт.); цифровой мультиметр (2 шт.); разноцветные соединительные шнуры.
Введение
Удельным зарядом простой частички именуют отношение заряда частички к её массе . Эта черта обширно применяется для идентификации частиц, так как позволяет отличать друг от друга различные частички, имеющие однообразные заряды (к примеру, электроны от негативно заряженных мюонов, пионов и др.).
Удельный заряд электронаотносится к базовым физическим неизменным, таким как заряд электронае, скорость света с, неизменная Планка h и др. Его теоретическое значение составляет величину = (1,75896 ± 0,00002)∙10 11 Кл∙кг -1 .
Бессчетные экспериментальные способы определения удельного заряда частиц основаны на исследовательских работах особенностей их движения в магнитном поле. Дополнительные способности представляет внедрение конфигурации магнитного и электрического полей и варьирование их характеристик. В данной работе определяется удельный заряд электрона на экспериментальной установке марки «PHYWE» германского производства. В ней для исследования траекторий движения электронов в магнитном поле реализован способ, основанный на сочетании способностей варьирования характеристик однородных магнитного и электрического полей при их взаимно перпендикулярной конфигурации. Данное методическое пособие создано с внедрением документации, поставленной в комплекте с установкой.
Магнитное поле. Опыты демонстрируют, что магнитное поле действует на перемещающиеся в нём заряженные частички. Силовой чертой, определяющей схожее его действие, является магнитная индукция – векторная величина В. Магнитное поле изображают при помощи силовых линий магнитной индукции, касательные к которым в каждой точке совпадают с направлением вектора B. При однородном магнитном поле вектор B постоянен по величине и направлению в хоть какой точке поля. Сила, действующая на заряд q, перемещающийся со скоростью V в магнитном поле, была определена германским физиком Г. Лоренцем (сила Лоренца). Она выражается формулой
Fл = q∙[ V∙B] либо Fл = |q|VB∙sinα (1)
где α – угол, образованный вектором скорости V перемещающейся частички и вектором индукции магнитного поля В.
На недвижный электрический заряд магнитное поле не действует. В этом его существенное отличие от поля электрического.
Направление силы Лоренца определяется при помощи правила «левой руки». Если ладонь левой руки расположить так, дабы в неё заходил вектор B, а четыре вытянутых пальца навести вдоль
направления движения положительных зарядов (q>0), совпадающие с направлением тока I (), то отогнутый большой палец
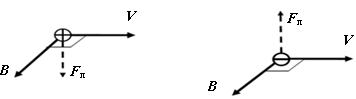
Рис.1
покажет направление силы, действующей на положительный заряд (q>0) (рис. 1). В случае отрицательных зарядов (q<0) направления тока I и скорости V движения обратны. Направление силы Лоренца определяется по направлению тока. Таким макаром, сила Лоренца перпендикулярна вектору скорости, потому модуль скорости не будет изменяться под действием этой силы. Но при неизменной скорости, Как видно из формулы (1), остаётся неизменным и значение силы Лоренца. Из механики понятно, что неизменная сила, перпендикулярная скорости, вызывает движение по окружности, другими словами является центростремительной. При отсутствии других сил, согласно второму закону Ньютона, она докладывает заряду центростремительное либо обычное ускорение . Траектория перемещения заряда в однородном магнитном поле приVB представляет собой окружность (рис.2), радиус которой r определяется из условия
, (2)
где α – угол между векторами V и B.
В случае α = 90 0 , sinα = 1 из формулы (2) радиус радиальный линии движения заряда определяется формулой
(3)
Работа, совершаемая над перемещающейся зарядом в магнитном поле неизменной силой Лоренца, равна
ΔА = Fл.Δr
либо ΔА = Fл.Δr cosβ, (4)
где β – угол между направлением векторов силы Fл. и направлением вектора перемещения Δr.
Так как обычно осуществляется условие Fл Δr, β = 90 0 и cosβ = 0, то работа, совершаемая силой Лоренца, Как видно из (4), всегда равна нулю. Поэтому, абсолютное значение скорости заряда и его кинетическая энергия при движении в магнитном поле остаются неизменными.
Период вращения (время 1-го полного оборота), равен
(5)
Подставив в (5) заместо радиуса r его выражение из (3), получим, что кругообразное движение заряженных частиц в магнитном поле обладает принципиальной особенностью: период воззвания не находится в зависимости от энергии частички, зависит только от индукции магнитного поля и величины, оборотной удельному заряду:
. (6)
Если магнитное поле однородно, но исходная скорость заряженной частички V ориентирована под углом α к силовым линиям В, то движение можно представить как суперпозицию 2-ух движений: равномерного прямолинейного в направлении, параллельном магнитному полю со скоростью V// = V∙cosα и равномерного
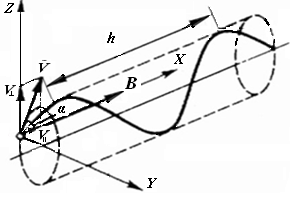
вращения под действием силы Лоренца в плоскости, перпендикулярной магнитному полю cо скоростью V┴ = V∙sinα.
В итоге траектория перемещения частички будет представлять собой винтообразную линию (рис.3).
Шаг винтообразной полосы равен расстоянию, пройденному зарядом вдоль поля со скоростью V// за время, равное периоду вращения
h = VТcos, (7)
где .
Подставив это выражение для Т в (7), получим
. (8)
Ось спирали параллельна силовым линиям магнитного поля B.
Электрическое поле. На точечный заряд q, помещённый в электрическое поле, характеризующееся вектором напряжённости E, действует сила
F = qE, (9)
Направление силы F совпадает с направлением вектора E, если заряд положительный, и обратно E в случае отрицательного заряда. В однородном электрическом поле вектор напряжённости в хоть какой точке поля постоянен по величине и направлению. Если движение происходит только вдоль силовых линий однородного электрического поля, оно является равноускоренным прямолинейным.
По второму закону Ньютона F = ma уравнение движения заряда в электрическом поле выражается формулой
qE = (10)
Представим, что точечный отрицательный заряд, двигающийся сначало вдоль оси Х со скоростью V, попадает в однородное электрическое поле между пластинами плоского конденсатора, как показано на рис. 4.
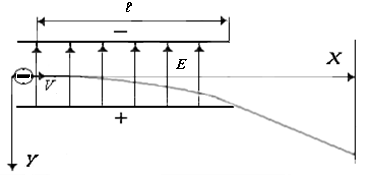
Движение заряда вдоль оси X является равномерным, его кинематическое уравнение x = x0 + Vt (x0 – исходная координата, t – время), V = const, x0 = 0. Время пролёта зарядом конденсатора с длиной пластинок ℓ равно .
Движение вдоль оси Y определяется электрическим полем снутри конденсатора. Если зазор между пластинами мал по сопоставлению с их длиной, краевыми эффектами можно пренебречь и электрическое поле в пространстве между пластинами считатьоднородным (Еy = const). Движение заряда будет равноускоренным Vy = V0y + at. Ускорение определяется с формулой (10). Выполнив интегрирование (10), получим ,где С − неизменная интегрирования. При исходном условии (t = 0) V0y = 0 получим C = 0. .
Линия движения и нрав движения заряженной частички в однородном электрическом поле плоского конденсатора подобны аналогичным чертам движения в гравитационном поле брошенного горизонтально тела. Отклонение заряженной частички вдоль оси Y равно . С учётом нрава действующей силы оно зависит отсогласно формуле.
При перемещении заряда в электрическом поле между точками, имеющими разность потенциалов U, электрическим полем совершается работа, вследствие чего заряд приобретает кинетическую энергию. В согласовании с законом сохранения энергии
.
Если на перемещающийся электрический заряд кроме магнитного поля с индукцией В действует и электрическое поле с напряжённостью E, то результирующая сила F, определяющая его движение, равна векторной сумме силы, действующей со стороны электрического поля и силы Лоренца
Fэм = qE + q[V∙B]. (11)
Это выражение именуется формулой Лоренца.
В данной лабораторной работе исследуется движение электронов в магнитном и электрическом полях. Все соотношения, рассмотренные выше для случайного заряда, справедливы и для электрона.
Считаем, что исходная скорость электрона приравнивается нулю. Попадая в электрическое поле, заряд ускоряется в нём, и, пройдя разность потенциалов U, приобретает некоторую скорость V. Её можно найти из закона сохранения энергии. В случае нерелятивистских скоростей (V << скорости света c) имеющего вид
, (12)
где е = –1,6∙10 -19 Кл – заряд электрона, me = 9,1∙10 -31 кг – его масса.
Из (12) скорость электрона
.
Подставляя её в (3), получим формулу для нахождения радиуса окружности, по которой движется электрон в магнитном поле:
. (13)
Таким макаром, зная разность потенциалов U, ускоряющую электроны при их движении в электрическом поле до нерелятивистских скоростей, индукцию однородного магнитного поля B, в каком эти электроны движутся, описывая радиальную линию движения, и, экспериментально определяя радиус обозначенной радиальный линии движения r, можно вычислить удельный заряд электрона по формуле
(14)
Формула силы Лоренца
Сила $\bar$ , действующая на перемещающуюся заряженную частичку в магнитном поле, равная:
именуется силой Лоренца (магнитной силой).
Исходя из определения (1) модуль рассматриваемой силы:
$$F=q v B \sin \alpha(2)$$
где $\bar$ – вектор скорости частички, q – заряд частички, $\bar$ – вектор магнитной индукции поля в точке нахождения заряда, $\alpha$ – угол между векторами $\bar$ и $\bar$. Из выражения (2) следует, что если заряд движется параллельно силовым линиям магнитного поля,то сила Лоренца равна нулю. Время от времени силу Лоренца стараясь выделить, обозначают, используя индекс: $\bar_L$
Направление силы Лоренца
Сила Лоренца (как и всякая сила) – это вектор. Ее направление перпендикулярно вектору скорости $\bar$ и вектору $\bar$ (другими словами перпендикулярно плоскости, в какой находятся векторы скорости и магнитной индукции) и определяется правилом правого буравчика (правого винта) рис.1 (a). Если мы имеем дело с отрицательным зарядом, тонаправление силы Лоренца обратно результату векторного произведения (рис.1(b)).
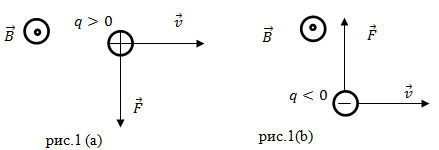
вектор $\bar$ ориентирован перпендикулярно плоскости рисунков на нас.
Следствия параметров силы Лоренца
Так как сила Лоренца ориентирована всегда перпендикулярно направлению скорости заряда, то ее работа над частичкой равна нулю. Выходит, что воздействуя на заряженную частичку с помощью неизменного магнитного поля нельзя поменять ее энергию.
Если магнитное поле однородно и ориентировано перпендикулярно скорости движения заряженной частички, то заряд под воздействием силы Лоренца будет передвигаться по окружности радиуса R=const в плоскости, которая перпендикулярна вектору магнитной индукции. При всем этом радиус окружности равен:
где m – масса частички,|q|- модуль заряда частички, $\gamma=\frac>>>>$ – релятивистский множитель Лоренца, c – скорость света в вакууме.
Сила Лоренца — это центростремительная сила. По направлению отличия простой заряженной частички в магнитном поле делают вывод о ее знаке (рис.2).
Формула силы Лоренца при наличии магнитного и электрического полей
Если заряженная частичка перемещается в пространстве, в каком находятся сразу два поля (магнитное и электрическое), то сила, которая действует на нее, равна:
где $\bar$ – вектор напряженности электрического поля в точке, в какой находится заряд. Выражение (4) было эмпирически получено Лоренцем. Сила $\bar$, которая заходит в формулу (4) так же именуется силой Лоренца (лоренцевой силой). Деление лоренцевой силы на составляющие: электрическую $(\bar = q \bar)$ и магнитную $(\bar=q[\bar \times \bar])$ относительно, так как связано с выбором инерциальной системы отсчета. Так, если система отсчета будет двигаться с таковой же скоростью $\bar$, как и заряд, то в таковой системе сила Лоренца, действующая на частичку, будет равна нулю.
Единицы измерения силы Лоренца
Основной единицей измерения силы Лоренца (как и хоть какой другой силы) в системе СИ является: [F]=H
Примеры решения задач
Задание. Какова угловая скорость электрона, который движется по окружности в магнитном поле с индукцией B?
Решение. Так как электрон (частичка имеющая заряд) совершает перемещение в магнитном поле, то на него действует сила Лоренца вида:
где q=qe – заряд электрона. Так как в условии сказано, что электрон движется по окружности, то это значит, что $\bar \perp \bar$, поэтому, выражение для модуля силы Лоренца воспримет вид:
Сила Лоренцаявляется центростремительной и не считая того, по второму закону Ньютона будет в нашем случае равна:
Приравняем правые части выражений (1.2) и (1.3), имеем:
Из выражения (1.3) получим скорость:
Период воззвания электрона по окружности можно отыскать как:
Зная период, можно отыскать угловую скорость как:
Ответ. $\omega=\frac B>$

испытанных создателя готовы посодействовать в написании работы хоть какой трудности
Мы посодействовали уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Выясни цена собственной работы за 15 минут!
Задание. Заряженная частичка (заряд q, масса m) со скоростью vвлетает в область, где имеется электрическое поле напряженностью E и магнитное поле с индукцией B. Векторы $\bar$ и $\bar$ совпадают по направлению. Каково ускорение частички в моментначалаперемещения в полях, если $\bar \uparrow \bar \uparrow \bar$?
Решение. Создадим набросок.
На заряженную частичку действует сила Лоренца:
Магнитная составляющая имеет направление перпендикулярное вектору скорости ($\bar$) и вектору магнитной индукции ($\bar$). Электрическая составляющая сонаправлена с вектором напряжённости ($\bar$) электрического поля. В согласовании со вторым законом Ньютона имеем:
Получаем, что ускорение равно:
Если скорость заряда параллельна векторам $\bar$ и $\bar$, тогда $[\bar \times \bar]=0$, получим: