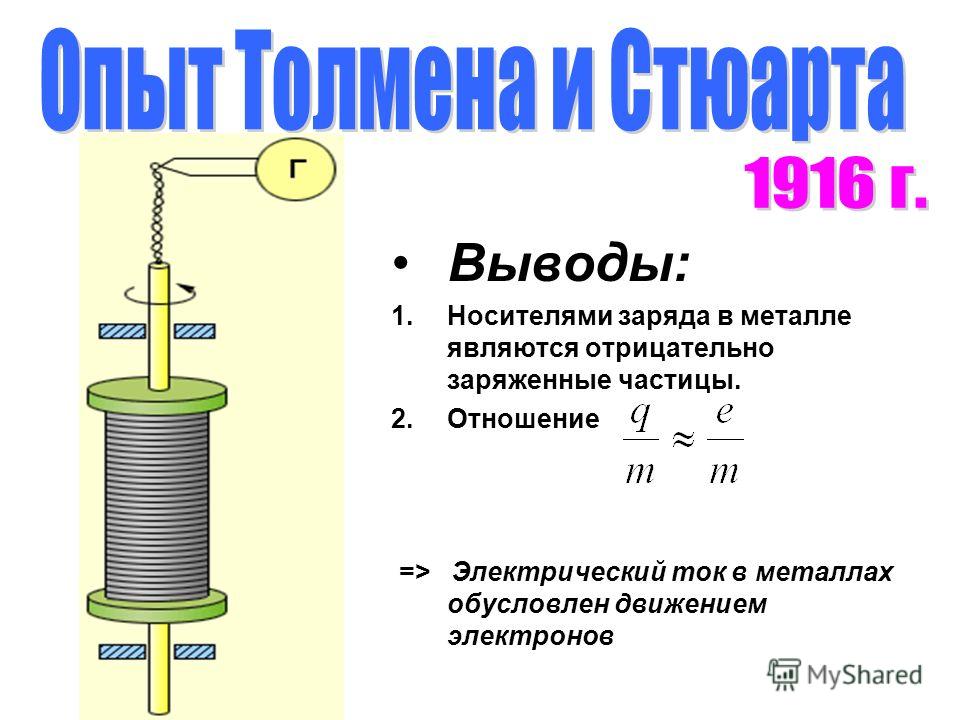
Электрический ток в металлах носители заряда

Электрический ток в металлах — это упорядоченное (направленное) движение электронов под действием электрического поля.

Особенность железных проводников заключается в том, что заряд электричества переносят свободные электроны. Они передвигаются в одном направлении под воздействием наружного электрического поля, создавая электрический ток.

Природа электрической проводимости у металлов обоснована наличием кристаллической решётки, в узлах которой размещены положительные ионы, а в пространстве между ними движутся свободные электроны. Свободные электроны не связаны с ядрами собственных атомов. Отрицательный заряд всех свободных электронов по модулю равен положительному заряду всех ионов решетки, таким макаром проводник считается электрически нейтральным.

Кто открыл, опыт Мандельштама и Папалекси

1-ые опыты по исследованию электрической проводимости металлов провел германский ученый Карл Виктор Эдуард Рикке в 1901 году. Сущность опыта сводилась к следующему. Три отполированных цилиндра плотно придавили друг к другу, расположив в таком порядке: медь–алюминий–медь. В течение года через них пропускали ток в одном и том же направлении.

Суммарный заряд, прошедший через этот проводник за всегда составил более 3,5 МКл. После окончания опыта цилиндры взвесили и выяснилось, что их массы не поменялись. Это исследование стало подтверждением того, что прохождение тока в металлах не связано с хим процессами и переносом вещества, а заряд создается частичками, которые имеются у всех металлов, т.е. электронами.

Опыты по исследованию электропроводимости в 1916 году продолжили российские Исследователи Л. И. Мандельштам и Н. Д. Папалекси. Они задались целью выяснить, имеется ли масса у электрона. Если электрон обладает массой, то должен подчиняться законам механики, в том числе, закону инерции. Например, если перемещающийся проводник резко приостановить, то электроны еще какое-то время будут двигаться в том же направлении по инерции.

Была собрана такая установка: катушка на стержне со скользящими контактами, которые присоединены к гальванометру. Катушка крутилась с большой скоростью, потом резко останавливалась, при всем этом фиксировали отклонение стрелки гальванометра. В процессе опыта Исследователи установили, что электрон обладает массой. Но измерить эту массу они не смогли, опыт был только высококачественным.

Спустя три года физики Р. Толмен и Б. Стюарт предложили свой вариант подобного опыта, что позволило произвести количественные измерения. Им удалось вычислить массу электрона. Для этого они измерили заряд на выходах катушки, образующийся при торможении. После неожиданной остановки катушки в цепи появлялся импульс тока. Направление тока указывало на то, что он вызван движением отрицательных зарядов.

При помощи баллистического гальванометра Исследователи измерили суммарный заряд, проходящий по цепи, и вычислили отношение заряда одной частички к ее массе — q / m . Оно оказалось близким по значению к отношению e / m для электрона = 1 , 8 × 1011 К л / к г , которое на тот момент уже было понятно.

Какие частички его делают, скорость распространения тока

Отменная электропроводность металлов обоснована высочайшей концентрацией свободных электронов. Каждый атом металла, находящийся в узле кристаллической решетки, имеет один либо несколько валентных (свободных) электронов. Валентные электроны находятся на наружной электронной оболочке и слабо связаны с ядром, потому атом просто с ними расстается.

Они совершают термическое движение в разных направлениях по всему кристаллу. Положительные ионы остаются в узлах кристаллической решетки, а место между ними заполняется свободными электронами либо так именуемым электронным газом.

Если железный проводник присоединить к источнику тока и замкнуть цепь, валентные электроны продолжают совершать хаотическое движение, но под действием появившегося наружного электрического поля они также начинают передвигаться в одном направлении. Это упорядоченное течение электронного газа, совмещенное с термическим движением электронов, и есть электрический ток в металле.

Скорость упорядоченного движения (дрейфовая скорость) любого электрона в проводнике не превосходит 1 мм/с.

Скорость распространения электрического тока близка к скорости света в вакууме (300 000 км/с).

Сразу с распространением электрического поля все электроны начинают двигаться в одном направлении по всей длине проводника.

Закон Ома и Джоуля-Ленца, формулы

Традиционная электронная теория металлов берет за базу, что движение электронов подчиняется законам механики Ньютона. При всем этом не учитывают взаимодействие электронов между собой. Подразумевается также, что при каждом столкновении с положительными ионами электрон передает решетке всю полученную в электрическом поле энергию, а потом начинает движение с нулевой дрейфовой скоростью.

Невзирая на эти особенности, законы электрического тока в железных проводниках — Ома и Джоуля–Ленца — находятся в пределах традиционной электронной теорией.

Закон Ома

В 1827 году германский физик Георг Ом установил, что связь таких физических черт, как сила тока, напряжение и сопротивление определяется следующей зависимостью: для определенного участка цепи сила тока I прямо пропорциональна напряжению U и назад пропорциональна электрическому сопротивлению R.

Закон Джоуля–Ленца

Так как проводник греется при протекании по нему электрического тока, то выделяется теплота. В 1841–1842 годах сходу два ученых независимо друг от друга Дж. Джоуль (Великобритания) и Э. Х. Ленц (Наша родина) экспериментально обосновали, что количество выделяющейся теплоты Q прямо пропорционально квадрату тока I2, сопротивлению проводника R и времени t, в течение которого ток протекал по проводнику.

Q=I2Rt.

Проводник греется за счет работы сил электрического поля над носителями заряда. Эта работа A также равна Q: A=Q=I2Rt.

Применив закон Ома для участка однородной цепи и определение силы тока, можно получить следующие варианты формулы:

ЭЛЕКТРИЧЕСКИЙ ТОК В Разных СРЕДАХ

1. Мы уже воспользовались представлением о том, что проводимость металлов обоснована наличием свободных электронов, которые могут просто передвигаться между ионами, находящимися в узлах кристаллической решетки. Ознакомимся на данный момент с тестами, лежащими в базе этих представлений.

1-ые опыты были проведены Э. Рикке в 1901 г. Три цилиндра — два медных и один дюралевый — с отлично отшлифованными торцами ставились друг на друга и присоединялись к источнику тока. В течение года по проводникам протекал ток порядка 0,1 А, так что общий заряд, прошедший через проводники, превысил 3,5 • 10 6 Кл. Все же никаких хим изменений в проводниках не вышло. Отсюда следует, что ток в металлах обоснован движением частиц, не имеющих дела к хим структуре металлов. Этими частичками, естественно, не могут быть ионы, которые у различных веществ различны, а могут быть только электроны.

2. Решающий опыт поставили в 1916 г. Т. Стюарт и Р. Толмен, измерив удельный заряд частиц (так именуется отношение заряда частички к массе самой частички q/m), осуществляющих проводимость в металлах. Сущность опыта заключалась в следующем. На катушку наматывался длиннющий проводник, присоединенный к гальванометру (рис. 10.1). Катушка приводилась в резвое вращение и потом резко тормозилась.

В процессе торможения свободные частички, находившиеся в металле, передвигались в направлении движения проводника аналогично тому, как перемещается вперед пассажир при резком торможении вагона. При всем этом в проводнике появлялся ток, направление которого зависело от знака этих частиц.

3. Опыт показал, что свободные частички, осуществляющие проводимость в металлах, заряжены негативно. Их удельный заряд оказался равным у меди 1,60- 10" Кл/кг, у серебра 1,49- 10" Кл/кг, у алюминия 1,54-10" Кл/кг. Как уже было понятно, удельный заряд электрона

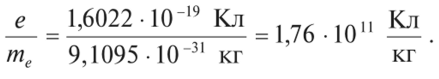
Как видно, погрешность опыта лежит в границах 9—15 %, что для таких сложных опытов является неплохим результатом. Это позволяет с достаточной уверенностью утверждать, что электрический ток в металлах есть итог упорядоченного движения свободных электронов.

• 4. На этой базе мы можем разъяснить три принципиальных эффекта.
• 1. Работа выхода в вакууме.

Электроны, перемещающиеся снутри металла, могут время от времени вылететь за его пределы, образуя над ним «электронное облако». Часть этих электронов вновь ворачивается в металл, другие опять его покидают. Это явление очень похоже на испарение жидкостей. Поверхность металла и электронное скопление образуют двойной электрический слой, аналогичный плоскому конденсатору. Толщина этого слоя равна нескольким межатомным расстояниям (d= 10 -10 — 10 -9 м). Разность потенциалов в этом слое именуют контактной разностью потенциалов между металлом и вакуумом.

Для оценки этой величины проделаем следующий приблизительный расчет. Представим для себя, что электрон вылетел из металла; тогда в последнем возникнет положительный заряд, равный по модулю заряду электрона. Этот положительный заряд именуют «электрическим изображением» электрона (рис. 10.2). Оказывается, что взаимодействие электрона с металлом равно взаимодействию между электроном и его «изображением», т. е. сводится к взаимодействию точечных зарядов, которое мы умеем рассчитывать. Согласно (8.14), для контактной разности потенциалов (при d* 5 • КГ 10 м) имеем

Для того дабы электрон, находящийся в металле, мог выйти за его пределы, он должен совершить работу против сил притяжения от собственного «изображения» и против сил отталкивания от негативно заряженного электронного облака. Эту работу именуют работой выхода. Работа выхода, таким макаром, равна той малой энергии, которую необходимо сказать электрону проводимости, дабы он мог выйти из металла в вакуум. Можно положить, что работа выхода

Приблизительный расчет дает для работы выхода значение А0» 1,5 эВ = 2,4 • КГ 19 Дж, что по порядку величины совпадает с плодами, приобретенными в опыте.

2. Контактная разность потенциалов

Разглядим сейчас границу контакта между 2-мя металлами с разной концентрацией электронов я, и п2 п2; поэтому, 2-ой металл приобретает больше электронов, чем он передаст первому.