Исследование закона ома для полной цепи

Цель работы: найти внутреннее сопротивление источника тока и его ЭДС.

Оборудование: источник питания, проволочный резистор, амперметр, ключ, вольтметр, соединительные провода.
Пояснения к работе

Электрический ток в проводниках вызывают так именуемые источники неизменного тока. Силы, вызывающие перемещение электрических зарядов снутри источника неизменного тока против направления деяния сил электростатического поля, именуются посторонними силами. Отношение работы Астор., совершаемой посторонними силами по перемещению заряда Q вдоль цепи, к значению этого заряда именуется электродвижущей силой  источника (ЭДС):

ЭДС источника измеряется вольтметром, сила тока – амперметром.

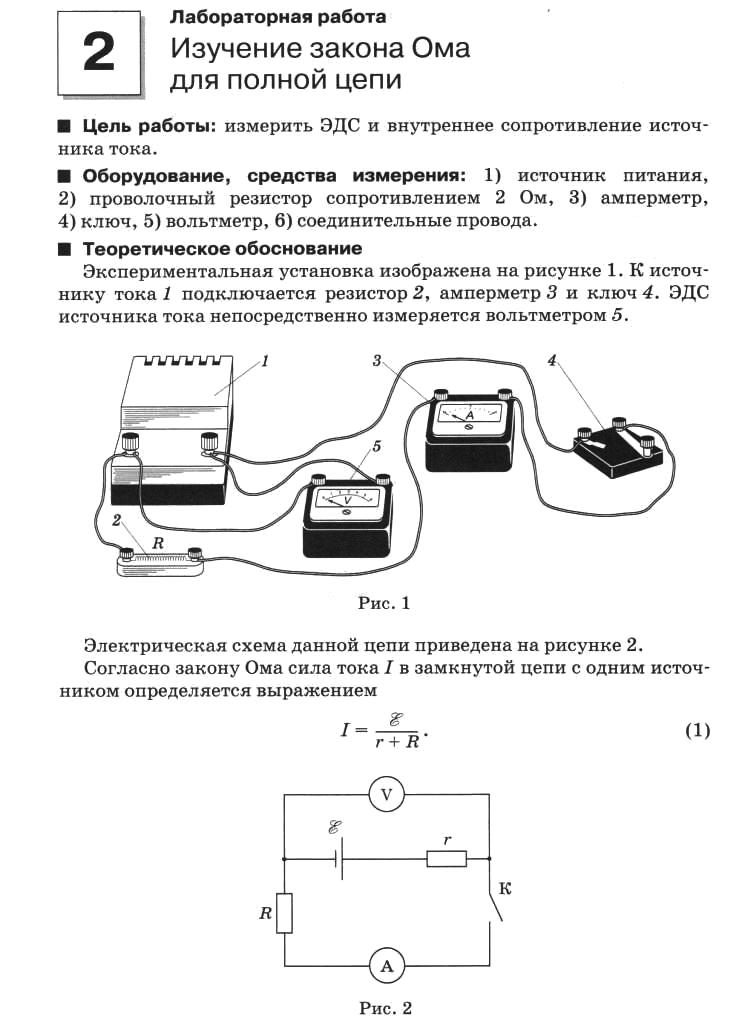
Согласно закону Ома сила тока в замкнутой цепи с одним источником определяется выражением:

Таким макаром, сила тока в цепи равна отношению электродвижущей силы источника к сумме сопротивлений наружного и внутреннего участков цепи. Пусть известны значения сил токов I1 и I2 и падения напряжений на реостате U1 и U2. Для ЭДС можно записать:
= I1(R1 + r) и

Приравнивая правые части этих 2-ух равенств, получим

Т.к. I1 R1 = U1 и I2 R2 = U2, то можно последнее равенство записать так

1. Без помощи других изучите методическое указание по выполнению лабораторной работы.
2. Соберите электрическую цепь по схеме, изображенной на рисунке. Установите сопротивление реостата 7 Ом, ЭДС батарейки 1,5 В, внутреннее сопротивление батарейки 3 Ом.

1. С помощью мультиметра обусловьте напряжение на батарейке при разомкнутом ключе. Это и будет ЭДС батарейки
2. =U.
3. Замкните ключ и определите силу тока I1 и напряжение U1 на реостате. Запишите показания устройств.
4. Измените сопротивление реостата и запишите другие значения силы тока I2 и напряжения U2.
5. Повторите измерения силы тока и напряжения еще для 4 разных положений ползунка реостата и запишите приобретенные значения в таблицу:

1. Высчитайте внутреннее сопротивление по формуле:

1. Обусловьте абсолютную и относительную погрешность измерения ЭДС (∆ℇ и δ
2. ) и внутреннего сопротивления (∆r и δr) батарейки.
3. Подготовьте отчет, он должен содержать: наименование темы и цели работы, список нужного оборудования, формулы разыскиваемых величин и их погрешностей, таблицу с плодами измерений и вычислений, вывод по работе.
4. Устно ответьте на контрольные вопросы.

1. Сформулируйте закон Ома для полной цепи.
2. Чему равна ЭДС источника при разомкнутой цепи?
3. Чем обосновано внутреннее сопротивление источника тока?
4. Чем определяется сила тока недлинного замыкания батарейки?

1. Дмитриева В. Ф. Физика для профессий и специальностей технического профиля: учебник для образовательных учреждений нач. и сред. проф. образования. — М.: Издательский центр «Академия», 2014;
2. Самойленко П.И. Физика для профессий и специальностей социально-экономического профиля: учебник для образовательных учреждений исходного и среднего проф. образования. — М.: Издательский центр «Академия», 2013;
3. Касьянов В.Д.Тетрадь для лабораторных работ. 10 класс.- М.: Дрофа, 2014.

Работа рассчитана на 2 часа

Лабораторная работа № 8

Тема: Определение ЭДС и внутреннего сопротивления источника напряжения

Цель работы: измерить ЭДС и внутреннее сопротивление источника тока.

Оборудование: источник питания, проволочный резистор, амперметр, ключ, вольтметр, соединительные провода.

Пояснения к работе

Схема электрической цепи показана на рисунке 1. В качестве источника тока в схеме применяется аккумулятор либо батарейка.

При разомкнутом ключе ЭДС источника тока равна напряжению на наружной цепи. В опыте источник тока замкнут на вольтметр, сопротивление которого должно быть много больше внутреннего сопротивления источника тока r. Обычно сопротивление источника тока не достаточно, потому для измерения напряжения можно применять вольтметр со шкалой 0–6 В и сопротивлением Rв = 900 Ом. Так как сопротивление источника обычно не достаточно, то вправду Rв r. При всем этом отличие Е от U на превосходит 10-х толикой процента, потому погрешность измерения ЭДС равна погрешности измерения напряжения.

Внутреннее сопротивление источника тока можно измерить косвенно, сняв показания амперметра и вольтметра при замкнутом ключе.

Вправду, из Закона Ома для замкнутой цепи получаем: Е=U+Ir, где U=IR – напряжение на наружной цепи. Потому

1. Без помощи других изучите методическое указание по выполнению лабораторной работы.
2. Соберите электрическую цепь согласно рисунку 1.
3. Определите вольтметром ЭДС источника тока при разомкнутом ключе:

1. Запишите класс точности вольтметра kv и предел измерения Umax его шкалы.
2. Найдите абсолютную погрешность измерения ЭДС источника тока:

1. Запишите окончательный итог измерения ЭДС источника тока:

1. Отключите вольтметр. Замкните ключ. Определите амперметром силу тока I в цепи.
2. Запишите класс точности амперметра kА и предел измерения Imax его шкалы.
3. Найдите абсолютную погрешность измерения силы тока:

1. Высчитайте внутреннее сопротивление источника тока по формуле:

1. Беря во внимание, что сопротивление резистора понятно с относительной погрешностью 3%, т.е. , оцените абсолютную погрешность его измерения:

1. Найдите абсолютную погрешность измерения внутреннего сопротивления источника тока:

1. Запишите окончательный итог измерения внутреннего сопротивления источника тока:

1. Результаты измерений и вычислений внесите в таблицу:

1. Подготовьте отчет, он должен содержать: наименование темы и цели работы, список нужного оборудования, формулы разыскиваемых величин и их погрешностей, таблицу с плодами измерений и вычислений, вывод по работе.
2. Устно ответьте на контрольные вопросы.

1. Почему показания вольтметра при разомкнутом и замкнутом ключе различны?
2. Как повысить точность измерения ЭДС источника тока?
3. Какое сопротивление именуют внутренним сопротивлением?
4. От чего зависит разность потенциалов между полюсами источника тока?

1. Дмитриева В. Ф. Физика для профессий и специальностей технического профиля: учебник для образовательных учреждений нач. и сред. проф. образования. — М.: Издательский центр «Академия», 2014;
2. Самойленко П.И. Физика для профессий и специальностей социально-экономического профиля: учебник для образовательных учреждений исходного и среднего проф. образования. — М.: Издательский центр «Академия», 2013;
3. Касьянов В.Д.Тетрадь для лабораторных работ. 10 класс.- М.: Дрофа, 2014.

Работа рассчитана на 2 часа

Лабораторная работа № 9

Тема: Исследование явления электромагнитной индукции

Цель работы: изучить явление электромагнитной индукции и характеристики вихревого электрического поля, установить и сконструировать правило определения индукционного тока.

Оборудование: миллиамперметр, катушка-моток, магнит дугообразный, источник питания, катушка с стальным сердечником от разборного электромагнита, ключ, соединительные провода.

Пояснения к работе

Электромагнитной индукцией именуется появление электродвижущей силы в проводнике при его перемещении в магнитном поле в замкнутом проводящем контуре вследствие его движения в магнитном поле либо конфигурации самого поля. Эта электродвижущая сила именуется электродвижущей силой электромагнитной индукции. Под ее воздействием в замкнутом проводнике появляется электрический ток, именуемый индукционным током.

Закон электромагнитной индукции (закон Фарадея-Максвелла): ЭДС электромагнитной индукции в контуре пропорционально и обратно по знаку скорости конфигурации магнитного потока через поверхность, натянутую на контур:

1. Без помощи других изучите методическое указание по выполнению лабораторной работы.
2. Подключите катушку-моток к зажимам миллиамперметра.
3. Следя за показаниями миллиамперметра, подводите один из полюсов магнита к катушке, позже на несколько секунд остановите магнит, а потом вновь приближайте его к катушке, вдвигая в нее.
4. Запишите, изменялся ли магнитный поток, пронизывающий катушку, во время движения магнита? Во время его остановки?
5. На основании ваших ответов на предшествующий вопрос сделайте и запишите вывод о том, при каком условии в катушке появляется индукционный ток.
6. О направлении тока в катушке можно судить по тому, в какую сторону от нулевого деления отклоняется стрелка миллиамперметра. Проверьте, одинаковым либо разным будет направление индукционного тока в катушке при приближении к ней и удалении от нее 1-го и такого же полюса магнита.
7. Приближайте полюс магнита к катушке с таковой скоростью, дабы стрелка миллиамперметра отклонялась менее чем на одну вторую предельного значения его шкалы.
8. Повторите тот же опыт, но при большей скорости движения магнита, чем в первом случае. При большей либо наименьшей скорости движения магнита относительно катушки магнитный поток, пронизывающий эту катушку, изменяется резвее? При резвом либо неспешном изменении магнитного потока через катушку в ней появлялся больший по модулю ток? На основании вашего ответа на последний вопрос сделайте и запишите вывод о том, как зависит модуль силы индукционного тока, возникающего в катушке, от скорости конфигурации магнитного потока, пронизывающего эту катушку.
9. Соберите электрическую цепь:

1. Проверьте, появляется ли в катушке-мотке 1 индукционный ток в следующих случаях:

б) при протекании через катушку 2 неизменного тока;

в) при увеличении и уменьшении силы тока, протекающего через катушку 2 методом перемещения в подобающую сторону движка реостата.

11. В каких из перечисленных в пт 9 случаях изменяется магнитный поток, пронизывающий катушку 1? Почему он изменяется?

12. Подготовьте отчет, он должен содержать: наименование темы и цели работы, список нужного оборудования, схемы опытов, вывод по работе.

Лабораторная исследование закона ома для полной цепи. Цель работы: углубление осознания закона Ома для полной цепи и для участка цепи. Пример решения задачи

1 3 Цель работы: углубление осознания закона Ома для полной цепи и для участка цепи. Задачка: экспериментально убедиться в справедливости закона Ома для замкнутой неразветвленной цепи. Приборы и принадлежности: модернизированная установка FPМ-0. ОБЩИЕ ВОПРОСЫ Электрическим током именуют упорядоченное движение электрических зарядов. Чертами тока являются сила тока I и плотность тока j. Сила тока скалярная величина и равна количеству электричества (заряда) dq, переносимого через сечение проводника за единицу времени: dq I. () dt Плотностью тока именуют количество электричества, пересекающее единицу площади поперечного сечения проводника в единицу времени: di j. () ds Плотность тока векторная величина, направленная вдоль вектора средней скорости упорядоченного движения положительных зарядов, и может быть записана как j q 0 n v, (3) где q 0 заряд единичного носителя тока; n концентрация носителей; v скорость дрейфа носителей. Если элемент поверхности ds рассматривать как вектор, направленный вдоль положительной нормали, то связь между силой тока и его плотностью имеет вид I (S) j ds, (4) где S площадь, через которую проходит поток заряженных частиц. Можно указать на ряд причин, способных вызвать упорядоченное движение зарядов. Сначала, это могут быть электрические (кулоновские) силы, под действием которых положительные заряды станут дви-

2 4 гаться вдоль силовых линий поля, отрицательные против. Поле этих сил именуют кулоновским, напряженность этого поля обозначим Е кул. Не считая того, на электрические заряды могут действовать и неэлектрические силы, к примеру, магнитные. Действие этих сил аналогично действию некоторого электрического поля. Назовем эти силы посторонними, а поле этих сил посторонним полем с напряженностью Е стор. В конце концов, упорядоченное движение электрических зарядов может появиться и без деяния наружных сил, а за счет явления диффузии либо за счет хим реакций в источнике тока. Работа, имеющая место при упорядоченном движении электрических зарядов, совершается за счет внутренней энергии источника тока. И хотя тут нет прямого деяния каких-то сил на свободные заряды, явление протекает так, будто бы на заряды действует некоторое постороннее поле. Важным законом электродинамики является закон Ома, установленный экспериментально. Но его можно получить на теоретическом уровне, основываясь на простых представлениях электронной теории проводимости металлов Друде-Лоренца. Разглядим электрический ток в железных проводниках, снутри которых существует поле с напряженностью Е. Оно действует на свободные электроны проводимости с силой F = ее, где е заряд электрона. Эта сила докладывает электронам с массой m ускорением a = F/m = ee/m. Если б движение электронов в металле происходило без утрат энергии, то их скорость, а поэтому, и сила тока в проводнике с течением времени увеличивались бы. Но при столкновениях с ионами решетки, совершающими хаотичное термическое колебательное движение, электроны теряют часть собственной кинетической энергии. При неизменном токе, когда средняя скорость упорядоченного движения электронов остается с течением времени постоянной, вся энергия, получаемая электронами под действием электрического поля, должна быть передана ионам металла, т. е. должна перейти в энергию их термического движения. Для простоты представим, что при каждом столкновении электрон стопроцентно теряет ту энергию, которую он получил под действием силы F = ее, за время свободного пробега τ от 1-го столкновения до другого. Это значит, что сначала каждого свободного пробега электрон имеет только скорость собственного термического движения, а в конце пробега, перед столкновением, его скорость под действием силы F = ее возрастает до некоторой величины v. Пренебрегая скоростью термического движения, можно считать, что перемещение электрона в направлении деяния силы со стороны поля является равноускоренным с исходной скоростью v 0 = 0. За время свободного пробега электрон приобретает скорость упорядоченного движения a τ eеτ / m, а средняя скорость этого движения v

3 5 v v e 0 v E τ. m Время свободного пробега определяется средней скоростью термического движения электрона u и средней длиной свободного пробега электрона λ: τ = λ/u. Тогда плотность тока в проводнике ne λ j nev E. m u ne λ Величина γ охарактеризовывает характеристики проводника и именуется его удельной электропроводностью. С учетом этого обозначения плот- m u ность тока запишется как j = γe. (5) Это мы получили закон Ома в дифференциальной форме. Учтем сейчас то событие, что на электрон, участвующий в разработке неизменного тока на произвольно избранном участке цепи, должны действовать, не считая кулоновских, к тому же посторонние силы. Тогда (5) воспримет вид j j γ(eкул Естор) либо E Е кул стор. (6) γ Умножим (6) на элемент длины проводника dl и проинтегрируем приобретенное выражение по участку проводника от сечения до сечения: j Е dl Е dl кул стор dl. (7) γ I С учетом того, что для неизменного тока j и γ, где ρ удельное сопротивление проводника, выражение (7) воспримет S ρ вид ρ Екулdl Есторdl I dl. (8) S 1-ый интеграл в (8) представляет собой разность потенциалов (φ φ) между точками сечений и. 2-ой интеграл находится в зависимости от источника сил и именуется электродвижущей силой. Интеграл в правой части (8) охарактеризовывает характеристики проводника и именуется сопротивлением R участка проводника. Если S и ρ постоянны, то

4 6 l R ρ. (9) S Таким макаром, формула (8) имеет вид φ φ ξ IR U. (0) Это обобщенный закон Ома в интегральной форме для неоднородного участка цепи. (U падение напряжений на участке -). В случае однородного участка проводника, т. е. при отсутствии на этом участке посторониих сил, из (0) имеем φ φ IR. () Если цепь замкнута (φ φ), то из (0) получаем ξ IRц I(R внешн rвнутр), () где R ц сопротивление всей цепи, включая наружное R внешн и внутреннее сопротивление источника тока r внутр. ОПИСАНИЕ УСТАНОВКИ И Способа ИЗМЕРЕНИЯ Рис.. Вид установки 6 Установка состоит (рис.) из измерительной части и колонны с метрической шкалой. На колонне смонтированы два недвижных кронштейна, между которыми натянут хромоникелевый провод 3. По колонне перемещается подвижный кронштейн 4, обеспечивающий контакт с проводом. На лицевой панели размещены вольтметр 5, миллиамперметр 6, включатель «сеть», регулятор тока, кнопочный переключатель диапазонов вольтметра 7, который сразу переключает вольтметр с измерения падения напряжения на измерение ЭДС. На рис. приводится схема измерения падения напряжения U и ЭДС источника тока. В цепь источника тока последовательно врубается переменное сопротивление r, выполняющее роль внутреннего сопротивления источника, ручка регулятора которого, «регулятор тока», выведена на лицевую панель устройства. Переменное сопротивление r позволяет регулировать силу тока в цепи источника. Данная схема позволяет моделировать работу источника тока с регули-

5 7 руемым внутренним сопротивлением. Наружной нагрузкой R служит сопротивление однородного проводника, длину которого, а поэтому, и R можно регулировать перемещением подвижного кронштейна. При замкнутом ключе К воз- V никает электрический ток в цепи r rr. Цепь состоит из неоднородного участка r и однород- А φ + φ ного участка R. Согласно обозначенному направлению тока запишем законы Ома для одно- К I R родного и неоднородного участков цепи. Для участка R: φ φ IR. Рис.. Схема измерения U и ε Для участка εr: φ φ ξ Ir. Для замкнутой цепи, содержащей однородный и неоднородный участки, можно записать, сложив эти уравнения (φ φ) (φ φ) ξ I(R r). Получили закон Ома для замкнутой цепи: ξ I(R r). (3) Разность потенциалов φ φ с учетом () и (3) может быть выражена формулой ξr φ φ. R r При размыкании ключа К (R =, а I = 0) φ φ =. Используя закон Ома для замкнутой цепи, можно высчитать сопротивление r для неоднородного участка по формуле ξ U r, U = φ φ. (4) I Мысль работы состоит в проверке закона Ома для замкнутой цепи. С этой целью измеряется падение напряжения U на сопротивлении R однородного цилиндрического проводника при различных величинах силы тока I, протекающего по участку цепи. На основании измерений U и I строится вольт-амперная черта проводника. Величина сопротивления проводника определяется как тангенс угла наклона свойства к оси I. На рис. 3 приводится вольт-амперная черта проводника: ΔU R tgα. (5) ΔI

6 8 Установленная графическая зависимость между величинами U, I, R выражает закон Ома для однородного U участка цепи: α ΔI ΔU I Рис. 3. Вольт-амперная черта проводника Δφ = U = IR. (6) В случае цилиндрического однородного проводника с поперечником d, длиной l и удельным электросопротивлением ρ величина R может быть определена формулой l 4l R ρ ρ. (7) S πd ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Задание I. Исследование вольт-амперной свойства проводника.. Составить таблицу измерений (табл.). Таблица I, ма U, В. Отжать кнопочный переключатель (измерение U). 3. Вывести подвижный кронштейн 4 в среднее положение (l = 5 см). 4. Включить установку в сеть. 5. Регулятором тока установить малое значение силы тока. 6. Записать показания вольтметра и амперметра в табл.. 7. Увеличивая силу тока регулятором, снять зависимость U от I (5 0 значений). 8. Выстроить вольт-амперную характеристику. 9. Вычислить при помощи графика сопротивление проводника по формуле (5). 0. Зная сопротивление проводника R, по формуле (7) найти удельное электросопротивление ρ. Поперечник проводника d = 0,36 мм.. Прийти к выводу.

7 9 Задание II. Исследование воздействия сопротивления участка цепи на величину падения напряжения на участке.. Составить табл. измерений. Таблица l, см U, В. Отжать кнопочный переключатель (измерение U). 3. Установить подвижный кронштейн в положение l = 0 см. 4. Включить установку в сеть. 5. Регулятором тока установить силу тока 50 ма. 6. Записать в табл. показания вольтметра U и l. 7. Увеличивая длину проводника l, снять зависимость U от l, при всем этом регулятором тока поддерживать значение I = 50 ма. 8. Выстроить график зависимости U от l. 9. Прийти к выводу. Задание III. Исследование закона Ома для замкнутой цепи.. Составить табл. 3 измерений. Таблица 3 I, mа U, B R, Ом r, Ом, В I(R + r), B 50. Отжать кнопочный переключатель (измерение U). 3. Установить подвижный кронштейн в положение l = 5 см. 4. Включить установку в сеть. 5. Регулятором тока установить силу тока 50 ма. 6. Записать показания вольтметра U в табл Надавить кнопочный переключатель (измерение ЭДС). При всем этом происходит расширение спектра измерений вольтметра. Стоимость деления вольтметра в схеме измерения ЭДС составляет 0,5 В. Измерить величину ЭДС () и записать в табл Величину сопротивления R взять из результатов измерений задания I. Итог записать в табл Высчитать величину сопротивления r для неоднородного участка цепи по формуле (4). Итог записать в табл. 3.

8 0 0. Проверить закон Ома для замкнутой цепи. Для этого отыскать значение I(R + r); приобретенный итог сопоставить с измеренным значение.. Прийти к выводу. КОНТРОЛЬНЫЕ ВОПРОСЫ. Сформулируйте законы Ома для замкнутой цепи и участка цепи.. Каковой физический смысл ЭДС источника? 3. Как измерить ЭДС источника, включенного в цепь? 4. Почему амперметры имеют маленькое, а вольтметры очень огромное сопротивление? 5. Каким условиям должно удовлетворять заземляющее устройство? Разъяснить. 6. Какими величинами характеризуется электрическое поле? 7. Что такое напряженность электрического поля? 8. Что именуется потенциалом? 9. Нарисуйте схему параллельного и последовательного соединения 2-ух источников неизменного тока. 0. С какой целью включают источники тока последовательно?. С какой целью соединяют источники тока параллельно?. В каких единицах измеряются сила тока, плотность тока, разность потенциалов, напряжение, ЭДС, сопротивление электрическому току, проводимость? 3. Что такое удельное сопротивление? 4. От чего зависит удельное сопротивление железного проводника? 5. Как, зная потенциалы, надлежащие двум примыкающим эквипотенциальным линиям, и расстояние между ними, отыскать напряженность поля? 6. Установите связь между потенциалом и напряженностью поля. 7. Придите к выводу обобщенного закона Ома в интегральной форме из закона Ома в дифференциальной форме. БИБЛИОГРАФИЧЕСКИЙ Перечень. Детлаф А. А, Курс физики: учеб. пособ. для вузов / А. А. Детлаф, Б. М. Яворский М.: Высш. шк., с.. Трофимова Т. И. Курс физики: учеб. пособ. для вузов / Т. И. Трофимова М.: Высш. шк., с. 3. Терентьев Н. Л. Электричество. Электромагнетизм: учеб. пособ. / Н. Л. Терентьев Хабаровск: Изд-во Хабар. гос. техн. ун-та, с.

Столичный Муниципальный ТЕХНИЧЕСКИЙ Институт «МАМИ» Кафедра физики ЛАБОРАТОРНАЯ РАБОТА.04 Исследование ЗАКОНОВ Неизменного ТОКА Москва 00 г. Лабораторная работа.04 Исследование ЗАКОНОВ Неизменного ТОКА Цель

Методические указания к выполнению лабораторной работы.1.7 ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ МЕТАЛЛОВ Аникин А.И., Фролова Л.Н. Электрическое сопротивление металлов: Методические указания к выполнению лабораторной

Определение удельного сопротивления проводника. Введение. Электрическим током именуют упорядоченное движение заряженных частиц. Сами эти частички именуются носителями тока. В металлах и полупроводниках