Сопротивление проводника ограничивает величину тока в электрической цепи. Чем больше величина сопротивление, тем меньше ток. Расчет сопротивления проводника можно произвести 2-мя методами: 1-ый метод заключается в использовании формулы закона Ома, а 2-ой вариант расчета предполагает познание геометрических размеров проводника и удельного сопротивления вещества, из которого он изготовлен.
Почему проводник “сопротивляется”?
Напряжение U, поданное на концы проводника, делает снутри него электрическое поле, которое приводит в движение свободные электроны вещества. Электроны, получив дополнительную кинетическую энергию, начинают двигаться упорядоченно в одном направлении, создавая тем электрический ток цепи.
В процессе движения электроны сталкиваются с нейтральными и заряженными атомами, из которых стоит проводник, теряют энергию. Масса атома превосходит массу электрона в тысячи раз, потому их столкновение приводит к изменению направления движения электронов и потере скорости (“торможению”).
Таким макаром появляется сопротивление протеканию (нарастанию) тока.
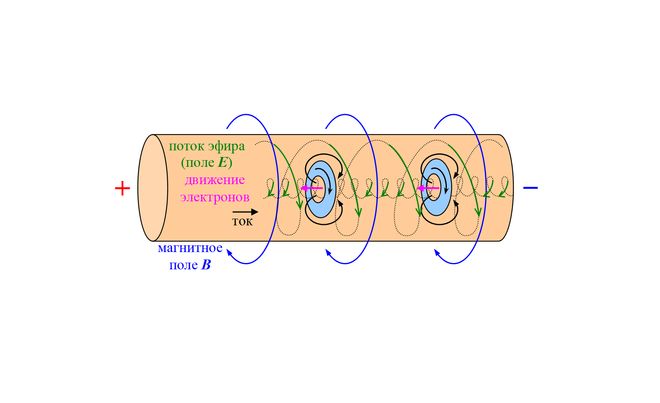
Рис. 1. Электрический ток в проводнике ограничивается столкновением электронов с атомами.
Расчет сопротивления при помощи закона Ома
Германский физик Георг Ом в 1826 г. нашел, что отношение напряжения U между концами железного проводника, являющегося участком электрической цепи, к силе тока I есть величина неизменная:
Данную величину стали именовать электрическим сопротивлением. Пользуясь этой формулой, можно экспериментально найти величину неведомого сопротивления.
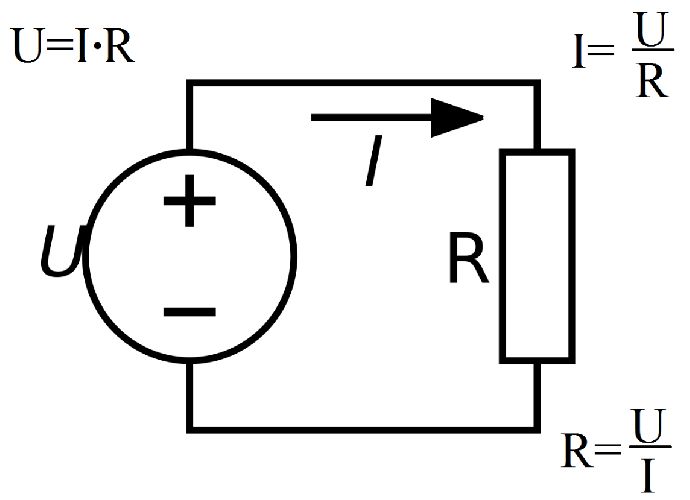
Рис. 2. Схема измерения напряжения и тока для определения сопротивления участка цепи.
Для этого амперметром измеряется величина электрического тока через сопротивление, а вольтметром — напряжение на участке цепи. Дальше, применяя формулу (1), рассчитывается значение R.
Единица измерения названа в честь Георга Ома. Электрическим сопротивлением 1 Ом обладает участок цепи, на котором при силе тока 1 А напряжение равно 1 В:
Расчет при помощи удельного сопротивления
Расчет сопротивления проводника можно произвести без измерения величин напряжения и тока. Но для этого следует знать дополнительную информацию о проводнике.
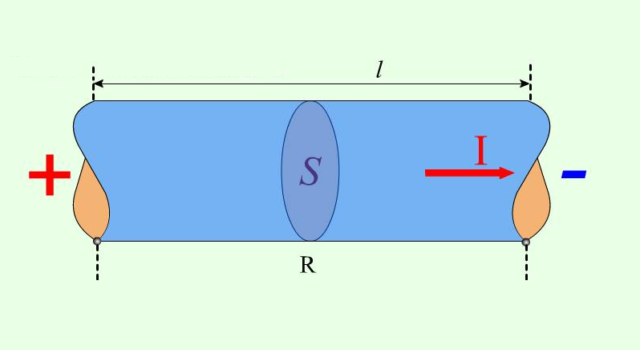
Рис. 3. Проводник с поперечным сечением S и длиной L, через который течет ток I.
Георг Ом и другие исследователи опытным методом обусловили, что сопротивление проводника прямо пропорционально длине проводника L и назад пропорционально площади поперечного сечения проводника S. Эту закономерность можно обрисовать формулой расчета сопротивления проводника:
Коэффициент ρ был назван удельным сопротивлением. Эта физическая величина отражает особенности определенного вещества, которые зависят от плотности вещества, кристаллической структуры, строения атомов и других внутренних характеристик. Расчет удельного сопротивления проводника создавать всякий раз необязательно, так как для большинства веществ удельные сопротивления измерены и сведены в справочные таблицы, которые можно отыскать в картонных справочниках либо в их интернет-версиях.
Но если такая необходимость возникнет, то из формулы (2) можно получить следующую формулу (3), и по ней высчитать ρ:
Серебро имеет одно из самых низких значений ρ, равное $ 0,016 <Ом*мм^2\over м>$. Этим разъясняется внедрение такового достаточно дорогого металла для пайки в особенности принципиальных радиодеталей (микросхем, процессоров, электронных плат), которые должны как можно меньше греться в процессе работы.
Что мы узнали?
Итак, мы узнали, что расчет сопротивления проводника можно произвести 2-мя методами. 1-ый расчет проводится при помощи формулы закона Ома после измерения величин напряжения и тока. Для второго расчета нужна информация о геометрических размерах проводника и его удельном сопротивлении.
Полное сопротивление цепи переменного тока
В прошлых статьях мы узнали, что всякое сопротивление, поглощающее энергию, именуется активным, а сопротивление, не поглощающее энергии, безваттным либо реактивным. Не считая того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.
Но есть цепи, где сопротивление не является чисто активным либо чисто реактивным. Другими словами цепи, где совместно с активным сопротивлением включены в цепь, как емкости, так и индуктивности.
Введем понятие полного сопротивления цепи переменному току — Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам нужно для более полного осознания закона Ома для переменного тока
На рисунке 1 представлены варианты электрических цепей и их систематизация зависимо от того какие элементы (активные либо реактивные) включены в цепь.
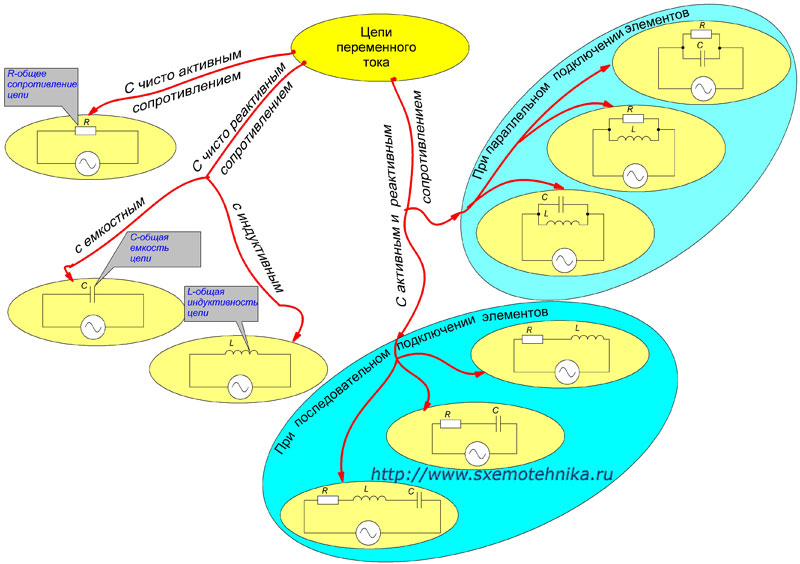
Набросок 1. Систематизация цепей переменного тока.
Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами гласили, и оно зависит соответственно от общей емкости и индуктивности цепи.
Разглядим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.
Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.
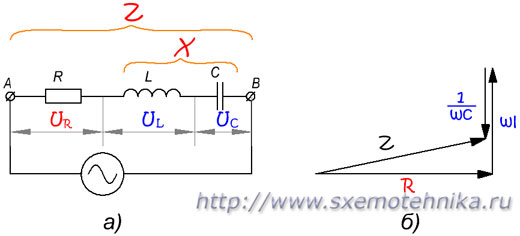
В любом сечении цепи, изображенной на рисунке 2,а, секундные значения тока должны быть одинаковыми, так как в неприятном случае наблюдались бы скопления и разрежения электронов в каких-то точках цепи. Другими словами, фазы тока по всей длине цепи должны быть одинаковыми. Не считая того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (набросок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) смещены друг относительно друга на угол в 90°.
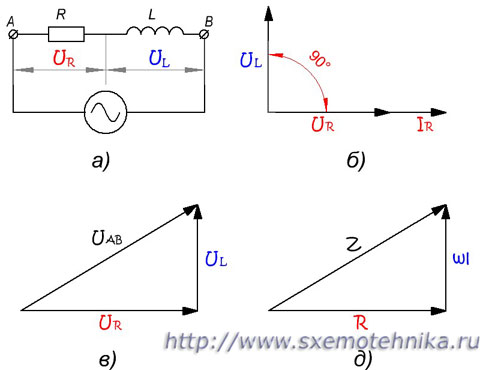
Набросок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) — схема цепи; б) — сдвиг фаз тока и напряжения; в) — треугольник напряжений; д) — треугольник сопротивлений.
Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника.
Из геометрии понятно, что квадрат гипотенузы равен сумме квадратов катетов.
По закону Ома напряжение должно приравниваться силе тока, умноженной на сопротивление.
Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z 2 ) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.
(1)
Извлекая квадратный корень из обеих частей этого равенства, получим,
(2)
Таким макаром, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений
Полное сопротивление можно отыскивать не только лишь методом вычисления, но и методом построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено методом измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Очевидно, измерения катетов и гипотенузы должны выполняться в одном и том же масштабе. Так, к примеру, если мы договорились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу см, укладывающихся на гипотенузе.
Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит внутри себя оба эти вида сопротивлений. Потому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, другими словами он будет больше 0°, но меньше 90°. К которому из этих 2-ух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и напротив, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.
В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление таковой цепи можно найти с помощью треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.
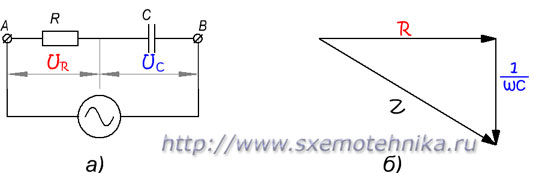
Набросок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) — схема цепи; б) — треугольник сопротивлений .
Разница между обоими вариантами состоит только в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.
Для данного варианта:
(3)
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), поначалу определяется реактивное сопротивление этой цепи, а потом уже полное сопротивление цепи.
Набросок 4. Полное сопротивление цепи содержащей R, L и C. а) — схема цепи; б) — треугольник сопротивлений .
Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления обратны друг дружке по собственному нраву, то общее реактивное сопротивление цепи будет равно их разности, т. е.
(4)
Общее реактивное сопротивление цепи может иметь индуктивный либо емкостный нрав, зависимо от того, какое из этих 2-ух сопротивлений (XL либо XC преобладает).
После того как мы по формуле (4) обусловили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.
(5)
(6)
Метод построения треугольника сопротивлений для этого варианта изображен на рис. 4 б.
Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того дабы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), необходимо поначалу вычислить проводимость каждой из параллельных веток, позже найти полную проводимость всей цепи между точками А и В и потом вычислить полное сопротивление цепи между этими точками.
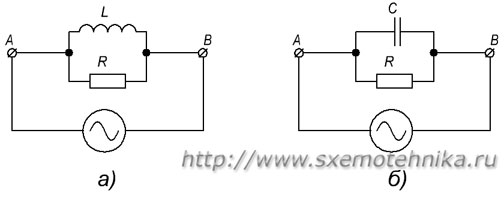
Набросок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных частей. а) — параллельное соединение R и L; б) — параллельное соединение R и C .
Проводимость активной ветки, как понятно, равна 1/R, аналогично проводимость индуктивной ветки равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.
(7)
Приводя к общему знаменателю подкоренное выражение, получим:

(8)
(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
Нахождение полного сопротивления для этого варианта может быть произведено и геометрическим методом. Для этого необходимо выстроить в соответственном масштабе треугольник сопротивлений, и потом произведение длин катетов поделить на длину гипотенузы. Приобретенный итог и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:
(10)
Полное сопротивление может быть найдено также и в данном случае методом построения треугольника сопротивлений.
В радиотехнике более нередко встречается случай па¬раллельного соединения индуктивности и емкости, к примеру колебательный контур для опции приемников и передатчиков. Так как катушка индуктивности всегда обладает не считая индуктивного к тому же активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветки активное сопротивление (рис 7).
Набросок 6. Эквивалентная схема колебательного контура.
Формула полного сопротивления для этого варианта будет:
(11)
Так как обычно активное сопротивление катушки (R) бывает сильно мало по сопоставлению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:

(12)
В колебательном контуре обычно подбирают величины L и С таким макаром, дабы индуктивное сопротивление приравнивалось емкостному, т. е. дабы соблюдалось условие
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:
(14)
где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
Приглянулась СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В Соц СЕТЯХ!