В механической системе обязанные колебания появляются при действии на нее наружной повторяющейся силы. Аналогично этому обязанные электромагнитные колебания в электрической цепи происходят под действием наружной временами изменяющейся ЭДС либо наружного изменяющегося напряжения.
Обязанные электромагнитные колебания в электрической цепи представляют собой переменный электрический ток.
- Переменный электрический ток — это ток, сила и направление которого временами изменяются.
Мы в предстоящем будем учить обязанные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω по синусоидальному либо косинусоидальному закону:
\(~u = U_m \cdot \sin \omega t\) либо \(~u = U_m \cdot \cos \omega t\) ,
где u – секундное значение напряжения, Um – амплитуда напряжения, ω – повторяющаяся частота колебаний. Если напряжение изменяется с частотой ω, то и сила тока в цепи будет изменяться с той же частотой, но колебания силы тока не непременно должны совпадать по фазе с колебаниями напряжения. Потому в общем случае
\(~i = I_m \cdot \sin (\omega t + \varphi_c)\) ,
где φc – разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Исходя из этого можно дать еще такое определение:
- Переменный ток – это электрический ток, который меняется со временем по гармоническому закону.
Переменный ток обеспечивает работу электрических движков в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это значит, что в протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока в почти всех странах мира. В США частота промышленного тока 60 Гц.
Генератор переменного тока
Основная часть электроэнергии в мире в текущее время вырабатывается генераторами переменного тока, создающими гармонические колебания.
- Генератором переменного тока именуется электротехническое устройство, созданное для преобразования механической энергии в энергию переменного тока.
ЭДС индукции генератора меняется по синусоидальному закону
\(e=_ \cdot \sin \omega \cdot t,\)
где \(_ =B\cdot S\cdot \omega\) — амплитудное (наибольшее) значение ЭДС. При подключении к выводам рамки нагрузки сопротивлением R, через нее будет перейти переменный ток. По закону Ома для участка цепи сила тока в нагрузке
\(i=\dfrac =\dfrac \cdot \sin \omega \cdot t = I_ \cdot \sin \omega \cdot t,\)
где \(I_ = \dfrac\) — амплитудное значение силы тока.
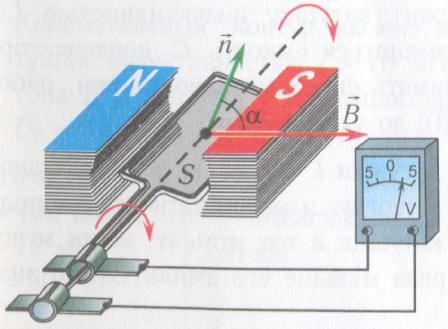
Основными частями генератора являются (рис. 1):
- индуктор — электромагнит либо неизменный магнит, который делает магнитное поле;
- якорь — обмотка, в какой индуцируется переменная ЭДС;
- коллектор со щетками — устройство, средством которого снимается с крутящихся частей либо подается по ним ток.
Недвижная часть генератора именуется статором, а подвижная — ротором. Зависимо от конструкции генератора его якорь может быть как ротором, так и статором. При получении переменных токов большой мощности якорь обычно делают недвижным, дабы упростить схему передачи тока в промышленную сеть.
На современных гидроэлектростанциях вода крутит вал электрогенератора с частотой 1-2 оборота за секунду. Таким макаром, если б якорь генератора имел только одну рамку (обмотку), то выходил бы переменный ток частотой 1-2 Гц. Потому, для получения переменного тока промышленной частоты 50 Гц якорь должен содержать несколько обмоток, позволяющих прирастить частоту вырабатываемого тока. Для паровых турбин, ротор которых крутится очень стремительно, применяют якорь с одной обмоткой. В данном случае частота вращения ротора совпадает с частотой переменного тока, т.е. ротор должен делать 50 об/с.
Массивные генераторы вырабатывают напряжение 15-20 кВ и владеют КПД 97-98 %.
Из истории. Сначало Фарадей нашел только чуть приметный ток в катушке при движении поблизости нее магнита. «Какая от этого полезность?» — спросили его. Фарадей ответил: «Какая может быть полезность от новорожденного?» Прошло немногим больше половины столетия и, как произнес американский физик Р. Фейнман, «бесполезный новорожденный перевоплотился в чудо-богатыря и изменил вид Земли так, как его гордый отец не мог для себя и представить».
*Принцип деяния
Принцип деяния генератора переменного тока основан на явлении электромагнитной индукции.
Пусть проводящая рамка площадью S крутится с угловой скоростью ω вокруг оси, расположенной в ее плоскости перпендикулярно однородному магнитному полю индукцией \(\vec\) (см. рис. 1).
При равномерном вращении рамки угол α между направлениями вектора индукции магнитного поля \(\vec\) и нормали к плоскости рамки \(\vec\) изменяется с течением времени по линейному закону. Если в момент времени t = 0 угол α0 = 0 (см. рис. 1), то
\(\alpha = \omega \cdot t = 2\pi \cdot \nu \cdot t,\)
где ω — угловая скорость вращения рамки, ν — частота ее вращения.
В данном случае магнитный поток, пронизывающий рамку будет изменяться следующим образом
\(\Phi \left(t\right)=B\cdot S\cdot \cos \alpha =B\cdot S\cdot \cos \omega \cdot t.\)
Тогда согласно закону Фарадея индуцируется ЭДС индукции
\(e=-\Phi ‘(t)=B\cdot S\cdot \omega \cdot \sin \omega \cdot t = _ \cdot \sin \omega \cdot t.\)
Подчеркнем, что ток в цепи проходит в одном направлении в течение полуоборота рамки, а потом меняет направление на обратное, которое также остается постоянным в течение следующего полуоборота.
Действующие значения силы тока и напряжения
Пусть источник тока делает переменное гармоническое напряжение
\(u=U_ \cdot \sin \omega \cdot t.\;\;\;(1)\)
Согласно закону Ома, сила тока в участке цепи, содержащей только резистор сопротивлением R, присоединенный к этому источнику, меняется с течением времени также по синусоидальному закону:
\(i = \dfrac =\dfrac > \cdot \sin \omega \cdot t = I_ \cdot \sin \omega \cdot t,\;\;\; (2)\)
где \(I_m = \dfrac>.\) Как лицезреем, сила тока в таковой цепи также изменяется со временем по синусоидальному закону. Величины Um, Im именуются амплитудными значениями напряжения и силы тока. Зависящие от времени значения напряжения u и силы тока i именуют моментальными.
Не считая этих величин применяются еще одна черта переменного тока: действующие (действенные) значения силы тока и напряжения.
- Действующим (действенным) значением силы переменного тока именуется сила такового неизменного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Обозначается буковкой I.
- Действующим (действенным) значением напряжения переменного тока именуется напряжение такового неизменного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Обозначается буковкой U.
Действующие (I, U) и амплитудные (Im, Um) значения связаны между собой следующими соотношениями:
\(I = \dfrac >, \; \; \; U =\dfrac >>.\)
Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:
\(P = U\cdot I = I^ <2>\cdot R = \dfrac>.\)
Стоит отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R, осуществляется как для амплитудных и действующих, так и для моментальных значений напряжения и силы тока, вследствие того, что их колебания совпадают по фазе.
*Вывод формулы
Зная секундные значения u и i, можно вычислить секундную мощность
которая, в отличие от цепей неизменного тока, меняется со временем. С учетом уравнений (1) и (2) перепишем выражение для моментальной мощности на резисторе в виде
\(p=U_ \cdot I_ \cdot \sin ^ \omega \cdot t=U_ \cdot I_ \cdot \dfrac =\dfrac \cdot I_ > -\dfrac \cdot I_ > \cdot \cos 2\omega \cdot t.\)
1-ое слагаемое не находится в зависимости от времени. 2-ое слагаемое P2 — функция косинуса двойного угла и ее среднее значение за период колебаний равно нулю (рис. 2, найдите сумму площади выделенных фигур с учетом символов).
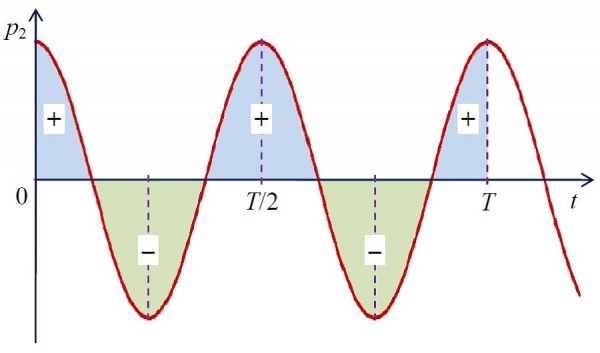
Потому среднее значение мощности переменного электрического тока за период будет равно
\(\left\langle P \right\rangle =\dfrac .\)
Тогда с учетом закона Ома \(\left(I_ =\dfrac \right)\) получаем:
\(\left\langle P \right\rangle = \dfrac \cdot R=\dfrac^ >. (4)\)
По определению действующих значений необходимо сравнивать мощности (количество теплоты в единицу времени) переменного и постоянного тока. Запишем уравнения для расчета мощности постоянного тока
и сравним с уравнениями (4>:
\(\dfrac \cdot R = I^ \cdot R, \;\;\; I=\dfrac<\sqrt>,\)