Форму закона ома для участка цепи

В 1827 г. германский физик Г. Ом, проведя серию четких тестов, установил один из главных законов электрического тока. Он говорит: постоян­ный электрический ток в участке электрической цепи прямо пропорциона­лен напряжению на этом участке.

Закон Ома имеет разные формы записи.

В дифференциальной форме для участка цепи без ЭДС он имеет вид

, (1.2)

где – удельная проводимость.

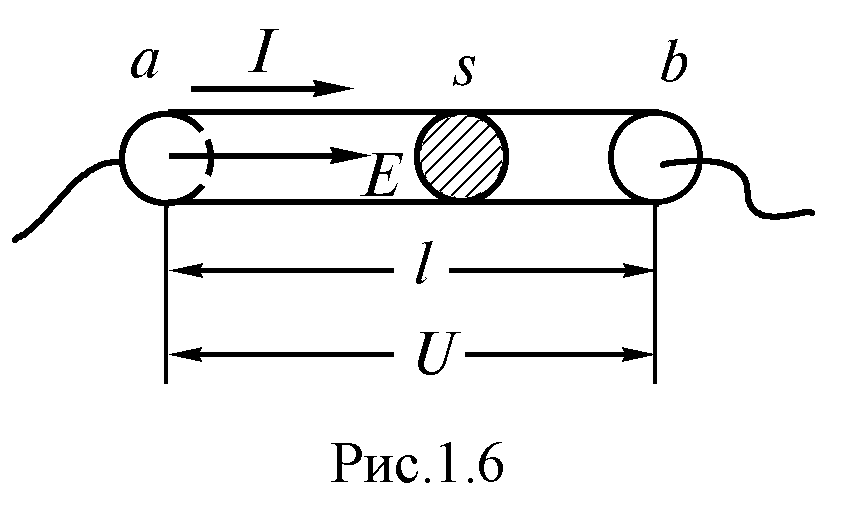
Разглядим прямолинейный проводник неизменного сечения s (рис. 1.6):

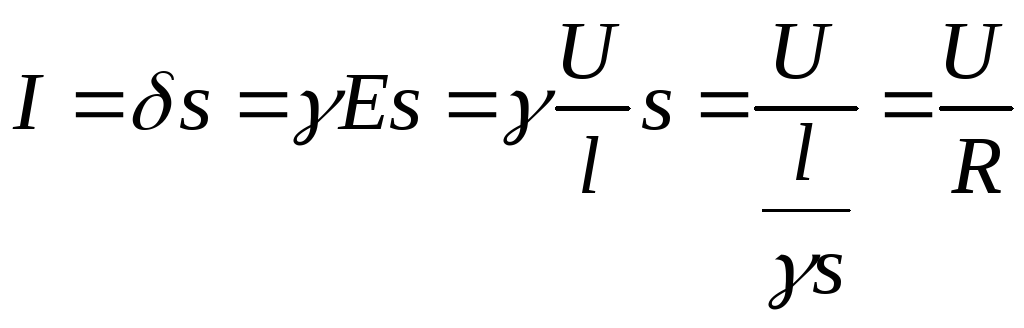
. (1.3)

Это 2-ая форма записи закона Ома для участка цепи без ЭДС, которая назы­вается интегральной. Он формулируется следующим образом: ток в провод­нике равен отношению падения напряжения на участке проводника к элек­трическому сопротивлению участка.

Электрическое сопротивлениепрямо пропорционально длинеи об­ратно пропорционально площади поперечного сечения проводника:

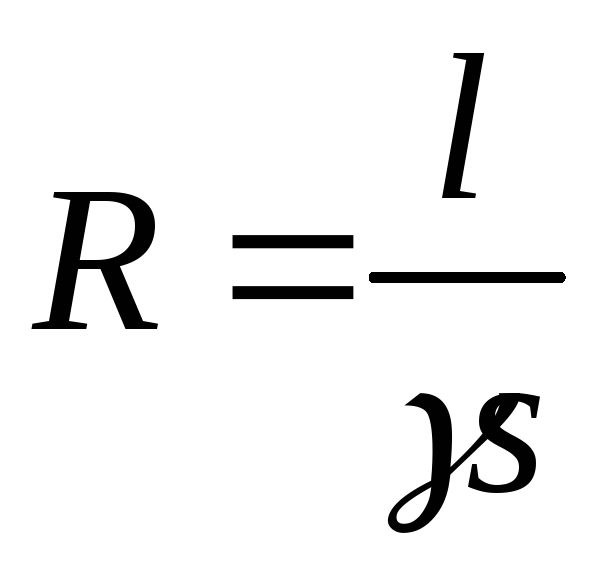
. (1.4)

Размерность сопротивления.

Таким макаром, сопротивление– это скалярная величина, характеризую­щая проводящие характеристики цепи. Оно равно отношению неизменного напряжения на участке цепи к току в нем при отсутствии на участке ЭДС:

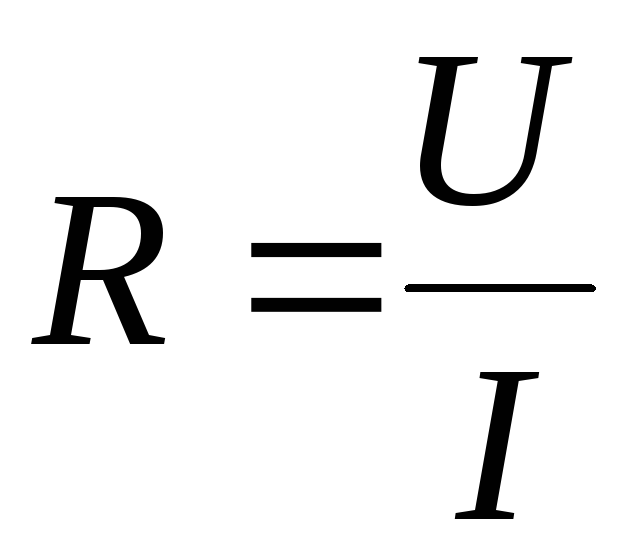
. (1.5)

Сопротивление – это величина, показывающая, что в данном участке цепи происходит преобразование энергии.

Величина, оборотная сопротивлению, именуется проводимостью:

. (1.6)

Размерность проводимости – сименс (См). 1 См = 1/Ом.

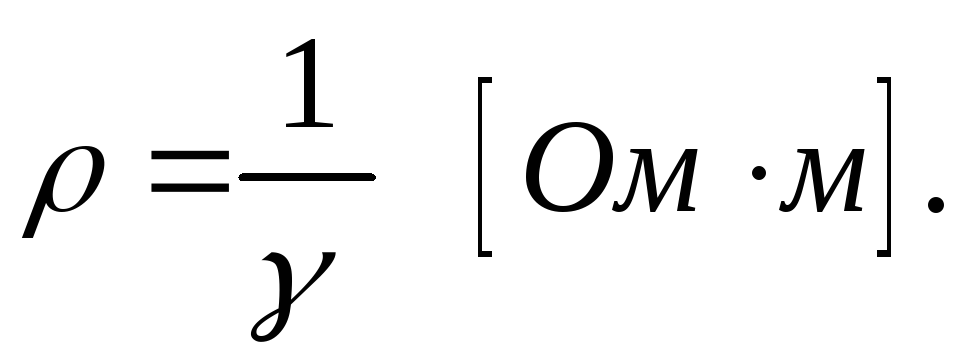
(1.7)

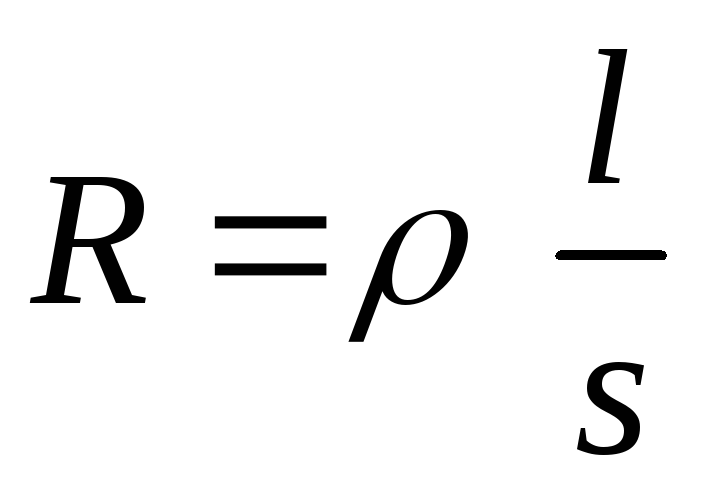
. (1.8)

Удельное сопротивление получено экспериментально для всех материалов и приведено в справочниках.

Обмотки реостатов и нагревательных устройств изготавливают из сплавов с огромным удельным сопротивлением (нихром, фехраль и т.п.).

Устройства, которые включают в электрическую цепь для ограничения либо регулирования тока, именуются резисторами либо реостатами.

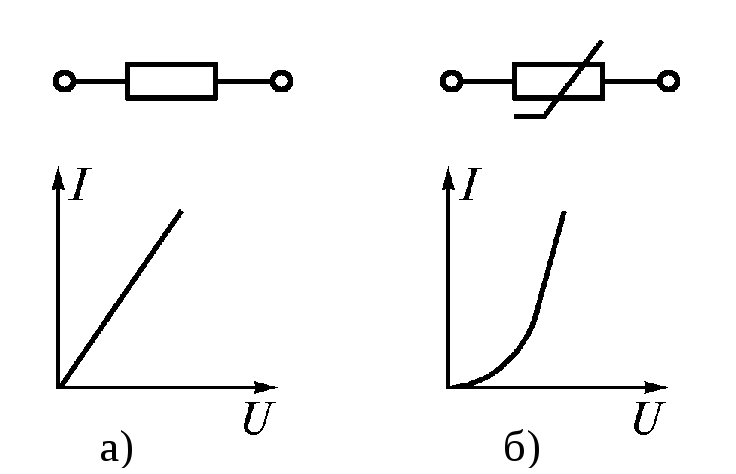
Зависимость тока резистораIот подво­димого напряженияUименуется еговольт­амперной чертой(ВАХ). Если сопротивление резистора не находится в зависимости от тока, то его ВАХ представляет собой прямую линию (рис. 1.7 а), проходящую через начало координат. Таковой резистор именуетсялинейным. Рези­стор, ВАХ которого не является прямой ли­нией (рис. 1.7 б), именуетсянелинейным. Электрические цепи, содержащие только ли­нейные элементы, именуют линейными. Если в цепи имеется хотя бы один нелинейный элемент, вся цепь именуетсянелиней­ной.

1.4. Источник эдс и источник тока

При преобразовании любого вида энергии в электрическую энергию в источ­никах происходит за счет электродвижущей силы (ЭДС). Электродвижу­щая сила охарактеризовывает действие посторониих (неэлектрических) сил в источни­ках постоян­ного либо переменного тока. В замкнутом проводящем кон­туре она равна работе этих сил по перемещению единичного положительного за­ряда вдоль этого кон­тура. Посторонние силы приводят в движение заряженные частички снутри источ­ника электроэнергии: генераторов, гальванических частей и т.д. ЭДС определяется как отношение работы , совершаемой сто­ронними силами при переносе заряженной частички снутри источника, к ее за­ряду:

.

Если = 1Кл, то.

Поэтому, ЭДС равна работе, совершаемой посторонними силами при переносе единицы заряда снутри источника от зажима с наименьшим потенциалом к зажиму с огромным потенциалом. Ее можно представить разностью потенциалов либо напряжением между положительным и отрицательным зажимами источника энергии при отсутствии в нем тока.

В замкнутой электрической цепи под действием ЭДС источника появляется ток. Цепь, в какой ток не меняется во времени, именуют цепью неизменного тока. При расчете и анализе электрических цепей источник электроэнергии представляют или источником ЭДС, или источником тока.

Безупречным источником ЭДС (рис. 1.8) именуют таковой источник энергии, ЭДС которого не находится в зависимости от протекающего через него тока и равна ЭДС реального источника, а его внутреннее сопротивление равно нулю. На рис. 1.8 показаны ус­ловные обозначения и вольтамперная черта безупречного источника ЭДС.

За положительное направление ЭДС источника принимается направление возрастания потенциала снутри этого источника. Внутреннее сопротивление указывает, что часть энергии, вырабатываемой источником, применяется снутри источника. Схема замещения реального источника (0) может быть представлена в виде последовательного соединения безупречного источника ЭДС и внутреннего сопротивления (рис. 1.9). Реальный источник именуют источни­ком напряжения.

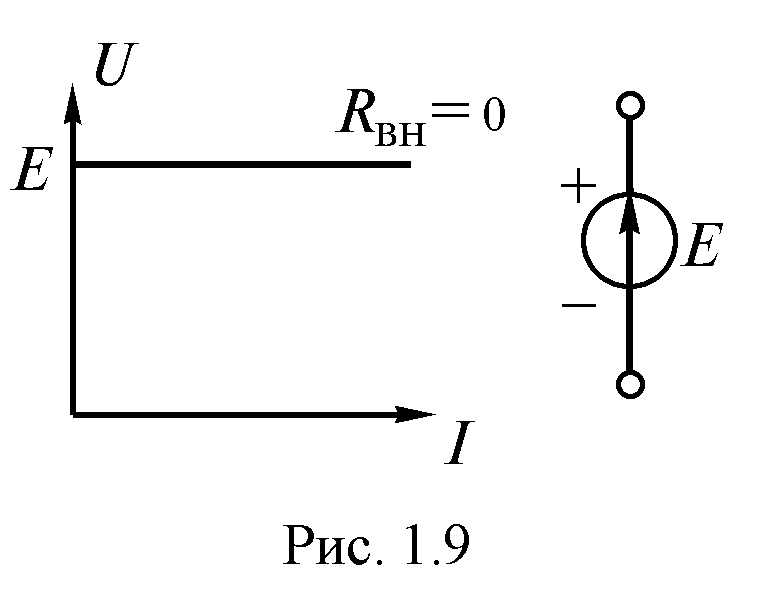
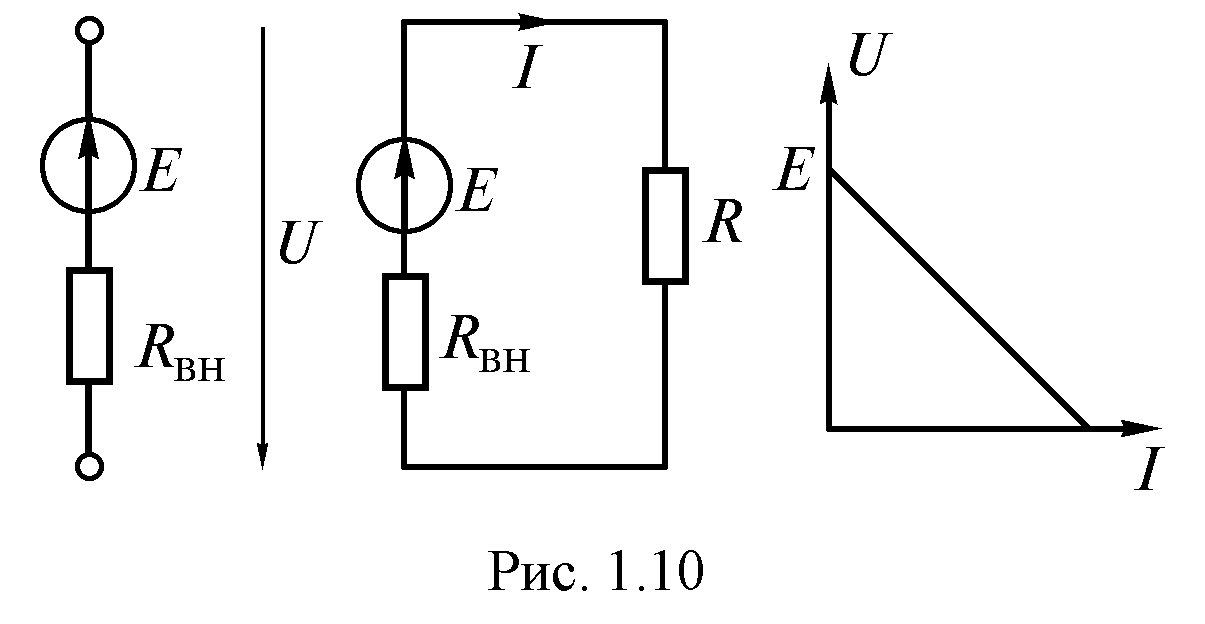
Ток в цепи (рис. 1.9) определяется по закону Ома:

. (1.9)

Из последней формулы видно, что внутреннее сопротивление влияет на ток в электрической цепи.

Напряжение на зажимах источника либо на нагрузке (рис. 1.9) определяется по формуле

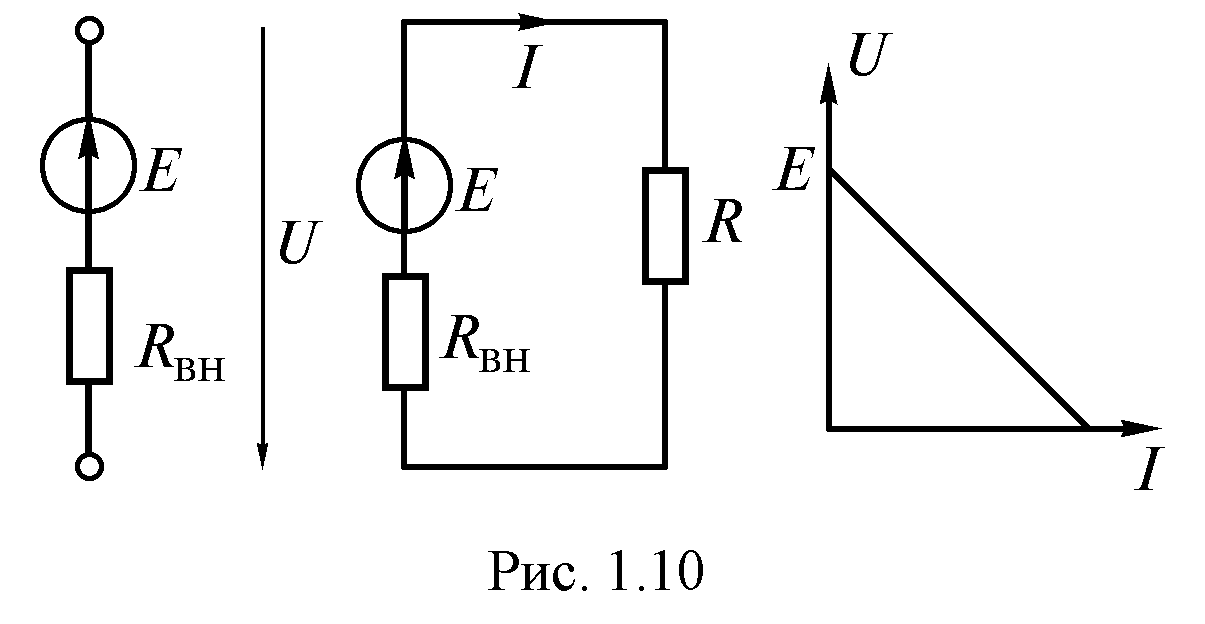
. (1.10)

ВАХ источников электроэнергии нередко именуют наружными чертами. Наружняя черта реального источника описывается уравнением (1.10). Ее можно по­строить по данным 2-ух опытов (рис. 1.10):

холостого хода ;

недлинного замыкания.

Источником токаименуют таковой идеализированный источник электриче­ской энергии, который производит ток, не зависящий от нагрузкицепи и равный личному от деления ЭДС реального источника на его внутрен­нее сопротивление:

. (1.11)

Дабы обеспечить всепостоянство тока независимо от нагрузки, необхо­димо выполнить условия: а); б).

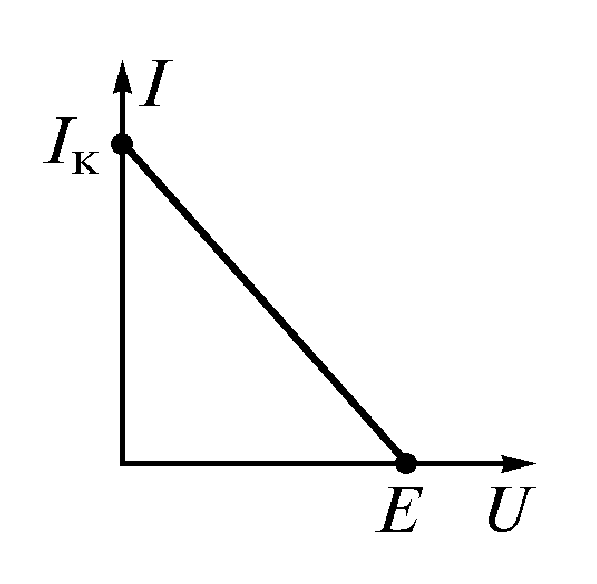
Безупречный источник тока можно считать реальным, если внутреннее сопро­тивление подключить параллельно сопротивлению нагрузки. ВАХ и условное обозначение источника тока показаны на рис. 1.11. Схема замещения реального источника представлена на рис. 1.12.

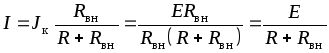
. (1.12)

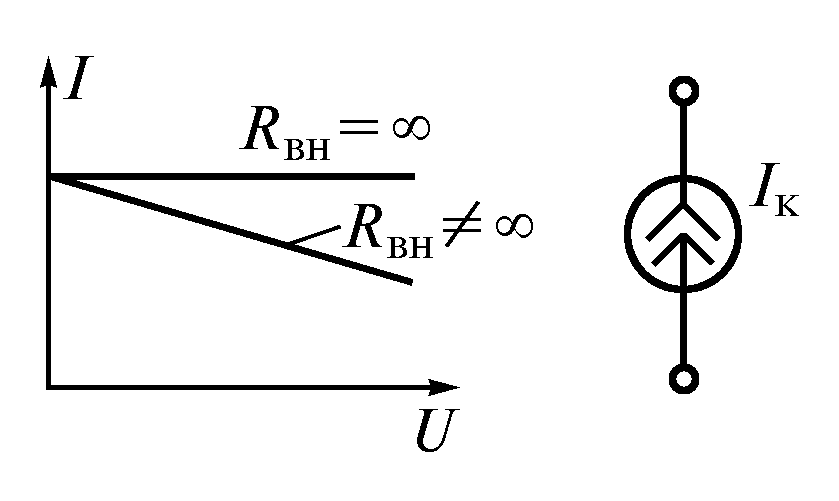
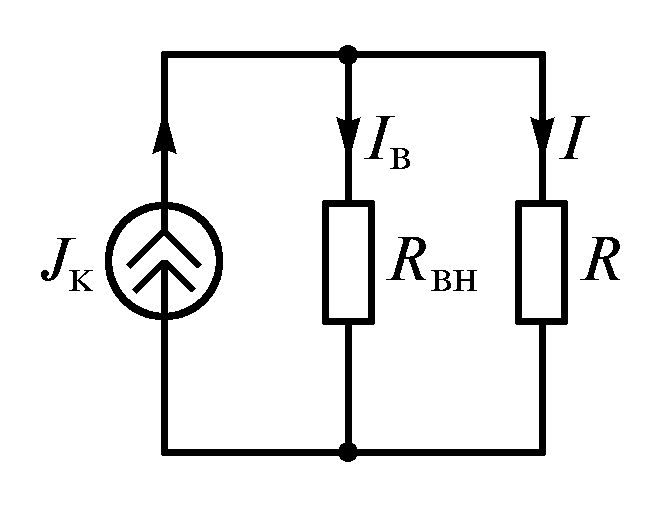
Поэтому, при расчете цепей источники тока могут быть изменены источниками ЭДС и напротив.

Любой из 2-ух расчетных эквивалентов является равноценным. В дальней­шем будем применять в главном источник ЭДС.

Эквивалентность источников обеспечивается при равенстве напряжений при холостом ходе и равенстве токов при маленьком замыкании.

Здесь вы сможете бросить комментарий к избранному абзацу либо сказать об ошибке.

Закон Ома для участка цепи

Июль 17th, 2012 Рубрика: Электротехника

Здрасти, почетаемые читатели веб-сайта «Заметки электрика»..

Сейчас открываю новый раздел на веб-сайте под заглавием электротехника.

В этом разделе я постараюсь в приятной и обычной форме разъяснить Для вас вопросы электротехники. Скажу сходу, что далековато углубляться в теоретические познания мы не будем, но вот с основами познакомимся в достаточном порядке.

1-ое, с чем я желаю Вас познакомить, это с законом Ома для участка цепи. Это самый основной закон, который должен знать каждый электрик.

Познание этого закона дозволит нам беспрепятственно и безошибочно определять значения силы тока, напряжения (разности потенциалов) и сопротивления на участке цепи.

Кто таковой Ом? Мало истории

Закон Ома открыл всем узнаваемый германский физик Георг Симон Ом в 1826 году. Вот так он смотрелся.

Всю биографию Георга Ома я говорить Для вас не буду. Про это Вы сможете выяснить на других ресурсах более тщательно.

Его именованием назван самый основной закон электротехники, который мы интенсивно применяем в сложных расчетах при проектировании, на производстве и в быту.

Закон Ома для однородного участка цепи смотрится следующим образом:

I – значение тока, идущего через участок цепи (измеряется в амперах)

U – значение напряжения на участке цепи (измеряется в вольтах)

R – значение сопротивления участка цепи (измеряется в Омах)

Если формулу разъяснить словами, то получится, что сила тока пропорциональная напряжению и назад пропорциональна сопротивлению участка цепи.

Проведем опыт

Дабы осознать формулу не словестно, а на самом деле, нужно собрать следующую схему:

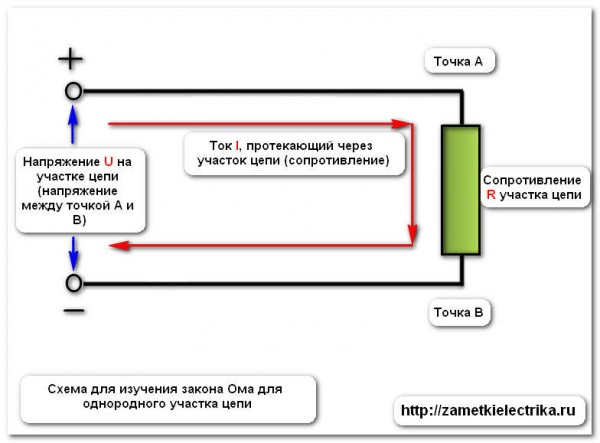
Цель этой статьи — это показать наглядно, как применять закон Ома для участка цепи. Потому я на собственном рабочем щите собрал эту схему. Смотрите ниже как она смотрится.

Сопротивление в цепи я поменял светодиодной лампочкой, обладающей определенной величиной сопротивления. Все соединения производим при помощи соединительных проводов марки ПВ-1. Кто не знает как это выполнить, то читайте мою статью как верно соединять провода.

При помощи ключа управления (избирания) можно избрать, или неизменное напряжение, или переменное напряжение на выходе. В нашем случае применяется неизменное напряжения. Уровень напряжения я меняю при помощи лабораторного автотрансформатора (ЛАТР).

В нашем опыте я буду применять напряжение на участке цепи, равное 220 (В). Контроль напряжения на выходе смотрим по вольтметру.

Сейчас мы стопроцентно готовы провести без помощи других опыт и проверить закон Ома в реальности.

Ниже я приведу 3 примера. В каждом примере мы будем определять разыскиваемую величину 2 способами: при помощи формулы и практическим методом.

Пример № 1

В первом примере нам необходимо отыскать ток (I) в цепи, зная величину источника неизменного напряжения и величину сопротивления светодиодной лампочки.

Напряжение источника неизменного напряжения составляет U = 220 (В). Сопротивление светодиодной лампочки равно R = 40740 (Ом).

При помощи формулы найдем ток в цепи:

I = U/R = 220 / 40740 = 0,0054 (А)

А сейчас проверим приобретенный итог практическим методом.

Подключаем последовательно светодиодной лампочке мультиметр, включенный в режиме амперметр, и замеряем ток в цепи.

На экране мультиметра показан ток цепи. Его значение равно 5,4 (мА) либо 0,0054 (А), что соответствует току, отысканному по формуле.

Пример № 2

Во 2-м примере нам необходимо отыскать напряжение (U) участка цепи, зная величину тока в цепи и величину сопротивления светодиодной лампочки.

I = 0,0054 (А)

R = 40740 (Ом)

При помощи формулы найдем напряжение участка цепи:

U = I*R = 0,0054 *40740 = 219,9 (В) = 220 (В)

А сейчас проверим приобретенный итог практическим методом.

Подключаем параллельно светодиодной лампочке мультиметр, включенный в режиме вольтметр, и замеряем напряжение.

На экране мультиметра показана величина измеренного напряжения. Его значение равно 220 (В), что соответствует напряжению, отысканному по формуле закона Ома для участка цепи.

Пример № 3

В 3-ем примере нам необходимо отыскать сопротивление (R) участка цепи, зная величину тока в цепи и величину напряжения участка цепи.

I = 0,0054 (А)

U = 220 (В)

Снова таки, воспользуемся формулой и найдем сопротивление участка цепи:

R = U/I = 220/0,0054 = 40740,7 (Ом)

А сейчас проверим приобретенный итог практическим методом.

Сопротивление светодиодной лампочки мы измеряем при помощи электроизмерительных клещей либо мультиметра.

Приобретенное значение составило R = 40740 (Ом), что соответствует сопротивлению, отысканному по формуле.

Как просто уяснить Закон Ома для участка цепи.

Дабы не путаться и просто уяснить формулу, можно пользоваться маленький подсказкой, которую Вы сможете выполнить без помощи других.

Нарисуйте треугольник и вчеркните в него характеристики электрической цепи, согласно рисунка ниже. У Вас должно получится вот так.

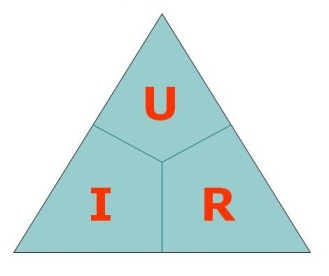
Воспользоваться треугольником-подсказкой совсем не сложно и просто. Закрываете своим пальцем, тот параметр цепи, который нужно отыскать.

Если оставшиеся на треугольнике характеристики размещены на этом же уровне, то означает их нужно перемножить.

Если же оставшиеся на треугольнике характеристики размещены на разном уровне, то тогда нужно поделить верхний параметр на нижний.

При помощи треугольника-подсказки Вы не будете путаться в формуле. Но лучше все же ее выучить, как таблицу умножения.

Выводы

В окончании статьи сделаю вывод.

Электрический ток — это направленный поток электронов от точки В с потенциалом минус к точке А с потенциалом плюс. И чем выше разность потенциалов между этими точками, тем больше электронов переместится из точки В в точку А, т.е. ток в цепи возрастет, при условии, что сопротивление цепи останется прежним.

Но сопротивление лампочки противодействует протеканию электрического тока. И чем больше сопротивление в цепи (последовательное соединение нескольких лампочек), тем меньше будет ток в цепи, при постоянном напряжении сети.

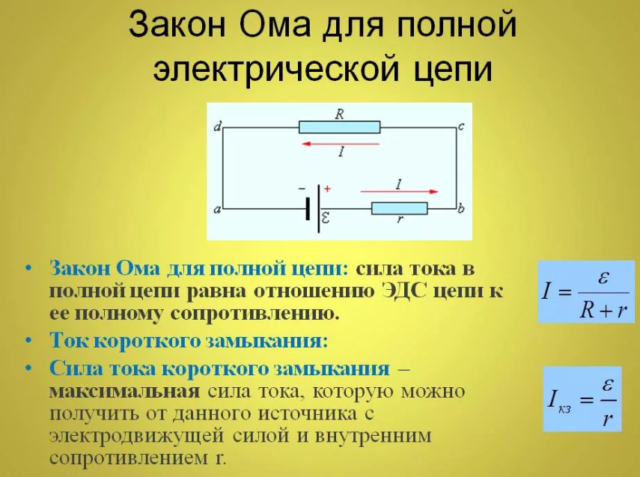
Закон Ома для участка цепи, формула. Закон Ома в дифференциальной форме для полной цепи и её участка

Физический закон ома получен путём тестов. 3 формулировки ома – одни из основополагающих в физике, устанавливающие связь между электротоком, сопротивлением и энергонапряжением. Год открытия – 1826. В первый раз все 3 физических закона ома определил физик-экспериментатор германского происхождения Георг Ом, с фамилией которого связано их определение.

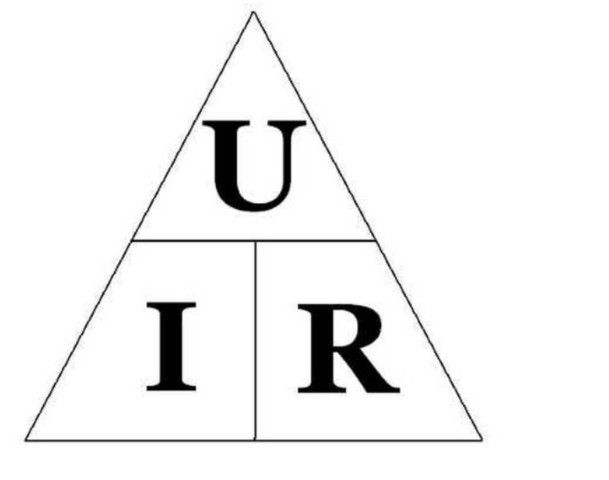
Мнемоническая схема

Согласно мнемосхеме, дабы рассчитать электросопротивление по закону ома для участка цепи неизменного тока, нужно всеохватывающее напряжение на участке цепи поделить на силу тока для полной цепи. Но, с физико-математической точки зрения, формулу ома для участка цепи для вычисления только по первому закону ома принято считать неполной.

Другой метод вычислить токовое сопротивление по закону ома коротко предполагает умножение электросопротивления материи, из которой выполнен проводник, на длину с последующим делением на площадь пересекающегося сечения.

Для выполнения вычислений сформулируйте по закону ома для участка цепи уравнение, исходя из имеющихся числовых данных:

Использование на полосы электропередач

В процессе доставки на линию электропередач энергопотери должны быть минимизированы. Предпосылкой энергетических утрат является нагрев провода, во время которого энергия электротока преобразуется в теплоэнергию.

Дабы дать определение по закону ома потерянной мощности, нужно показатель электрической мощности во 2-ой степени помножить на внутреннее сопротивление источника напряжения и поделить на ЭДС в квадрате.

Из этого следует, что рост утраты энергомощности осуществляется пропорционально протяжённости полосы электропередач и квадрату электродвижущей силы.

Какое освещение Вы предпочитаете
Встроенное Люстра

Так как электродвижущую силу ограничивает крепкость обмотки генератора, то увеличение энергонапряжения может быть после того, как из генератора выйдет электроток, на участке входа полосы.

Переменный ток легче всего распределяется по полосы через трансформатор. Но, так как следствием увеличения энергонапряжения является утрата коронирования, а надёжность изоляции обеспечивается с трудом, напряжение на участке цепи протяжённой полосы электропередач не превосходит миллиона вольт.

Внимание!

Поведение полосы электропередач в пространстве подобно антенне, ввиду чего берётся во внимание утрата на излучение.

Отображение в дифференциальной форме

На подсчёт сопротивления оказывает влияние тип материи, по которой протекает электроток, также геометрические габариты проводника.

Дифференциальная форма формулировки Ома, записывающаяся довольно коротко, показывает электропроводящие свойства изотропных материалов и заключается в умножении удельной проводимости на вектор напряжённости электрополя с целью вычисления вектора плотности энерготока.

Для выполнения требуемых вычислений, уравнение сформулируйте по закону ома:

Любопытно!

Если исходить из научных данных, следует прийти к выводу о законе ома в дифференциальной форме об отсутствии зависимого соотношения геометрических габаритов.

При использовании анизотропеновых электроэлементов часто встречается несовпадение вектора плотности токового энергонапряжения. Данное суждение справедливо для закона ома в интегральной и дифференциальной формах.

Переменный ток

Величины являются всеохватывающими, если речь идёт о синусоидальных формах энерготока с повторяющейся частотой, в цепях которых находятся активная ёмкость с индуктивностью.

В список всеохватывающих величин входят:

• разность между потенциалами;
• сила тока;
• всеохватывающее электросопротивление;
• модуль импеданса;
• разность индуктивного и ёмкостного сопротивлений;
• омическое электросопротивление;
• фаза импеданса.

Если несинусоидальный энерготок допустимо измерить временными показателями, закон ома для неполной электрической цепи может быть представлен в виде сложенных синусоидальных Фурье-компонентов. В линейной цепи составные элементы фурье-разложения являются независимо функционирующими. В нелинейных цепях образуются гармоники и огромное количество колебаний. Таким макаром, можно прийти к выводу о невозможности выполнения правила Ома для нелинейной электроцепи.

Внимание!

Гармоника – это колебание, частота которого кратна частоте напряжения.

Как трактуется правило Ома

Так как обобщённая формула ома не считается основополагающей, правило применяется для описания разновидностей проводников в критериях приближения малозначительной частоты, плотности тока и напряжения электрополя. Необходимо подчеркнуть, что в ряде всевозможных случаев как 1-ый закон, так и 2-ой закон, используемый для полной цепи, не соблюдаются.

Существует теория Друде, для выражения которой применяются следующие величины:

• удельная электропроводимость;
• концентрированное размещение электронов;
• показатель простого заряда;
• время затихания по импульсам;
• действенная масса электрона.

Внимание!

Все формулы Ома – 1-ый, 2-ой физический закон ома и 3-ий распространяются на омические составляющие.

Список критерий, при которых становится неосуществимым соблюдения правила Ома:

1. высочайшие частоты с чрезвычайно большой скоростью конфигурации электротока;
2. пониженная температура сверхпроводимого вещества;
3. перегрев проводника проходящим электротоком;
4. в ситуации пробоя, появившегося в итоге подсоединения к проводниковому элементу высокого напряжения;
5. в вакуумной либо газонаполненной электролампе;
6. для гетерогенного полупроводникового устройства;
7. при образовании пространственного диэлектрического заряда в контакте железного диэлектрика.

Интерпретация

Определяющаяся действием приложенного напряжения мощностная сила тока является пропорциональной показателю его напряжения. Например, при двойном увеличении приложенного напряжения, интенсивность неизменного тока также умножается.

Любопытно!

Более нередко правило Ома применяется для металла и керамики.

Способы запоминания формулы

Дабы легче уяснить формулу расчёта напряжения на участке цепи, следует выписать на картонном листе все величины, из которых она состоит, в которую также заходит сопротивление и сила тока. Разыскиваемую величину закрыть пальцем, вследствие чего соотношение оставшихся величин будет показывать действие, которое нужно совершить для её вычисления.

Ниже будет представлено видео с подробным разъяснением всех правил и формул, относящихся к рассматриваемой теме.

Закон Ома – один из самых легких для осознания, который заходит в программку школьных учебников физики исходного уровня. Пользуясь графическим приёмом расчёта величин – по мере надобности либо для самопроверки, можно получить безошибочные результаты вычислений.

Видео: Закон Ома для участка цепи. Электрическое сопротивление проводника. 8 класс.