Как было обозначено, под физическим полем понимается особенное состояние места вокруг вещества, проявляющееся в разработке силового воздействия на отменно схожее вещество в хоть какой точке этого места.
В согласовании с данным определением можно гласить о поле скоростей перемещающегося газа (к примеру, ветра на различных высотах), поле температур (при передаче тепла от какого-нибудь объекта), поле электрических либо магнитных сил, поле притяжения вещественных тел независимо от их природы (поле тяготения).
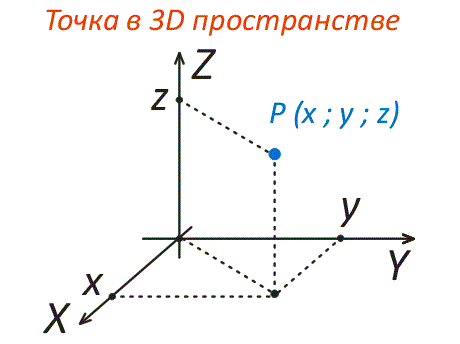
Физические поля есть в трехмерном пространстве и меняются во времени. Поэтому, их описание должно даваться функцией (либо функциями) 3-х координат (в декартовой системе) и времени. Анализ схожих выражений оказывается очень сложным. Потому по способности выражения упрощают, рассматривая разные личные случаи.
Исходя из убеждений зависимости от времени поля делят на статические, не зависящие от времени, стационарные, характеристики которых меняются во времени временами по известным зависимостям, и нестационарные, изменяющиеся во времени без повторяющегося повторения значений поля в отдельных точках места. Проще всего рассматривать статические и стационарные поля.
Исходя из убеждений пространственного воздействия на физические объекты поля делятся на скалярные и векторные.
Скалярное поле — это поле, параметр которого в каждой точке места задается одним числом. К примеру, рассредотачивание (поле) температуры железного бруска, нагреваемого с 1-го конца. В каждой точке бруска температура своя, но ее значение зависит только от координаты рассматриваемой точки и времени нагрева t и не находится в зависимости от какого-то выделенного направления. Потому, выбрав некоторую систему координат, температуру Т в хоть какой точке бруска можно представить как функцию координат (х, у, z) и времени V.
Представим, скалярное поле статично, т.е. значения температур в каждой точке бруска остаются постоянными во времени. Тогда можно соединить на уровне мыслей все точки равной температуры, они образуют поверхность равных температур. В каждой точке обозначенной
поверхности можно указать направление, по которому температура наращивается резвее всего. Снова подчеркнем, что идет речь не о повышении температуры во времени, а о росте (либо спаде) ее в пространстве при переходе от точки к точке. Обозначенное направление быстрейшего роста либо спада скалярного поля именуется градиентом (в уравнениях либо пишут grad Т, либо применяют особый символ Д Т).
Градиент как черта скорости пространственного нарастания поля содержит в себе производные по координатам, как черта направления является вектором. Совсем — градиент функции Т(х, у, z) есть вектор, проекциями которого на координатные оси служат значения личных производных этой функции.
В литературе принято обозначать направления координатных осей х, у, z единичными векторами, т.е. стрелками, направленными по подходящим координатным осям и длиной в одну единицу; эти единичные векторы обозначаются соответственно знаками *,у, к (векторы будут обозначаться жирным шрифтом). В обозначенных стандартных обозначениях градиент температурного поля запишется так:
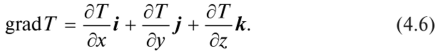
Подразумевается, что читатель знаком с простыми операциями над векторами, а именно знает, что сумма векторов есть вектор, приобретенный по правилу параллелограмма, а разность 2-ух векторов есть вектор, направленный от конца 1-го к концу другого.
Векторное поле — это поле, параметр воздействия на физические объекты которого в каждой точке места задается величиной и направлением деяния. Для описания векторного поля применяют два способа:
- • графический, когда значение поля в каждой точке места изображают в виде стрелки (вектора), направление которой указывает направление деяния поля в данной точке, а длина в условных единицах равна величине (модулю) поля в этой точке;
- • аналитический, в каком вектор обозначается или в виде выделенной жирным шрифтом буковкы (к примеру, сила /), или в виде буковкы, умноженной на вектор единичной длины. К примеру, выражение для импульса частички: р = m v п, где р — вектор импульса; m — масса частички (скаляр); v — модуль скорости частички (скаляр); п — единичный вектор скорости, т.е. вектор, модуль которого равен единице, а направление совпадает с направлением скорости частички.
Для полного уяснения правил изображения векторных полей и выполнения некоторых математических операций с векторами рас-
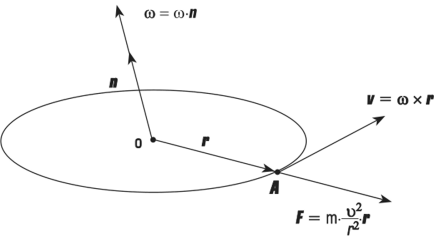
Рис. 4.1. Векторные поля вращающегося диска
смотрим точки на поверхности диска, вращающегося с неизменной угловой скоростью (рис. 4.1).
Выделим на поверхности диска некоторую точку А и проведем к ней из центра круга О радиус-вектор г, который не только лишь определяет малое расстояние от центра О до точки А, но и показывает в системе координат, связанной с диском, направление на точку А. Ясно, что г — вектор (имеет длину и определенное направление).
Относительно системы координат, не связанной с диском, видно, что радиус-вектор г крутится с неизменной периодичностью вокруг точки О, образуя стационарное векторное поле. Другими словами, все точки на радиусе-векторе г, описав угол 2я за время At, ворачиваются в начальное состояние; интервал времени At именуется периодом вращения.
Угол, на который поворачивается за единицу времени вектор г, именуется угловой скоростью вращения со. Отношение угла к интервалу времени со = 2n/At является, естественно, скаляром, но нужно каким-то образом указать, что вращение происходит не беспорядочно в трехмерном пространстве, а в определенной плоскости (в нашем случае — это плоская поверхность диска).
Плоскость, согласно аналитической геометрии, задается перпендикуляром единичной длины к ней, который обозначен на рис. 4.1 буковкой п. Совсем имеем: все точки диска, вращающегося с неизменным периодом At, образуют поле неизменной угловой скорости со = со п, при этом по договоренности вектор со ориентирован так, дабы, смотря с его конца на диск, видно было перемещение радиуса-вектора г против движения часовой стрелки.
Любая точка диска, не считая угловой скорости со, имеет и линейную скорость v, которую просто вычислить: за время 1-го периода At точка на диске проходит путь 2пг, поэтому, v = 2-кг/At. По

скольку со = 2nr/At, линейную скорость можно записать через угловую:
Но диск крутится, точка А на нем безпрерывно меняет свое положение, потому появляется вопрос: а куда же ориентирован вектор скорости? Он ориентирован, как просто обосновать, по касательной к окружности. Сама касательная перпендикулярна радиусу г в точке касания и лежит в плоскости диска, т.е. перпендикулярна вектору угловой скорости со.
Если вектор (а именно, скорости v) перпендикулярен плоскости, в какой лежат два других вектора (со и г), то знаком х (векторное умножение) обозначают операцию получения вектора, перпендикулярного плоскости, в какой лежат перемножаемые векторы, а модуль нового вектора равен произведению модулей начальных векторов, умноженному на синус угла между ними. В рассматриваемом случае можно, поэтому, записать вектор линейной скорости с учетом выражения (4.9) в виде

Если вспомнить, что точки на радиусе-векторе имеют разные модули (т.е. расстояния от оси вращения), то можно заключить: на вращающемся диске точки образуют поле линейных скоростей, направленных по касательной к окружности вращения в каждой точке и величиной (модулем), пропорциональной расстоянию от центра вращения до соответственной точки.

Непрерывное изменение направления линейной скорости v вращающейся точки А приводит к возникновению центростремительного ускорения а, равного по модулю а = v 2 /r и направленного по радиусу-вектору г. По второму закону Ньютона произведение массы вещественной точки т на ускорение (вектор) делает силу, направленную по направлению ускорения. На рис. 4.1 в формуле силы задание направления достигается умножением произведения массы т и модуля ускорения v 2 /r на вектор г. Но вектор г может быть хоть какой длины, потому умножение на него не только лишь показывает направление деяния силы, но изменяет и ее модуль. Дабы указать направление силы F и исключить воздействие длины вектора г, сразу с умножением на него выражение делится на длину (модуль) вектора г, что дает в конечном итоге
Мы разглядели поле скоростей и сил недвижных вещественных точек на вращающемся диске. А что будет, если по поверхности
вращающегося диска вещественная точка массой т движется с неизменной линейной скоростью vp вдоль радиуса-вектора #*? Как показано в курсах теоретической механики, в данном случае на точку действует сила, лежащая в плоскости вращения (т.е. перпендикулярная вектору угловой скорости со) и перпендикулярная вектору v . Сила эта по имени описавшего ее ученого именуется кориолисовой силой ^ив векторной форме равна

Векторные поля можно, естественно, обрисовать при помощи введения трехмерной системы координат, как это изготовлено для скалярного поля. Но схожее представление не очень комфортно: во-1-х, результаты вычислений оказываются зависимыми от избранных направлений осей координат; во-2-х, одному векторному уравнению соответствует три уравнения разложения вектора по координатным осям, что усложняет решение задач.
Потому обычно задачка формулируется в векторной форме, дальше перебегают к разложению векторов по координатным осям, но при всем этом направления осей подбирают так, дабы задачка имела обычное решение (к примеру, одну из осей направляют по постоянному направлению поля), а окончательный итог решения вновь обобщают в векторной форме.
Стационарные физические поля
В случае, когда каждую точку некоторой части места можно охарактеризовать физической величиной, можно гласить о физическом поле этой величины. К примеру, можно гласить о температурном поле в комнате, так как любая точка ее объема имеет температуру. Другой пример — поле сил, действующих на электрический заряд со стороны другого заряда. Разглядим физические поля, не зависящие от времени. Такие поля именуют стационарными. Главные законы, описывающие такие поля, следуют из законов сохранения. Так как источником той либо другой физической величины являются физические тела с определенными качествами (к примеру, источником электрического поля является заряженное тело), то для случайной области места без источников количество физической величины, попавшей в эту область, должно быть равным такому же количеству, вышедшему из нее. К примеру, температурное поле воздуха комнаты будет определяться законом сохранения энергии: источником (и поглотителем) термический энергии в комнате будут границы объема комнаты: нагревательные приборы, окна, пол, потолок, стенки и мебель. Для любого же объема снутри комнаты количество тепла, попавшего в него, должно приравниваться количеству тепла, из этого объема вышедшего. Все же, невзирая на обозначенную общность параметров стационарных физических полей, граничные условия для них определяются физической природой тел, и для различных полей они могут быть различными. Потому нередко нужно конкретизировать вид физического поля. В этом параграфе главные положения мы разберем на примере поля электрического тока в объеме проводника. Также тут мы снова будем применять вариационные принципы как основной метод получения уравнений.
Поля электрического тока в проводнике. Главные понятия
Электрический ток в точке г объема проводника характеризуется векторным полем плотности электрического тока j(г), направление которого есть направление движения электрических зарядов в этой точке, а величина

равна количеству электричества Q, протекающего за нескончаемо маленькое время dt через включающую эту точку нескончаемо малую плоскую площадку с площадью dS и с нормалью в направлении движения зарядов.
Также можно рассматривать довольно произвольные кусочногладкие поверхности в объеме проводника. Они будут характеризоваться потоком заряда — скалярной величиной, равной количеству электричества, протекающего через эту поверхность за единицу времени:

Тут ds — нескончаемо малый вектор элемента поверхности, его величина равна площади этого элемента поверхности, а ориентирован он перпендикулярно поверхности в данной точке. Для замкнутых поверхностей это направление выбирается «вне» замыкаемого поверхностью объема; для незамкнутых его указывают раздельно.
Предпосылкой направленного движения зарядов в проводнике служит электрическое поле с вектором напряженности Е(г), который можно выразить через поле электрического потенциала Ф(г):
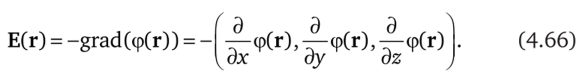
Поля Е(г) и j(г) связаны между собой законом Ома в дифференциальной форме:

где р(г) — удельное сопротивление материала проводника в точке г. Мы рассматриваем только изотропные проводники, у каких удельное сопротивление не находится в зависимости от направления плотности тока.
Разглядим граничные условия для задачи рассредотачивания электрического тока в проводящем теле (рис 4.4). Так как в нем течет ток, то есть две точки на его поверхности с различными потенциалами.
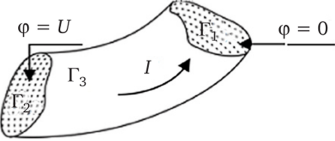
Рис. 4.4. Проводящее тело
При формулировке этой задачи обычно считается, что у проводящего тела есть целые участки поверхности, потенциалы на которых постоянны (Г и Г2 на рис. 4.4). Через другие участки поверхности (Г3) ток не течет. Граничными критериями являются или указание потенциалов на Г: и Г2, или указание полного тока I через проводник. При всем этом всегда учитывается как всепостоянство потенциалов на Г2 и Г2, так и непротекание тока через Г3.