Разглядим участок цепи, содержащий гальванический элемент либо аккумулятор, т. е. участок, на котором действуют посторонние силы. Таким участком является, к примеру, участок 1—2 (см. рис. 2.55). Выразим разность потенциалов φ1 — φ2 на концах этого участка через ЭДС E источника, его сопротивление г и силу тока I.
Для этого нужно поначалу избрать (произвольно) положительное направление обхода в контуре цепи и строго придерживаться правил символов, о которых мы гласили в § 2.2 и 2.11. Напомним их. Сила тока на рассматриваемом участке считается положительной, если направление тока (т. е. направление движения положительных зарядов) совпадает с избранным направлением. ЭДС считается положительной, если работа посторониих сил при перемещении единичного положительного заряда на данном участке цепи в направлении обхода положительна. (В случае гальванического элемента либо аккума ЭДС положительна, если этот заряд снутри источника перемещается от отрицательного электрода к положительному.) В конце концов, символ разности потенциалов φ1 — φ2 (либо напряжения U1,2) на данном участке находится в зависимости от того, что больше: φ1 либо φ2.
При избранном направлении обхода против часовой стрелки для цепи, изображенной на рисунке 2.55, I > 0, E > 0 и 1 — φ2 = U1,2 < 0, так как потенциал точки 1 (начало участка) — отрицательного полюса источника тока меньше потенциала точки 2 (конец участка) — положительного полюса.
Применяя закон Ома (2.14.5) для полной цепи, получим:

С другой стороны, применяя закон Ома (2.4.3) для участка цепи, не содержащего источник тока, а имеющего только резистор R (этот участок находится также между точками 1 и 2 в нижней части рис. 2.55), можно записать

Заменяя IR в формуле (2.15.1) на φ2 — φ1 из уравнения (2.15.2), получим:

Это и есть закон Ома для участка цепи, содержащего ЭДС. Разность потенциалов между началом и концом участка цепи равна падению напряжения на участке минус ЭДС этого участка.
При разомкнутой цепи I = 0 и, поэтому,
Таким макаром, ЭДС элемента равна разности потенциалов между его полюсами при разомкнутой цепи.
Дабы лучше осознать смысл формулы (2.15.3), разглядим тщательно два процесса — разрядку и зарядку аккума.
Разрядка аккума
На рисунке 2.57 штриховой линией выделен участок цепи с ЭДС. При избранном направлении обхода против часовой стрелки I > 0, E > 0, а U1,2 ≤ 0 (так как потенциал точки 1 — отрицательного полюса аккума меньше потенциала точки 2 — положительного полюса), т. е. электрические (кулоновские) силы совершают отрицательную работу. Потому уравнение (2.15.3) для модулей запишется так:

Напряжение равно ЭДС источника минус падение напряжения на участке (внутреннее падение напряжения).
Зарядка аккума
Схема зарядки аккума показана на рисунке 2.58. Выберем направление обхода контура по часовой стрелке. Тогда I > 0, U1,2 > 0 (так как φ1 > φ2), но E < 0.
Напряжение на аккуме сейчас больше его ЭДС на величину падения напряжения снутри аккума.
Закон Ома для участка цепи. Последовательное и параллельное соединение проводников. 10 класс. Физика.
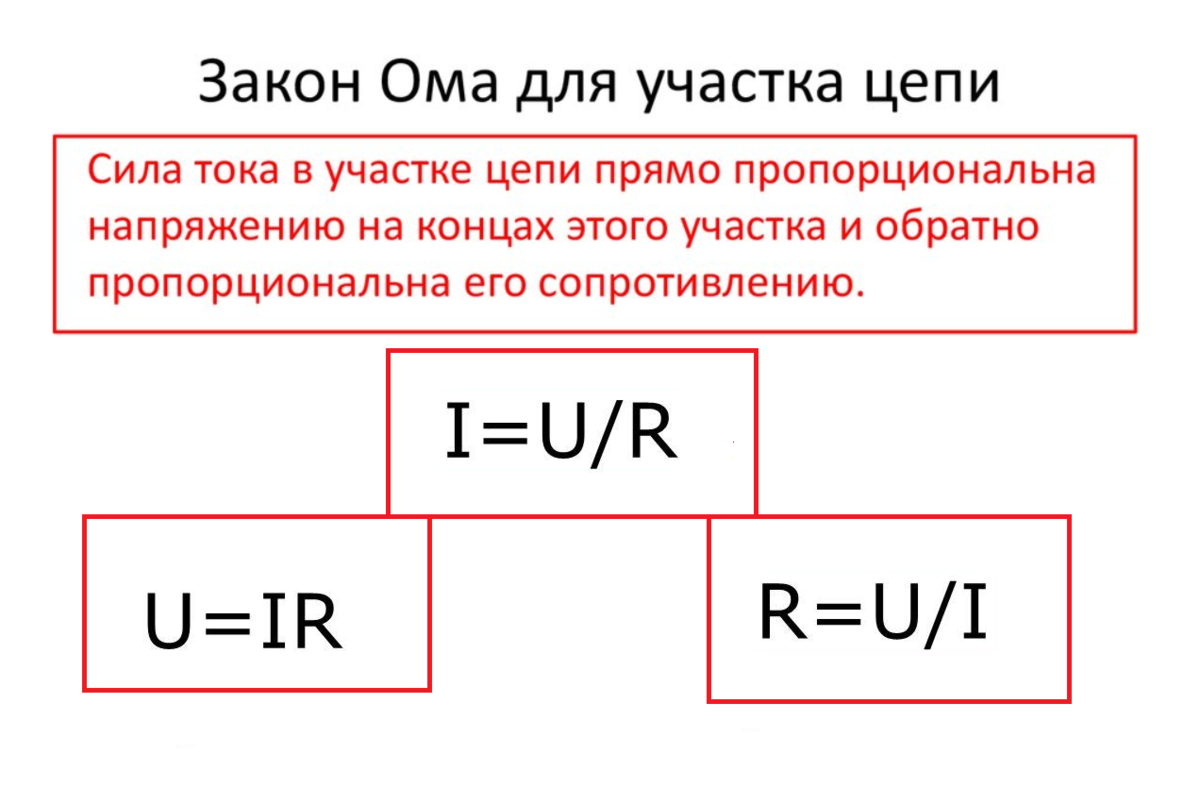
Сила тока на участке цепи прямо пропорциональна напряжению на этом участке и назад пропорциональна сопротивлению участка.
Закон Ома оказался справедливым не только лишь для металлов, но и для смесей электролитов. Сформулированный закон имеет место для так именуемого однородного участка цепи – участка, не содержащего источников тока.
Математическая запись закона Ома ординарна, как и его формулировка, но экспериментально подтвердить эту зависимость очень тяжело. Сила тока, протекающая по участку цепи, мала. Потому применяют довольно чувствительные приборы. Г. Ом сделал чувствительный устройство для измерения силы тока, а в качестве источника тока использовал термопару. Действие амперметра и вольтметра основано на использование закона Ома для участка цепи. Угол поворота стрелки устройства пропорционален силе тока.
Из математической записи закона Ома:
можно выразить напряжение :
и сопротивление проводника:
.
Таким макаром, закон Ома связывает три параметра, характеризующих неизменный электрический ток, проходящий по проводнику, и позволяет отыскивать хоть какой из них, если известны два других.
Закон Ома имеет границы применимости и осуществляется только в этом случае, когда при прохождении тока температура приметно не изменяется. На вольт–амперной характеристике лампы накаливания видно, что график сильно искривляется при напряжении выше 10В, означает, закон Ома выше этого напряжения использовать нельзя.
Также нельзя гласить, что сопротивление проводника находится в зависимости от напряжения и силы тока в цепи. Сопротивление участка цепи находится в зависимости от параметров проводника: длины, площади поперечного сечения и материала, из которого состоит проводник.
где l-длина проводника, s-его площадь поперечного сечения.
ρ –удельное сопротивление проводника – это физическая величина, характеризующая зависимость сопротивления проводника от материала, из которого он сделан.
Удельное сопротивление указывает, каким сопротивлением обладает изготовленный из этого вещества проводник длиной 1м и площадью поперечного сечения 1м2 .
Из формулы видно, что единицей измерения в системе СИ является Ом·м. Но так как площадь поперечного сечения проводника довольно мала, применяют единицы измерения
при вычислении площадь поперечного сечения проводника следует выражать в мм2.
В заключении охото увидеть, что Ом начал свои опыты, когда был учителем физики в гимназии. В собственных опытах Ом брал кусочки проволоки одинакового поперечника, но различного материала и изменял их длину таким макаром, дабы в цепи сила тока имела однообразное значение. Находящаяся вблизи магнитная стрелка отклонялась при прохождении тока в цепи. Установив связь между напряжением и силой тока, Г. Ом вывел один из главных законов неизменного тока.
Последовательное соединение проводников
Электрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из 1-го приёмника электрического тока, а из нескольких разных, которые могут быть соединены между собой по-разному. Зная сопротивление каждого и метод их соединения, можно высчитать общее сопротивление цепи.
На рисунке а изображена цепь последовательного соединения 2-ух электрических ламп, а на рисунке б — схема такового соединения. Если выключать одну лампу, то цепь разомкнётся и другая лампа погаснет.
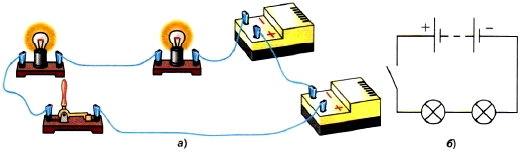
Рис. Последовательное включение лампочек и источников питания
Мы уже знаем, что при последовательном соединении сила тока в всех частях цепи одна и та же, т. е.
А чему равно сопротивление последовательно соединённых проводников?
Соединяя проводники последовательно, мы вроде бы увеличиваем длину проводника. Потому сопротивление цепи становится больше сопротивления 1-го проводника.
Последовательное соединение проводников
Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (либо отдельных участков цепи):
Напряжение на концах отдельных участков цепи рассчитывается на базе закона Ома:
U1 = IR1, U2 = IR2.
Из приведённых равенств видно, что напряжение будет огромным на проводнике с большим сопротивлением, так как сила тока всюду одинакова.
Полное напряжение в цепи при последовательном соединении, либо напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:
Это равенство вытекает из закона сохранения энергии. Электрическое напряжение на участке цепи измеряется работой электрического тока, совершающейся при прохождении по участку цепи электрического заряда в 1 Кл. Эта работа совершается за счёт энергии электрического поля, и энергия, израсходованная на всём участке цепи, равна сумме энергий, которые расходуются на отдельных проводниках, составляющих участок этой цепи.
Все приведённые закономерности справедливы для любого числа последовательно соединённых проводников.
Пример 1. Два проводника сопротивлением R1 = 2 Ом, R2 = 3 Ом соединены последовательно. Сила тока в цепи I = 1 А. Найти сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.
Запишем условие задачи и решим её.

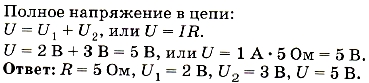
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ
Расчет характеристик электрической цепи
при параллельном соединении сопротивлений:
1. сила тока в неразветвленном участке цепи равна сумме сил токов
во всех параллельно соединенных участках
2. напряжение на всех параллельно соединенных участках цепи идиентично
3. при параллельном соединении сопротивлений складываются величины, оборотные сопротивлению :
( R — сопротивление проводника,
1/R — электрическая проводимость проводника)
Если в цепь включены параллельно только два сопротивления, то:
( при параллельном соединении общее сопротивление цепи меньше наименьшего из включенных сопротивлений )
4. работа электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме работ на отдельных участках:
A=A1+A2
5. мощность электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме мощностей на отдельных участках:
P=P1+P2
Для 2-ух сопротивлений:
т.е. чем больше сопротивление, тем меньше в нём сила тока.

Домашняя работа.
Задание 1. Ответить на вопросы.
- Какое соединение проводников именуют последовательным? Изобразите его на схеме.
- Какая электрическая величина одинакова для всех проводников, соединённых последовательно?
- Как отыскать общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?
- Как отыскать напряжение участка цепи, состоящего из последовательно соединённых проводников, зная напряжение на каждом?
- Какое соединение проводников именуют параллельным? Изобразите его на схеме.
- Какая из электрических величин одинакова для всех проводников, соединённых параллельно?
- Как выражается сила тока в цепи до её разветвления через силы токов в отдельных ветвях разветвления?
- Как меняется общее сопротивление разветвления после роста числа проводников в разветвлении?
- Какое соединение проводников применяется в жилых помещениях? Какие напряжения применяются для бытовых нужд?
Задание 2.Решите задачи.
1. Две лампочки соединены последовательно. Сила тока на первой лампочке 2А. Найдите общее напряжение и напряжение на каждой из ламп, если сопротивление на первой лампе 3Ом, а на 2-ой 4Ом.
2. Две лампочки соединены параллельно. Напряжение на 2-ой лампочке10В. Найдите силу тока в цепи и на каждой из ламп, если сопротивление на первой лампе 1Ом, а на 2-ой 2Ом.
К занятию прикреплен файл «Это любопытно». Вы сможете скачать файл в хоть какое комфортное вам время.
Обобщённый закон Ома. Закон Ома для участка цепи
больше .Тогда закон Ома для данного участка цепи будет иметь вид:
Обобщенный закон Ома.
1) (источник ЭДС – генератор)
2) (источник ЭДС – мотор)
Закон Ома для цепи, содержащей источник ЭДС (обобщенный закон Ома):
1-ый и 2-ой законы Кирхгофа. Расчёт электричес-кой цепи по законам Кирхгофа ( на примере электрической цепи).
1-ый закон Кирхгофа — алгебраическая сумма всех токов, сходящихся в узле равна нулю.
(Токи, направленные к узлу, условно принимаются отрицательными, а направленные от него -положительными). На
2-ой закон Кирхгофа — Вдоль замкнутого контура алгебраическая сумма падений напряжений в отдельных элементах контура равна алгебраической сумме ЭДС, входящих в этот контур (либо 0, если контур не содержит ЭДС)
Пример расчета цепи, основанного законах Кирхгофа:
· Число уравнений по первому закону Кирхгофа равно числу узлов минус 1
· Число уравнений по второму закону Кирхгофа равно числу независящих контуров:
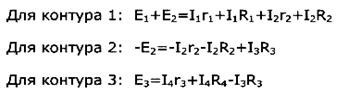
Последовательное, параллельное и смешанное соединение частей.
А) Последовательное соединение – это такое соединение, при котором через все элементы протекает один и тот же ток I=I1=I2=I3 , при всем этом U=U1+U2+U3= I1R1+I2R2+I3R3=I*(R1+R2+R3). Где Rэкв= R1+R2+R3
I*Rэкв=U
При последовательном соединении все сопротивления можно поменять одним эквивалентным.
Б) Параллельное соединение – при нем все элементы присоединяются к одной паре узлов, т.е. находятся под одним напряжением. I1=U1/R1; I2=U2/R2; I3=U3/R , тогда I=I1+I2+I3. Тогда U/Rэкв=U1/R1+U2/R2+U3/R3 а означает 1/Rэкв=1/ R1+1/R2+1/ R3, а I=U/Rэкв
В) Смешанное соединение – такое соединение частей, которое содержит последовательно и параллельно соединенные элементы. Rэкв=R1+R2+R6+R1R2R3/(R1R2+R2R3+R1R3)
Способ эквивалентных преобразований с одним источником.
Входные данные: R1, R2, R3, R4, R5,R6, E Отыскать: I.
R456=R4+R5+R6; R12=R1+R2; тогда преобразуем данную схему (рис.1) в эквивалентную (рис.2) с учетом этих преобразований.
R3456=(R3*R456)/(R3+R456). Исходя из этого преобразования преобразуем схему (рис.2) в эквивалентную (рис.3). I1=E/(R12+R3456)
I метод. Uab=E-I1R12; I2=Uab/R3; I3=Uab/R456.
II метод. В нем применяется формула «разброса». I2=I1*R456/(R3+R456); I3=I1*R3/(R3+R456)
В случае, когда в электрической цепи имеется источник тока, то для определения тока, то для определения тока в ветвях можно применять только формулу «разброса».
Способ контурных токов
уравнения способа контурных токов составляются только по второму закону Кирхгофа, но не для реальных, а для воображаемых токов, циркулирующих по замкнутым контурам, т.е. в случае выбора основных контуров равных токам веток связи. Число уравнений равно числу независящих контуров, т.е. числу веток связи графа . 1-ый закон Кирхгофа осуществляется автоматом. Контуры можно выбирать произвольно, только бы их число было равно и дабы каждый новый контур содержал хотя бы одну ветвь, не входящую в прошлые. Такие контуры именуются независящими.
Направления настоящих и контурных токов выбираются произвольно. Выбор положительных направлений до расчета может не определять действительные направления токов в цепи. Если в итоге расчета какой-нибудь из токов, как и при использовании уравнений по законам Кирхгофа, получится со знаком “-”, это значит, что его настоящее направление обратно.
При составлении уравнений нужно держать в голове следующее:
· — сумма сопротивлений, входящих в i-й контур;
· — сумма сопротивлений, общих для i-го и k-гоконтуров, при этом ;
· члены на главной диагонали всегда пишутся со знаком “+”;
· символ “+” перед остальными членами ставится в случае, если через общее сопротивление i-й и k- й контурные токи проходят в одном направлении, в неприятном случае ставится символ “-”;
· если i-й и k- й контуры не имеют общих сопротивлений, то ;
· в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в контур: со знаком “+”, если направление ЭДС совпадает с избранным направлением контурного тока, и “-”, если не совпадает.
Пример расчета цепи способом контурных токов
Пусть имеем схему по рис. 3.
Выразим токи веток через контурные токи:
Обойдя контур aeda, по второму закону Кирхгофа имеем:
Таким макаром, получили уравнение для первого контура относительно контурных токов. Аналогично можно составить уравнения для второго, третьего и 4-ого контуров
Вместе с первым решить их относительно контурных токов и потом по уравнениям, связывающим контурные токи и токи веток, отыскать последние.