Uk = RkIk — напряжение либо падение напряжения на k-м элементе контура.
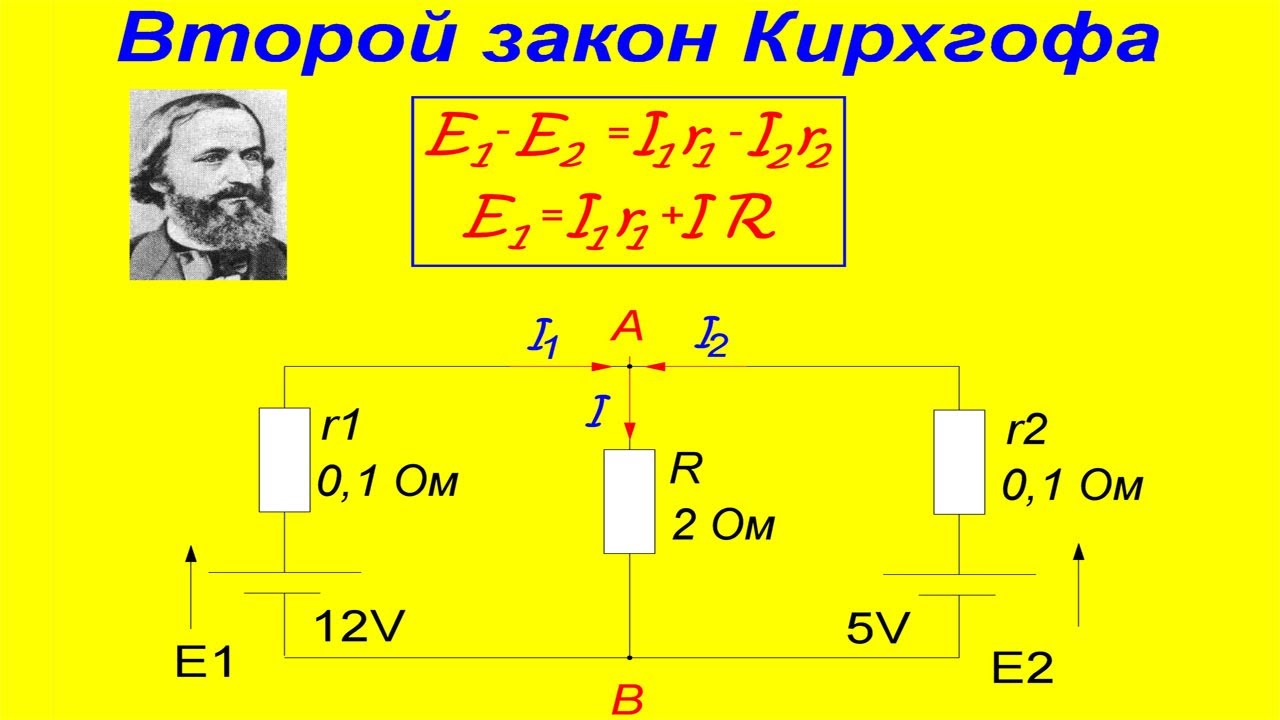
Для схемы (набросок 1) запишем уравнение по второму закону Кирхгофа:
Если в электрической цепи включены источники напряжений, то 2-ой закон Кирхгофа формулируется в следующем виде: алгебраическая сумма напряжений на всех элементах контуру, включая источники ЭДС равна нулю
При записи уравнений по второму закону Кирхгофа нужно:
- 1) задать условные положительные направления ЭДС, токов и напряжений;
- 2) избрать направление обхода контура, для которого записывается уравнение;
- 3) записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, при этом слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они обратны.
Запишем уравнения по II закону Кирхгофа для контуров электрической схемы (набросок 1)
контур I: E=RI+R1I1+r0I,
контур II: R1I1+R2I2=0,
контур III: E=RI+R2I2+r0I.
В действующей цепи электрическая энергия источника питания преобразуется в другие виды энергии. На участке цепи с сопротивлением R в течение времени t при токе I расходуется электрическая энергия
Скорость преобразования электроэнергии в другие виды представляет электрическую мощность.Из закона сохранения энергии следует, что мощность источников питания в хоть какой момент времени равна сумме мощностей, используемой на всех участках цепи.
Это соотношение именуют уравнением баланса мощностей. При составлении уравнения баланса мощностей следует учитывать, что если действительные направления ЭДС и тока источника совпадают, то источник ЭДС работает в режиме источника питания, и произведение EI подставляют в со знаком плюс. Если не совпадают, то источник ЭДС работает в режиме потребителя электроэнергии, и произведение EI подставляют в со знаком минус. Для цепи, показанной на рисунке 1 уравнение баланса мощностей запишется в виде:
Методы соединений и расчет эквивалентного сопротивления электрической цепи.
Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы на рисунке 2, где R=Rэкв, а расчет токов и напряжений делается при помощи законов Ома и Кирхгофа.
Электрическая цепь с последовательным соединением частей
Набросок 3
Набросок 4
Последовательным именуют такое соединение частей цепи, при котором во всех включенных в цепь элементах появляется один и тот же ток I (набросок 3).
На основании второго закона Кирхгофа общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
U=U1+U2+U3 либо IRэкв=IR1+IR2+IR3,
Таким макаром, при последовательном соединении частей цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Поэтому, цепь с хоть каким числом последовательно включенных сопротивлений можно поменять обычной цепью с одним эквивалентным сопротивлением Rэкв (набросок 4). После чего расчет цепи сводится к определению тока I всей цепи по закону Ом и по вышеприведенным формулам рассчитывают падение напряжений U1,U2,U3 на соответственных участках электрической цепи (набросок 3).
Недочет последовательного включения частей состоит в том, что при выходе из строя хотя бы 1-го элемента, прекращается работа всех других частей цепи.
Электрическая цепь с параллельным соединением частей
Параллельным именуют такое соединение, при котором все включенные в цепь потребители электроэнергии, находятся под одним и этим же напряжением (набросок 5).
В данном случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных веток:
I=I1+I2+I3, т.е. откуда следует, что
В этом случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением.
Из соотношения, следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных веток:
По мере роста числа параллельно включенных потребителей проводимость цепи gэкв увеличивается, и напротив, общее сопротивление Rэкв миниатюризируется.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (набросок 5)
Отсюда следует, что т.е. ток в цепи распределяется между параллельными ветвями назад пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители хоть какой мощности, рассчитанные на одно и то же напряжение. При этом включение либо отключение 1-го либо нескольких потребителей не отражается на работе других. Потому эта схема является основной схемой подключения потребителей к источнику электроэнергии.
Электрическая цепь со смешанным соединением частей
Смешанным именуется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.
Для цепи, представленной на рисунке 6, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно:
В данном случае начальную схему (набросок 6) можно представить в следующем виде (набросок 7):
На схеме (набросок 7) сопротивление R3 и Rcd соединены последовательно, тогда и сопротивление участка цепи ad равно:
Тогда схему (набросок  можно представить в сокращенном варианте (набросок 9):
можно представить в сокращенном варианте (набросок 9):
На схеме (набросок  сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно
сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно
Схему (набросок  можно представить в облегченном варианте (набросок 9), где сопротивления R1 и Rab включены последовательно.
можно представить в облегченном варианте (набросок 9), где сопротивления R1 и Rab включены последовательно.
Тогда эквивалентное сопротивление начальной схемы (набросок 6) будет равно:
Набросок 9
Набросок 10
В итоге преобразований начальная схема (набросок 7) представлена в виде схемы (набросок 10) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех частей схемы можно произвести по законам Ома и Кирхгофа.
Набросок 1.1 Схема рассчитываемой цепи неизменного тока
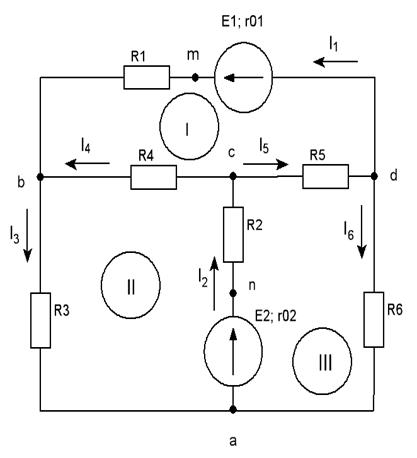
R1 = 52Ом, R2=24Ом,
r01 = 1 Ом, r02=2 Ом.
Найти токи во всех ветвях схемы, используя способ контурных токов.
Способ контурных токов основан на использовании только второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе на n — 1 .
Достигается это разделением схемы на ячейки (независящие контуры) и введением для каждого контура-ячейки собственного тока — контурного тока, являющегося расчетной величиной.
Итак, в данной цепи (рис. 1.1) можно разглядеть три контура-ячейки (1, 2, 3) и ввести для них контурные токи Ik1, Ik2, Ik3.
Контуры-ячейки имеют ветвь, не входящую в другие контуры — это наружные ветки. В этих ветвях контурные токи являются действительными токами веток.
Ветки, принадлежащие двум смежным контурам, именуются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления.
При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур-ячейку, в правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, также учитывается падение напряжения на сопротивлениях смежной ветки, определяемое по контурному току примыкающего контура.
На основании вышеизложенного порядок расчета цепи способом контурных токов будет следующим:
стрелками указываем избранные направления контурных токов Ik1, Ik2, Ik3 в контурах-ячейках. Направление обхода контуров принимаем таким же;
составляем уравнения и решаем систему уравнений либо способом подстановки,
либо при помощи определителей.
- -E1=Ik1·(R1+r01+ R4 +R5)-Ik2· R4-Ik3·R5
- -E2=-Ik2·(R2+r02+R3+ R4)-Ik1·R4-Ik3·(R2+r02)
E2=Ik3·( R2+r02+R5+R6)-Ik1·R5-Ik2· (R2+r02)
Подставляем в уравнение численные значения ЭДС и сопротивлений.
- -40=Ik1·(52+1+36+61)-Ik2·36-Ik3·61
- -30=Ik2·(24+2+43+36)-Ik1·36-Ik3·(24+2)
- 30=Ik3·(24+2+61+16)-Ik1·61-Ik2·(24+2)
- -40=Ik1·150-Ik2·36-Ik3·61
- -30=Ik2·105-Ik1·36-Ik3·26
- 30=Ik3·103-Ik1·61-Ik2·26
- -40=Ik1·150-Ik2·36-Ik3·61
- -30=- Ik1·36+Ik2·105-Ik3·26
- 30=-Ik1·61-Ik2·26+Ik3·103
Решим систему при помощи определителей. Вычислим определитель системы ? и чaстные определители ?1, ?2, ?3.
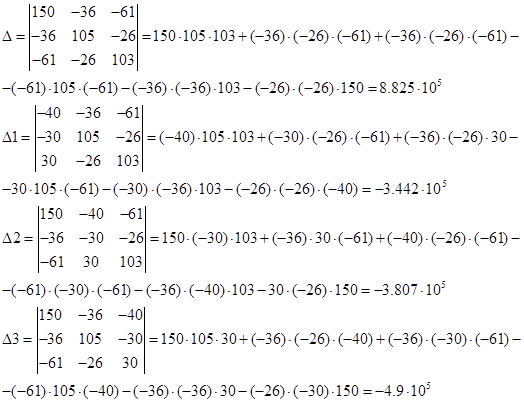
Вычисляем контурные токи:
Тогда токи веток будут равны:
I2= Ik3- Ik2= -0.049+0.431=0.383 А
I4= Ik1 -Ik2= -0.39+0.431=0.041 А
I5= Ik3 -Ik1= -0.049+0.39=0.341 А
Найти токи во всех ветвях схемы на основании способа наложения.
По способу наложения ток в любом участке цепи рассматривается как алгебраическая сумма личных токов, сделанных каждой ЭДС в отдельности.
а) Определяем личные токи от ЭДС Е1, при отсутствии ЭДС Е2, т.е. рассчитываем цепь по рис. 1.2.
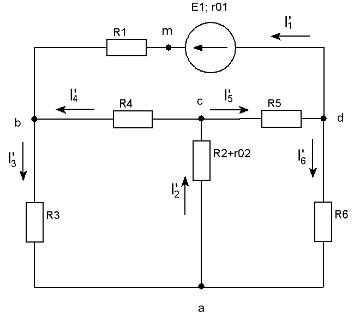
Рис 1.2. Схема цепи при выведенном E2
Показываем направление личных токов при ЭДС Е1 и обозначаем буковкой I с одним штрихом(`).
Решаем задачку способом "свёртывания".
Преобразовываем треугольник сопротивлений R2-R3-R4 в эквивалентную звезду Rb/- Rc/- Rd/.
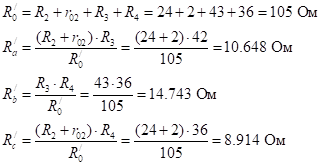
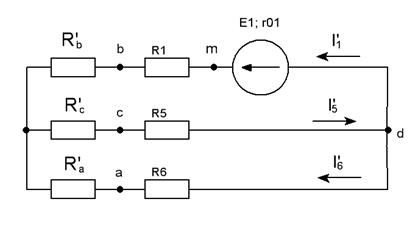
Рис 1.2.2 Перевоплощенная схема при выведенном E2
б) определяем личные токи от ЭДС Е2, при отсутствии ЭДС Е1, т.е. рассчитываем цепь по рис.1.3
Показываем направление личных токов при ЭДС Е2 и обозначаем их буковкой I с 2-мя штрихами (“).
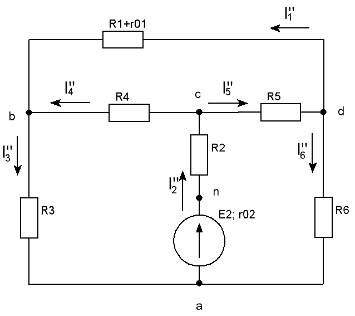
Рис 1.3. Схема цепи при выведенном E1
Рис 1.3.2 Перевоплощенная схема при выведенном E1
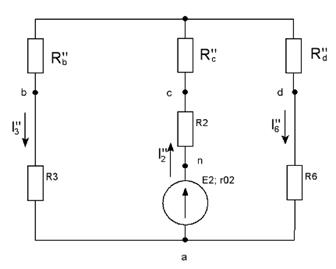
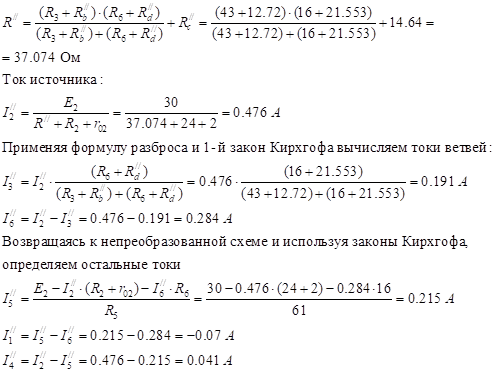
Вычисляем токи веток начальной цепи (рис. 1.1), выполняя алгебраическое сложение личных токов, беря во внимание их направление:

Составить баланс мощностей для данной схемы.
Источники Е1 и Е2 вырабатывают электрическую энергию, т.к. направление ЭДС и тока в ветвях с источником совпадают. Баланс мощностей для данной цепи запишется так:
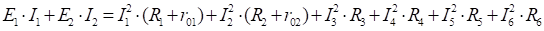
Подставляем численные значения и вычисляем:
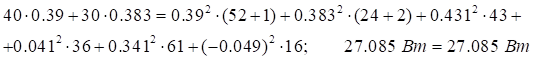
С учетом погрешности расчетов баланс мощностей вышел.
Результаты расчетов токов по пт 2 и 3 представить в виде таблицы и сопоставить.
Законы Кирхгофа и их использование
Для расчета разветвленной сложной электрической цепи существенное значение имеет число веток и узлов.
Ветвью электрической цепи и ее схемы именуется участок, состоящий только из последовательно включенных источников ЭДС и приемников с одним и этим же током. Узлом цепи и схемы именуется место либо точка соединения 3-х и поболее веток (узлом время от времени именуют и точку соединения 2-ух веток).
При обходе по соединенным в узлах веткам можно получить замкнутый контур электрической цепи; каждый контур представляет собой замкнутый путь, проходящий по нескольким веткам, при всем этом каждый узел в рассматриваемом контуре встречается менее 1-го раза.

На рис. 1.13 в качестве примера показана схема электрической цепи с пятью узлами и девятью ветвями. В личных случаях встречаются ветки только с резистивными элементами без источников ЭДС (ветвь 1 — у) и с сопротивлениями, фактически равными нулю (ветвь 2 — р). Так как напряжение между выводами ветки 2 — р равно нулю (сопротивление равно нулю), то потенциалы точек 2 и р одинаковы и оба узла можно соединить в один.
Режим электрической цепи случайной конфигурации вполне определяется первым и вторым законами Кирхгофа.
1-ый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна пулю:
В этом уравнении однообразные знаки должны быть взяты для токов, имеющих однообразные положительные направления относительно узловой точки. В предстоящем будем в уравнениях, составленных по первому закону Кирхгофа, записывать токи, направленные к узлу, с отрицательными знаками, а направленные от узла, — с положительными.
Если к данному узлу присоединен источник тока, то ток этого источника также должен быть учтен. В предстоящем будет показано, что в ряде всевозможных случаев целенаправлено писать в одной части равенства (1.19а) алгебраическую сумму токов в ветвях, а в другой части алгебраическую сумму токов, обусловленных источниками токов:
где I — ток одной из веток, присоединенной к рассматриваемому узлу, a J — ток 1-го из источников тока, присоединенного к тому же самому узлу; этот ток заходит в (1.196) с положительным знаком, если ориентирован к узлу, и с отрицательным, если ориентирован от узла.
2-ой закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом контуре алгебраическая сумма напряжений на всех элементах и участках цепи, входящих в этот контур, равна нулю :
при всем этом положительные направления для напряжений на элементах и участках выбираются произвольно; в уравнении (1.20а) положительные знаки принимаются для тех напряжений, положительные направления которых совпадают с произвольно избранным направлением обхода контура.
Нередко применяется другая формулировка второго закона Кирхгофа: в любом замкнутом контуре алгебраическая сумма напряжений на всех участках с сопротивлениями, входящими в этот контур, равна алгебраической сумме ЭДС :
В этом уравнении положительные знаки принимаются для токов и ЭДС, положительные направления которых совпадают с произвольно избранным направлением обхода рассматриваемого контура.
В теории электрических цепей решаются задачи 2-ух типов. К первому типу относятся задачи анализа электрических цепей, когда, к примеру, известны конфигурация и элементы цепи, а нужна найти токи, напряжения и мощности тех либо других участков. Ко второму типу относятся оборотные задачи, в каких, к примеру, заданы токи и напряжения на некоторых участках, а нужна отыскать конфигурацию цепи и избрать ее элементы. Такие задачи именуются задачками синтеза электрических цепей. Отметим, что решение задач анализа намного проще решения задач синтеза.
В практической электротехнике достаточно нередко встречаются задачи анализа. Не считая того, для овладения приемами синтеза цепей нужно за ранее изучить способы их анализа, которые в большей степени и будут в предстоящем рассматриваться.
Задачи анализа могут быть решены с помощью законов Кирхгофа. Если известны характеристики всех частей цепи и ее конфигурация, а нужна найти токи, то при составлении уравнений по законам Кирхгофа рекомендуется придерживаться таковой последовательности: поначалу избрать произвольные положительные направления токов во всех ветвях электрической цепи, потом составить уравнения для узлов на основании первого закона Кирхгофа и, в конце концов, составить уравнения для контуров на основании второго закона Кирхгофа.
Пусть электрическая цепь содержит В веток и У узлов. Покажем, что на основании первого и второго законов Кирхгофа можно составить соответственно У — 1 и В — У + 1 взаимно независящих уравнений, что в сумме дает нужное и достаточное число уравнений для определения В токов (во всех ветвях).
На основании первого закона Кирхгофа для У узлов (рис. 1.13) можно написать У уравнений:

Так как неважно какая ветвь связывает между собой только два узла, то ток каждой ветки должен непременно войти в эти уравнения 2 раза, при этом I12 =-I21 ; I13 =-I31 и т.д.
Поэтому, сумма левых частей всех У уравнений дает тождественно нуль. По другому говоря, одно из У уравнений может быть получено как следствие других У — 1 уравнений либо число взаимно независящих уравнений, составленных на основании первого закона Кирхгофа, равно У — 1, т. е. на единицу меньше числа узлов. К примеру, в случае цепи по рис. 1.14,о с 4-мя узлами
Добавим к этим У — 1 = 3 уравнениям уравнение
Суммируя четыре уравнения, получаем тождество 0 = 0; поэтому, из этих 4 уравнений любые три независящие, к примеру 1-ые три (1.21а).
Так как безграничное скопление электрических зарядов не может происходить как в отдельных узлах электрической цепи, так и в всех ее частях, ограниченных замкнутыми поверхностями, то 1-ый закон Кирхгофа можно применить не только лишь к какому-либо узлу, но и к хоть какой замкнутой поверхности — сечению.
К примеру, для поверхности S (рис. 1.14,а), вроде бы рассекающей электрическую схему на две части, справедливо уравнение , что можно также получить из уравнений (1.21) для узлов 3 и 4.
Дабы установить число взаимно независящих уравнений, вытекающих из второго закона Кирхгофа, напишем для всех В веток схемы (рис. 1.13) В уравнений на основании закона Ома (1.11а):
где — сопротивление ветки, соединяющей узлы р и у; Е ру — суммарная ЭДС, действующая в ветки р — у в направлении от р к у; — потенциалы узлов р и у.
В этих уравнениях суммарное число неведомых токов В веток и потенциалов У узлов приравнивается В + У.
Не меняя критерий задачи, можно принять потенциал 1-го из узлов равным хоть какому значению, а именно нулю. Если сейчас из системы В уравнений (1.22) исключить оставшиеся неведомыми У — 1 потенциалов, то число уравнений уменьшится до В — (У — 1). Но исключение потенциалов из уравнений (1.22) приводит к уравнениям, связывающим ЭДС источников с напряжениями на резистивных элементах, т. е. к уравнениям, составленным на основании второго закона Кирхгофа.
Таким макаром, число независящих уравнений, которые можно составить на основании второго закона Кирхгофа, равно В — (У- 1).
В качестве примера напишем уравнения, связывающие потенциалы узлов с токами и ЭДС для схемы рис. 1.14, а по ( 1.126):
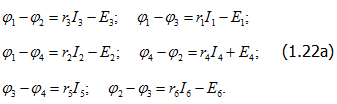
Сложив третье и 4-ое уравнения и вычтя полученную сумму из первого, получим
Если применим 2-ой закон Кирхгофа (1.206) к контуру 1-4-2-1 (при обходе вдоль контура по направлению движения часовой стрелки), то получим это уравнение.
Аналогичным методом можно получить уравнения для других контуров:
для контура 1-3-2-1
для котуpa 2-4-3-2
Совместное решение всех 5 уравнений (1.21), (1.23) и (1.24) дает значения токов во всех ветвях электрической цепи, показанной на рис. 1.14, а. Если и итоге решения этих уравнений получится отрицательное значение для какого-нибудь тока, то это означает, что действительное направление обратно принятому за положительное.
При записи уравнений по второму закону Кирхгофа следует обращать повышенное внимание на то, дабы составленные уравнения были взаимно независящими. Контуры нужно избрать гак. дабы в них вошли все ветки схемы, а в любой из контуров — может быть наименьшее число веток. Контуры взаимно независимы, если каждый последующий контур, для которого составляется уравнение, имеет не меньше одной новейшей ветки и не выходит из контуров, для которых уже написаны уравнения, методом удаления из этих контуров общих веток. К примеру, контур 1-3-4-2-1 (рис. 1.14, а) можно получить из контуров 1-3-4-1 и 1-4-2-1 методом удаления ветки 1-4. Потому уравнение для контура 1-3-4-2-1 является следствием уравнений (1.23), (1.24а) и выходит методом их суммирования. Дальше будет входные данные более общепринятое правило выбора контуров, обеспечивающих получение независящих уравнений.
Вторым законом Кирхгофа можно воспользоваться для определения напряжения между 2-мя случайными точками схемы. В данном случае нужно ввести в левую часть уравнений (1.20) разыскиваемое напряжение вдоль пути, вроде бы дополняющего незамкнутый контур до замкнутого. К примеру, для определения напряжения U 52 (рис. 1.14, а) можно написать уравнение для контура 2-1-5-2
либо для контура 5-4-2-5
откуда просто отыскать разыскиваемое напряжение.
Пример 1.2.
Пользуясь законами Кирхгофа, написать два выражения для тока I 0 в ветки с гальванометром (рис. 1.15), приняв известным в одном случае ток I , а в другом напряжение U .
Решение.
На основании законов Кирхгофа напишем для данной схемы с шестью неведомыми токами уравнения:
Решив вместе эти уравнения, получим выражения для тока I 0 при данном напряжении U
и при данном токе I
Для полной свойства электрического состояния цепи нужно знать не только лишь токи и напряжения, но также мощности источников и приемников энергии.
В согласовании с законом сохранения энергии развиваемая всеми источниками мощность равна суммарной мощности приемников и мощности утрат в источниках (из-за внутренних сопротивлений)
В левой части (1.25) суммы алгебраические. Это означает, что если при данных направлениях деяния источника ЭДС (см. рис. 1.7) либо тока (см. рис. 1.8) для тока I в источнике ЭДС либо напряжения U 12 на выводах источника тока получится отрицательное численное значение, то этот источник в реальности не разовьет мощность, а получит ее от других источников. Соответственное слагаемое в левой части (1.25) получится со знаком минус. Если нужна отыскать нужную мощность источников питания цепи, то такие слагаемые следует записать с оборотным знаком в правой части (1.25).
Правило напряжений Кирхгофа (2-ой закон Кирхгофа)
Что такое правило напряжений Кирхгофа (2-ой закон Кирхгофа)?
Принцип, узнаваемый как правило напряжений Кирхгофа (открытое в 1847 году германским физиком Густавом Р. Кирхгофом), можно сконструировать следующим образом:
«Алгебраическая сумма всех напряжений в замкнутом контуре равна нулю»
Под алгебраической я подразумеваю, кроме учета величин, учет и символов (полярностей). Под контуром я подразумеваю хоть какой путь, прослеживаемый от одной точки в цепи до других точек в этой цепи, и, в конце концов, назад в начальную точку.
Демонстрация закона напряжений Кирхгофа в последовательной цепи
Давайте снова поглядим на наш пример последовательной схемы, сейчас нумеруя точки цепи для обозначения напряжений:
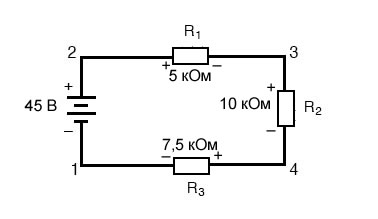
Набросок 1 – Демонстрация закона напряжений Кирхгофа в последовательной цепи
Если б мы подключили вольтметр между точками 2 и 1, красный измерительный провод к точке 2 и черный измерительный провод к точке 1, вольтметр зарегистрировал бы значение +45 вольт. Для положительных показаний на мониторах цифровых счетчиков символ «+» обычно не отображается, а быстрее предполагается. Но для этого урока полярность показаний напряжений очень принципиальна, потому я буду очевидно демонстрировать положительные числа:
Когда напряжение указывается с двойным нижним индексом (знаки «2-1» в обозначении «E2-1»), это значит напряжение в первой точке (2), измеренное по отношению ко 2-ой точке (1). Напряжение, обозначенное как «Ecd», будет означать значение напряжения, показанное цифровым мультиметром с красным измерительным проводом в точке «c» и черным измерительным проводом в точке «d»: напряжение в точке «c» относительно точки «d».
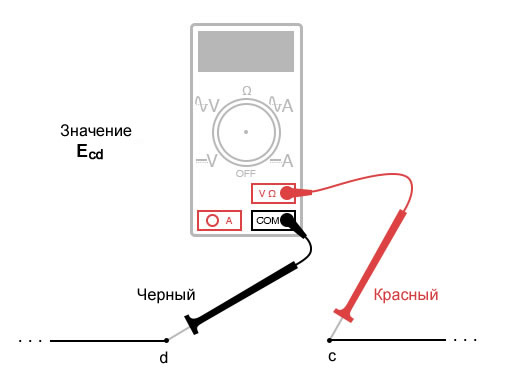
Набросок 2 – Значение Ecd
Если б мы взяли тот же вольтметр и измерили падение напряжения на каждом резисторе, обходя цепь по часовой стрелке с красным измерительным проводом нашего мультиметра на точке впереди и черным измерительным проводом на точке сзади, мы получили бы следующие показания:
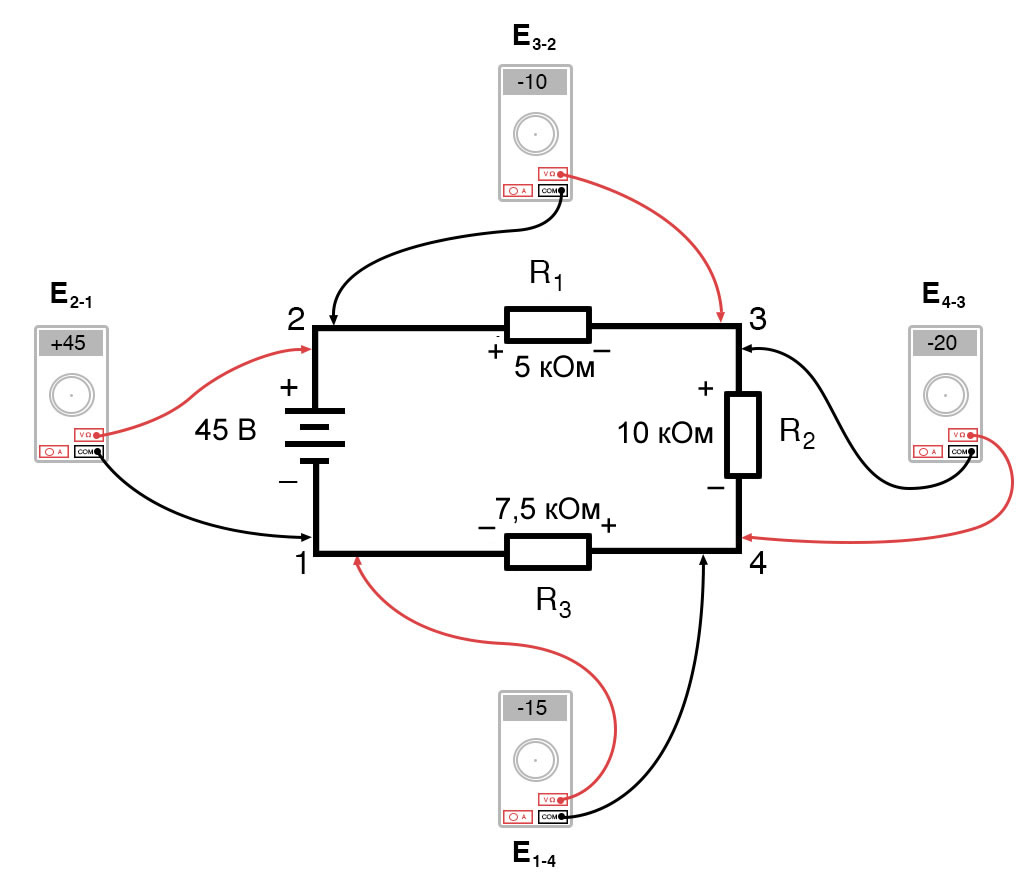
Набросок 3 – Определение напряжений в последовательной цепи
Нам уже должен быть знаком общий для последовательных цепей принцип, утверждающий, что отдельные падения напряжения в сумме составляют общее приложенное напряжение, но измерение падения напряжения таким макаром и уделение внимания полярности (математическому знаку) показаний открывает очередной нюанс этого принципа: все измеренные напряжения в сумме равны нулю:
В приведенном выше примере контур образован следующими точками в следующем порядке: 1-2-3-4-1. Не имеет значения, с какой точки мы начинаем либо в каком направлении движемся при следовании по контуру; сумма напряжений как и раньше будет равна нулю. Дабы показать это, мы можем той же цепи подсчитать напряжения в контуре 3-2-1-4-3:
Этот пример может быть более понятен, если мы перерисуем нашу последовательную схему так, дабы все составляющие были представлены на одной прямой полосы:
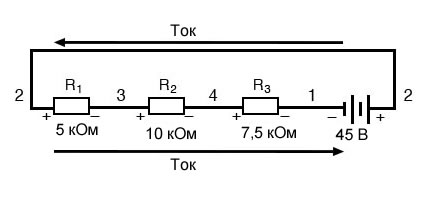
Набросок 4 – Изменение представления последовательной цепи
Это всё та же последовательная схема, только с малость перераспределенными компонентами. Направьте внимание на полярность падений напряжения на резисторах по отношению к напряжению батареи: напряжение батареи отрицательное слева и положительное справа, тогда как все падения напряжения на резисторах нацелены в другую сторону (положительное слева и отрицательное справа). Это так как резисторы сопротивляются сгустку электрического заряда, проталкиваемого батареей. Другими словами, «толкание», прилагаемое резисторами против потока электрического заряда, должно происходить в направлении, обратном источнику электродвижущей силы.
Тут мы лицезреем, что цифровой вольтметр покажет на каждом компоненте в этой цепи, если черный провод будет слева, а красный провод – справа:
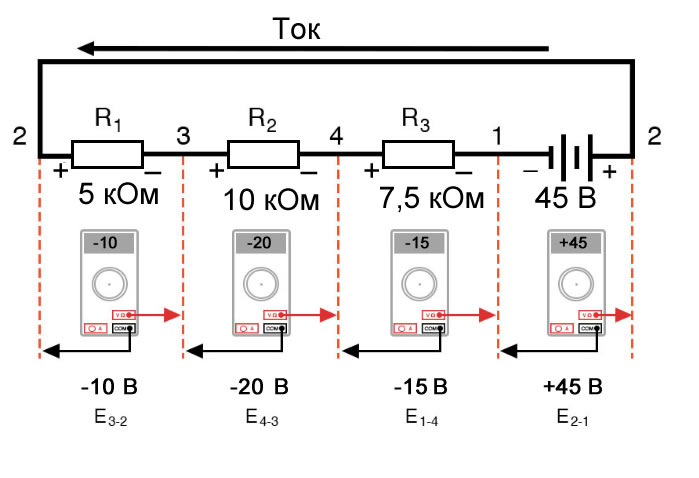
Набросок 5 – Измерение напряжений в последовательной цепи
Если б мы взяли тот же вольтметр и измерили напряжение между комбинациями компонент, начиная с единственного R1 слева и продвигаясь по всей цепочке компонент, мы узрели бы, как напряжения складываются алгебраически (до нуля):
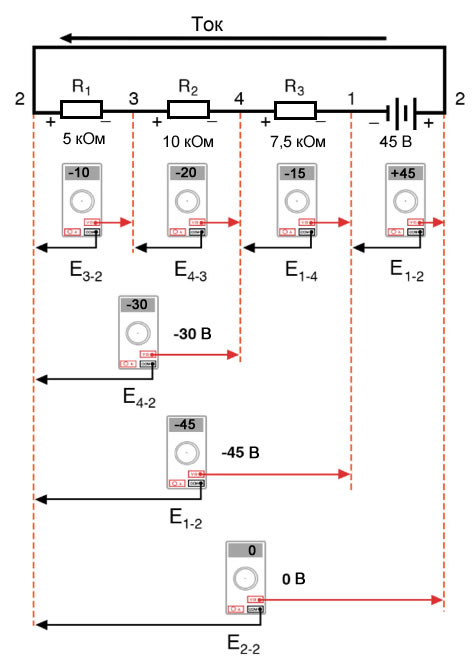
Набросок 6 – Измерение суммы напряжений в последовательной цепи
Тот факт, что последовательные напряжения складываются, не должен быть потаенной, но мы увидели, что полярность этих напряжений имеет огромное значение в том, как эти значения складываются. При измерении напряжения на R1 – R2 и R1 – R2 – R3 (я использую знак «двойное тире» «–» для обозначения последовательного соединения между резисторами R1, R2 и R3), мы лицезреем, как измеряются бо́льшие значения напряжений (хотя и отрицательные), так как полярности отдельных падений напряжения имеют одинаковую ориентацию (плюс слева, минус справа).
Сумма падений напряжения на R1, R2 и R3 равна 45 вольт, что соответствует выходному напряжению батареи, кроме того, что полярность напряжения батареи (минус слева, плюс справа) обратна падениям напряжения на резисторах, потому при измерении напряжения на всей цепочке компонент мы получаем 0 вольт.
То, что мы должны получить ровно 0 вольт на всей полосы, тоже не должно быть потаенной. Смотря на схему, мы лицезреем, что последняя левая часть полосы (левая сторона R1, точка номер 2) впрямую соединена с последней правой частью полосы (правая сторона батареи, точка номер 2), что нужно для окончания схемы.
Так как эти две точки соединены впрямую, они являются электрически общими вместе. Таким макаром, напряжение между этими 2-мя электрически общими точками должно быть равно нулю.
Демонстрация закона напряжений Кирхгофа в параллельной цепи
Правило напряжений Кирхгофа (2-ой закон Кирхгофа) будет работать вообщем для хоть какой конфигурации схемы, а не только лишь для обычных последовательных цепей. Направьте внимание, как это работает для следующей параллельной схемы:
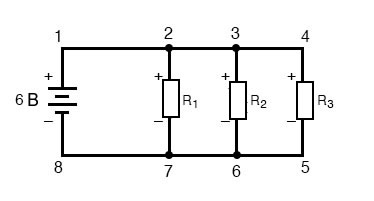
Набросок 7 – Параллельная схема из резисторов
При параллельной схеме напряжение на каждом резисторе равно напряжению питания: 6 вольт. Суммируя напряжения вдоль контура 2-3-4-5-6-7-2, мы получаем:
Направьте внимание, что конечное (суммарное) напряжение я обозначил как E2-2. Так как мы начали наше пошаговое прохождение по контуру в точке 2 и окончили в точке 2, алгебраическая сумма этих напряжений будет таковой же, как напряжение, измеренное между той же точкой (E2-2), которое, естественно, должно быть равно нулю.
Справедливость закона Кирхгофа о напряжениях независимо от топологии цепи
Тот факт, что эта цепь является параллельной, а не последовательной, не имеет ничего общего со справедливостью закона Кирхгофа о напряжениях. Тут схема может быть «черным ящиком» (конфигурация ее компонент стопроцентно укрыта от нашего взора) с набором открытых клемм, между которыми мы можем измерить напряжение, – и правило напряжений Кирхгофа всё равно остается верным:
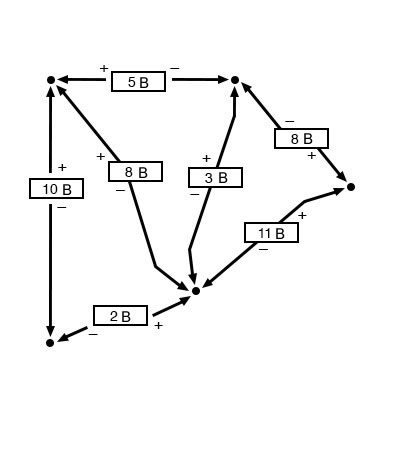
Набросок 8 – Справедливость закона Кирхгофа напряжениях независимо от топологии схемы
Попытайтесь на приведенной выше диаграмме выполнить обход в любом порядке, начиная с любого вывода, и возвратившись к начальному выводу, и вы обнаружите, что алгебраическая сумма напряжений всегда равна нулю.
Более того, «контур», который мы отслеживаем для второго закона Кирхгофа, даже не непременно должен быть реальным методом протекания тока в прямом смысле этого слова. Всё, что нам необходимо выполнить, дабы соответствовать правилу напряжений Кирхгофа, – это начинать и заканчивать в одной и той же точке цепи, подсчитывая падения напряжения и полярности при переходе между точками. Разглядим следующий абсурдный пример, проходя по «контуру» 2-3-6-3-2 в той же параллельной резисторной цепи:

Набросок 9 – Параллельная схема из резисторов
Внедрение закона Кирхгофа о напряжениях в сложной цепи
Закон Кирхгофа о напряжениях можно применять для определения неведомого напряжения в сложной цепи, где известны все другие напряжения вдоль определенного «контура». В качестве примера возьмем следующую сложную схему (по сути две последовательные цепи, соединенные одним проводом понизу):
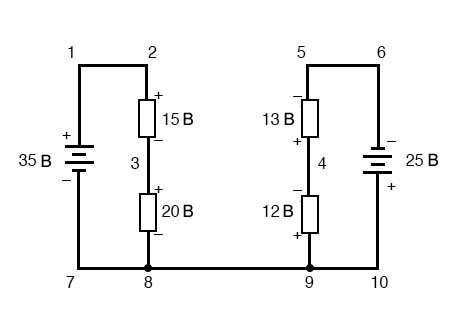
Набросок 10 – Правило напряжений Кирхгофа в сложной цепи
Дабы упростить задачку, я опустил значения сопротивлений и просто указал падение напряжения на каждом резисторе. Две последовательные цепи имеют между собой общий провод (провод 7-8-9-10), что делает вероятными измерения напряжения между этими 2-мя цепями. Если б мы желали найти напряжение между точками 4 и 3, мы могли бы составить уравнение правила напряжений Кирхгофа с напряжением между этими точками как неведомым:
E4-3 + 12 + 0 + 20 = 0
Набросок 11 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 4 и 3 Набросок 12 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 9 и 4 Набросок 13 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 8 и 9 Набросок 14 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 3 и 8
Обойдя контур 3-4-9-8-3, мы записываем значения падений напряжения так, как их регистрировал бы цифровой вольтметр, измеряя с красным измерительным проводом в точке впереди и черным измерительным проводом на точке сзади, когда мы продвигаемся вперед по контуру. Поэтому, напряжение в точке 9 относительно точки 4 является положительным (+) 12 вольт, так как «красный провод» находится в точке 9, а «черный провод» – в точке 4.
Напряжение в точке 3 относительно точки 8 составляет положительные (+) 20 вольт, так как «красный провод» находится в точке 3, а «черный провод» – в точке 8. Напряжение в точке 8 относительно точки 9, естественно, равно нулю, так как эти две точки электрически общие.
Наш окончательный ответ для напряжения в точке 4 относительно точки 3 – это отрицательные (-) 32 вольта, говорящие нам, что точка 3 по сути положительна относительно точки 4, конкретно это цифровой вольтметр показал бы при красном проводе в точке 4 и черном проводе в точке 3:
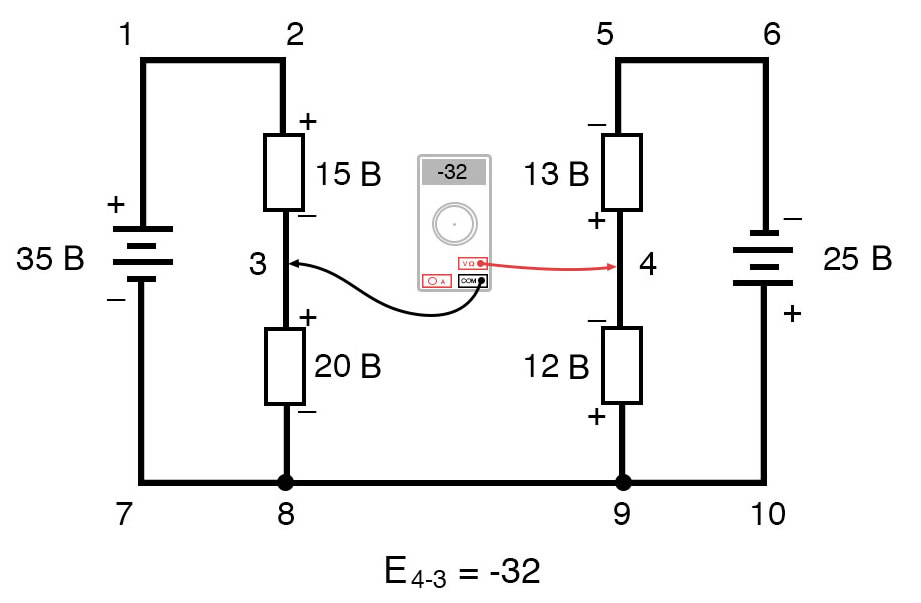
Набросок 15 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 4 и 3
Другими словами, первоначальное размещение наших «измерительных щупов» в этой задачке правила напряжений Кирхгофа было «оборотным». Если б мы сформировали наше уравнение второго закона Кирхгофа, начиная с E3-4, заместо E4-3, обходя тот же контур с обратной ориентацией измерительных проводов, окончательный ответ был бы E3-4 = +32 вольта:
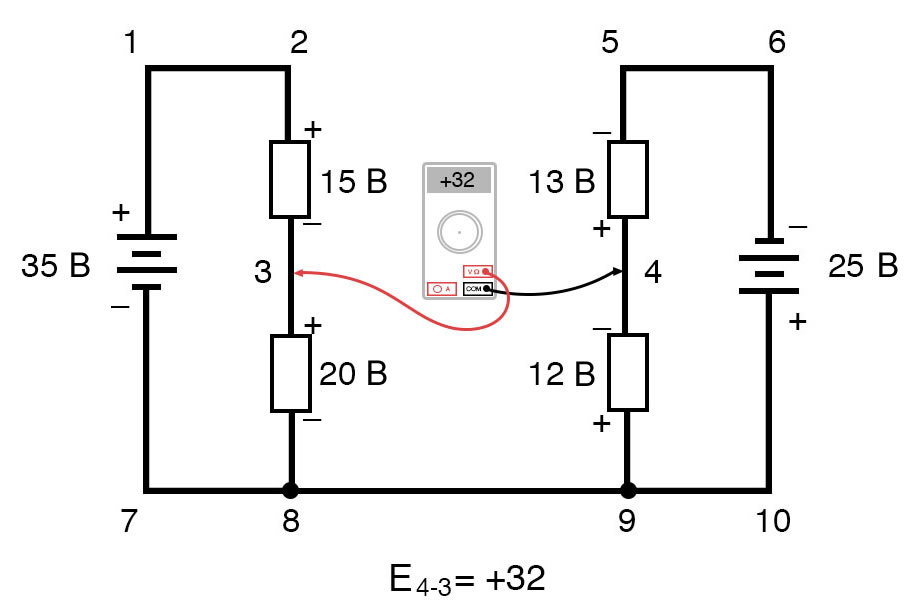
Набросок 16 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 3 и 4
Принципиально осознавать, что ни один из подходов не является «неверным». В обоих случаях мы приходим к правильной оценке напряжения между 2-мя точками 3 и 4: точка 3 положительна по отношению к точке 4, а напряжение между ними составляет 32 вольта.