Неофицальный веб-сайт кружка радиоэлектроники Клайпедского MSC
Warning: "continue" targeting switch is equivalent to "break". Did you mean to use "continue 2"? in /home/radijo/domains/radijo.eu/public_html/templates/radijotemv3/functions.php on line 199
Закон Ома
— пожалуй самый более применяемый закон в электронике.
Многих начанаяющих отпугивает его строгая книжная формулировка, за которой кроется простота его использования.
Закон Ома говорит: величина тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и назад пропорциональна его сопротивлению:
U = I x R ; R = U / I ; I = U / R ;
где I — это ток в цепи, измеряется в Амперах
U — это напряжение, измеряется в Вольтах
R — это сопротивление, измеряется в Омах
Данная формула очень ординарна, дабы было проще её уяснить, вы сможете нарисовать для себя на лююбом листке бумаги треугольник, котрый вы видите ниже. Это волшебный треугольник закона Ома — закрыв величину, которую для вас нужно отыскать, на оставшейся части треугольника вы увидите нужную для вас формулу.
к примеру, мы знаем рабочий ток и напряжение лампы (на лампочках для фонариков они указываются прямо на цоколе). Как отыскать сопротивление нити накаливания этой лампы? Все очень просто, закрываем сопротивление в треугольнике и лицезреем, что остается напряжение деленное на ток:
Источник тока 6.3 В (Вольта) (Аккамулятор)
Лампа на 6.3 Вольта, 100 мА (мили Ампер)
Согластно формуле получаем ответ: 6.3/100 = 0.63 Верблюда.
Лирическое отступление 1:
Почему верблюды? Да так как Вольты необходимо разделять на амперы, а мили Волты разделять на мили амперы, а микро Вольты делать на микро Амперы. При несоблюдении данного условия результат у нас будет выражен верюлюдами и кол-вом съеденных вашей бабушкой яблок, на её шестнадцатилетие.
Ну итак вот, создадим верно – 6.3 В / 0.1 А,если кому понравится 6300 мВ делим на 100 мА – должен получится разыскиваемый итог. А ежли уж и совершенно невтерпёж всё это можно перевести микро Вольты и микро Амперы.
Лирическое отступление 2:
Для любознательных мозгов будет нелишним знать, что приобретенный итог будет верен для работающей (включенной) лампочки. Сопротивление же холодной нити накала будет еще меньше.
Лирическое отступление 3:
Кстати лампы накаливания время от времени применяются как стабилизаторы тока.
Дабы лучше осознать слова напряжение, сопротивление приведу пример:
Представим насос, у которого есть вход и выход для воды – пусть это будет у нас источником тока с производительностью 12 л. воды. Извиняюсь – 12 Вольт. Дальше трубой соединяем вход с выходом помпы и заливаем в систему воду. Итак, мы получаем самую ординарную гидравлическую систему. Когда насос включен, вода начинает циркулировать по кругу, чем больше мы даем мощности насосу, тем резвее эта вода циркулирует. Итак вот в этом случае скорость воды на определенном участке — это ток, а толщина трубы, от которой зависит сколько воды пройдет через её сечение это сопротивление цепи, а напряжение это количество этой воды во всей системе, являющееся по собственной сущности мощностью насоса, выраженной в литрах на отрезок времени.
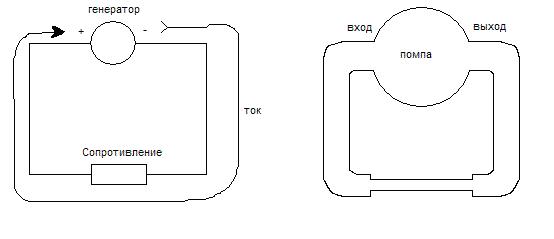
Данный пример я привел в качестве показательного и все свойства цепи нельзя представить в виде воды и помпы.
Сейчас есть такое понятие как мощность, P — данная величина охарактеризовывает количественный показатель выполняемой работы так сказать. P = U x I ; P = I 2 x R , тоесть ток в квадрате.
А сейчас давайте разберемся, что все-таки это все-же значат все эти примудрости в обычный форумуле, а конкретно, два сложных для осознания выражения: прямо пропорциональна и назад пропорциональна.
Что все-таки означает «величина тока прямо пропорциональна напряжению»? А это означает, что при увеличении напряжения цепи, возрастает и сила тока. Другими словами, чем больше напряжение, тем больше ток. Всё это справедливо для участка цепи при неменяющимся напряжении.
Что касается «обратно пропорциональна его сопротивлению», то тут все напротив. Чем больше сопротивление цепи, тем меньше в ней ток. Это справедливо при неизменяющимся сопротивлении.
Рассматривая этот закон применительно к фонарику с лампой накаливания и 3-мя круглыми батарейками начертаем схему:
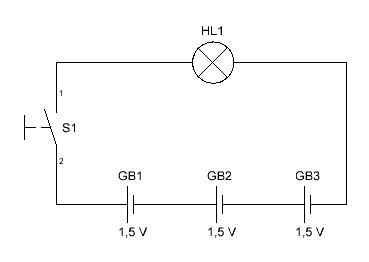
Электрическая схема фонарикус-вульгарус (фонарик обычный):
GB 1 — GB 3 — источник тока (три батарейки)
S 1 — выключатель
Согластно закону Ома: величина тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и назад пропорциональна его сопротивлению. Разглядим участок цепи, состоящий их лампочки.
Сейчас обычный вопрос: от чего зависит яркость лампочки? Верно — от силы тока, проходящего через нить накаливания этой лампочки. Другими словами яркость свечения лампочки мы можем применять как приятный показатель силы тока в цепи фонарика.
И вправду, какова будет яркость лампочки если поменять одну батарейку перемычкой?
«Естественно. она будет пылать тусклее!» — скажите Вы и будете правы. Вот фактически это и есть демонстрация фразы: «величина тока на участке цепи прямо пропорциональна напряжению». Чем больше батареек мы подключим (другими словами чем большее напряжение приложим) к одной лампочке, тем ярче она будет пылать ( и тем больший ток по ней протекает).
Закон Ома
В современном мире электронная техника развивается семимильными шагами. Каждый денек возникает что-то новое, и это не только лишь маленькие улучшения уже имеющихся моделей, но и результаты использования инноваторских технологий, позволяющих в разы сделать лучше свойства.
Не отстает от электронной техники и приборостроительная ветвь – ведь дабы создать и выпустить на рынок новые устройства, их нужно кропотливо протестировать, как на шаге проектирования и разработки, так и на шаге производства. Возникают новенькая измерительная техника и новые способы измерения, а, поэтому – новые определения и понятия.
Для тех, кто нередко сталкивается с непонятными сокращениями, аббревиатурами и определениями и желал бы поглубже осознавать их значения, и предназначена эта рубрика.
Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника либо электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году и назван в честь его первооткрывателя Георга Ома.
В собственной уникальной форме он был записан его создателем в виде : > (1)" />,
Тут X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая характеристики источника тока, неизменная в широких границах и независимая от величины тока, другими словами в современной терминологии электродвижущая сила (ЭДС) , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление наружной цепи R и, в конце концов, b параметр, характеризующий характеристики всей установки, в каком на данный момент можно усмотреть учёт внутреннего сопротивления источника тока r.
В таком случае в современных определениях, и в согласовании с предложенной создателем записью, формулировка Ома (1) выражает
Закон Ома для полной цепи:
>" />, (2)
Из закона Ома для полной цепи вытекают следствия:
- При r<<R сила тока в цепи назад пропорциональна её сопротивлению. А сам источник в ряде всевозможных случаев может быть назван источником напряжения
- При r>>R сила тока от параметров наружной цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.
(3)
(где есть напряжение либо падение напряжения либо, что то же, разность потенциалов между началом и концом участка проводника) тоже именуют «Законом Ома».
Таким макаром, электродвижущая сила в замкнутой цепи, по которой течёт ток в согласовании с (2) и (3) приравнивается:
= Ir + IR = U(r) + U (R) " /> (4)
Другими словами сумма падений напряжения на внутреннем сопротивлении источника тока и на наружной цепи равна ЭДС источника. Последний член в этом равенстве спецы именуют «напряжением на зажимах», так как конкретно его указывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.
К другой записи формулы (3), а конкретно:
," /> (5)
Применима другая формулировка:
Сила тока в участке цепи прямо пропорциональна напряжению и назад пропорциональна электрическому сопротивлению данного участка цепи.
Выражение (5) можно переписать в виде:
," /> (6)
где коэффициент пропорциональности G назван проводимость либо электропроводность. Вначале единицей измерения проводимости был «обратный Ом» — Mо, потом переименованный в Си́менс (обозначение: См, S).
Мнемоническая диаграмма для Закона
Схема, иллюстрирующая три составляющие закона Ома
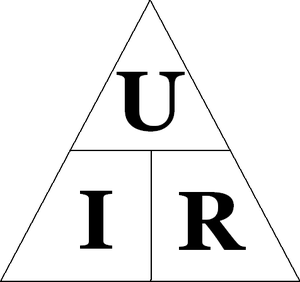
Диаграмма, помогающая уяснить закон Ома. Необходимо закрыть разыскиваемую величину, и два других знака дадут формулу для её вычисления
В согласовании с этой диаграммой формально может быть записано выражение:
," /> (7)
Которое всего только позволяет вычислить (применительно к известному току, создающему на данном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и назад пропорционально пропускаемому через него току, на физическом уровне неверно.
В специально оговорённых случаях сопротивление может зависеть от этих величин, но по дефлоту оно определяется только физическими и геометрическими параметрами проводника:
," /> (8)
Закон Ома и ЛЭП
Одним из важных требований к линиям электропередачи (ЛЭП) является уменьшение утрат при доставке энергии потребителю. Эти утраты в текущее время заключаются в нагреве проводов, другими словами переходе энергии тока в термическую энергию, за что трепетно омическое сопротивление проводов. Другими словами задачка заключается в том, дабы довести до потребителя как можно более значительную часть мощности источника тока = " /> при малых потерях мощности в полосы передачи = , где , причём сейчас есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления полосы передач).
В таком случае утраты мощности будут определяться выражением:
= ^2 r>\over^2 " /> (9)
Отсюда следует, что при неизменной передаваемой мощности её утраты вырастают прямо пропорционально длине ЛЭП и назад пропорционально квадрату ЭДС. Таким макаром лучше всемерное её повышение, что ограничивается электрической прочностью обмотки генератора. И увеличивать напряжение на входе полосы следует уже после выхода тока из генератора, что для неизменного тока является неувязкой. Но, для переменного тока эта задачка много проще решается при помощи применения трансформаторов, что и предназначило повсеместное распространение ЛЭП на переменном токе. Но при повышении напряжения в ней появляются утраты на коронирование и появляются трудности с обеспечением надёжности изоляции от земной поверхности. Потому наибольшее, фактически применяемое, напряжение в далеких ЛЭП не превосходит миллиона вольт.
Не считая того, хоть какой проводник, как показал Дж. Максвелл, при изменении силы тока в нём, испускает энергию в окружающее место, и поэтому ЛЭП ведёт себя как антенна, что принуждает в ряде всевозможных случаев вместе с омическими потерями брать в расчёт и утраты на излучение.
Закон Ома в дифференциальной форме
Сопротивление зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.
Полезно переписать закон Ома в так именуемой дифференциальной форме, в какой зависимость от геометрических размеров исчезает, тогда и закон Ома обрисовывает только электропроводящие характеристики материала. Для изотропных материалов имеем:
= \sigma \mathbf" />
Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В данном случае удельная проводимость является тензором ранга (1, 1).
Раздел физики, изучающий течение электрического тока в разных средах, именуется электродинамикой сплошных сред.
Закон Ома для переменного тока
Вышеприведённые суждения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит только учёт специфичных параметров потребителя, приводящих к разновремённости заслуги напряжением и током собственных наибольших значений, другими словами учёта фазового сдвига.
Если ток является синусоидальным с повторяющейся частотой , а цепь содержит не только лишь активные, но и реактивные составляющие (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся всеохватывающими:
= \mathbb \cdot Z," />
- U = U0eiωt — напряжение либо разность потенциалов,
- I — сила тока,
- Z = Re−iδ — всеохватывающее сопротивление (импеданс),
- R = (Ra2 + Rr2)1/2 — полное сопротивление,
- Rr = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),
- Rа — активное (омическое) сопротивление, не зависящее от частоты,
- δ = − arctg (Rr/Ra) — сдвиг фаз между напряжением и силой тока.
При всем этом переход от всеохватывающих переменных в значениях тока и напряжения к реальным (измеряемым) значениям может быть произведён взятием реальной либо надуманной части (но во всех элементах цепи одной и той же!) всеохватывающих значений этих величин. Соответственно, оборотный переход строится для, например, подбором таковой =U_0e^," /> что \mathbb = U. " /> Тогда все значения токов и напряжений в схеме нужно считать как \mathbb" />
Если ток меняется во времени, но не является синусоидальным (и даже повторяющимся), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать составляющие фурье-разложения тока действующими независимо.
Также стоит отметить, что закон Ома является только простым приближением для описания зависимости тока от разности потенциалов и от сопротивления и для некоторых структур справедлив только в узеньком спектре значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято дискуссировать вольт-амперную характеристику. Отличия от закона Ома наблюдаются также в случаях, когда скорость конфигурации электрического поля так велика, что нельзя третировать инерционностью носителей заряда.
Трактовка закона Ома
Закон Ома можно просто разъяснить с помощью теории Друде:
\cdot\tau> \cdot\vec E" />
3. Закон Ома
После проведения данного опыта Вы можете рассчитывать и определять ток, напряжение и сопротивление в электрической схеме для проверки закона Ома.
Нужные принадлежности
* Цифровой мультиметр
* Источник неизменного напряжения
* Резисторы — 1/4 Вт, 5%:
один резистор 470 Ом, один резистор 680 Ом, один резистор 2, 2 кОм, один резистор 4, 7 кОм.
ВВОДНАЯ ЧАСТЬ
По-видимому, более принципиальным главным принципом в электротехнике является закон Ома. Этот закон отражает связь, которая существует между током, напряжением и сопротивлением в электрической либо электронной цепи. Источник напряжения подключается к сопротивлению, что вызывает протекание через него тока. Величина тока определяется величиной приложенного напряжения и величиной сопротивления. Закон Ома утверждает, что на участке цепи ток прямо пропорционален напряжению и назад пропорционален сопротивлению. Эта связь выражается обычный формулой:
В данном выражении: I — ток в амперах, V — напряжение в вольтах, R — сопротивление в омах. Значение тока можно стремительно вычислить использовании калькулятора. К примеру, какой величины ток протекает через резистор 2, 2 кОм, присоединенный к источнику напряжения 6В? Ответ такой:
I = 6 В/2, 2 кОм = 6/2200 = 0, 00273 А
Это значение может быть выражено также в миллиамперах, другими словами, 2, 73 мА.
Как Вы понимаете, основная формула закона Ома может быть преобразована алгебраически, так что Вы можете определять либо напряжение, либо сопротивление. Этими другими формулами являются:
В. Вашей работе с электроникой Для вас часто придется применять закон Ома; Даже в самых сложных схемах Вы будете использовать это соотношение. Принципиально, дабы Вы могли проделывать такие расчеты при всех критериях.
Вычисления в согласовании с законом Ома
Для выполнения расчетов в согласовании с законом Ома Вы должны знать две величины из 3-х. Величины тока, напряжения и сопротивления
могут быть получены разными методами. Величины сопротивлении резисторов могут определяться по их цветовому коду либо фактическим измерением сопротивления резистора. Ток обычно определяется методом измерения. Величину напряжения нередко бывает просто найти, так как напряжение подается от источника питания, выходное напряжение которого фиксированно и понятно. К примеру, если применяется батарейка для карманного фонаря, то Вы понимаете, что ее напряжение составляет 1, 5 В. Все батареи частей имеют стандартные значения выходных напряжений, как и многие источники питания. Если напряжение непонятно, оно может быть, все же, измерено.
Короткое содержание
В данном опыте Вы будете собирать некоторые обыкновенные электрические схемы и делать электрические измерения, в итоге чего Вы можете проводить расчеты в согласовании с законом Ома. Для определенной схемы Вы научитесь делать расчет нужных величин. Потом Вы будете конструировать разные схемы и держать под контролем их величины методом измерении.
1. Обратитесь к схеме на рисунке 3-1. При узнаваемых значениях напряжения и сопротивления высчитайте величину протекающего в схеме тока. Запишите Ваше приобретенное значение в предусмотренное поле.
I = ______мА (вычисленное значение)
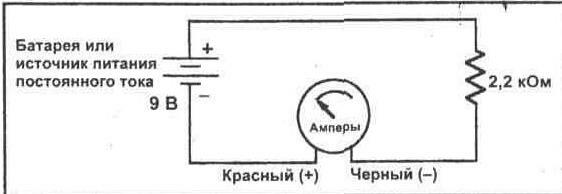
2. Соберите схему, показанную на рисунке 3-1. Используйте источник питания неизменного тока, настроенный таким макаром, дабы его выходное напряжение составляло 9 В. Для измерения тока в данной схеме Вы будете применять мультиметр. Установите предел измерения мультиметра на соответственное значение, которое основано на Ваших расчетах в шаге 1. Воткните красный испытательный вывод в гнездо А мультиметра.
3. После того, как Вы собрали схему, коснитесь черным пробником к отрицательному контакту батареи либо источника питания, а красным пробником прикоснитесь к неприсоединенному выводу резистора. Прочитайте показание величины тока на мультиметре. Запишите приобретенное значение.
I = ________мА (измеренное значение)
4. Сравните Ваше расчетное и измеренное значения. Растолкуйте причину различий, если таковые имеются.
5. Удвойте напряжение питания, обозначенное на рисунке 3-1. Какое сейчас новое напряжение питания схемы?
Напряжение питания = ______ вольт
6. Используя величину нового напряжения питания и прежнее сопротивление резистора, высчитайте величину нового тока.
/ = ______мА (вычисленное значение)
7. Определите новый ток, подсоединяя испытательные выводы мультиметра к схеме, как описано ранее.
I =______мА (измеренное значение)
8. Сравните величины токов в шагах 1 и 6 и в шагах 3 и 7. Как поменялась величина тока, когда поменялось напряжение питания? Согласуется ли такое изменение с законом Ома? Растолкуйте.
9. Демонтируйте схему, показанную на рисунке 3-1, и соберите схему, показанную на рисунке 3-2.
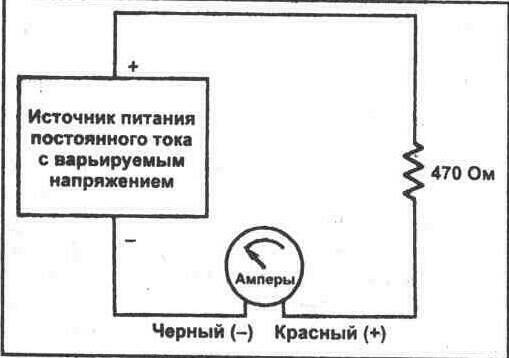
10. Определите величину тока, протекающего в схеме, используя функцию, описанную ранее. Запишите приобретенное значение.
I= ________мА (измеренное значение)
1. Используя значение измеренного Вами тока, высчитайте величину сопротивления резистора, применяя для этого закон Ома. Запишите величину сопротивления.
R = ______Ом (вычисленное значение)
12. Сейчас по цветовому коду резистора обусловьте его сопротивление и запишите отысканное значение. R = _________Ом (определенное по цветовому коду)
13. Сравните значение сопротивления, вычисленное с внедрением величины измеренного тока, с величиной сопротивления, определенной по цветовому коду. Растолкуйте хоть какой отличие.
14. Измените величину сопротивления резистора на 2, 2 кОм в схеме на рисунке 3-2.
15. Высчитайте величину ожидаемого тока. Запишите значение.
I =_______мА (вычисленное значение)
16. Определите величину тока, используя функцию, которая использовалась Вами в прошлых шагах.
I =_______мА (измеренное значение)
17. Сравните ток, который Вы измерили в шаге 16, с током, измеренным Вами в шаге 10. Как поменялся ток после конфигурации величины сопротивления резистора? Соответствуют л и приобретенные Вами результаты закону Ома? Растолкуйте.
18. Используйте источник питания неизменного тока с варьируемым напряжением, который Вы применяли в схеме на рисунке 3-2, и резистор 2, 2 кОм. Изменяйте напряжение от 0 до 12 В шагами (дискретами) по 2 В. Мерьте ток при каждом установленном напряжении.
19. Повторите шаг 18, используя резистор 4700м. Используя данные в шагах 18 и 19, построите графики тока зависимо от напряжения на миллиметровой бумаге.
ОБЗОРНЫЕ ВОПРОСЫ
1. К резистору 39 кОм был подключен источник питания с неведомым напряжением. Вы измерили ток и получили величину 0, 31 мА. Приложенное напряжение должно быть порядка:
2. Уменьшение напряжения, приложенного к резистору, приводит к:
а) повышению тока,
б) уменьшению тока,
в) сохранению той же величины тока,
г) падению величины тока до нуля.
3. Уменьшение сопротивления резистора, соединенного с источником питания, приводит к:
а) повышению тока,
б) уменьшению тока,
в) сохранению той же величины тока,
г) падению величины тока до нуля.
4. Смотрите Ваш график, приобретенный в шаге 19. Скорость конфигурации тока по отношению к изменению напряжения:
а) больше при наименьшей величине резистора,
б) больше при большей величине резистора,
в) меньше при наименьшей величине резистора,
г) та же при хоть какой величине резистора.
5. Для измерения тока с помощью мультиметра как он должен быть подключен к схеме?






