Пожалуй, закон Ома для участка цепи является основой электротехники и электроники. Хоть какое Пособие по физике для поступающих в университеты обрисовывает Закон Ома и хоть какой инженер должен его знать. Этот закон так прост, что его, по идее, должен знать и осознавать каждый школьник. Но я встречал людей с высшим техническим образованием, которые не знали как высчитать простейшую электрическую цепь из 2-ух резисторов. И это не шуточка. Вот поэтому я решил написать маленькую статью, посвящённую Закону Ома для участка цепи. Постараюсь выполнить это понятными словами.
Закон Ома для участка цепи определяет зависимость между силой тока в проводнике и напряжением (разностью потенциалов) между 2-мя точками этого проводника. Эти точки ещё именуют сечениями. Почему? Проводник, каким бы он ни был (круглым, квадратным либо хоть какой другой формы) можно на уровне мыслей рассечь (см. рис. 1). Это и будет сечение. А ещё есть понятие площадь поперечного сечения (обычно, когда молвят «сечение» по отношению к проводнику, то как раз и предполагают площадь поперечного сечения, но это уже другая тема).
Рис. 1. Сечение проводника.
В 1826 г. германским учёным Георгом Омом (1787-1854) было увидено, что отношение разности потенциалов (напряжения) на концах железного проводника к силе тока является величиной неизменной, другими словами: Данная величина находится в зависимости от геометрических параметров проводника (другими словами от его размеров, а именно, от площади поперечного сечения), также от его электрических параметров и температуры. Данная величина именуется омическим (активным) сопротивлением, либо просто сопротивлением.
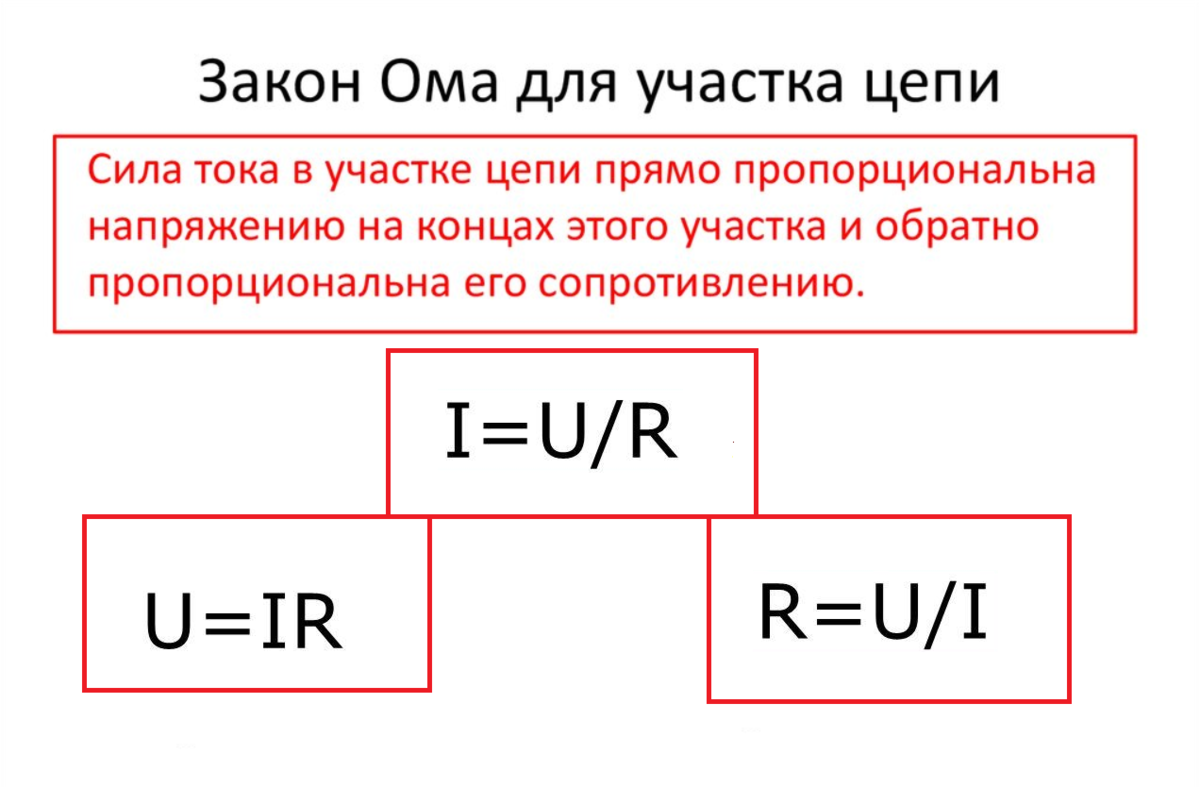
Определение закона Ома для участка цепи следующее
| Сила тока прямо пропорциональна разности потенциалов (напряжению) на концах участка цепи и назад пропорциональна сопротивлению этого участка: Где U – напряжение на данном участке цепи R – сопротивление данного участка цепи |
Омическое сопротивление проводника
Сопротивление проводника – это основная электрическая черта проводника. Эта черта определяет упорядоченное перемещение носителей тока в этом проводнике (либо на участке цепи).
Единица измерения омического сопротивления в СИ – ом (Ом). Проводник имеет сопротивление 1 Ом, если при силе тока в этом проводнике 1 А разность потенциалов (напряжение) на его концах равна 1 В, другими словами Другими словами, если взять проводник, по которому течёт ток силой 1 А, отмерить отрезок этого проводника таким макаром, дабы напряжение на концах этого отрезка было равно 1 В, то сопротивление этого отрезка будет 1 Ом (рис. 2).
Рис. 2. Сопротивление проводника.
Незначительно практики
Как говаривал один узнаваемый товарищ – теория без практики мертва. Надеюсь, что всё прочитанное выше вы сообразили. Но остался один вопрос – для чего это нужно? Где можно применить приобретенные познания на практике? Приведу два обычных примера, которые, но, применяются очень нередко в электронике.
Делитель напряжения
Достаточно нередко приходится сталкиваться с необходимостью снизить напряжение, к примеру, с 12 до 3 вольт. Выполнить это можно при помощи 2-ух резисторов (см. рис. 3). Если вы не понимаете, что такое резисторы, то советую ознакомиться со статьёй РЕЗИСТОРЫ. Ну а если понимаете, то далее сможете прочесть о том, как это выполнить.
Задачка, в общем-то, не непростая. Нужна подобрать два резистора таким макаром, дабы падение напряжения на одном из них составляло 3 вольта, а на втором – (12 – 3) = 9 вольт (для нашего примера). Не считая того, следует знать ток, который должен протекать в цепи. Допустим, что в нашем случае ток должен быть равен 50 мА (0,05 А). Тогда, используя закон Ома для участка цепи, вычислим полное сопротивление цепи, другими словами общее сопротивление резисторов R1 и R2: Напомню, что все единицы измерения должны соответствовать принятым в СИ, другими словами напряжение измеряется в ВОЛЬТАХ, ток – в АМПЕРАХ, а сопротивление – в ОМАХ.
Так как на любом участке цепи из последовательно включенных частей ток одинаков, то вычислить сопротивление резисторов R2 и R1 не составит труда: Ну вот и всё. Задачка решена. Но применять таковой делитель необходимо с мозгом. Ведь неважно какая нагрузка имеет своё сопротивление, которое именуется входным сопротивлением. Это означает, что, подключив нагрузку к выходу делителя, мы тем уменьшим сопротивление цепи, а это, в свою очередь, прирастит ток в цепи и падение напряжения на резисторе R1 возрастет, а на нагрузке, соответственно, уменьшится. Что из этого следует? А следует из этого тот грустный факт, что сколь-нибудь сильную нагрузку подключать к выходу делителя нецелесообразно. Потому такие делители применяются в главном, в электронных схемах, где протекают относительно маленькие токи.
Если любопытно, то вы сможете малость поэкспериментировать с делителем напряжения с помощью представленного ниже флэш-ролика (рис. 3). Для конфигурации входного напряжения и сопротивления резисторов воспользуйтесь соответствующыми "ползунками" либо конкретно введите данные в поля жёлтого цвета. Если флэш-ролик не отображается либо не работает, то для вас придётся настроить (либо поменять) ваш браузер и/либо установить (обновить) флэш-плеер.
Рис. 3. Делитель напряжения.
Как зажечь (но не спалить) светодиод?
Светодиоды в наше время используются очень обширно – от обычных устройств индикации до авто фонарей и светофоров. Может быть, у вас появлялась идея поменять лампочки в автомобиле на светодиоды. Как опытный автомобилист я для вас этого делать не советую – возни много, а смысла не достаточно. А ах так электронщик – помогу разобраться в премудростях включения светодиодов в электрическую цепь. Дело это несложное, но многие просто понятия не имеют, что и тут необходимо всё делать «по науке». А позже молвят, что светодиоды – вещь ненадёжная, хотя, обычно, выходят из строя светодиоды при правильной эксплуатации очень и очень изредка. А вот при неверной – ещё как. При желании спалить светодиод можно мгновенно.
Нужно сказать, что на данный момент в магазинах достаточно много различных «мигающих» и иных светодиодов, которые по сути являются электронными устройствами, встроенными в корпус светодиодов. Такие устройства можно подключать конкретно к источнику питания, без гасящего резистора. Но мы тут будем гласить об обыденных светодиодах.
Схема включения светодиода показана на рис. 4. При включении светодиода в цепь неизменного тока нужно соблюдать полярность (см. документацию на светодиод).
- Наибольшее напряжение
- Очень допустимый ток светодиода
Итак, допустим, что мы для чего-то желаем установить светодиод на автомобиль. Напряжение бортовой сети автомобиля при исправном оборудовании не может превосходить 15 В. На это напряжение и будем рассчитывать. Допустим, что наибольший ток нашего светодиода составляет 20 мА (0,02 А). Дальше нам нужно учитывать тот факт, что на любом полупроводнике (коим является и светодиод) падает какое-то напряжение. Для светодиодов это обычно 1,5…2 В. Примем его для нашего варианта равным 2 В.
Так как резистор и светодиод будут подключены последовательно, то очень вероятное напряжение на резисторе для нашего примера будет Где U1 – напряжение на гасящем резисторе R1 U – входное напряжение Ud – напряжение, падающее на светодиоде Сейчас остаётся высчитать резистор таким макаром, дабы через него протекал ток 20 мА при напряжении 13 В. Делаем это при помощи известного нам закона Ома для участка цепи: Ну вот и всё. Задачка решена – для включения светодиода с данными чертами нам будет нужно резистор сопротивлением 650 Ом. Но сопротивление – это не единственный параметр резистора. Резистор ещё обязан иметь подходящую мощность. Не считая того, индустрией не выпускаются резисторы сопротивлением 650 Ом (поточнее, выпускаются, но для особенных случаев). Но это уже другая история. Желаете знать больше? Читайте статью РЕЗИСТОРЫ.
Ну и не считая того предоставлю для вас возможность закрепить приобретенный материал при помощи флэш-ролика (рис. 4).
Закон Ома
На рис. показана схема знакомой для вас простейшей электронной цепи. Эта замкнутая цепь состоит из 3-х частей: источника напряжения – батареи GB, потребителя тока – нагрузки R, которой может быть, например, нить накала электронной лампы или резистор, и проводников, соединяющих источник напряжения с нагрузкой. Меж другим, если эту цепь дополнить выключателем, то получится полная схема карманного электронного фонаря.
Меж другим, если эту цепь дополнить выключателем, то получится полная схема карманного электронного фонаря.
| Обычная электронная цепь постоянного тока. |
Нагрузка R, владеющая определенным сопротивлением, является участком цепи. Значение тока на этом участке цепи зависит от действующего на нем напряжения и его сопротивления: чем больше напряжение и меньше сопротивление, тем не малым ток будет идти по участку цепи. Эта зависимость тока от напряжения и сопротивления выражается последующей формулой:
I = U/R,
где I – ток, выраженный в амперах, А; U – напряжение в вольтах, В; R – сопротивление в омах, Ом. Читается это математическое выражение так: ток на участке цепи прямо пропорционален напряжению на нем и вспять пропорционален его сопротивлению. Это основной закон электротехники, именуемый законом Ома (по фамилии Г. Ома), для участка электронной цепи. Используя закон Ома, можно по двум известным электронным величинам узнать неизвестную третью. Вот несколько примеров практического внедрения закона Ома.
1-ый пример: На участке цепи, обладающем сопротивлением 5 Ом, действует напряжение 25 В. Необходимо узнать значение тока на этом участке цепи.
Решение: I = U/R = 25 / 5 = 5 А.
2-ой пример: На участке цепи действует напряжение 12 В, создавая в нем ток, равный 20 мА. Каково сопротивление этого участка цепи? Поначалу ток 20 мА нужно выразить в амперах. Это будет 0,02 А. Тогда R = 12 / 0,02 = 600 Ом.
3-ий пример: Через участок цепи сопротивлением 10 кОм течет ток 20 мА. Каково напряжение, действующее на этом участке цепи? Здесь, как и раньше примере, ток должен быть выражен в амперах (20 мА = 0,02 А), сопротивление в омах (10кОм = 10000Ом). Как видно, U = IR = 0,02 х 10000 = 200 В. На цоколе лампы накаливания плоского карманного фонаря выштамповано: 0,28 А и 3,5 В. О чем молвят эти сведения? О том, что лампочка будет нормально светиться при токе 0,28 А, который обусловливается напряжением 3,5 В, Пользуясь законом Ома, нетрудно подсчитать, что накаленная нить лампочки имеет сопротивление R = 3,5 / 0,28 = 12,5 Ом. Это, подчеркиваю, сопротивление накаленной нити лампочки. А сопротивление остывшей нити значительно меньше. Закон Ома справедлив не только для участка, ну и для всей электронной цепи. В этом случае в значение R подставляется суммарное сопротивление всех частей цепи, в том числе и внутреннее сопротивление источника тока. Но при обычных расчетах цепей обычно пренебрегают сопротивлением соединительных проводников и внутренним сопротивлением источника тока.
В связи с этим приведу очередной пример: Напряжение электроосветительной сети 220 В. Какой ток потечет в цепи, если сопротивление нагрузки равно 1000Ом? Решение: I = U/R = 220 / 1000 = 0,22 А. Примерно такой ток потребляет электронный паяльник.
Всеми этими формулами, вытекающими из закона Ома, можно пользоваться и для расчета цепей переменного тока, но при условии, если в цепях нет катушек индуктивности и конденсаторов.
Закон Ома и производные от него расчетные формулы, достаточно легко уяснить, если пользоваться вот этой графической схемой, т. н. треугольник закона Ома:
Пользоваться этим треугольником просто, достаточно правильно уяснить, что горизонтальная линия в треугольнике означает знак деления (по аналогии дробной черты), а вертикальная линия в треугольнике означает знак умножения.
На данный момент рассмотрим такой вопрос: как влияет на ток резистор, включаемый в цепь попеременно с нагрузкой или параллельно ей? Разберем такой пример. У нас имеется лампочка от круглого электронного, фонаря, рассчитанная на напряжение 2,5 В и ток 0,075 А. Можно ли питать эту лампочку от батареи 3336Л, изначальное напряжение которой 4,5 В? Нетрудно подсчитать, что накаленная нить этой лампочки имеет сопротивление немногим больше 30 Ом. Если же питать ее от свежей батареи 3336Л, то через нить накала лампочки, по закону Ома, пойдет ток, фактически вдвое превосходящий тот ток, на который она рассчитана. Такой перегрузки нить не выдержит, она перекалится и разрушится. Но эту лампочку все же можно питать от батареи 336Л, если попеременно в цепь включить дополнительный резистор сопротивлением 25 Ом, как это показано на рис..
| Дополнительный резистор, включенный в цепь, ограничивает ток в этой цепи. |
В этом случае общее сопротивление внешней цепи будет равно примерно 55 Ом, т.е. 30 Ом – сопротивление нити лампочки Н плюс 25 Ом – сопротивление дополнительного резистора R. В цепи, Как видно, потечет ток, равный примерно 0,08 А, т.е. фактически такой же, на который рассчитана нить накала лампочки. Эту лампочку можно питать от батареи и с более высоким напряжением и даже от электроосветительной сети, если подобрать резистор соответствующего сопротивления. В этом примере дополнительный резистор ограничивает ток в цепи до подходящего нам значения. Чем больше будет его сопротивление, тем меньше будет и ток в цепи. В данном случае в цепь было включено попеременно два сопротивления: сопротивление нити лампочки и сопротивление резистора. А при поочередном соединении сопротивлений ток идентичен во всех точках цепи. Можно включать амперметр в всякую точку цепи, и всюду он будет показывать одно значение. Это явление можно сравнить с потоком воды в реке. Русло реки на различных участках может быть широким или узким, глубочайшим или небольшим. Но за определенный просвет времени через поперечное сечение хоть какого участка русла реки всегда проходит неразнообразное количество воды.
Дополнительный резистор, включаемый в цепь попеременно с нагрузкой (как, например, на рис. выше), можно рассматривать как резистор, «гасящий» часть напряжения, действующего в цепи. Напряжение, которое гасится дополнительным резистором или, как молвят, падает на нем, будет тем большущим, чем больше сопротивление этого резистора. Зная ток и сопротивление дополнительного резистора, падение напряжения на нем просто подсчитать все по той же знакомой для вас формуле U = IR, Здесь U – падение напряжения, В; I – ток в цепи, A; R – сопротивление дополнительного резистора, Ом. Применительно к нашему примеру резистор R ( на рис.) погасил избыток напряжения: U = IR = 0,08 х 25 = 2 В. Остальное напряжение батареи, равное приблизительно 2,5 В, упало на нити лампочки. Необходимое сопротивление резистора можно найти по другой знакомой для вас формуле R = U/I, где R – разыскиваемое сопротивление дополнительного резистора, Ом; U-напряжение, которое необходимо погасить, В; I – ток в цепи, А. Для нашего примера сопротивление дополнительного резистора равно: R = U/I = 2/0,075, 27 Ом. Меняя сопротивление, можно уменьшать или увеличивать напряжение, которое падает на дополнительном резисторе, и таким образом регулировать ток в цепи. Но дополнительный резистор R в такой цепи может быть переменным, т.е. резистором, сопротивление которого можно изменять (см. рис. ниже).
| Регулирование тока в цепи с помощью переменного резистора. |
В этом случае с помощью движка резистора можно плавно изменять напряжение, подводимое к нагрузке Н, а значит, плавно регулировать ток, протекающий через эту нагрузку. Включенный таким образом переменный резистор называют реостатом, С помощью реостатов регулируют токи в цепях приемников, телевизоров и усилителей. Во многих кинотеатрах реостаты использовали для плавного гашения света в зрительном зале. Есть, но, и другой способ подключения нагрузки к источнику тока с излишним напряжением – тоже с помощью переменного резистора, но включенного потенциометром, т.е. делителем напряжения, как показано на рис..
| Регулирование напряжения на нагрузке R2 с помощью переменного резистора включенного в электронную цепь потенциометром. |
Здесь R1 – резистор, включенный потенциометром, a R2 – нагрузка, которой может быть та же лампочка накаливания или какой – то другой устройство. На резисторе R1 происходит падение напряжения источника тока, которое частично или полностью может быть подано к нагрузке R2. Когда движок резистора находится в последнем нижнем положении, к нагрузке напряжение вообще не подается (если это лампочка, она пылать не будет). По мере перемещения движка резистора ввысь мы будем подавать все большее напряжение к нагрузке R2 (если это лампочка, ее нить будет накаливаться). Когда же движок резистора R1 окажется в последнем верхнем положении, к нагрузке R2 будет подано все напряжение источника тока (если R2 – лампочка карманного фонаря, а напряжение источника тока большущее, нить лампочки перегорит). Можно опытным способом найти такое положение движка переменного резистора, при котором к нагрузке будет подано необходимое ей напряжение. Переменные резисторы, включаемые потенциометрами, широко употребляют для регулирования громкости в приемниках и усилителях. Резистор может быть непосредственно подключен параллельно нагрузке. В таком случае ток на этом участке цепи разветвляется и идет 2-мя параллельными методами: через дополнительный резистор и основную нагрузку. Больший ток будет в ветки с наименьшим сопротивлением. Сумма же токов обеих ветвей будет равна току, применяемому на питание внешней цепи. К параллельному соединению прибегают в тех cлучаях, когда необходимо ограничить ток не во всей цепи, как при поочередном включении дополнительного резистора, а только на каком – то участке. Дополнительные резисторы подключают, например, параллельно миллиамперметрам, чтобы ими можно было определять большие токи. Такие резисторы именуют шунтирующими либо шунтами. Слово шунт значит ответвление.